基于Infogram的共振解调方法在滚动轴承故障特征提取中的应用

夏均忠， 于明奇， 黄 财， 汪治安， 吕麒鹏

(1.军事交通学院 军用车辆工程技术研究中心，天津 300161；2.东莞市TR轴承有限公司，广东 东莞 523000)

滚动轴承广泛用于旋转机械中，其运行状态是否正常往往直接影响整台设备的性能，因此对滚动轴承技术状态监测和早期故障诊断具有重要意义。滚动轴承通常由内圈、外圈、滚动体和保持架组成，当其中某一部分表面发生局部故障时，产生的脉冲会激起轴承及其相邻部件的共振，产生调制现象[1]。

共振解调利用故障产生的频率信号与系统本身固有的振荡频率相同时会产生共振的原理，通过放大和分离故障特征信号，可以比较准确地判断早期微弱故障的严重程度和损伤部位。利用共振解调从复杂的振动信号中提取脉冲响应特征是广为采用的滚动轴承故障检测方法。然而传统的共振解调技术存在带通滤波器参数(中心频率和滤波带宽)需要预先人为确定，具有较大的偶然性和局限性等缺陷[2-3]。快速峭度图(Fast Kurtogram)方法提出以来常用于确定带通滤波器参数[4-6]，但寻求的特征频率过大、带宽过宽，导致其在信号信噪比较低、含有随机脉冲噪声或者故障脉冲重复率较大等情况下容易失效[7-10]。

Barszcz等[11]提出突起度图(Protrugram)方法，该方法基于窄带包络谱幅值的谱峭度指标，其应用效果优于快速峭度图，但未给出理论上的合理证明，且带宽需要预先确定[12-14]。Antoni[15]引入谱负熵(Spectral Negentropy)概念，提出信息图(Infogram)法，该方法同时考虑了信号脉冲性和循环平稳性，在含有随机脉冲噪声等情况下均取得了理想效果[16-17]。

1 信息图

故障脉冲的出现，意味着打破了系统正常时的状态平衡，系统熵值也会发生变化。定义信号频带上的熵值为谱熵(Spectral Entropy)。当轴承正常状态时，信号的能量波动为常量，谱熵值最大，反之，当故障脉冲引起能量波动变化时，谱熵值最小，这与峭度指标变化恰好相反。为使其具有与谱峭度相同的物理意义，取谱熵负值定义为谱负熵。

定义长度为L的离散时域信号x(n)(n=0, …,L)，其频带[f-Δf/2,f+Δf/2]上的平方包络SEx(n;f, Δf)

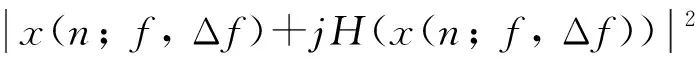
(1)

式中：H(·)为希尔伯特变换。时域中的谱负熵定义为

(2)

式中：〈·〉为均值运算。时域中的谱负熵可以看作是权重为ln(SEx(n;f,Δf)2/〈SEx(n;f,Δf)2〉)的谱峭度(Spectral Kurtosis，SK)。同SK作用相同，ΔIe(f;Δf)也可以用于表征频带[f-Δf/2,f+Δf/2]中因局部故障引起的脉冲特性。

除脉冲特性外，局部故障也表现出循环平稳特性，可用频域中的谱负熵ΔIE(f;Δf)度量

(3)

式中：SESx(α;f,Δf)为频带[f-Δf/2,f+Δf/2]上的平方包络谱

SESx(α;f,Δf)=F(SEx(n;f,Δf))

(4)

式中：F(·)为傅里叶变换；α为频率变化值；即循环频率。故障瞬态的存在使ΔIe(f;Δf)和ΔIE(f;Δf)均增大，但噪声等影响导致两者变化程度却不同，将两者加权平均，计算其平均谱负熵，同时度量脉冲性和循环平稳性更具有意义，表达式为

(5)

为便于表示和计算，时域中所有谱负熵值构成的信息图定义为平方包络信息图(Square Envelope Infogram，SE Infogram)。频域中所有谱负熵值构成的信息图定义为平方包络谱信息图(Square Envelope Spectrum Infogram，SES Infogram)。所有平均谱负熵值构成的信息图定义为平均信息图(Average Infogram)。

从上述分析可知，平均信息图集成了平方包络信息图和平方包络谱信息图的特点，更具有适应性。论文以轴承为研究对象，提出基于Inforgram的共振解调方法：利用平均信息图确定带通滤波器参数，从其滤波信号共振解调谱中提取轴承故障特征。

2 仿真分析

构造周期性振动脉冲仿真信号x(t)

(6)

式中：A(t)为瞬态幅值；δ(t)为随机噪声或脉冲噪声；θ(t)为谐波干扰或调制啮合干扰；q为瞬态脉冲数量；fc为故障特征频率。s(t)为周期性脉冲响应函数，表达式为

(7)

式中：bw，f0分别为最佳共振频带的带宽和中心频率。采样频率fs=50 kHz，采样时间为1 s。

2.1 脉冲噪声干扰仿真分析

根据式(6)和式(7)，设置参数如下，A(t)=1.3 mV(0≤t≤1)，fc=47 Hz，bw=860 Hz，f0=8.3 kHz。加入0.3sin(183πt)和0.2cos(27πt)两个谐波成分，在t=0.82 s处添加一个脉冲噪声(幅值2.5 mV，共振频率18.5 kHz，带宽490 Hz)，生成含有脉冲噪声的周期性振动脉冲信号，如图1(a)所示。添加高斯白噪声(信噪比SNR=-4 dB)，其加噪后仿真信号如图1(b)所示。

(a)脉冲噪声干扰仿真信号

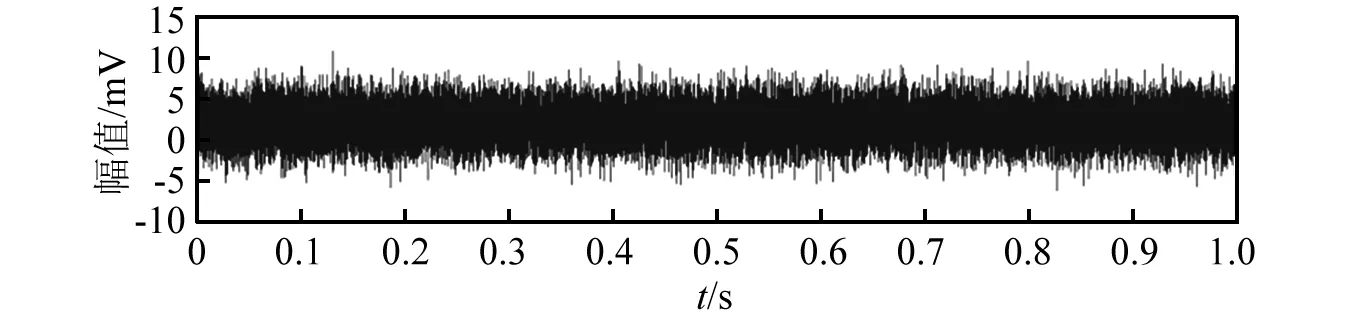
(b)加噪仿真信号图1 脉冲噪声干扰仿真信号时域波形Fig.1 Time domain waveform of the simulated signal with the impulsive noise

对加噪仿真信号分别进行快速峭度图和平均信息图计算，其结果如图2和图3所示。

由图3可知，使仿真信号平均谱负熵值最大的中心频率f0-a=8 203.16 Hz，频率分辨率带宽bw-a= 27Hz，其共振频带在初始设置的共振频带范围内。而受到脉冲噪声干扰，快速峭度图优选的共振频带(中心频率f0-f=18 229.17 Hz，带宽bw-f=1 047.67 Hz)偏离设置范围。

图2 脉冲噪声干扰仿真信号快速峭度图Fig.2 Fast kurtogram of the simulated signal with the impulsive noise

图3 脉冲噪声干扰仿真信号平均信息图Fig.3 Average Infogram of the simulated signal with the impulsive noise

用上述参数构建带通滤波器分别对该仿真信号进行带通滤波，并对其进行频谱分析，提取故障特征频率，得到滤波信号的共振解调谱，如图4所示。

图4(a)中频率成分嘈杂，并未发现故障特征频率(47 Hz)及其谐波。而由平均信息图确定的带通滤波器，其滤波信号的共振解调谱(见图4(b))中，故障特征频率(47.31 Hz)及其谐波清晰明显。

(a)应用快速峭度图优选共振频带

(b)应用平均信息图优选共振频带图4 脉冲噪声干扰仿真信号共振解调谱Fig.4 Resonance demodulation spectrum of the simulated signal with the impulsive noise

2.2 故障脉冲高重复率仿真分析

根据式(6)和式(7)，设置参数如下，A(t)=1.3 mV(0≤t≤1)，fc=87 Hz，bw=78 Hz，f0=8.3 kHz。添加0.3sin(183πt)和0.2cos(27πt)两个谐波成分，生成故障脉冲高重复率的周期性振动脉冲信号，如图5(a)所示。添加高斯白噪声(信噪比SNR=-4 dB)，其加噪仿真信号，如图5(b)所示。

(a)故障脉冲高重复率仿真信号

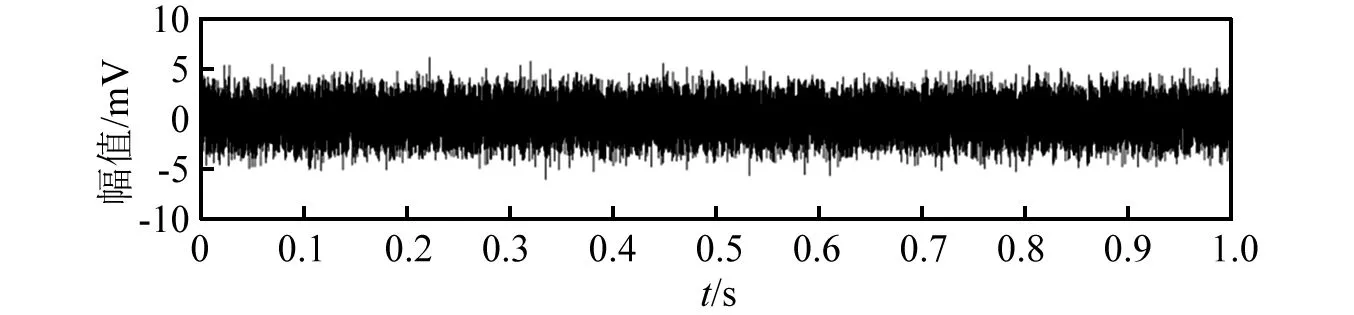
(b)加噪仿真信号图5 故障脉冲高重复率仿真信号时域波形Fig.5 Time domain waveform of simulated signal with high repetition rate

应用快速峭度图和平均信息图分别对加噪仿真信号的共振频带进行优选，其结果如图6和图7所示。

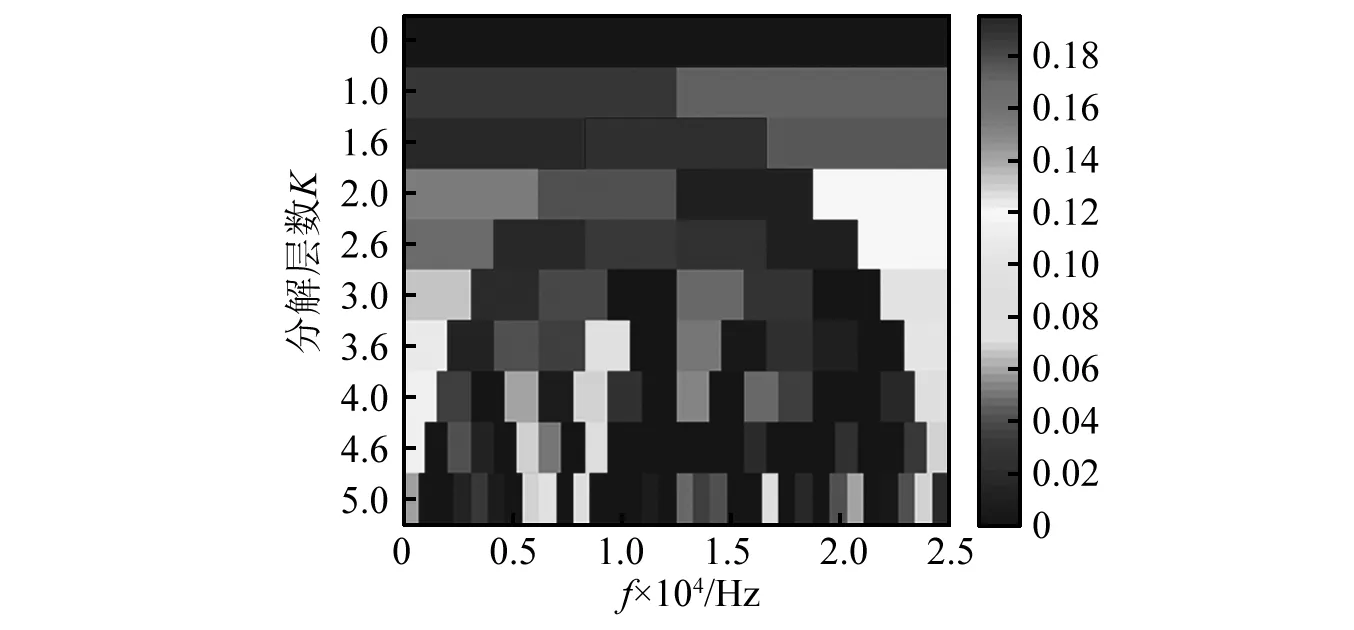
图6 故障脉冲高重复率仿真信号快速峭度图Fig.6 Fast kurtogram of the simulated signal with high repetition rate

图7 故障脉冲高重复率仿真信号平均信息图Fig.7 Average Infogram of the simulated signal with high repetition rate

由图6和图7可知，快速峭度图和平均信息图确定的中心频率分别为f0-f=4 166.67 Hz，f0-a=8 593.75 Hz，带宽分别为bw-f=8 333.33 Hz，bw-a=27Hz。显然快速峭度图找寻的带宽过宽，而平均信息图确定的共振频带更接近设置的共振频带。其滤波信号共振解调谱，如图8所示。

(a)应用快速峭度图优选共振频带

(b)应用平均信息图优选共振频带图8 故障脉冲高重复率仿真信号共振解调谱Fig.8 Resonance demodulation spectrum of the simulated signal with high repetition rate

从图8(a)未辨别出故障特征频率(87 Hz)及其谐波。从图8(b)可以清晰辨别出故障特征频率(86.99 Hz)及其谐波。

通过上述仿真分析可知，在脉冲噪声干扰等情况下，平均信息图对共振频带的优选效果要强于快速峭度图。

3 试验验证

试验装置由驱动电机、振动加速度传感器、扭矩解码/编码器、联轴器和功率计等组成，如图9所示[18]。试验轴承为SKF 6205-2RS深沟球轴承，支撑驱动电机驱动端，其技术参数见表1。

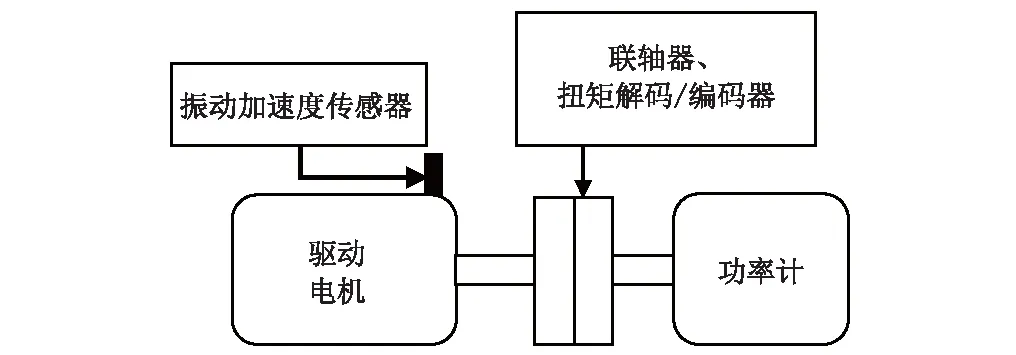
图9 实验装置示意图Fig.9 The schematic diagram of experimental device

滚动体直径d/mm节圆直径D/mm内径DI/mm外径Do/mm滚动体数Z接触角α/(°)839255290

使用电火花在轴承内圈、滚动体上加工直径均为0.36 mm(深度为0.28 mm)的圆坑，模拟内圈、滚动体点蚀故障。电机转速分别设定为1 750 r/min、1 797 r/min。采样频率为12 kHz，采样时间为1 s。

滚动轴承内圈故障、滚动体故障振动信号的时域波形及其频谱，如图10所示。由于背景噪声、调制因素等干扰，图中轴承振动信号的时域波形难以识别故障特征，且频谱图中出现高频共振成分。

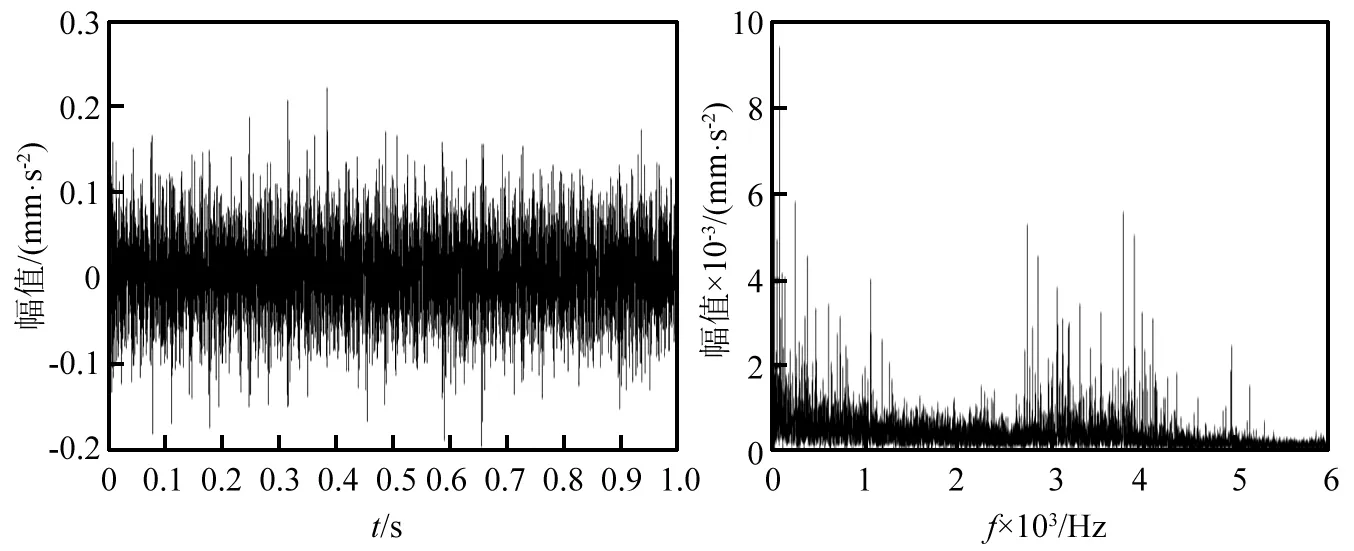
(a)内圈故障

(b)滚动体故障图10 故障轴承振动信号时域波形及其频谱Fig.10 Time domain waveform and spectrum of fault bearing vibration signal

对故障轴承振动信号进行平均信息图计算，其结果如图11所示。

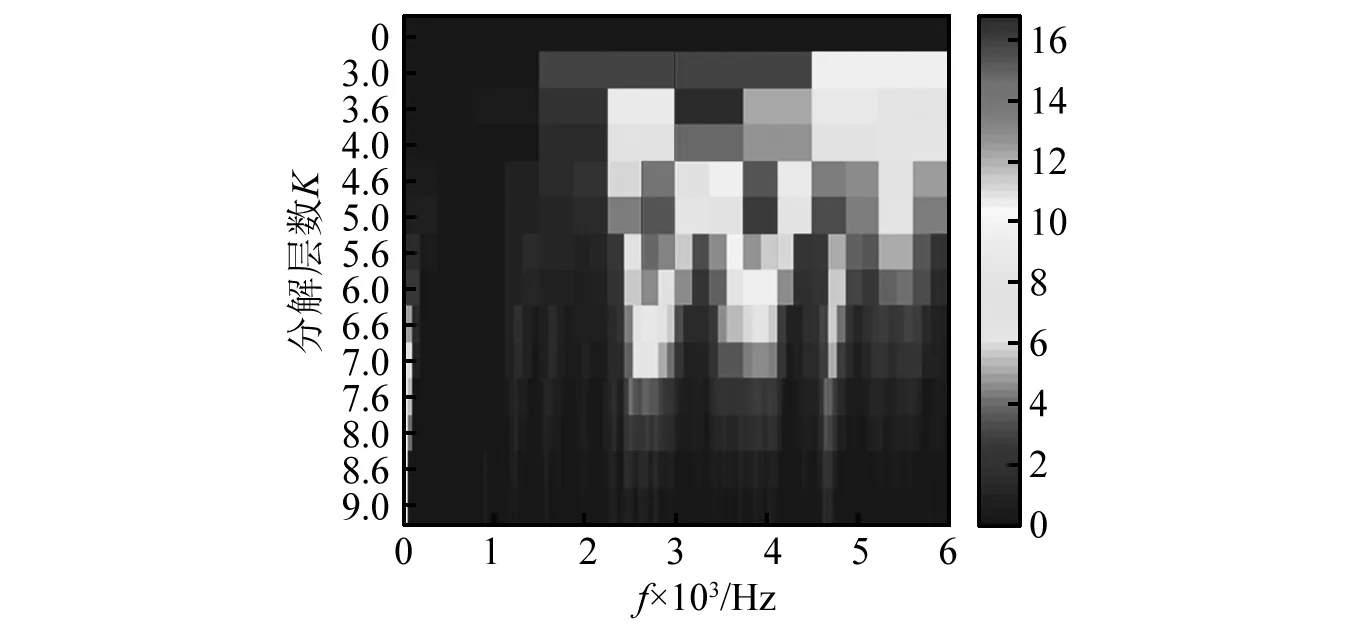
(a)内圈故障

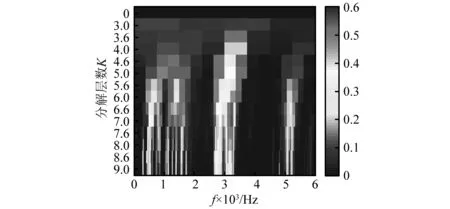
(b)滚动体故障图11 故障轴承振动信号平均信息图Fig.11 Average Infogram of fault bearing vibration signal

由图11(a)可知，内圈故障振动信号中，平均信息图所选取的共振频带中心频率f0-a=3 000 Hz，带宽bw-a=23.5Hz。而应用快速峭度图确定的中心频率f0-f=2 718.75 Hz，带宽bw-f=187.5 Hz。其滤波信号共振解调谱，如图12所示。

由图12可知，较之快速峭度图，平均信息图确定的共振频带，其共振解调谱中内圈故障特征频率fBPFI=158 Hz及其谐波更为突出，且边频带fB(128.8 Hz,187.2 Hz)、转频fr(29.21 Hz)及其谐波也清晰可见。

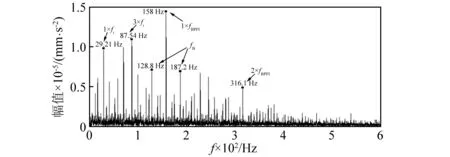
(a)应用平均信息图优选共振频带

(b)应用快速峭度图优选共振频带图12 轴承内圈故障振动信号共振解调谱Fig.12 Resonance demodulation spectrum of bearing vibration signal with inner race fault

由图11(b)可知，滚动体故障振动信号中，平均信息图所选取的滤波频带中心频率f0-a=562.5 Hz，带宽bw-a=28.5Hz。而应用快速峭度图确定的中心频率f0-f=3 125 Hz，带宽bw-f=250 Hz。其滤波信号共振解调谱，如图13所示。

(a)应用平均信息图优选共振频带

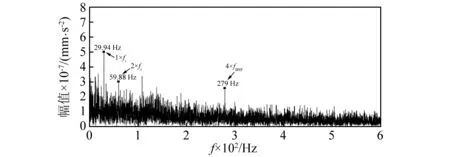
(b)应用快速峭度图优选共振频带图13 轴承滚动体故障振动信号共振解调谱Fig.13 Resonance demodulation spectrum of bearing vibration signal with ball fault

由图13(a)可清晰辨识滚动体故障特征信息：滚动体故障特征频率fBSF(71.87 Hz)及其谐波，保持架故障频率fFTF(11.81 Hz)和转频fr(29.76 Hz)。而图13(b)中只能辨识滚动体故障特征频率的四次谐波(279 Hz)和转频fr(29.76 Hz)。

通过轴承内圈、滚动体故障振动信号分析可知，与快速峭度图相比，由平均信息图确定的带通滤波器参数(中心频率和带宽)，其滤波信号的共振解调谱，有两个优势：①故障特征突出(见图12)；②包含故障信息较多(见图13)。

4 结 论

针对快速峭度图选取带通滤波器参数精度不高问题，论文提出了基于信息图的共振解调方法，并将其应用于滚动轴承故障特征提取。通过仿真信号和实测信号验证了该方法的有效性和优越性。

(1)解决了基于快速峭度图的共振解调方法在脉冲噪声干扰、故障脉冲高重复率等情况下容易失效的问题，其滤波信号的共振解调谱中故障特征明显，故障信息较为丰富。

(2)轴承内圈发生故障时，其信号共振解调谱中包含内圈故障特征频率fBPFI及其谐波，以转频fr为间隔分布在fBPFI两侧的边频带fB，fr及其谐波；轴承滚动体发生故障时，其信号共振解调谱中包含滚动体故障特征频率fBSF及其谐波，以保持架故障频率fFTF为间隔分布在fBSF两侧的边频带，fFTF及其谐波，fr及其谐波。

参 考 文 献

[ 1 ] 夏均忠，刘远宏，李树珉，等. 应用Hilbert变换和ZFFT提取变速器齿轮故障特征[J]. 振动与冲击， 2013， 32(6)： 63-66.

XIA Junzhong，LIU Yuanhong，LI Shumin，et al. Gearing fault detection using Hilbert transform and ZFFT[J]. Journal of Vibration and Shock, 2013, 32(6): 63-66.

[ 2 ] 周智，朱永生，张优云，等. 基于EEMD与共振解调的自适应故障诊断[J]. 振动与冲击， 2013， 32(2)： 76-80.

ZHOU Zhi， ZHU Yongsheng， ZHANG Youyun，et al. Adaptive fault diagnosis of rolling bearings based on EEMD and demodulated resonance[J]. Journal of Vibration and Shock, 2013, 32(2): 76-80.

[ 3 ] 张龙，熊国良，黄文艺. 复小波共振解调频带优化方法和新指标[J]. 机械工程学报， 2015， 51(3)： 129-138.

ZHANG Long，XIONG Guoliang，HUANG Wenyi. New procedure and index for the parameter optimization of complex wavelet based resonance demodulation [J]. Journal of Mechanical Engineering, 2015, 51(3): 129-138.

[ 4 ] ANTONI J. Fast computation of the Kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21(1): 108-124.

[ 5 ] 王宏超，陈进，董广明，等. 基于快速Kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J]. 振动与冲击， 2013， 32(1)： 35-38.

WANG Hongchao， CHEN Jin， DONG Guangming，et al. Application of resonance demodulation in rolling bearing fault feature extraction based on fast computation of Kurtogram[J]. Journal of Vibration and Shock, 2013, 32(1): 35-38.

[ 6 ] 张晓涛，唐力伟，王平，等. 基于SVD与Fast Kurtogram算法的滚动轴承声发射故障诊断[J]. 振动与冲击， 2014， 33(10)： 101-105.

ZHANG Xiaotao， TANG Liwei， WANG Ping， et al. Acoustic emission fault diagnosis of rolling bearings based SVD and Fast Kurtogram algorithm[J]. Journal of Vibration and Shock, 2014, 33(10): 101-105.

[ 7 ] LEI Y G，LIN J，HE Z J，et al.Application of an improved Kurtogram method for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1738-1749.

[ 8 ] GUO W，TSE P W，DJORDJEVICH A. Faulty bearing signal recovery from large noise using a hybrid method based on spectral kurtosis and ensemble empirical mode decomposition[J]. Measurement, 2012, 45(5): 1308-1322.

[ 9 ] 唐贵基， 王晓龙， 邓飞跃. 改进增强峭度图和增强包络谱在滚动轴承故障诊断上的应用[J]. 振动与冲击， 2014， 33(13)： 53-58.

TANG Guiji， WANG Xiaolong， DENG Feiyue. Application of improved enhanced Kurtogram and enhanced envelope spectrum in fault diagnosis of rolling bearings[J]. Journal of Vibration and Shock, 2014, 33(13): 53-58.

[10] 彭畅，柏林，刘小峰. 基于鲁棒性小波包峭度图的滚动轴承故障诊断[J]. 振动、测试与诊断， 2016， 36(1)： 11-16.

PENG Chang， BO Lin， LIU Xiaofeng. Robust wavelet transform-based Kurotgram for the fault diagnostics of rolling bearing element bearing[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(1): 11-16.

[11] BARSZCZ T，JABLONSKI A. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram[J]. Mechanical Systems and Signal Processing, 2011,25(1): 431-451.

[12] WANG D，TSE P W，TSUI K L. An enhanced Kurtogram method for fault diagnosis of rolling element bearings[J]. Mechanical Systems and Signal Processing, 2013, 35(1/2): 176-199.

[13] 代士超，郭瑜，伍星，等. 基于子频带谱峭度平均的快速谱峭度图算法改进 [J]. 振动与冲击， 2015， 34(7)： 98-102.

DAI Shichao， GUO Yu， WU Xing，et al. Improvement on fast Kurtogram algorithm basedon sub-frequency-band spectral kurtosis average[J]. Journal of Vibration and Shock, 2015, 34(7): 98-102.

[14] 马新娜，杨绍普. 典型谱峭图在共振解调方法中的应用[J]. 振动、测试与诊断， 2015， 35(6)： 1140-1144.

MA Xinna， YANG Shaopu. Study and application of demodulated resonance based on Typi-Kurtogram[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(6): 1140-1144.

[15] ANTONI J. The infogram: entropic evidence of the signature of repetitive transients[J]. Mechanical Systems and Signal Processing, 2016, 74:73-94.

[16] LI C，CABRERA D，CERRADA M，et al. Extracting repetitive transients for rotating machinery diagnosis using multiscale clustered grey infogram[J].Mechanical Systems and Signal Processing, 2016, 76/77: 157-173.

[17] WANG Dong. An extension of the infograms to novel Bayesian inference for bearing fault feature identification[J]. Mechanical Systems and Signal Processing , 2016, 80: 19-30.

[18] SMITH W A，RANDALL R B. Rolling element bearing diagnostics using the case western reserve university data：a benchmark study[J]. Mechanical Systems and Signal Processing, 2015, 64/65: 100-131.