新建时速400 km高速铁路32 m简支梁设计参数研究
2018-06-28班新林苏永华程泽农
班新林,苏永华,张 楠,程泽农
(1.中国铁道科学研究院 铁道建筑研究所,北京 100081;2.北京交通大学 土木建筑工程学院,北京 100044)
我国高速铁路运营里程已超过2.3万km,“四纵四横”高速铁路干线运输网络基本成型。中国居世界高铁里程榜首,已建成全世界规模最大、运营速度最高的高速铁路网,高速铁路运营里程约占世界高速铁路运营里程的50%以上。随着社会、经济和技术的发展,我国对于高速铁路建设的实际需求越来越大,并规划了“八纵八横”高速铁路干线网,同时存在发展时速400 km高速铁路的需求。国外高速铁路建设中,英国规划的HS2线,全长220.5 km,计划2017年开工,最初运行速度约为360 km/h(225英里/小时),预留未来运营速度约为400 km/h(250英里/小时)的潜力。俄罗斯莫斯科至喀山高铁,全长770 km,也提出了设计时速400 km的需求。因此,基于我国高速铁路常用跨度简支梁的建设情况,研究时速400 km高速铁路 32 m 简支梁的设计参数十分有必要。
1 设计参数
高速铁路桥梁区别于普速铁路桥梁的主要特征是须具有足够大的刚度。我国铁路桥梁设计规范中通过梁体挠跨比、梁端转角及梁体竖向基频等限值保证梁体具有必要的竖向刚度。同时还要保持列车高速运行的平顺性,主要指标是梁体残余徐变变形和工后基础不均匀沉降。现行规范对时速350 km高速铁路桥梁设计参数的主要规定如下[1-2]:
1)基频。对于运行车长24~26 m 动车组、跨度不大于32 m 的混凝土双线简支箱梁的情况,规范给出了不需进行动力检算的竖向自振频率限值。对于32 m梁(计算跨度31.5 m),竖向自振频率不应小于150/L(L为跨度),即4.76 Hz。
2)挠跨比。规范制定时,通过计算高速列车以各种速度通过不同跨度简支梁时的车桥耦合振动响应,获得各种计算工况下的车辆振动加速度、轮重减载率、脱轨系数、桥梁振幅等,研究梁体不同竖向刚度时车桥的振动状态,提出32 m简支梁在静活载作用下竖向挠跨比不应大于1/1 600。
3)梁端转角。对于采用无砟轨道的桥梁,由于梁端竖向转角使得梁缝两侧的钢轨支点分别产生钢轨上拔和下压现象。当上拔力大于钢轨扣件的扣压力时将导致钢轨与下垫板脱开,当垫板所受下压力过大时可能导致垫板破坏。为了保证梁端扣件系统的受力及线路安全,减少运营期间的维修工作量,规定32 m简支梁(梁端悬出长度0.55 m)在静活载作用下梁端转角限值为1.5‰ rad。
4)残余徐变变形。轨道铺设完成后,32 m无砟桥面预应力混凝土梁的竖向残余徐变变形不应大于10 mm。
5)工后基础不均匀沉降。高速铁路桥梁墩台基础的沉降应按恒载计算,无砟桥面的32 m简支梁在恒载作用下产生的工后基础不均匀沉降不应大于5 mm。
2 计算理论
以刚体动力学方法建立车辆模型,以有限元方法建立桥梁模型,假定轮轨之间密贴,以全过程迭代法求解车-桥动力耦合方程。分析中,车辆模型考虑6个自由度(见图1),其中车体2个自由度,每个转向架各2个自由度,一系悬挂中的刚度和阻尼的影响不体现在刚度矩阵和阻尼矩阵中,而是后续步骤中在总体刚度矩阵中添加转向架与桥面之间的垂向弹簧。质量矩阵方面,考虑轮对质量在竖向及扭转方向上对桥梁总体质量矩阵的影响[3]。
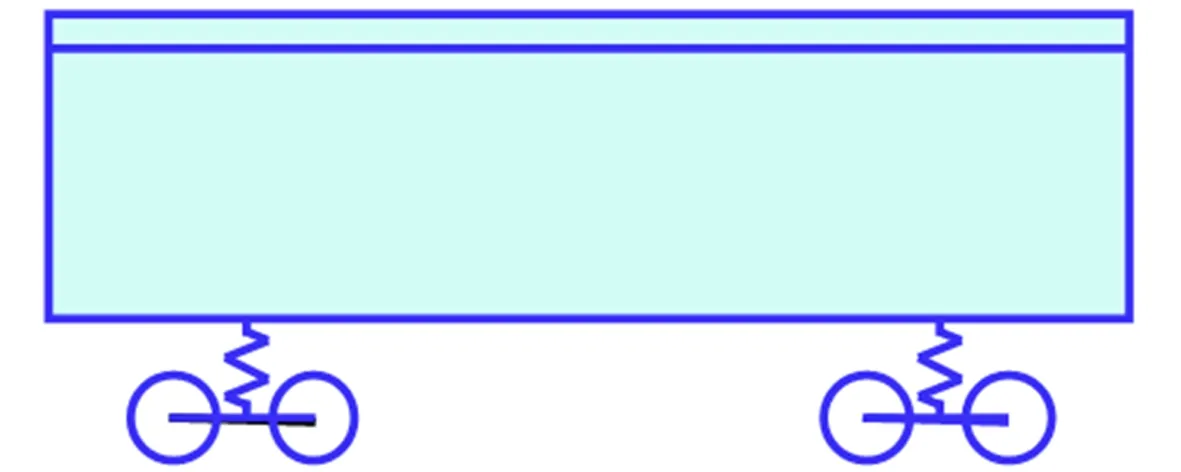
图1 车辆子系统多刚体动力学模型示意
其他计算条件:
①车辆采用中国标准动车组。
②验算速度至1.2倍设计速度,即100~480 km/h,每10 km/h一级。
③考虑梁端变形时用梁端过渡曲线模拟梁端区域轨道的变形曲线。
④考虑残余徐变变形影响时,假设每一跨均发生相同的梁体上拱,且上拱形状均为半正弦曲线。
⑤模型为5跨连续布置,支座为理想支座。
⑥考虑基础沉降时,按5跨梁中的第1~2梁之间、第3~4梁之间的基础沉降计算,每跨梁的工后基础不均匀沉降曲线仍按直线考虑,如图2所示。

图2 梁端线路处理方法示意
⑦不考虑轨道不平顺。

(1)
3 评判标准
采用的车桥动力响应指标:
①跨中动挠度应不大于设计活载挠度(含冲击系数),即列车通过时的跨中动挠度不应大于(跨度×挠跨比×设计活载动力系数)/2。
②跨中加速度不应大于5.0 m/s2。
③轮重减载率限值取0.25。参考日本在确定新干线桥梁刚度限值时,不考虑轨道不平顺情况下采用了反复出现的减载率不大于0.25[5]作为限值。
④不考虑轨道不平顺的影响,在车体加速度规范限值基础上考虑40%的安全余量,则车体加速度限值取0.6 m/s2(舒适度优秀)、0.78 m/s2(舒适度良好)、1.2 m/s2(舒适度及格)[6]。
4 理论分析
1)动挠度
不同桥梁刚度(以静活载挠度来表示,下同),无徐变无沉降情况下跨中动挠度与列车运营速度的关系见图3。可见,动挠度最大值发生在速度480 km/h左右,桥梁刚度越大,动挠度越小。最大动挠度3.43 mm,相当于单线设计活载动挠度的0.311倍,结构受力安全。
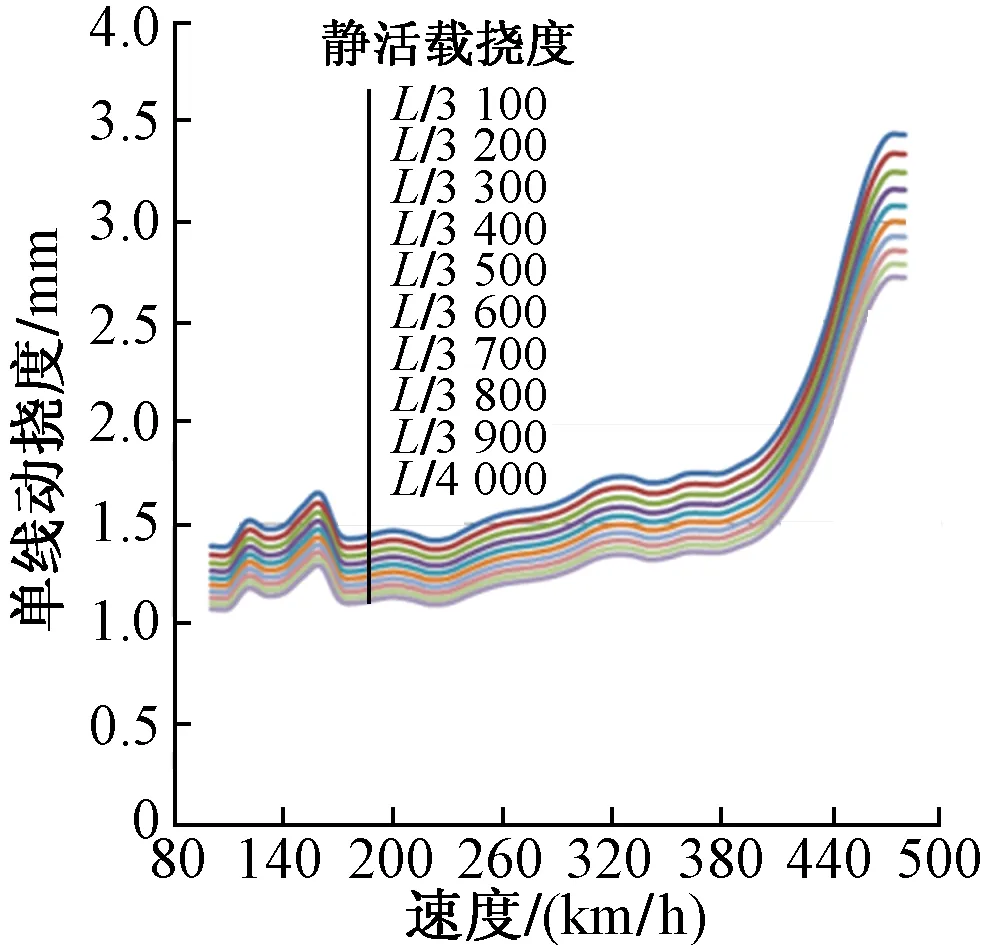
图3 无徐变无沉降情况下跨中动挠度与速度的关系
2)梁体跨中加速度
不同桥梁刚度、无徐变无沉降情况下梁体跨中加速度与列车运营速度的关系见图4。可见,梁体跨中加速最大值发生在速度480 km/h左右,桥梁刚度越大,梁体跨中加速度越小。最大跨中加速度为2.63 m/s2,满足限值要求。

图4 无徐变无沉降情况下梁体跨中加速度与速度的关系
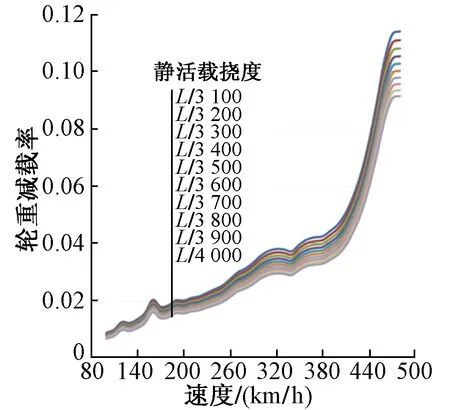
图5 无徐变无沉降情况下轮重减载率与速度的关系
3)轮重减载率
不同桥梁刚度、无徐变无沉降情况下轮重减载率与列车运营速度的关系见图5。可见,轮重减载率最大值发生在速度480 km/h左右,桥梁刚度越大,轮重减载率越小。最大轮重减载率为0.11,满足限值要求。
4)车体加速度
不同桥梁刚度的情况下,车体加速度与列车运营速度的关系见图6。可见,车体加速度最大值发生在速度480 km/h左右,桥梁刚度越大,车体加速度越小。最大车体加速度为0.30 m/s2,舒适度优秀。
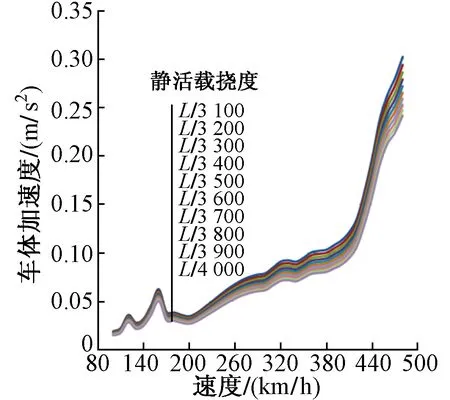
图6 车体加速度与列车运营速度的关系
5)徐变变形[7-8]、不均匀沉降的影响
通过分别设置徐变上拱5 mm、徐变上拱10 mm、沉降5 mm、沉降10 mm,计算车桥动力响应。计算结果见表1。可见:①徐变变形和不均匀沉降对动挠度影响较小;②徐变变形对梁体跨中加速度影响较大,徐变10 mm 时加速度超过限值;③徐变变形和不均匀沉降对轮重减载率影响均较大,徐变10 mm和沉降10 mm 时轮重减载率超限;④徐变变形和不均匀沉降对车体加速度影响均较大,徐变10 mm时舒适度不及格。
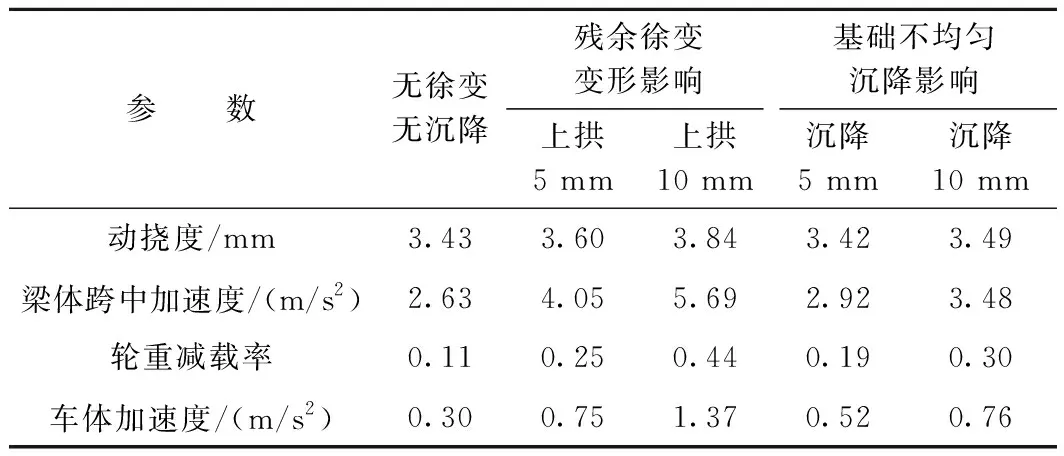
表1 徐变与沉降的影响计算结果
5 结论
1)速度在420 km/h以上时,车桥动力响应急剧增大,动力响应最大值均发生在最大计算速度(480 km/h)时。
2)桥梁刚度增加,车桥动力响应减小。
3)徐变变形和不均匀沉降对动挠度影响较小,对梁体加速度、轮重减载率、车体加速度影响较大。
4)新建设计时速400 km高速铁路32 m混凝土简支梁的设计标准建议值为:基频限值150/L;挠跨比L/1 600;梁端转角1.5‰rad(无砟);残余徐变上拱5 mm;工后基础不均匀沉降5 mm。其中挠跨比指标维持既有标准,是因为在满足基频的条件下混凝土简支梁均能满足规范限值。对于梁端转角的限值也维持既有标准,是因为其是轨道结构静态受力控制,并且在满足基频的条件下,混凝土简支梁均能满足规范限值。
5)对于时速400 km高速铁路,由于徐变影响较大,建议预应力混凝土简支梁进一步延后二期恒载上桥时间,降低残余徐变变形。
综上所述,对于32 m混凝土简支梁,新建时速400 km高速铁路设计参数基本与既有时速350 km高速铁路设计参数相当。
[1]国家铁路局.TB 10002—2017 铁路桥涵设计规范[S].北京:中国铁道出版社,2017.
[2]国家铁路局.TB 10621—2014 高速铁路设计规范[S].北京:中国铁道出版社,2015.
[3]夏禾,张楠.车辆与结构动力相互作用[M].北京:科学出版社,2005.
[4]刘晶波,杜修力.结构动力学[M].北京:机械工业出版社,2011.
[5]王天福.车辆动力学[M].北京:中国铁道出版社,1981.
[6]中华人民共和国铁道部.铁运[2012]83号 高速铁路无砟轨道线路维修规则(试行)[S].北京:中国铁道出版社,2012.
[7]王永宝,贾毅,廖平,等.混凝土收缩徐变预测模型对比分析[J].铁道建筑,2017,57(8):146-150.
[8]姜嫚.基于实测数据修正的徐变预测模型在铁路桥预拱度计算中的应用[J].铁道建筑,2014,54(5):5-8.
