混凝土弹性模量时变效应对刚构桥线形控制的影响
2018-06-28周小勇
孟 城,周小勇,陈 鹰,倪 林
(1.中国地质大学(武汉) 工程学院,湖北 武汉 430074;2.中铁十六局集团 第三工程有限公司,浙江 湖州 313000)
目前国内外公路及铁路桥梁广泛采用连续梁连续刚构组合体系桥。这类桥梁常采用悬臂施工法施工,施工过程中的线形控制主要都是通过设置预拱度来实现。预拱度可分为:为消除施工过程中各种荷载影响的施工预拱度;和为消除后期运营中的收缩徐变、预应力损失等影响的成桥预拱度[1]。
桥梁的施工控制通常采用建立有限元分析模型对桥梁的预拱度进行计算,综合考虑了材料力学指标、恒载、施工荷载、预应力等因素的影响,并根据现场实测数据结果调整桥梁分节段施工的立模标高值。其中材料力学指标包括混凝土重度、弹性模量、收缩徐变等。对于混凝土而言,随着时间的推移,水泥水化反应越来越完全,混凝土的抗压强度不断增大,弹性模量也随之不断增长。对于分节段悬臂施工的大跨径连续刚构桥,尤其是对线形要求更加严格的高速铁路桥梁,混凝土弹性模量的时变效应会对桥梁挠度产生很大的影响。桥梁线形是否平顺直接关系到成桥后高速铁路桥的安全。王长青[2]比较了不同的弹性模量取值引起的成桥挠度误差。刘俊等[3]研究了混凝土弹性模量对现浇梁段预拱度的影响。顾卫国[4]通过统计标准养护条件下的混凝土早期弹性模量和28 d弹性模量值,并通过3~90 d内同条件养护下弹性模量试验的验证,确定C55 混凝土弹性模量的时变规律。目前,国内规范没有对弹性模量的时变效应给出具体规定,在计算时常忽略弹性模量时变效应对挠度的影响。
本文以江西省吉安市泰和赣江特大高速铁路桥梁为工程背景,分析混凝土弹性模量时变效应对连续刚构桥线形的影响。
1 计算模型
1.1 工程概述
昌赣高速铁路泰和赣江特大桥跨径(48+80+160+80+48)m,全长417.5 m(含两侧两端至边支座中心各0.75 m)。主梁采用单箱单室箱形截面,箱梁梁高、底板厚度均按照二次抛物线变化,主梁上部对称。主梁采用C55混凝土,主墩采用C40混凝土。全桥有3个合龙段,包括1个中跨合龙段和2个边跨合龙段,主桥按照先中跨后边跨合龙的顺序施工,全桥布置见图1。
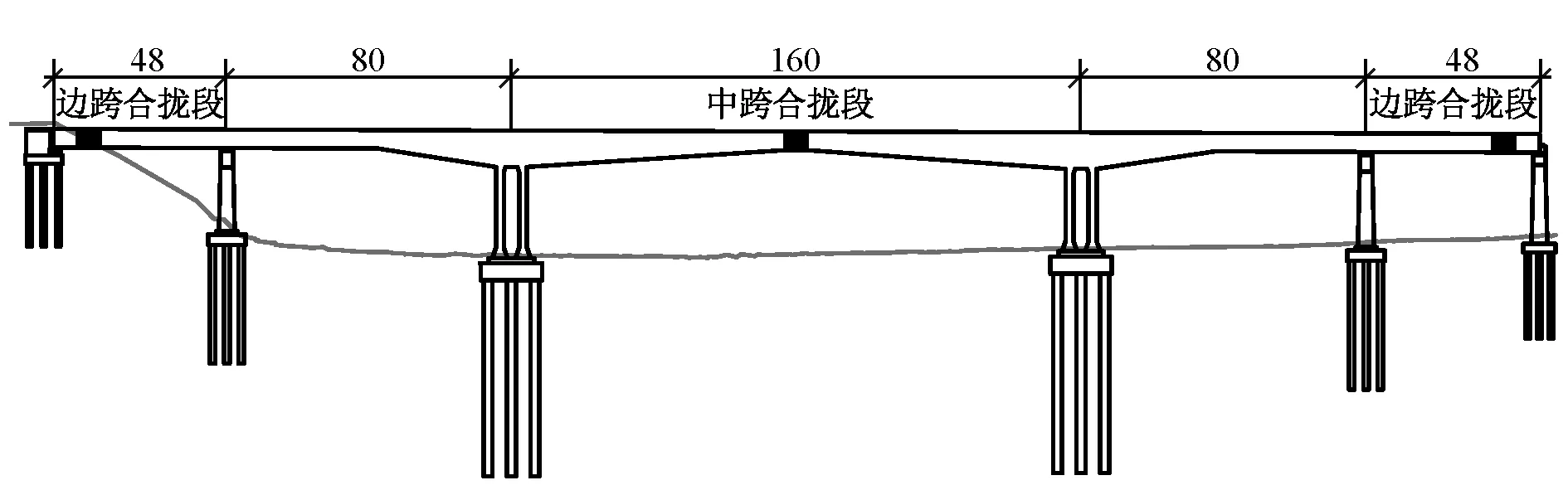
图1 桥型布置(单位:m)
1.2 桥梁有限元建模
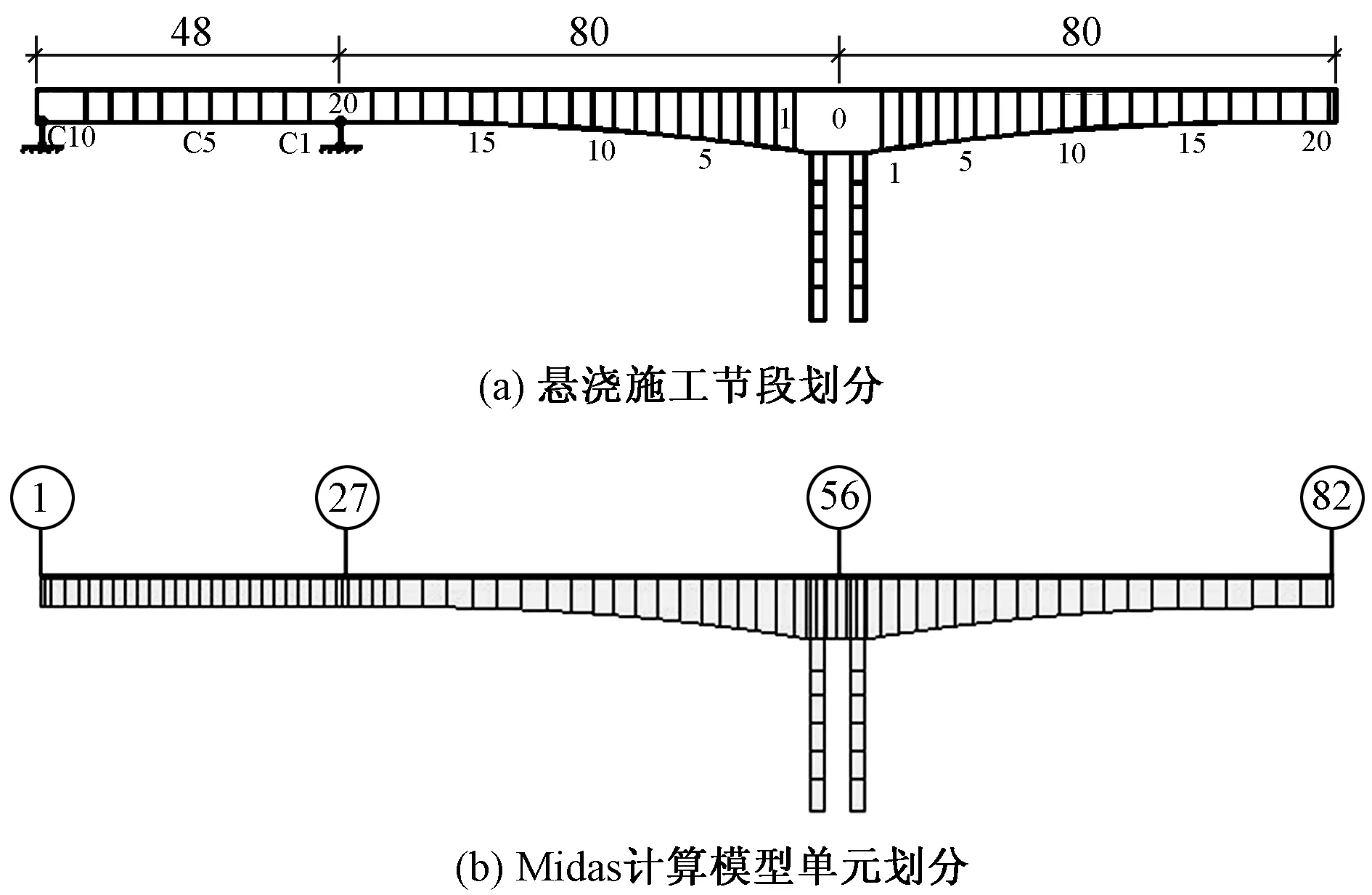
图2 主梁节段划分及模型(单位:m)
采用MIDAS/Civil软件建立桥梁有限元计算模型对施工阶段进行模型分析。全桥共划分193个节点,188个单元。其中164个单元为上部结构主梁单元,24个单元为桥墩墩身单元。主桥节段划分(取主桥一半)及有限元模型见图2。其中1号单元为主桥起始单元,27号单元为次边跨墩顶单元,56号单元为主墩墩顶单元,82号单元为中跨跨中合龙段单元。
2 弹性模量时变效应计算模型
2.1 国外规范弹性模量时变效应计算方法
2.1.1 ACI规范(美国)
ACI规定,混凝土强度等级采用圆柱体试件28 d抗压强度,并采用45%强度应力水平的割线模量作为混凝土的弹性模量[5]。其强度发展函数fck(t)如下
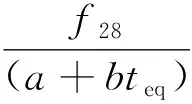
(1)
式中:f28为混凝土28 d抗压强度;a,b为混凝土抗压强度系数,一般取4.5,0.95;teq为龄期。
弹性模量计算函数Ec(t)如下
(2)
式中,wc为混凝土重度。
ACI规范将混凝土重度加入弹性模量的计算,更好地反应材料密度和骨料尺寸对弹性模量的影响。
2.1.2 CEB-FIP规范(欧洲)
CEB-FIP采用原点与0.4fck(其中fck为混凝土圆柱体抗压强度)连线的斜率作为混凝土的弹性模量。欧洲规范中同样采用了与中国规范相同的强度等级的概念。但对于同等强度等级混凝土,欧洲规范[6]中的抗压强度取值较大。其强度发展函数如下
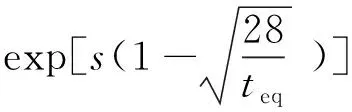
(3)
式中:s为水泥种类系数,取0.25。
弹性模量计算函数如下
(4)
2.1.3 日本规范
日本规范中强度发展函数如下
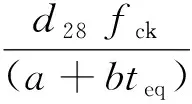
(5)
式中:d28为混凝土抗压强度系数,一般水泥取1.1。
弹性模量计算函数如下
(6)
2.1.4 韩国规范
韩国规范中混凝土抗压强度计算公式如下
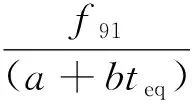
(7)
式中,f91为混凝土91 d抗压强度。
弹性模量计算函数如下
(8)
2.2 弹性模量现场实测数据
根据GB/T 50081—2002《普通混凝土力学性能试验方法标准》,在实际工程现场对施工所用C55混凝土进行弹性模量试验。混凝土弹性模量值在28 d龄期时趋于稳定,因此样品龄期选择3~10,12,14,16,18,20,24,28,32 d共计16组,每组6个试件,采用标准养护条件进行养护,各龄期所得弹性模量取试件测值的平均值,所得结果见表1。试验结果用于拟合出现场实测弹性模量值历时曲线。
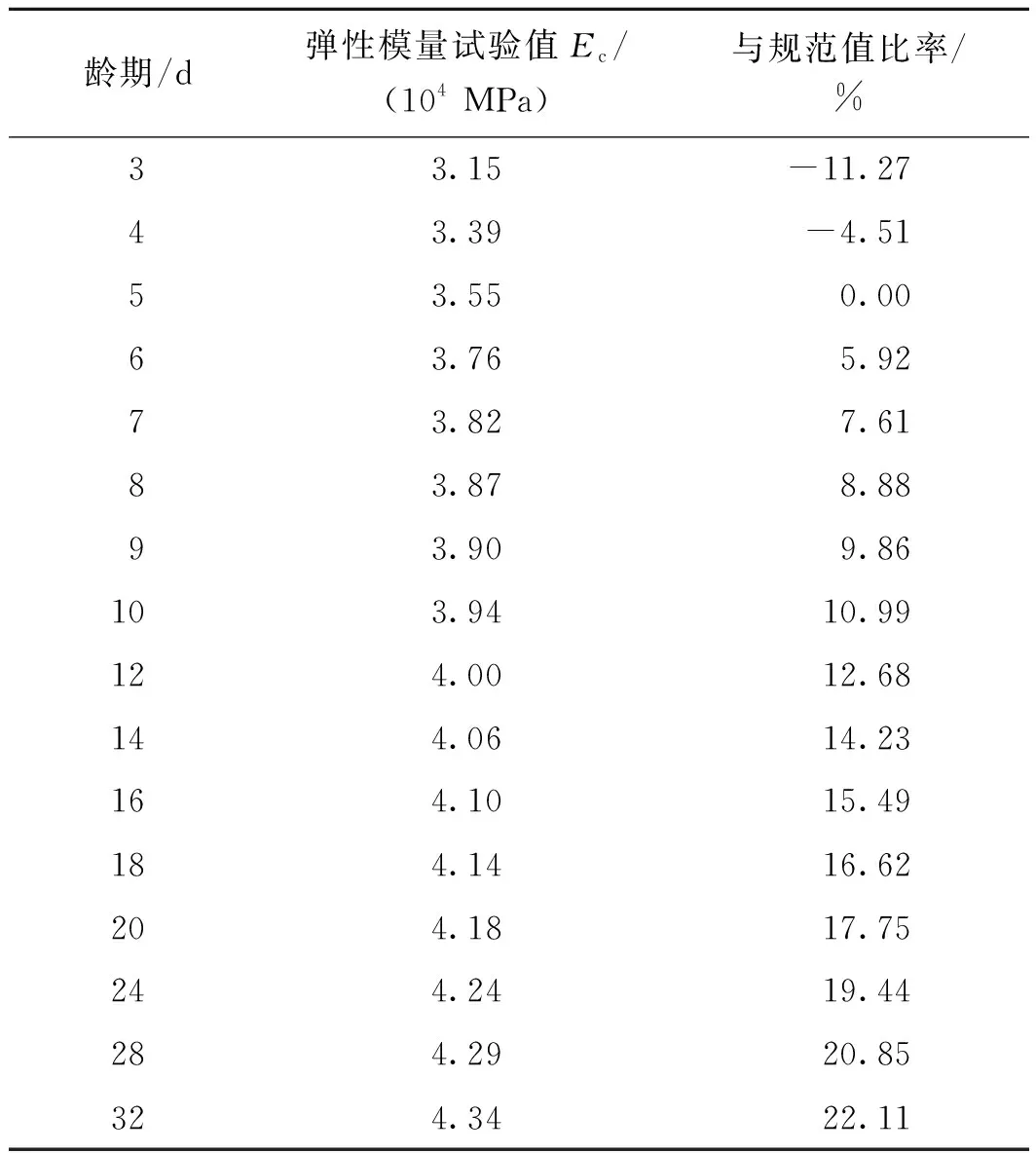
表1 现场C55混凝土弹性模量实测值
3 不同弹性模量时变模型的弹性模量和挠度
在有限元软件MIDAS/Civil中,可以通过设置各规范的强度发展函数来模拟混凝土弹性模量的时变效应,且可以自定义弹性模量时变效应函数。选取上文中的几种弹性模量时变模型,考虑仅在结构自重和收缩徐变的情况下,对全桥挠度进行计算。
3.1 弹性模量对比
通过定义终值使得在各规范计算公式下混凝土28 d龄期的弹性模量值近似于35.5 GPa,即C55混凝土弹性模量标准值。
将各规范、弹性模量标准值及现场测得数据等计算方法计算所得弹性模量加以对比,见图3。
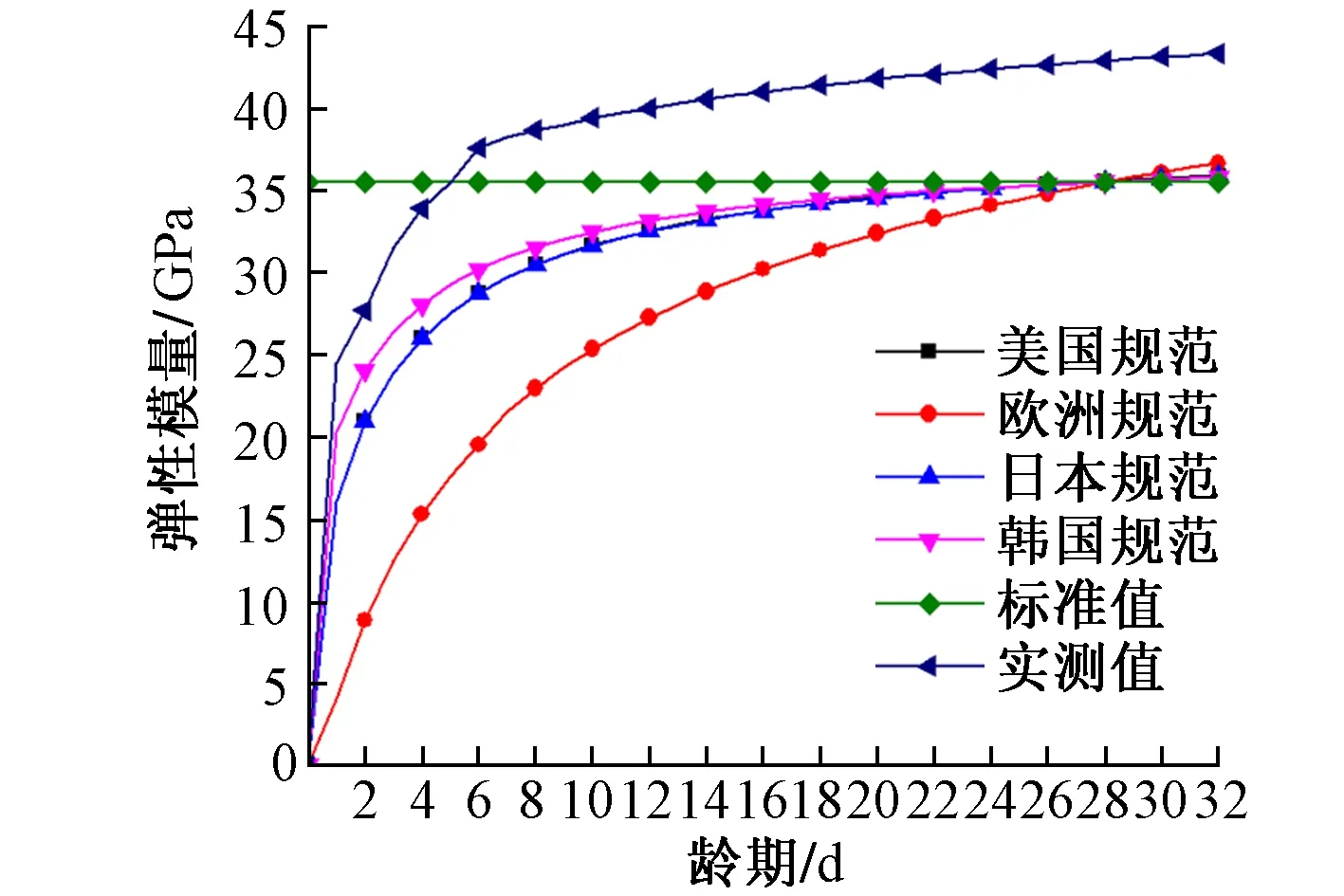
图3 C55混凝土弹性模量
由图3可知,不同弹性模量时变模型曲线存在以下特点:
1)根据美国、日本、韩国规范所得弹性模量时变效应曲线较为接近,在1~28 d龄期内存在较小差异;在28 d龄期后,该3种规范计算所得弹性模量曲线趋于一致。
中小型工业企业由于缺少人才和资金的支持,普遍存在研发能力较弱的情况,主要是企业家凭着一股韧劲带领科研队伍进行研发。然而新产品的研发需要投入大量的人力物力,经历无数次的失败和大额的资金损失,最终还不一定成功,新产品研发每前进一步都非常困难,新产品研发一旦失败,便会给企业带来巨大的资金压力和经营压力。
2)根据欧洲规范所得弹性模量时变效应曲线与其他曲线有较大差异,在1~28 d龄期内曲线数值小于其他计算结果;在28 d龄期后曲线仍然处于上升阶段。弹性模量的数值将随时间增长一直不断增大。
3)根据弹性模量实测结果可以发现,实际施工所用混凝土弹性模量发展与采用国外规范计算有较大区别。前28 d龄期中,现场测得混凝土弹性模量始终较大且发展较快,至28 d后趋于稳定。这是因为施工现场采用C55混凝土强度明显高于标准值,使得其弹性模量也高于标准值;由于实际施工的需要,施工单位要求龄期5 d时,现场使用混凝土弹性模量就需达到标准值。
3.2 主梁挠度对比
用不同弹性模量时变效应模型计算最大悬臂状态时泰和赣江特大桥主梁竖向挠度,结果见图4。
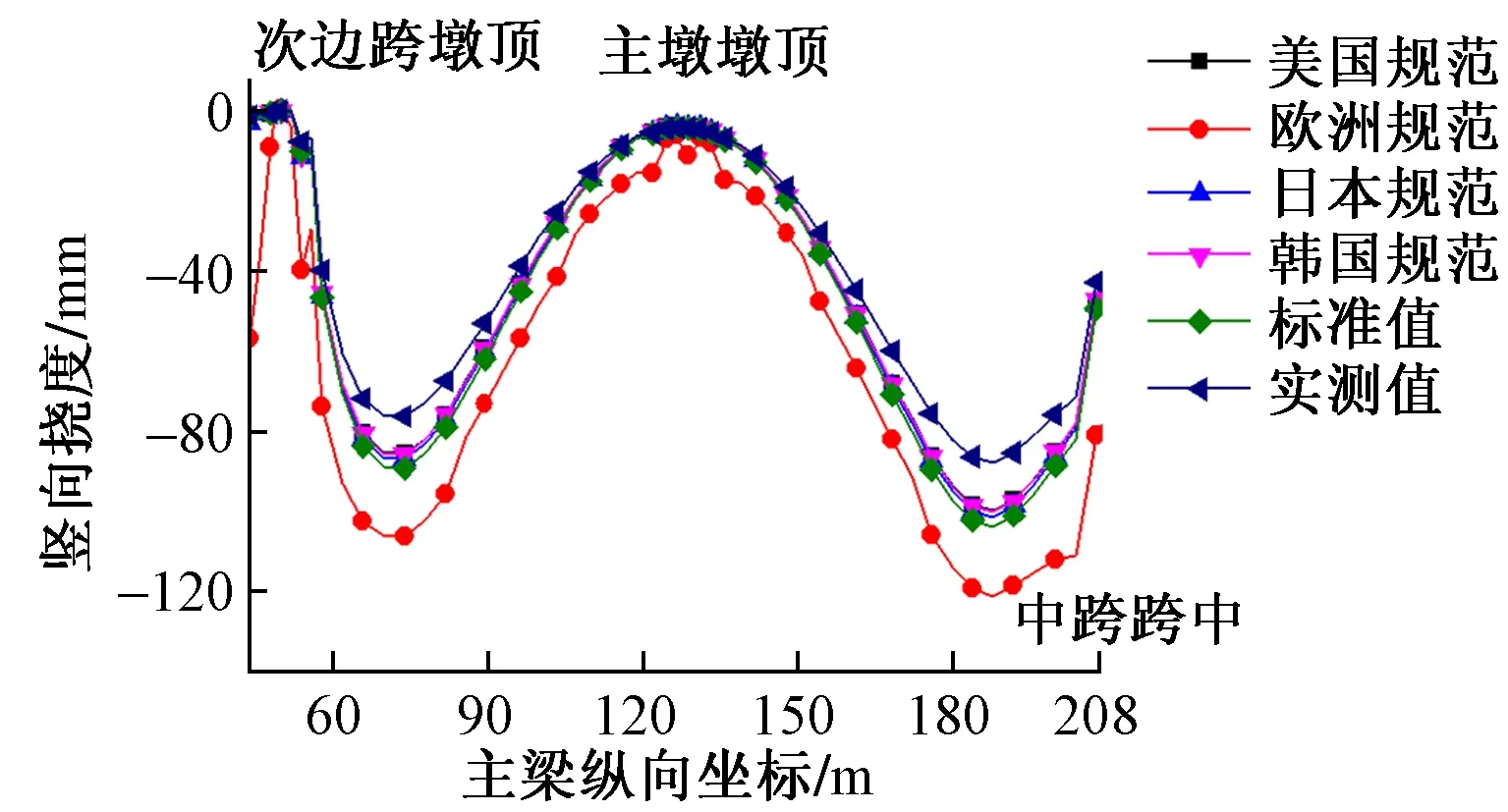
图4 最大悬臂状态主梁竖向挠度
由图4可知,最大悬臂状态下各模型计算结果差别主要存在于次边跨及中跨。美规、日规、韩规、固定值计算结果非常接近,欧洲规范计算结果中主梁产生的挠度最大,在中跨跨中处下挠值比其他模型大40 mm 左右,弹性模量实测计算结果的挠度最小,中跨跨中两侧挠度比其他模型小5~10 mm。
用不同弹性模量时变效应模型计算泰和赣江特大桥成桥后主梁竖向挠度,结果见图5。
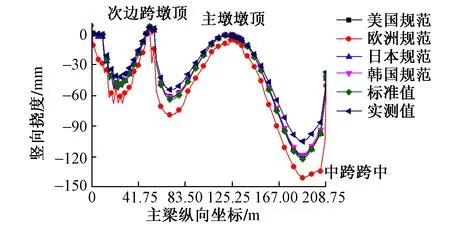
图5 成桥后主梁竖向挠度
由图5可知,在成桥后美国、日本、韩国规范计算的弹性模量与标准值依然较为接近。欧洲规范计算结果中,由于在1~28 d龄期内弹性模量远小于其他规范计算所得值,其成桥后挠度值最大,对中跨靠近跨中梁段的挠度影响最为明显,最大差值超过20 mm。弹性模量实测计算结果的挠度最小,中跨跨中两侧挠度比其他模型小5~10 mm。
结合以上计算结果可以得出以下结论:
1)弹性模量时变效应对桥梁成桥后挠度存在较大影响,尤其对各跨跨中梁段的影响较大,同时这也是施工控制的关键部位。28 d龄期前的弹性模量对成桥后桥梁挠度的影响最为明显;28 d龄期后弹性模量的时变效应对成桥后桥梁挠度的影响逐渐减小。
2)在施工监控中,由于我国没有相关规范规定弹性模量时变效应计算方法,通常不考虑弹性模量变化,利用MIDAS/Civil计算桥梁挠度所得的结果与采用美国、日本、韩国规范所得计算结果基本一致,而采用欧洲规范计算结果偏大。
3)现场实际与理论结果存在偏差。现场施工所用混凝土弹性模量及强度均大于标准值,因此施工监控常用计算方法所得预拱度一般大于采用现场测得数据计算所得值。理论与施工实际的偏差会影响到施工过程中立模标高的精确度,对于无砟轨道高速铁路桥,其成桥铺设轨道后竖向位移的控制值为20 mm[7-8],因此施工控制中应考虑弹性模量的时变效应。
4 考虑弹性模量时变效应的施工控制
为使桥梁成桥后实际标高与设计标高相吻合,实际施工过程中采用设置预拱度以控制桥梁线形。立模标高计算式为:立模标高=设计标高+预拱度+挂篮变形-顶板厚,其中挂篮变形在梁段施工前通过挂篮预压试验测得。为观测主梁变形,各节段在浇筑前设置标高观测点,每节段前端设置5个点,顶板布置3点,底板布置2点。
理论计算时混凝土弹性模量取值通常取标准值或采用国外规范中的时变模型计算值,因此预拱度的理论值与实际值存在差异。表2中对比了部分已浇筑梁段立模标高的理论值与实际值。
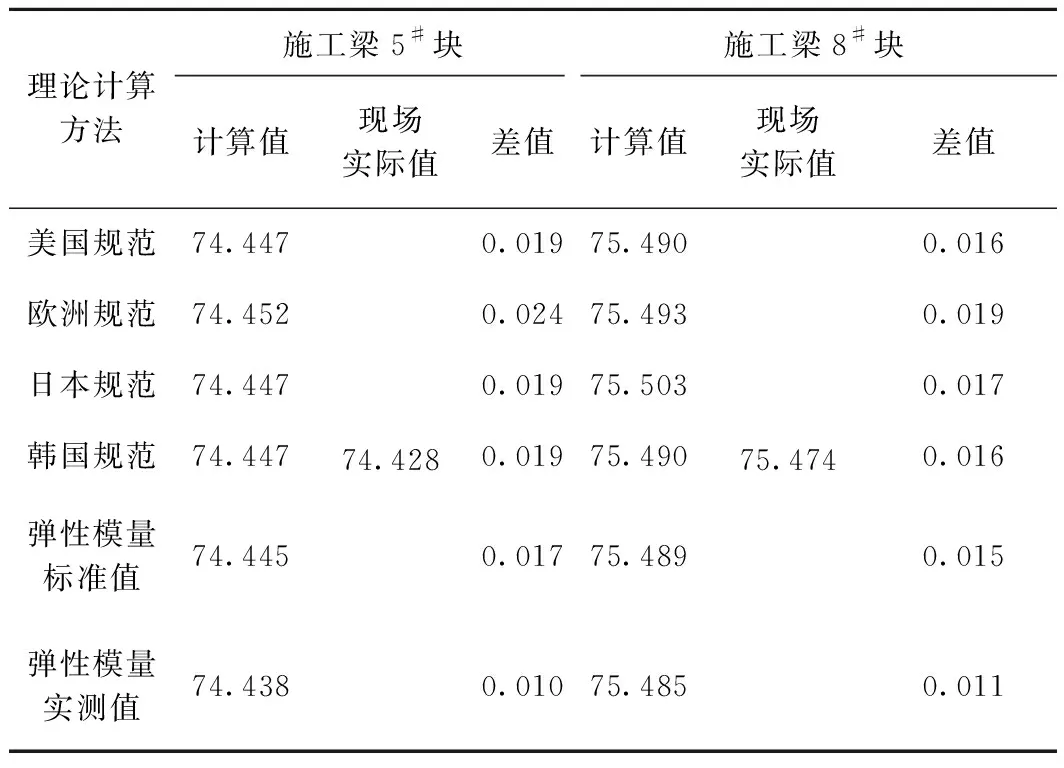
表2 2#墩靠跨中方向已浇筑段梁底标高比较 m
由表2可见,采用不同弹性模量时变模型计算所得立模标高均大于实际值。其中,现场实测拟合的时变模型计算结果与实际施工取值亦存在10~12 mm的差值;取定值或采用国外规范中的时变模型计算结果差值更大。此外,现场施工时标高监测往往不会明确预应力钢束张拉前后和挂篮前移引起的梁段变形,这使得现场实际值普遍较小。
在预应力钢束张拉、挂篮前移这2个施工阶段,悬臂梁段产生的变形同样会受弹性模量时变效应的影响,表3为各时变模型下部分梁段在不同施工阶段的竖向变形值。
由表3可见,弹性模量越小,张拉预应力钢束引起的梁段变形越大,且随着梁段的增加,张拉预应力引起的梁段变化值越来越大。挂篮前移后,不同梁段因挂篮下压引起的变形基本一致,受弹性模量时变效应影响较小。可见,混凝土弹性模量时变效应对梁段变形的影响应细化到各施工阶段进行分析。
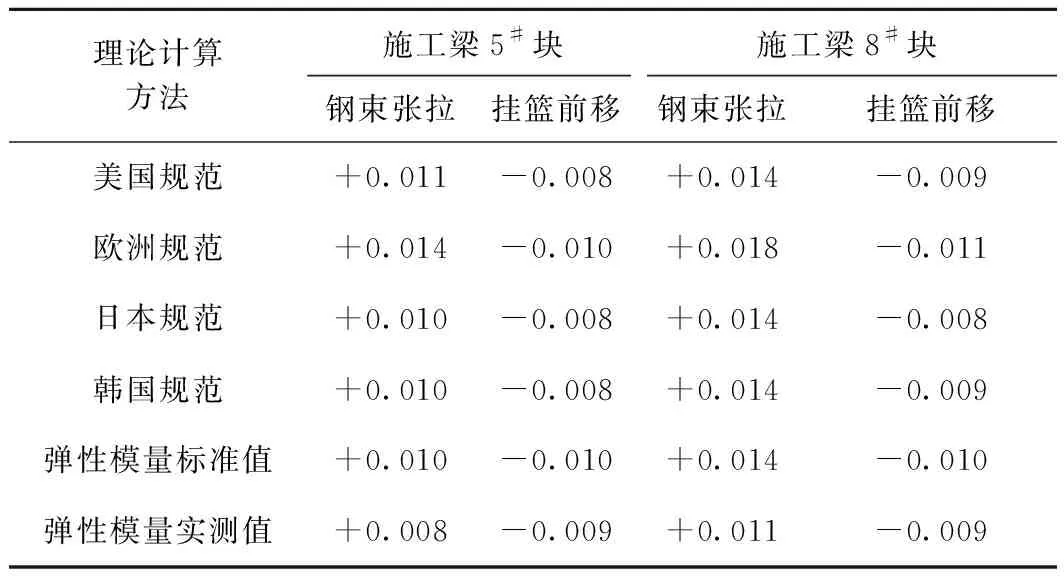
表3 部分梁段不同施工阶段变形值 m
注:“+”表示位移向上,“-”表示位移向下。
5 结论
1)预拱度的设置在大跨径连续刚构高速铁路桥桥梁施工控制中极为重要。常规的预拱度计算方法不够精细,没有考虑混凝土弹性模量的时变效应,计算所得的预拱度相对偏大,与实际差值将超过10 mm,难以满足高速铁路设计规范的要求。
2)在对桥梁结构进行预拱度计算时,应合理考虑实际施工现场中所用混凝土的力学性能指标。理论计算中弹性模量取值应尽量与现场试验结果相符。采用国外规范中的弹性模量时变模型时,应合理考虑弹性模量计算终值的选取,并通过现场试验对计算参数进行动态修正。
3)梁段标高测量应细化,标高测量应加入预应力钢束张拉前后和挂篮移动前后梁段标高的项目,将这两项引起的变形精细化分析控制,提高施工控制精度。
[1]向木生,张世飙,张开银,等.大跨度预应力混凝土桥梁施工控制技术[J].中国公路学报,2002,15(4):38-42.
[2]王长青.刚构连续梁桥施工控制中温度影响与设计参数调整的研究[D].武汉:武汉理工大学,2006.
[3]刘俊,陈铭.大跨径连续刚构桥施工控制研究[J].中外公路,2008,28(1):109-112.
[4]顾卫国.C55混凝土弹性模量时变效应对连续刚构桥的影响研究[J].工程建设与设计,2016(17):14-17.
[5]潘登,肖攀.中美规范混凝土材料强度值及弹性模量对比研究[J].建材与装饰,2014(18):23-24.
[6]夏进.中欧混凝土结构设计规范对比研究[D].武汉:武汉工程大学,2014.
[7]朱金涌.黄土高原地区高墩大跨T构桥线形监控研究[J].铁道建筑,2013,53(10):18-20.
[8]铁道第三勘察设计院集团有限公司.高速铁路设计规范[M].北京:中国铁道出版社,2014.
