一个经典概率问题的深度解析

马 冉 弭光伟 谢 玮

(河南理工大学数学与信息科学学院，河南，焦作454003）

1.问题重现

在概率统计中有这样一个概率问题：从1至9这九个数字中，有放回地取三个数字，每次任取一个，求所取的三个数字之积能被10整除的概率。

这是一道不起眼的概率题，由于一个不经意间的质疑，使它成为困扰学习者的难题。此问题是经典问题，也是一个易错的问题，本文就这一问题进行了深度挖掘和分析，给出了三种正确解法，分析了三种常见的错误解法。在尝试解决这个问题的过程中，我们找到了不同的解决方案。这能使学习者深受启发，受益良多，能更深刻地理解概率论中的基本定义和定理，并熟练解决此类古典概型问题。

2.问题求解

2.1 运用古典概型求解

运用古典概型求解，其重点也是难点就是如何把事件的所有可能情况都找出来，无错误不重复。对于此问题，通过分析可知要想被10整除，取出的三个数中至少有一个5和一个偶数。因此有三种情况：第一种，两个5，一个偶数；第二种，一个5，两个偶数；第三种，一个5，偶数和奇数各一个。下面进行详细分析。

（1）两个5，一个偶数。有以下情况：前两个数选 5： 5,5,2；5,5,4；5,5,6；5,5,8；首尾选 5：5,2,5；5,4,5；5,6,5；5,8,5；

后两个数选 5： 2,5,5；4,5,5；6,5,5；8,5,5；

（2）一个5，两个偶数。又可细分为两种情况：

①两个偶数相同：5,2,2；5,4,4；5,6,6；5,8,8。由于5的位置也可以在另外两个位置，所以此种情况共有 4×3＝12种情况。

② 两 个 偶 数 不 相 同 ：5,2,4；5,2,6；5,2,8；5,4,6；5,4,8；5,6,8。由于三个数均不同，所以三个数可以任意排列，有=6×6=36种情况。

综①和②，共有 12＋36＝48种情况。

③一个5，偶数和奇数各一个。

首先，确定 5和一个偶数（如 2）：5,2,1；5,2,3；5,2,7；5,2,9。 由于偶数有 4 个（2,4,6,8)可供选择且三个数各不相同，所以这三个数可以任意排列，故有 4×4×=4×4×6=96 种情况。综上三种情况，共有 12＋48＋96＝156 种情况。若设事件 “A=所取的三个数字之积能被10整除”，则有。

故所取的三个数字之积能被10整除的概率为 0．214。

2.2 运用条件概率中的全概率公式求解

记事件“A”为“所取的三个数字之积能被10整除”,事件“B”为“所取三个数中含有 5”。 则事件“”为 所取三个数不能被10整除，“”为所取三个数不包含5。则由全概率公式可知：

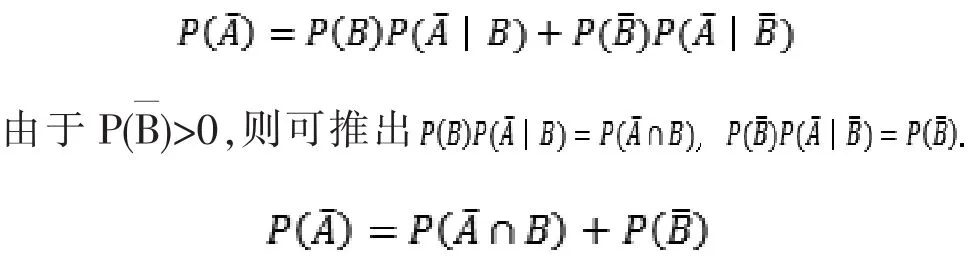
则事件“∩B”为“取到 5但不能被 10整除”，即“全奇数且有 5”，则有

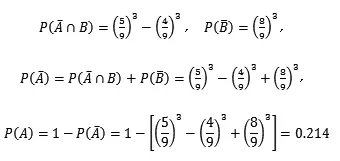
该方法主要用条件概率的全概率公式来求解。用事件取的三个数能不能取到5来进行分割，事件“”所取的三个数不能被10整除既包括所取三个数不包含5又包括所取三个数包含5这两种对立的情形，用全概率公式来进行求解。

2.3 运用事件的独立性求解

记事件 “A”为 “所取三个数能被十整除”，“A1”为“所取三个数中含有 5”，“A2”为所取三个数中含有偶数，则 A＝A1A2，所以

考虑到三次取数相互独立，。所以

该方法主要运用了事件的独立性，因为有放回的取三个数，所以第一次、第二次和第三次取数相互独立互不影响.

3.常见错误分析

错误一：

记事件“A”为“所取的三个数字之积能被10整除”，有

故所取的三个数字之积能被10整除的概率为 0．049。

分析：把问题想得过于简单，漏掉了一些情况，只列出了 2.1中正确解法中（1）的 4种情况，（2）①中的 4 种情况、（2）②中的 12 种情况，（3）的16种情况。也就是说这种做法只想到了（1）中三种位置的一种，漏掉了8种情况；（2）②中把5的位置固定了，漏掉了8种情况；（2）②同样把5的位置固定了，漏掉了 24种情况；（3）中把先确定的5和一个偶数位置固定，漏掉了80种情况。

还有一种类似的错误，如下：

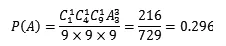
这种做法在上面做法的基础上想到了排顺序，但是直接全排就把一些情况又重复了一遍，即把有两个5和有两个偶数的情况多算了一遍，也就是说把（1）和（2）算了两遍，共重复了 12＋48＝60种情况。错误二：

记事件“A”为“所取的三个数字之积能被10整除”，可分为三种情况：

（1）两个 5，一个偶数：

（2）一个 5，两个偶数:

（3）一个5，偶数和奇数各一个：

共有12+48+48=108种情况。则有

分析：（1）和（2）两种情况是对的，而（3）中 C2表示在三个位置中选两个位置（不考虑排序）

3放一个奇数和一个偶数，显然不考虑排序是错误的，因为有奇数和偶数不可能相同，故应为

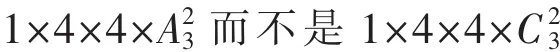
而（1）和（2）按照这种做法就是正确的，因为两个5和两个偶数的情况只需选位置即可。

总结：以上错误提醒我们在用古典概型的方法求解时要把问题想全面，做到不少不重复，容不得丝毫错误。

错误三：

错误重现：记事件“A”为“所取三个数能被10整除”， “A1”为“所取三个数中至少含有一个 5”，“A2”为“所取三个数中至少含有一个偶数”，则有

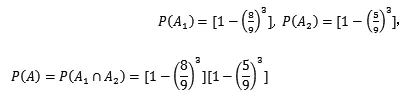
分析：该方法主要错误在于错误的认为 p(A1∩A2)=P(A1)P(A2)，而 A1，A2并不互相独立，所以 P(A1∩A2)≠P(A1)P(A2)。

[1]茆诗松，程依明，濮晓龙.概率论与数理统计[M].北京：高等教育出版社，2011:2.

[2]左振钊,张艳红.利用概率的古典定义求概率常见错误解法分析[J].河北北方学院学报(自然科学版),2006，22（4）：4-6.

[3]马冉，姬玉荣，郑玉歌.对概率论中有关问题的探索与推广[J].河南理工大学学报（自然科学版），2009，28（4）:543-546.

[4]马冉，任俊峰.生活中的概率课堂[J]．数理化学习，2010(1)：77-78.

[5]马冉，姬玉荣.数学建模思想在概率统计教学中的融入[J]．数学学习与研究，2010(1):1.