Thermodynamic properties of San Carlos olivine at high temperature and high pressure

Chang Su•Yonggang Liu•Wei Song•Dawei Fan•Zhigang Wang•Hongfeng Tang

1 Introduction

To get a better understanding of the composition and dynamics of the mantle,it is important to determine the thermodynamic properties as a function of the depth of the common minerals in the Earth’s interior(Akaogi et al.2007;Chen et al.1996;Li et al.2017).Thermodynamic parameters such as heat capacity and thermal expansion of mantle minerals are related to both geodynamics and mineral physics,and their values at high pressure are major factors that controlling the Earth’s internal evolution(Yoneda et al.2009).

Thermal expansion of mantle minerals largely depends on temperature and pressure,which can be deduced from experimental measurements on volume(Anderson 1967).Additionally,heat capacity at ambient pressure can be obtained using calorimetric experiments(Ashida et al.1987;Barin et al.1973;Watanabe 1982)or theoretical calculations(Akaogi et al.1984;Jacobs et al.2017;Price et al.1987).By using transient hot-wire method,the specific heat can be directly measured,but only in a lowpressure range(Andersson and Ross 1994;Nesbitt et al.2017).Osako et al.(2004)presented a new method to obtain the high pressure heat capacity in terms of simultaneous thermal conductivity and thermal diffusivity measurement(Osako et al.2004).Heat capacity of the solids is considered to be virtually independent of pressure(Navrotsky 1995),and its pressure derivation is sometimes ignored.However,considering its importance in calorimetric study,it is still worth determining the heat capacity for common mantle minerals at high pressure and its pressure dependence.

Davis and Gordon introduced a numerical procedure which can be used to derive the equation of state(EoS)(Davis and Gordon 1967).This equation set is based on a series of classical thermodynamic relationships,allowing accurate determination of the volume of a liquid as a function of pressure and temperature from experimental adiabatic sound velocity.This method has been applied on other melts or solutions(Ayrinhac et al.2015;Chorazewski et al.2013;de Koker 2012;Su et al.2017),thus proving its reliability.The accurate results show that this method is independent of any knowledge about compression in solid phases,and the sound velocity as a function of density follows a scaling law valid across the entire metallic state regime.But as far as we know,this numerical procedure is rarely used in single cell or polycrystalline minerals.

In order to test the feasibility of this method on minerals,we chose San Carlos olivine as our research material.San Carlos olivine is the ultramafic inclusion that is located in San Carlos,Arizona with a Mg:Fe ratio of 9:1[(Mg0.9-Fe0.1)2SiO4](Frey and Prinz 1978),which is the approximate composition of the peridotites in the mantle(Kojitani et al.2016).Olivine is a major component of the upper mantle(Liu et al.2005),and the determination of its thermodynamic properties is one of the most important themes in mineral science(Jianping et al.1995).The phase transition of olivine into its high pressure polymorph wadsleyite at～ 13–14 GPa is considered to be the most likely cause of the discontinuity at 410 km depth,from which the temperature of the 410 km discontinuity can be deduced from the thermodynamic changes.Because of this,numerous amount of studies have been carried out that provide the elastic properties of San Carlos olivine in a wide pressure and temperature range(Abramson et al.1997;Darling et al.2004;Isaak 1992;Liu et al.2005;Mao et al.2015;Zhang and Bass 2016).

In this study,using our original research and data from previous studies,we report the molar volume,thermal expansion,adiabatic bulk modulus and shear modulus of San Carlos olivine at high temperature and high pressure extracted with the numerical calculation.Then,we compare our findings with previous scholarship.Specifically,we present the thermal expansion and heat capacity of San Carlos olivine to 14 GPa and provide an equation that relates to both temperature and pressure.Finally,using the thermal expansion and heat capacity data of San Carlos olivine,we propose the temperature gradient of the upper mantle.

2 Calculation procedure

2.1 Thermodynamic calculation

We used data provided in Davis and Gordon(1967)to determine the calculation procedure and obtain the EoS of San Carlos olivine and its thermodynamic parameters as a function of temperature and pressure.This method uses classical thermodynamic relations to extract the density variation as a function of pressure and temperature from the adiabatic sound velocities.The fundamental equations are described below.

First,the thermal expansion(α)is defined as:

Then,according to the definition of heat capacity(CP),its variation with pressure can be evaluated as Eq.(2),which is based on the Maxwell relation:

Furthermore,the partial differential equation about the density at high pressure can be derived from the relationship between the isothermal and adiabatic bulk modulus:

where v stands for the sound velocity,and in the past only P-wave velocity was used in the previous works on liquids(Ayrinhac et al.2014,2015;Su et al.2017).To test whether this method could be applied to solids or not,we made a change on Eq.(3)to use the bulk velocity(vB)instead:

To start the calculation, first we calculated ρ as a function of temperature at zero pressure ρ( P0，T)and α at ambient pressure with Eq.(1).It is also necessary to determine the values of the heat capacity with increasing temperature CP(P0，T)in order to derive the approximate ρ at an arbitrary reference pressure using Eq.(2).The resulting ρ is used to update the value of αPand CPat the same pressure with Eqs.(1)and(2).Iteration of this loop leads to converged values of ρ,αPand CPat high pressure conditions.Furthermore,with the deduced results,the adiabatic bulk modulus(KS)and shear modulus(G)can also be obtained:

2.2 Thermodynamic data

2.2.1 Sound velocity at high temperature and high pressure

The sound velocities of San Carlos olivine have been investigated using different experimental methods(Abramson et al.1997;Darling et al.2004;Isaak 1992;Liu et al.2005;Mao et al.2015;Zhang and Bass 2016).Isaak first reported the high temperature elastic moduli for Febearing olivine,which provided various parameters as a function of temperature at ambient pressure(Isaak 1992).Then Abramson et al.(1997)measured the sound velocities up to 17 GPa at room temperature in a diamond anvil cell,and the results were consistent with those given by Darling et al.,which were obtained with a Kawaii type multi-anvil apparatus(Darling et al.2004).The highest temperature and pressure range data available to date was determined by Zhang and Bass,who used the Brillouin spectroscopy with CO2laser-heating and calculated the sound velocities of San Carlos olivine to 16.5 GPa at room temperature and 12.8 GPa at 1300 K(Zhang and Bass 2016).

Though this research provides useful data on the elastic properties of the olivine in a wide range of P–T conditions,what is needed is more detailed sound velocity data on a smaller interval of temperature and pressure.The data published by Liu et al.(2005)and Mao et al.(2015)provide sound velocities at both high temperature and high pressure conditions.With a DIA type large volume apparatus,Liu et al.(2005)measured the P-wave and S-wave sound velocities of the polycrystalline San Carlos olivine to 8 GPa and 1073 K,while Mao et al.(2015)analyzed natural single crystals using the high P–T Brillouin measurements,which provided a smaller difference between the experimental data and the isothermal fitting results.Therefore,in this paper,we used Mao’s sound velocities of San Carlos olivine.

Using thevpandvsdata from Isaak(1992),we determinedvpandvsto analyze the high P–T data to ambient pressure,thus permitting us to obtain the P–T–v relationship as Eq.(7),whose form is based on the work by Ayrinhac et al.(2015):

The fitting coefficients are shown in Table 1,with a reduced χ2as 2.35 forvpand 3.85 forvs,respectively.

2.2.2 Density at ambient pressure

The densities of San Carlos olivine at room temperature and ambient pressure are given as 3353 kg m-3in Isaak(1992),which were measured using the Archimedes immersion technique.Then Abramson et al.(1997)reported the density as 3355 kg m-3using the buoyancy method,and this resultisclose to the value of 3360 kg m-3based on the lattice constants.Zha et al.(1998)measured the density with X-ray diffraction and found a value of 3343 kg m-3,which is in agreement with the latest data 3341 kg m-3using the same method(Zhang and Bass 2016).For the α,here we chose α =3.304 ×10-5+0.742×10-8T-0.538T-2K-1by Fei(1995)based on the experimental data of Suzuki(1975).Therefore,a reliable extrapolation of ρ to high temperature can be constrained by previous studies:

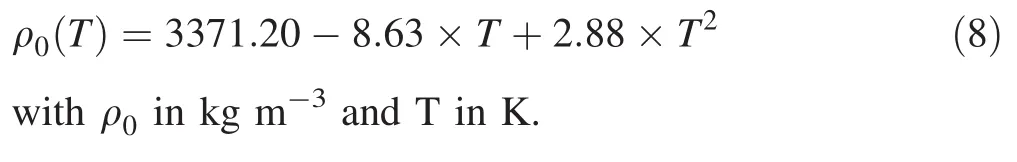
2.2.3 Heat capacity at ambient pressure

The heat capacity of San Carlos olivine at ambient pressure was also provided by Isaak(1992),which was determined from the end-member heat capacity data from Barin et al.(1973).Richet presented a way to obtain the heat capacity of the silicate glass with increasing temperature(Richet 1987),and he found that the value depended on the composition of the silicate glass.In Richet’s(1987) fitting equation,the temperature limit was lower than 800 K.In our calculation,we determined the values of heat capacity to be greater than 800 K,so in this work,we used Isaak’s ambient pressure heat capacity data.Berman and Brown gave a revised formula that represented and extrapolated the heat capacity with increasing temperature(1985),which was based on the lattice vibration theory,hence the fitting equation is:

withCPin J kg-1K-1and T in K.

With the data listed above,we derived the density,thermal expansion,heat capacity,adiabatic bulk modulus and shear modulus of San Carlos olivine under different temperature and pressure conditions.

3 Results and discussion

3.1 EoS and elastic properties comparisons

For the EoS of San Carlos olivine,the room temperature volume was measured using impulsively stimulated laser scattering to 17 GPa by Abramson et al.(1997)and later,using Brillouin spectroscopy to～30 GPa by Zha et al.(1998).The high temperature volume data was determined to 1073 K and 8 GPa using in situ synchrotron X-ray diffraction measurements(Liu and Li 2006).Figure 1 illustrates the molar volume of San Carlos olivine with increasing temperature and pressure,as well as the former results as comparisons.

Table 1 aijcoefficients for Eq.(7)with v in m s-1,T in K and P in GPa

From Fig.1,we can see that the calculated results generally agree with the previous experimental data(Abramson et al.1997;Liu and Li 2006;Zha et al.1998).At room temperature,our results show a similar trend with Abramson’s results,with a difference of～ 0.4%.The largest separation between our result and the other two works is 0.3%at 2.8 GPa.At high temperatures,our theoretical data is consistent with the experimental data,with a reduced χ2=7.63.As we mentioned above,the ambient pressure density data we used were obtained from theoretical calculations,so its difference from the experimental data was predicted to be large.However,with the increasing pressure,we can see that the separations became smaller,especially over～4 GPa.Hence,though different measurements would likely give data with different uncertainties,because of the self-consistency of the thermodynamic parameters,the calculated results could be fixed when using this theoretical method,which would finally provide reliable results.

Fig.1 Molar volume of San Carlos olivine as a function of pressure at different temperatures[curves:theoretical results from this work;solid circles:experimental results from Liu et al.(2005);insert:room temperature data with previous work]

The other quantities derived from our calculation are adiabatic bulk modulus and shear modulus.Based on Hashin–Shtrikman bounds,the aggregate KSand G of San Carlos olivine have been determined to 3 GPa(Webb 1989),17 GPa(Abramson et al.1997)and 32.5 GPa(Zha et al.1998)at room temperature using various techniques.For high temperature data,Liu et al.(2005)provide the values not only of KS0,G0and their pressure derivation,but also their temperature derivation to 8 GPa and 1073 K(Liu et al.2005).Mao et al.(2015),whose sound velocities we utilized in our calculation,calculated the elastic moduli of San Carlos olivine to～18 GPa and 900 K.With the density data of San Carlos olivine as a function of both temperature and pressure,the values of KSand G can be obtained with Eqs.(5)-(6),thus our calculated results are shown in Fig.2 along with the previous works.

Figure 2a,b illustrate the KSand G with increasing pressure at room temperature and high temperature,respectively.Generally,for KS,its values follow a nearly linear increase with pressure under same temperature,whereas G exhibits a downward trend towards higher pressure.In Fig.2a,our results agree with the former ones and are close to Mao’s results,which gives a largest separation as 0.4%at～14 GPa for both KSand G.This likely occurs due to our use of Mao’s sound velocity data during our calculation.For KS,all of the works consistently agree with each other except for Liu et al.(2005)’s data,whose slope is steeper than the others.For G,the separations get larger above～5 GPa,and our slope gets smoother comparing to the others.In Fig.2b,the differences seem to be quite large from different methods,especially under～6 GPa,butthen the consistency between our results and Mao et al.’s(2015)results improves with increasing pressure.

Fig.2 Comparison of adiabatic bulk modulus and shear modulus.a Room temperature condition.b High temperature condition.Blue:500 K;red:750 K;green:900 K; filled areas:Liu et al.(2005);dash lines:Mao et al.(2015);solid lines:this work

3.2 Thermal expansion and heat capacity at high temperature and high pressure

For the thermodynamic parameters deduced from Eqs.(1)–(4),here we present the thermal expansion and heat capacity of San Carlos olivine under different temperatures with increasing pressure in Figs.3 and 4,respectively.

The thermal expansions of minerals at high pressure are usually related to their volumes by the Anderson-Grüneisen parameter(δT),which describes the degree of decrease in α by compression(Anderson 1966).The expression is:

where α0is the thermal expansion at ambient pressure andV0,VPare volumes at ambient pressure and high pressure,respectively.In this work,the value of δTis calculated as 7.15±0.6,which is similar as forsterite(7.2±0.3,Katsura et al.,2010).Furthermore,the product of thermal expansion and isothermal bulk modulus(αKT),which can be considered volume-independent within the investigated pressure and temperature range,is 4.02±0.35×10-3,and this result is close to the value given by Liu and Li(4.08±0.10×10-3,2006).

Fig.3 Thermal expansion of San Carlos olivine as a function of pressure at different temperatures

Fig.4 Heat capacity of San Carlos olivine as a function of pressure at different temperatures

Most of the data about the heat capacity of olivine or other minerals are obtained at ambient pressure using calorimeters(Akaogi et al.2007;Robie et al.1982;Watanabe 1982),and the sources at high pressure are still rare.Though the heat capacities have been measured in the piston cylinder(Andersson and Ross 1994;Hashimoto et al.2006),the pressure range was limited to 2 GPa.Actually,the experimental method to measure the heat capacity directly continues to be a problem because of the difficulty of obtaining calorimetric measurements in high temperature and high pressure(Yoneda et al.2009).In mineralogy,heat capacity is usually related to thermal conductivity(λ)and thermal diffusivity(κ),hence in 2004,a method to obtain the heat capacity was developed by Osako et al.(2004),which simultaneously measured λ and κ at high temperature and high pressure,thus permitting for the heat capacity to be calculated.Osako et al.(2004)measured the λ and κ of San Carlos olivine,which provided the pressure derivation of its heat capacity(dC/dP)and the values of the CP/dP changed for different crystal axis.Also,the value of dCP/dP deduced from the ambient pressure data was also presented(Suzuki 1975;Watanabe 1982).

In Fig.5,we illustrate the heat capacities with increasing pressure at room temperature,which are calculated using Eq.(12)and the values from Watanabe(1982)and Osako et al.(2004).At ambient pressure,ourCP|P=0is 814 J kg-1K-1,which is close to the values from Watanabe’s result.Also in combining data of Watanabe(1982)and Suzuki(1975),in Fig.5,we can see that the variations among the slopes from different axis are large,except for the[1 0 0]one,whose slope is-1.5,thus making it quite similar to Watanabe’s(1982)results.Meanwhile,our result is consistent with that of Watanabe,and the slope is dCP/dP=3.67×10-2P-1.43,where P is in GPa.Since the error of the heat capacities from Osako et al.(2004)is 6%,our results still coincide with theirs(Osako et al.2004,Watanabe,1982).

Fig.5 Heat capacity vs pressure at room temperature with previous work

3.3 Temperature gradient to 410 km

One of the most important applications of thermal expansion and heat capacity at high pressure is used to estimate the temperature gradient in the Earth’s interior.Since conductive and radiative heat transfer can be ignored because of the small thermal conductivity of mantle minerals,the temperature gradient is considered to be nearly adiabatic.Therefore,the adiabatic temperature gradient can be expressed as:

where z is the depth,g is the gravitational acceleration(Katsura et al.2010).

To calculate the temperature gradient in the upper mantle,we extrapolate the thermal expansion and heat capacity to the pressure and temperature range at the 410 km discontinuity in the mantle.Considering the temperature range in this study,it should be an adequate approximation to treat thermal expansion as linear in temperature at ambient pressure(Katsura et al.2010).For heat capacity,its variation with increasing temperature at ambient pressure can be fitted using the model from Berman and Brown(1985).As seen in Figs.3 and 4,both thermal expansion and heat capacity at high pressure can clearly be presented by a polynomial fitting equation,thus with the data derived from Eqs.(1)–(4),the thermal expansion and heat capacity of San Carlos olivine as a function of both temperature and pressure can be expressed as Eqs.(12)and(13).

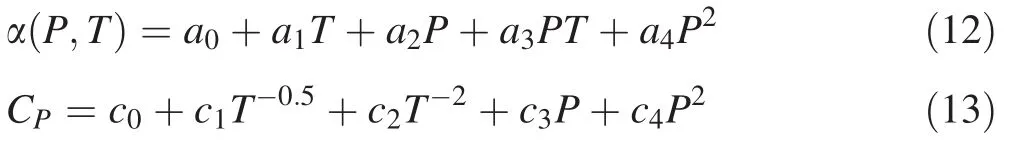
The fitting coefficients for Eqs.(12)and(13)are listed in Tables 2 and 3,respectively.The misfit for Eq.(12)is less than 2 and 1.6%for Eq.(13).

We adopted the pressure gradient as 0.034 GPa km-1from previous work(Matsui et al.2000)and the gravitational acceleration from PREM model;therefore,the temperature gradient can be calculated from Eq.(11).

The estimated temperature gradient is shown in Fig.6 along with the former results(Katsura et al.2010;Stacey and Davis 2008).Figure 7 illustrates the thermal expansion variation in the mantle.The gradient is～0.64 K km-1at the top of the asthenosphere, then decreases to～0.37 K km-1at the 410 km discontinuity.In Fig.7,the trend in our results generally agrees with that of Katsura et al.(2010)in concluding that the values decrease with increasing depth.The thermal expansion given by Stacey and Davis(2008)and Katsura et al.(2010),respectively,was for forsterite,which is Fe-free olivine,and the thermal expansion for San Carlos olivine is approximately 10%higher than that of forsterite,which might be caused by the content of Fe.

4 Conclusion

In this work,we used a numerical method,which was applied to liquids only,to calculate various parameters of San Carlos olivine.Matching the previous data of heat capacity and density at ambient pressure with sound velocities at high pressure,we derived the molar volume,adiabatic bulk modulus,and shear modulus as a function of temperature and pressure,and then we extrapolated the pressure range to about 14 GPa,which is the approximate pressure of the 410 km discontinuity.The calculated results agreed with the former experimental data and proved the feasibility of our theoretical method.Most importantly,our theoretical method can be used to determine the thermal expansion and heat capacity of minerals at high pressure,which are hard to measure through experimentation.We not only deduced a fitting equation of thermal expansion and heat capacity of San Carlos olivine as a function for both temperature and pressure,but alsoproposed the variations of heat capacity with increasing pressure∂CP/∂P=3.67×10-2P-1.43,which are useful for making decisions in a thermodynamic analysis.Finally,we presented the temperature gradient to the 410 km discontinuity using the thermodynamic parameters that we derived,which provided the variations of the thermodynamic properties in the mantle.

Table 2 Fitting coefficients for Eq.(12),P in GPa,T in K and α in K-1

Table 3 Fitting coefficients for Eq.(13),P in GPa,T in K and CPis in J kg-1K-1

Fig.6 Temperature gradient with increasing depth

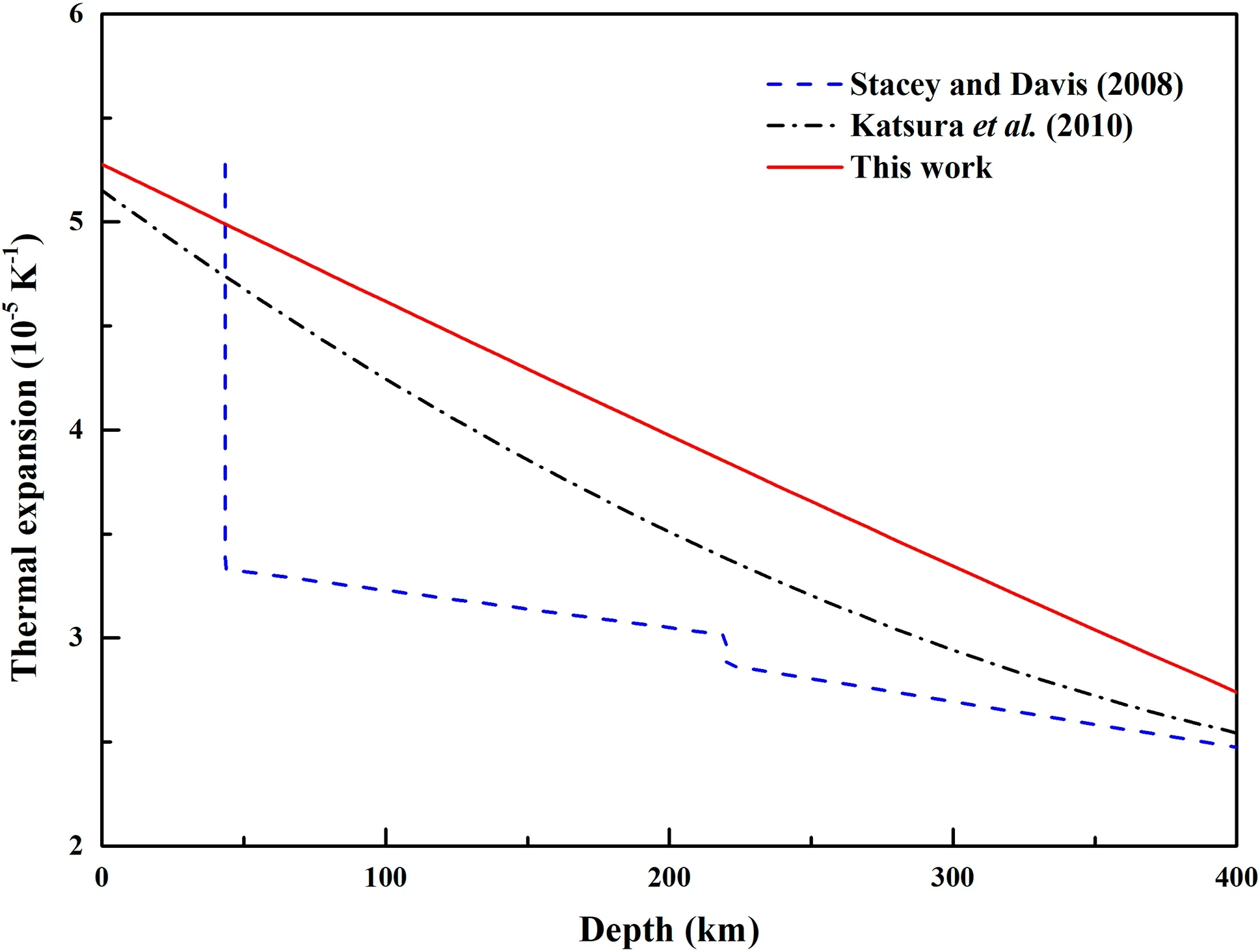
Fig.7 Thermal expansion variation of San Carlos olivine with increasing depth

AcknowledgementsThis work was supported by the Strategic Priority Research Program(B)of Chinese Academy of Sciences(XDB 18010401)and Light of the West Foundation of Chinese Academy of Sciences(Y5CR025000).

Abramson EH,Brown JM,Slutsky LJ,Zaug JM(1997)The elastic constants of San Carlos olivine to 17 GPa.J Geophys Res Solid Earth 102:12253–12263.https://doi.org/10.1029/97jb00682

Akaogi M,Ross NL,Mcmillan P,Navrotsky A(1984)The Mg2SiO4polymorphs(olivine,modified spinel and spinel):thermodynamic properties from oxide melt solution calorimetry,phase relations,and models of lattice vibrations.Am Miner 69:499–512

Akaogi M,Takayama H,Kojitani H,Kawaji H,Atake T(2007)Lowtemperature heat capacities,entropies and enthalpies of Mg2SiO4polymorphs,and alpha-beta-gamma and post-spinel phase relations at high pressure.Phys Chem Miner 34:169–183.https://doi.org/10.1007/s00269-006-0137-3

Anderson OL(1966)Derivation of wachtman’s equation for temperature dependence of elastic moduli of oxide compounds.Phys Rev 144:553.https://doi.org/10.1103/PhysRev.144.553

Anderson OL(1967)Equation for thermal expansivity in planetary interiors.J Geophys Res72:3661.https://doi.org/10.1029/JZ072i014p03661

Andersson SP,Ross RG(1994)Thermal conductivity and heatcapacity per unit volume of poly(methyl methacrylate)under high pressure.Int J Thermophys 15:949–962.https://doi.org/10.1007/Bf01447105

Ashida T,Kume S,Ito E(1987)Thermodynamic aspects of phase boundary among α-, β-,and γ-Mg2SiO4.In:Manghnani MH,Syono Y(eds)High pressure research in mineral physics.Terra Scientific Publishing,Tokyo/American Geophysical Union,Washington

Ayrinhac S et al(2014)Equation of state of liquid mercury to 520 K and 7 GPa from acoustic velocity measurements.J Chem Phys 140:244201.https://doi.org/10.1063/1.4882695

Ayrinhac S,Gauthier M,Le Marchand G,Morand M,Bergame F,Decremps F(2015)Thermodynamic properties of liquid gallium from picosecond acoustic velocity measurements.J Phys:Condens Matter 27:275103.https://doi.org/10.1088/0953-8984/27/27/275103

Barin I,Knacke O,Kubaschewski O (1973)Thermochemical properties of inorganic substances.Springer,Berlin

Berman RG,Brown TH(1985)Heat capacity of minerals in the system Na2O–K2O–CaO–MgO–FeO–Fe2O3–Al2O3–SiO2–TiO2–H2O–CO2:representation,estimation,and high temperature extrapolation.Contrib Mineral Petrol 89:168–183.https://doi.org/10.1007/Bf00379451

Chen G,Li B,Liebermann RC(1996)Selected elastic moduli of single-crystal olivines from ultrasonic experiments to mantle pressures.Science 272:979–980.https://doi.org/10.1126/science.272.5264.979

Chorazewski M,Dzida M,Zorebski E,Zorebski M(2013)Density,speed of sound,heat capacity,and related properties of 1-hexanol and 2-ethyl-1-butanol as function of temperature and pressure.J Chem Thermodyn 58:389–397.https://doi.org/10.1016/j.jct.2012.09.027

Darling KL,Gwanmesia GD,Kung J,Li BS,Liebermann RC(2004)Ultrasonic measurements of the sound velocities in polycrystalline San Carlos olivine in multi-anvil,high-pressure apparatus.Phys Earth Planet Inter 143:19–31.https://doi.org/10.1016/j.pepi.2003.07.018

Davis LA,Gordon RB(1967)Compression of mercury at high pressure.J Chem Phys46:2650.https://doi.org/10.1063/1.1841095

de Koker N(2012)Melting of cubic boron nitride at extreme pressures.J Phys:Condens Matter 24:055401.https://doi.org/10.1088/0953-8984/24/5/055401

Fei YW(1995)Mineral physics and crystallography:a handbook of physical constants.American Geophysical Union,Washington

Frey FA,Prinz M(1978)Ultramafic inclusions from San Carlos,Arizona:petrologic and geochemical data bearing on their petrogenesis.Earth Planet Sci Lett 38:129–176.https://doi.org/10.1016/0012-821x(78)90130-9

Hashimoto M,Tomioka F,Umehara I,Fujiwara T,Hedo M,Uwatoko Y(2006)Heat capacity measurement of CePd2Si2under high pressure.Phys B 378–80:815–816.https://doi.org/10.1016/j.physb.2006.01.298

Isaak DG(1992)High-temperature elasticity of iron-bearing olivines.J Geophys Res Solid Earth 97:1871–1885.https://doi.org/10.1029/91jb02675

Jacobs MHG,Schmid-Fetzer R,van den Berg AP(2017)Phase diagrams,thermodynamic properties and sound velocities derived from a multiple Einstein method using vibrational densities of states:an application to MgO–SiO2.Phys Chem Miner 44:43–62.https://doi.org/10.1007/s00269-016-0835-4

Jianping L,Kornprobst J,Vielzeuf D,Fabriès J(1995)An improved experimental calibration of the olivine-spinel geothermometer Chinese. J Geochem 14:68–77. https://doi.org/10.1007/bf02840385

Katsura T,Yoneda A,Yamazaki D,Yoshino T,Ito E(2010)Adiabatic temperature profile in the mantle.Phys Earth Planet Inter 183:212–218.https://doi.org/10.1016/j.pepi.2010.07.001

Kojitani H,Inoue T,Akaogi M(2016)Precise measurements of enthalpy of postspinel transition in Mg2SiO4and application to the phase boundary calculation.J Geophys Res Solid Earth 121:729–742.https://doi.org/10.1002/2015jb012211

Li B,Ge J,Zhang B(2017)Diffusion in garnet:a review.Acta Geochim.https://doi.org/10.1007/s11631-017-0187-x

Liu W,Li BS(2006)Thermal equation of state of(Mg0.9Fe0.1)2SiO4olivine.Phys Earth Planet Inter 157:188–195.https://doi.org/10.1016/j.pepi.2006.04.003

Liu W,Kung J,Li BS(2005)Elasticity of San Carlos olivine to 8 GPa and 1073 K.Geophys Res Lett 32:4.https://doi.org/10.1029/2005gl023453

Mao Z,Fan DW,Lin JF,Yang J,Tkachev SN,Zhuravlev K,Prakapenka VB(2015)Elasticity of single-crystal olivine at high pressures and temperatures.Earth Planet Sci Lett 426:204–215.https://doi.org/10.1016/j.epsl.2015.06.045

Matsui M,Parker SC,Leslie M(2000)The MD simulation of the equation of state of MgO:application as a pressure calibration standard at high temperature and high pressure.Am Miner 85:312–316.https://doi.org/10.2138/am-2000-2-308

Navrotsky A(1995)Thermodynamic properties of minerals.In:Mineral physics&crystallography:a handbook of physical constants.American Geophysical Union,pp 18–28.https://doi.org/10.1029/rf002p0018

Nesbitt HW,Bancroft GM,Henderson GS,Richet P,O’Shaughnessy C(2017)Melting,crystallization,and the glass transition:toward a unified description for silicate phase transitions.Am Miner 102:412–420.https://doi.org/10.2138/am-2017-5852

Osako M,Ito E,Yoneda A(2004)Simultaneous measurements of thermal conductivity and thermal diffusivity for garnet and olivine under high pressure. Phys Earth Planet Inter 143:311–320.https://doi.org/10.1016/j.pepi.2003.10.010

Price GD,Parker SC,Leslie M(1987)The lattice dynamics and thermodynamics of the Mg2SiO4polymorphs.Phys Chem Miner 15:181–190.https://doi.org/10.1007/Bf00308782

Richet P(1987)Heat capacity of silicate glasses.Chem Geol 62:111–124.https://doi.org/10.1016/0009-2541(87)90062-3

Robie RA,Hemingway BS,Takei H(1982)Heat capacities and entropies of Mg2SiO4,Mn2SiO4,and Co2SiO4between 5 K and 380 K.Am Miner 67:470–482

Stacey F,Davis P(2008)Physics of the earth.Cambridge University Press,Cambridge

Su C,Liu YG,Wang ZG,Song W,Asimow PD,Tang HF,Xie HS(2017)Equation of state of liquid bismuth and its melting curve from ultrasonic investigation athigh pressure.Phys B 524:154–162.https://doi.org/10.1016/j.physb.2017.08.049

Suzuki I(1975)Thermal expansion of periclase and olivine,and their anharmonic properties.In:Elastic properties and equations of state.American Geophysical Union,pp 361–375.https://doi.org/10.1029/sp026p0361

Watanabe H(1982)Thermochemical properties of synthetic highpressure compounds relevant to the earth’s mantle.High pressure research in geophysics.Center for Academic Publications Japan,Tokyo

Webb SL(1989)The elasticity of the upper mantle orthosilicates olivine and garnet to 3 GPa.Phys Chem Miner 16:684–692

Yoneda A,Osako M,Ito E(2009)Heat capacity measurement under high pressure:a finite element method assessment.Phys Earth Planet Inter 174:309–314.https://doi.org/10.1016/j.pepi.2008.10.004

Zha CS,Duffy TS,Downs RT,Mao HK,Hemley RJ(1998)Brillouin scattering and X-ray diffraction of San Carlos olivine:direct pressure determination to 32 GPa.Earth Planet Sci Lett 159:25–33.https://doi.org/10.1016/S0012-821x(98)00063-6

Zhang JS,Bass JD(2016)Sound velocities of olivine at high pressures and temperatures and the composition of Earth’s upper mantle.Geophys Res Lett 43:9611–9618.https://doi.org/10.1002/2016gl069949