基于克里金插值的自适应VIRE室内定位算法研究
2018-06-26顾军华董永峰白振东
顾军华 ,许 鹏 ,董 瑶,董永峰,白振东
1.河北工业大学 计算机科学与软件学院,天津 300401
2.河北工业大学 电子信息工程学院,天津 300401
3.河北省大数据计算重点实验室,天津 300401
1 引言
随着普适计算的不断深入和发展,基于位置信息的服务越来越受到人们的关注,基于RFID、802.11b、蓝牙、超宽带等技术的定位系统相继被提出[1-3]。现有的RFID定位算法大多是基于信号强度指示(Received Signal Strength Indicator,RSSI)来估计待定位物体的位置[4],比较经典的算法有LANDMARC[5]和VIRE[6]。LANDMARC采用了充当定位参考点的参考标签辅助定位,VIRE在此基础上引入了虚拟参考标签,减小了参考标签间的相互干扰[7-8],提高了定位准确性。但VIRE算法的缺点在于扩充参考标签的RSSI数据集时采用的是线性插值,而RSSI与距离之间并非线性关系[9],并且虚拟标签消除过程中的阈值参数需要通过反复调整实验获得,此方法过于复杂,当应用场景环境变化较大时,固定的阈值便会失效,导致误差增大。
针对上述问题,本文提出一种对VIRE算法的改进算法——基于克里金插值的自适应VIRE算法。本文算法采用一种基于统计学方式计算的克里金插值法估计虚拟标签[10-11]。采用变异函数为高斯模型的克里金插值法,不仅考虑待估计位置数据与已知位置数据的相互关系,而且还考虑变量的空间相关性,更准确估计虚拟标签数据。本文算法还提出一种自适应阈值调整策略,通过预先估计虚拟标签消除后邻近标签个数的范围,逐步调整阈值大小,使邻近标签数量保持在最佳状态,更准确排除干扰。最后通过对比实验验证本文提出的基于克里金插值的自适应VIRE算法更具有优越性。
2 VIRE算法简介
VIRE算法由经典的LANDMARC算法改进而来,采用了充当定位参考的参考标签辅助定位,并通过线性插值法扩充参考标签密度,之后消除不可能的位置,由剩下的“邻近标签”[12]加权平均来校正待定位标签的不确定性,使得算法在定位过程中受外界环境变化的影响较小,具有较高的稳定性。VIRE具体实现如下:
在定位区域按长方形网格状铺设已知位置信息的参考标签,将每4个实参考标签所覆盖的标签网格单元进一步分成N×N(N为虚拟标签密度)的等大虚拟网格单元,每个虚拟网格端点看成一个虚拟标签。实参考标签的RSSI通过阅读器测得,坐标为已知量。设某一坐标(i,j)(i,j∈R)落在参考标签网络中,四周有4个实参考标签所围绕,实参考标签的RSSI通过阅读器获得,通过线性插值在已知的实参考标签的基础上计算出该区域的虚拟标签的坐标和RSSI。虚拟参考标签在水平方向和垂直方向上的RSSI由式(1)和式(2)求出。
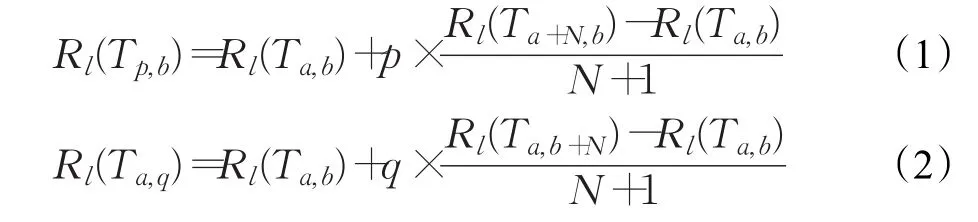
其中 p=i%N(0≤p≤N-1)为待估计虚拟参考标签与已知起始标签在X轴的间隔,q=j%N(0≤q≤N-1)为待估计虚拟参考标签与已知起始标签在Y轴的间隔;参数 a=ëi/Nû,b=ëj/Nû,ë û表示向下取整。
虚拟标签网格建立后对应的可得到第l个阅读器读取的参考标签信号强度矩阵Sl,将该矩阵每个元素与第l个阅读器读取的待定位标签信号强度θl做差,如结果在特定阈值以下,记1,反之记0,得到的矩阵称为邻近图(proximity map)[6]。取全部L个邻近图的交集为待定位标签所在的可能性最大的区域。引入两个权重因子ω1i、ω2i。

其中Rl(Ti)是第l个阅读器得到第i个虚拟参考标签的RSSI值,Rl(θ)是第l个阅读器读取待定位标签的RSSI。

将连接在一起的标签位聚为一类,nci是第i类中的标签数,na是聚类后的类数,得到权值ω2i。ωi=ω1i×ω2i作为最终权值,得待定位标签坐标为:

3 基于克里金插值的自适应VIRE算法
3.1 基于克里金插值的虚拟标签计算
克里金(Kriging)插值法[10-11]是建立在变异函数理论分析基础上,对有限区域内的变量取值进行最优线性无偏估计的一种方法。克里金法不仅考虑待估计位置数据与已知位置数据的相互关系,而且还考虑变量的空间相关性,试用克里金插值法计算虚拟参考标签RSSI。
设Xi是定位区域中第i(1≤i≤M)个参考标签位置,各标签特征属性RSSI为R(Xi),那么,虚拟标签点X0的RSSI值的无偏估计可用下式表示:

λi为该实参考标签对插值点的权重。普通克里金插值的权重系数由以下两个方程决定:
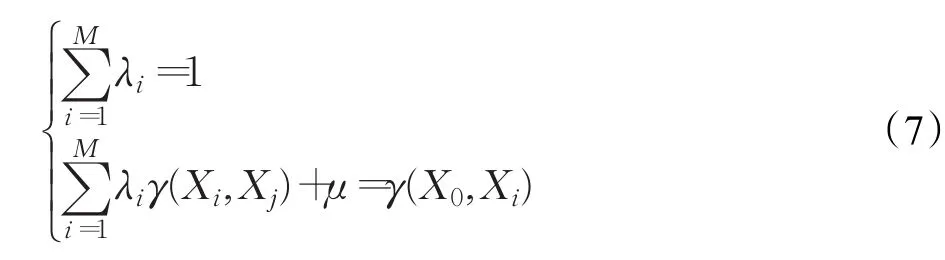

式中,C0为块金常数,C为拱高,变程h=当C0=0,C=1时,称为标准高斯模型。
通过上式求得各变异函数值γ(h)代入方程组(7),可得拉格朗日乘数μ和加权系数λi,再代入式(6)可得虚拟标签点X0的RSSI估计值。
式中γ(Xi,Xj)是R(X0)在实参考标签Xi和Xj之间的半方差[11],γ(X0,Xi)是R(X0)在实参考标签点Xi和虚拟标签点X0和之间的半方差,这些量都从适宜的变异函数计算得到。μ是极小化处理时的拉格朗日乘数。在内插计算过程中,为减少计算量,通常采用理论模型来拟合变异函数,拟合模型分为球型模型、环状模型、指数模型和高斯模型。高斯模型更符合标签RSSI与距离的关系,在这里采用高斯模型:
3.2 自适应阈值调整策略
阈值S作为VIRE算法中一个至关重要的参数,本文提出一种自适应阈值调整策略,步骤如下:
(1)估计虚拟参考标签消除过程后邻近标签数量nV的范围是最大邻近标签数,L是定位区域的阅读器数量,M为实参考标签总数,V为虚拟参考标签总数,最小邻近标签数取最大邻近标签数的0.3倍。
(2)遍历虚拟标签矩阵,找到L个阅读器读取到待定位标签的L个RSSI值与虚拟标签矩阵中的RSSI值的最大差值,最大差值作为初始阈值S。
(3)进行虚拟参考标签消除过程,统计最终邻近图中剩余的邻近标签数量nV。
(4)判断nV是否满足邻近标签数量范围,如果nV>Nmax,则减小阈值返回第(3)步;如果nV<0.3⋅Nmax,则增大阈值,返回第(3)步。
(5)如果满足邻近标签数量范围0.3⋅Nmax 算法流程如图1所示。 基于克里金插值的自适应VIRE室内定位算法流程如下: (1)获取实参考标签RSSI矩阵。 (2)利用克里金插值扩充矩阵以获得大量虚拟参考标签。 (3)采用虚拟标签RSSI与待定位标签的最大差值作为初始阈值,通过本文提出的自适应阈值调整策略迭代计算最佳阈值。 (4)当取得最佳阈值的同时也获得了对应邻近标签的集合,最后计算邻近标签权重因子,待定位标签的估计坐标即为所有邻近标签坐标的加权和。 本文采用探感物联公司生产的433 MHz有源RFID设备进行实验,阅读器采用R701型全向天线阅读器,标签采用T702型有源标签,有源标签由于自身携带电源,可主动向阅读器发信,并且在室内环境下有效读取半径可达50 m。 模拟搭建办公室实验环境,定位区域为4.5 m×4.5 m,将4个阅读器置于区域四角,16个标签放置成4×4阵列作为参考标签,实验测试了50个待定位,选取9个有代表性的待定位标签做详细说明,如图2所示。阅读器将采集的RSSI和标签序号等数据通过局域网传输到负责数据处理的PC端,算法通过Matlab软件编程实现。 为验证基于克里金插值的自适应VIRE算法的优越性,设计对比实验,实验选取经典VIRE算法、基于牛顿插值的VIRE算法与本文算法做对比。若待定位标签的真实坐标为(x0,y0),进行定位计算得到的坐标为(x',y'),则定义误差来描述算法性能。 经典的多项式插值法主要有拉格朗日插值、牛顿插值等。由插值多项式的存在唯一性定理可知,实际上这两种插值法式同一种方法的两种变形,其构造拟合函数的思路是相同的,两者计算结果也相同[13-14]。拉格朗日插值计算过程中增加一个节点时需要重新计算全部基函数,而牛顿插值法具有继承性,在插值节点增加后,只需在原有基础上计算均差表中新的一行即可,且插值余项也较容易,所以实验中对比的基于多项式插值的改进算法中选择了基于牛顿插值法的VIRE算法。 由于阅读器采集到的标签RSSI数据受多径效应的影响而存在波动,为此,每个待定位标签位置采集150次数据,进行高斯滤波处理,计算该组数据的均值μ和方差σ,公式如下: 构建高斯概率密度函数,遍历RSSI数据,选择概率密度值大于最大值0.6倍的数据存入新的数组,如式(11),取新数组的算术平均值为该待定位标签的RSSI值。 为测试不同插值方法对VIRE算法定位精度的影响,设计实验一,分别选取线性插值、牛顿插值、克里金插值作为VIRE算法的插值方法,阈值均为9,同时测试虚拟标签密度对定位精度的影响。虚拟标签密度定义为任意两个实参考标签之间新增的虚拟标签数,设虚拟标签密度从1到9变化,记录三种算法在不同插值密度下的平均定位误差,实验结果如图3所示。 图3 不同插值法和插值密度下对定位精度的影响 从图3可以看出三种算法的平均定位误差随虚拟标签密度值从1到9增大时均呈现下降趋势,当虚拟标签密度参数取值大于4时,采用三种插值方法的算法的平均定位误差都趋于稳定不再降低,此时继续增加虚拟标签密度会使算法时间复杂度迅速上升,但定位精度也不再提高。可以看出本文采用克里金插值的算法平均定位误差随着虚拟标签密度的增大下降的最快,稳定后的平均定位误差最小,为0.81 m,并且在同等定位精度的前提下,克里金插值法所需标签数最小,减少了定位成本。 阈值作为VIRE算法的重要参数,其值的选取直接关系定位精度的高低。现通过实验设阈值取0至40之间的整数,分别测试50个点的待定位标签,记录不同待定位标签的定位误差随阈值变化的曲线,随机选取标签A、B、C的结果如图4所示。 可从图4的实验结果中找到不同标签的最佳阈值,需要注意的是,这样找出最佳阈值的前提是在已知待定位标签位置的情况下进行的,是为了评价本文提出的自适应阈值调整策略的计算结果,但实际定位过程中无法计算定位误差,因此,采用经典VIRE算法也就无法获得最佳阈值。为此,本文提出自适应阈值调整策略以期估计最佳阈值。 图4 测试标签定位误差随阈值的变化 为测试自适应阈值调整策略找到恰当阈值的所需时间和结果,采用自适应阈值调整策略,测试同一组50个待定位标签的数据,记录自适应迭代次数和阈值计算结果。标签A、B、C采用自适应阈值的计算结果如图5所示。 图5 测试标签阈值随自适应迭代次数的变化 可以看出标签阈值在迭代初期下降较快,在接近迭代停止条件时下降速度变缓,最终满足停止条件,获得最佳阈值。其中标签A、B在第6代时结束计算,标签C在第7代时结束,不同标签的自适应阈值调整迭代次数和阈值不尽相同。 从图4对应的实验中提取标签最佳阈值情况下和自适应阈值调整后对应的平均定位误差,从图5对应的实验中提取待定位标签自适应阈值调整的结果,如表1所示。自适应阈值调整后的定位误差在一定程度上逼近了最佳阈值情况下的计算结果。 表1 最佳阈值下与自适应阈值下定位误差对比 为验证本文算法的性能,设计实验三,分别测试本文提出的基于克里金插值的自适应VIRE算法、经典VIRE算法和基于牛顿插值的VIRE算法在相同实验环境下的平均定位误差。其中经典VIRE算法和基于牛顿插值的VIRE算法的阈值经实验设定为9。图2中标注的9个有代表性位置的标签误差计算结果如图6所示。 图6 不同定位算法定位误差 从图6可以看出采用本文算法估计的待定位标签平均定位误差最小。在全部50个待定位标签中,VIRE算法的平均定位误差为0.897 6 m,基于牛顿插值的VIRE算法的平均误差为0.811 2 m,基于克里金插值的自适应VIRE算法的平均定位误差为0.647 3 m,较前两者分别降低了27.88%和20.20%。 将实验结果按不同定位误差所占比重划分,得到三种算法的定位误差累计分布如图7所示,自变量为最大定位误差限,因变量的含义为待定位标签定位误差小于对应的自变量定位误差限的数量所占全部测试标签数量的比例。 图7 不同算法的定位误差累计分布 从图7可以看出,采用本文算法的实验结果中有49%的标签定位误差小于0.6 m,全部标签的定位误差控制在1 m以内;采用基于牛顿插值法改进的VIRE算法中有30%的标签定位误差小于0.6 m,最差定位误差在1.2 m以内,采用经典VIRE算法计算的标签中仅有14%的定位误差小于0.6 m,最差定位误差为1.4 m。从结果中可以看出本文算法提高了定位结果的精度和稳定性。 本文在VIRE算法的基础上进行改进,提出一种基于克里金插值的自适应VIRE算法,通过实验验证了采用克里金插值法计算虚拟参考标签的RSSI相比采用线性插值和牛顿插值的定位误差更小,并且提出的自适应阈值调整策略在一定程度上逼近了最佳阈值情况下的计算结果。改进后的算法可以在不增加参考标签数量的情况下,进一步提高定位精度和定位结果的稳定性,节省了成本。 [1]Zhang Y J,Chen E X.An approximate sphere of the four anchor nodes positioning method based on RSSI[J].Sensors&Transducers,2015,186(3):85-92. [2]Li N,Becerik-Gerber B.Performance-based evaluation of RFID-based indoor location sensing solutions for the built environment[J].Advanced Engineering Informatics,2011,25(3):535-546. [3]Jiang X,Liu Y,Wang X.An enhanced approach of indoor location sensing using active RFID[C]//WASE International Conference on Information Engineering,2009,1:169-172. [4]Zhao Y,Hong W,Cheung S C.The impact of reader to tag collision on RFID tag identification[C]//International Conference on Wireless Algorithms,Systems,and Applications.Berlin,Germany:Springer,2010:115-119. [5]Ni L M,Liu Y,Lau Y C,et al.LANDMARC:Indoor location sensing using activeRFID[J].WirelessNetworks,2004,10(6):701-710. [6]Zhao Y,Liu Y,Ni L M.VIRE:Active RFID-based localization using virtual reference elimination[C]//2007 International Conference on Parallel Processing,2007:56. [7]姜丽芬,卢桂章,辛运帏.射频识别系统中的防碰撞算法研究[J].计算机工程与应用,2007,43(15):29-32. [8]Ahn H S,Yu W.Environmental-adaptive RSSI-based indoor localization[J].IEEE Transactions on Automation Science and Engineering,2009,6(4):626-633. [9]周彦,文宝,李建勋.无线传感器网络节点近点加权质心定位方法[J].计算机工程与应用,2012,48(1):87-89. [10]徐爱萍,胡力,舒红.空间克里金插值的时空扩展与实现[J].计算机应用,2011,31(1):273-276. [11]李方,王铁成,佟为明.基于空间变异理论的电子地图构建方法[J].哈尔滨工程大学学报,2012(6):715-719. [12]王远哲,毛陆虹,刘辉,等.基于参考标签的射频识别定位算法研究与应用[J].通信学报,2010,31(2):86-92. [13]李庆扬,王能超,易大易.数值分析[M].5版.北京:清华大学出版社,2010:23-35. [14]徐杨杰,王艳,严大虎,等.基于Newton插值与混合灰狼优化SVR的RFID定位算法[J].系统仿真学报,2017,29(9):1921-192.3.3 改进后的算法流程
4 实验环境构建
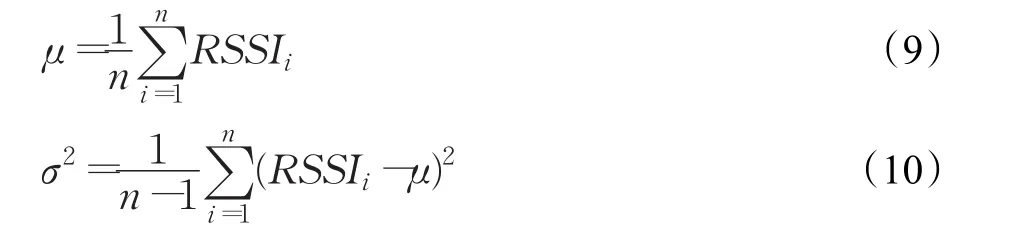
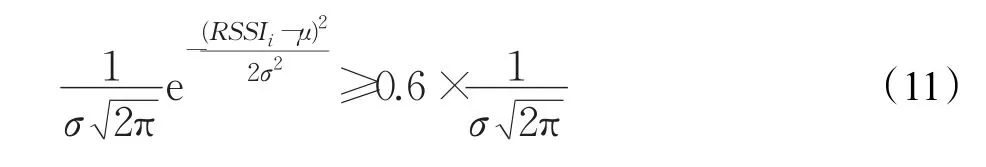
5 实验结果对比分析
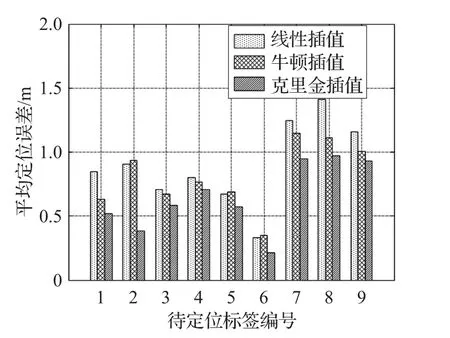
5.1 不同插值方法和插值密度对比实验
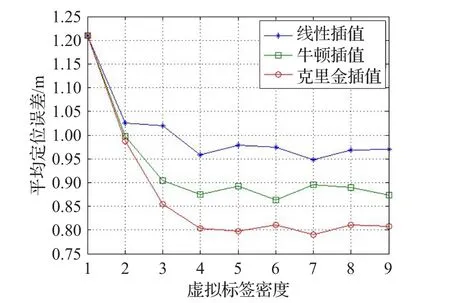
5.2 自适应阈值调整策略实验
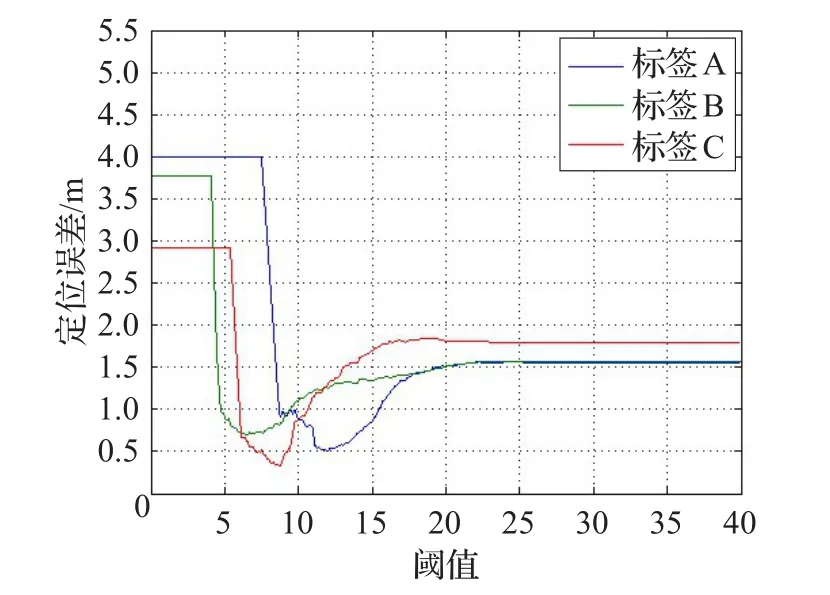
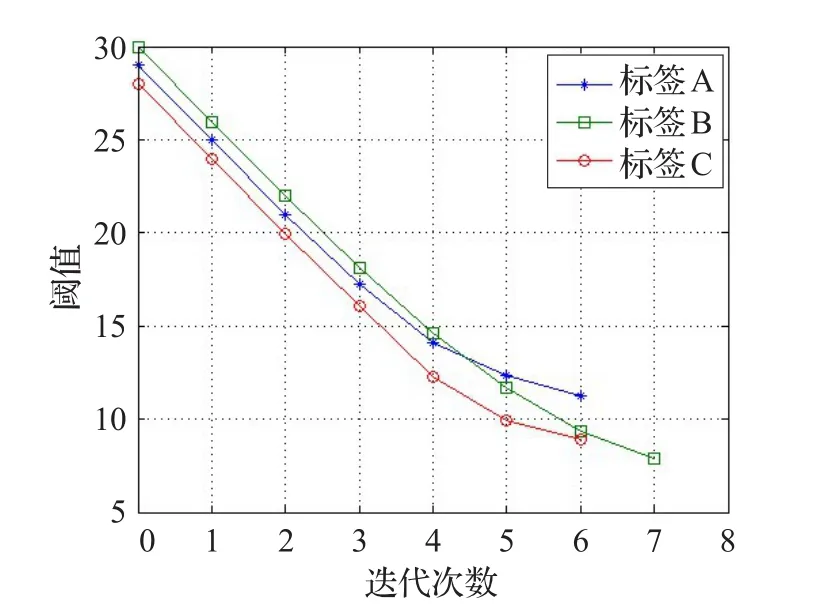
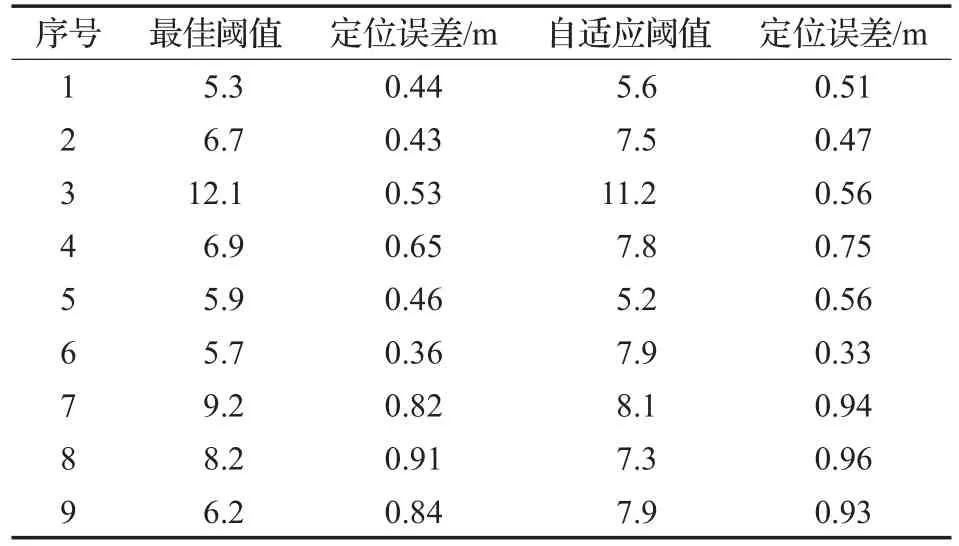
5.3 基于克里金插值的自适应VIRE算法性能试验
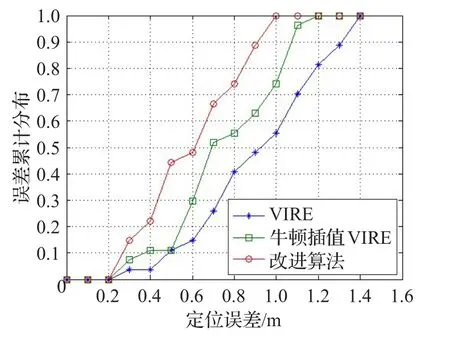
6 结束语
