基于量子遗传算法的圆度误差测量研究

申翠香， 张晓宇

(1.三门峡市卫生学校， 河南 三门峡 472143； 2.河南有线电视网络集团 三门峡分公司， 河南 三门峡 472000)

1 前 言

圆度误差是评定轴、孔等回转体零件的重要指标，随着工业市场发展的需求，对圆度的测量要求越来越严格[1]。 采用影像测量法对圆度误差测量[2]，适合测量刃口形的小型件，效率比较高，但是实际测量由操作人员的熟练程度等因素决定；转轴式和转台式圆度仪测量圆度，精度较高[3]，但是对测量环境要求较高；Hough变换检测圆度[4]，由于变换复杂需要较多的计算时间，测量效率较低；三点法、两点法测量圆度方法较简单[5，6]，但是只适用于圆度低精度测量。最小二乘法简便易行，但不满足最小条件的圆度误差评定准则，给实际测量带来了不便。

为了提高圆度测量精度，本文把最小二乘法和量子遗传算法进行结合。实验仿真显示本文算法获得了精确的测量数值，测量最大误差均在0.01%以内，同时最大误差波动比较平稳。

2 圆度特征获取

2.1 圆心与半径计算

从圆形最左方点L开始顺时针获取相隔距离为m的点M，连接LM，再取与点M相隔距离也为m的点N，连接MN，从而获得线段LM、MN，同时LM=MN；同理获得ES、ST。LM、MN、ES、ST的垂直平分线交汇于圆心点O，如图1所示。

图1 圆心获取过程

在图1中LM中点坐标为(x1,y1)：

(1)

式中:(xL,yL)、(xM,yM)为圆周上点L、点M的坐标。同理可得MN中点坐标(x2,y2)，经过线段LM、MN中点的法线方程为

(2)

式中:(xN,yN)为点N的坐标；(x0,y0)为圆心点O的坐标。因此，线段LM、MN垂直平分线的交点在圆心O。在圆周上取2p条相似于LM的线段，并且求出垂直平分线的交点后[7，8]，统计各个累加交点峰值即可获得圆心O的坐标(x0,y0)，通过计算各点到圆心坐标距离的平均值获得检测圆度的半径r：

(3)

当测得多个采样点坐标Ω=(xi,yi)，i=1,2,…,N，通过y=f(x)来反映x、y之间函数关系，最佳地拟合圆周轮廓点集数据为

y=f(x)=c0+c1x+c2x2+…+cmxm

(4)

式中:cl(l=0,1,…,m)为拟合函数系数；m为拟合函数阶次。将坐标拟合构造出数学模型：

minf(x0,y0,r)=

(5)

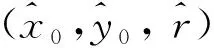
(6)

当均方误差ε最小即可获得最佳圆心，本文要求ε最小为0.015 6。

2.2 圆度计算

圆形复杂度的特征量圆度e为

(7)

式中:e∈[0,1]，值越大形状越接近于圆，A是圆度像素区域面积。

若e与圆度的标准值es满足：

|e-es|<0.1es

(8)

则认为当前检测是合格零件；否则将该检测作为不符合要求的零件进行剔除[10,11]。

3 基于量子遗传算法的圆度误差测量

3.1 多进制遗传编码

设量子个体Q(t)为第t代的量子个体[12]，其量子矩阵为

(9)

3.2 量子旋转门更新

量子遗传进化算法中[13]，通过量子旋转门更新系统:

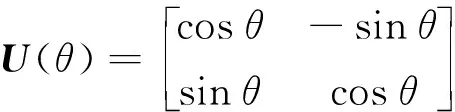
(10)

式中:θ为量子旋转角，其正负号决定算法收敛方向，其值决定算法收敛速度。

旋转角θ采用的策略为

(11)

式中:s(αi,βi)为控制第i个量子旋转角的方向，α是量子比特处于状态0的概率幅，β是处于状态1的概率幅；λ是正常数；Δθ是初始旋转角；fmax为当代染色体的最大适应度函数值；f(x)、f(b)分别为当前解和历史最优解的适应度函数值。调整的结果使得概率幅(αi,βi)始终向着最优解出现的方向旋转；δ为每次调整的步长，其取值影响收敛速度，公式为

(12)

式中:t为迭代次数；tmax为迭代最大次数。

3.3 检测过程

(1)输入圆度图像，初始化量子个体；

(2)Qi(t)量子旋转门操作更新；

(3)改变调整步长δ；

(4)量子处于状态1的概率大于0.998 1，执行步骤(5)，否则t=t+1，转向步骤(2)；

(6)计算圆度e，满足公式(8)标准圆度值，进行步骤(7)，否则再次按次品处理；

(7)输出圆度检测结果。

4 实验仿真

量子遗传算法参数为：最大迭代次数tmax=200，种群大小n= 20,初始旋转角Δθ=1°，转角变化率调整系数λ=6，多进制量子态遗传编码对应概率的下限μ=0.000 5、上限κ=0.95，圆度误差测量成功标准为最优解函数值与全局最优值之差小于0.000 1。通过MATLAB R2014b软件编程实现圆度图像处理和分析，获得圆心坐标和半径参数的检测。

4.1 测量数据误差分析

通过三坐标测量机获得测量原始数据，由于三坐标测量机对数据处理系统中的圆度误差评定结果具有权威性，因此把三坐标测量机测量数据作为测量标准。本文算法与三坐标测量机对6 mm的被测圆度分别进行10次测量，表1所示为两种方法的测量数据。

从表1中的数据可以计算得出:经过10次测量，用三坐标测量机测量时被测圆度的半径平均值为3.006 68，方差为0.029 565 841，均差为0.010 013 418；本文算法测量时该被测圆度的半径平均值为3.000 82，方差为0.002 848 703，均差为0.003 561 25。本文算法与三坐标测量机测量结果误差相差小于0.005 8 mm，半径相对误差小于0.19%。

表1 两种方法测量数据

以三坐标测量机测量数据为标准，本文算法与其他算法测量结果相差值如图2所示。

从图2可以看出,本文算法的测量结果与三坐标测量机测量标准数据的相差值比较小，较接近三坐标测量机测量数据,其他测试方法较标准数据相差比较大。

通过随机10次测量，其测量数据最大误差波动如图3所示。

从图3可知，量子遗传算法测量可获得比较精确的数值，测量最大误差均在0.01%以内，达到了IT5公差等级，同时最大误差波动比较平稳，证明了该算法的稳定性较好。

图2 测量结果相差值

图3 测量数据最大误差波动

4.2 测量不确定度

为了评价本文算法的测量精度及有效性，通过灰色评定理论测量不确定度，由一次累加生成序列和理想累加序列得到其最大差值Δmax，那么圆半径测量的不确定度s为

式中:c为灰色常系数，取值2.5；w为测试次数。不确定度越小，测量结果与实际值较接近；不确定度越大，测量结果较差。不同方法的测量不确定度如图4所示。

图4 不同方法的测量不确定度

从图4可知，本文量子遗传算法测量不确定度在0.074至0.075 μm之间，比其它方法值较低，测量精度较高。

5 结 论

本文采用量子遗传算法提高了圆度测量精度，测量最大误差均在0.01%以内，同时最大误差波动比较平稳，为圆度误差测量提供一种新的参考方法。

[参考文献]

[1] 王东霞,宋爱国,温秀兰. 微分进化算法在圆度误差评定中的应用[J].计量学报,2015, 36(2): 123-127.

[2] 吴新杰,王苗苗,黄国兴.基于粒子滤波和机器视觉的圆形零件尺寸测量[J].机械设计与制造,2012,(11):49-51.

[3] 宋康,廖俊必, 林长青,等.圆度仪的调平和圆柱度误差评定[J].光学精密工程,2014,22(12):3360-3367.

[4] de Souza G B, Marana A N.HTS and HTSn: New shape descriptors based on Hough transform statistics[J].ComputerVisionandImageUnderstanding,2014,127(10):43-56.

[5] 杨俊超,于大国,徐文凯,等.一孔截面测算多圆心法检测深孔轴线直线度[J].科学技术与工程,2015,15(34):172-176.

[6] 李帆,周芬芬，李兴林,等.精密轴承钢球圆度测量误差分离技术研究现状[J].轴承,2015,(6):50-55.

[7] 周勇亮,金燕,何萍,等.随机Hough变换圆检测累计加速算法[J].计算机辅助设计与图形学学报,2014,26(4): 574-580.

[8] 龚立雄,黄敏.基于改进Hough变换的圆形零件尺寸测量研究[J].现代制造工程,2014,(2):98-102.

[9] 王健全,田欣利,张保国,等.微纳尺寸零件曲率半径测量方法[J].解放军理工大学学报(自然科学版),2014,15(1):56-61.

[10] 刘长青,李军,席巍.基于机器视觉的零件在线分选系统研究[J].数字技术与应用,2012,(4):71-73.

[11] 刘庆民，张蕾，吴立群,等.基于机器视觉的非均匀分布点圆度误差评定[J].计量学报,2016, 37(6): 567-570.

[12] 沈微微,华明正,史洪玮.一种基于高校排课问题的新型量子遗传进化算法[J].现代电子技术,2013,36(20):7-10.

[13] 张磊,方洋旺,毛东辉,等.一种新的相位角编码量子进化算法[J].控制与决策,2015,30(4):739-744.