考虑软黏土率效应和强度软化的圆柱扩孔理想弹塑性解析解
2018-06-25田攀周航尹锋李建斌
田攀 ,周航 ,尹锋 ,李建斌
(1. 重庆大学 土木工程学院,重庆,400045;2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆,400045)
圆柱孔扩张理论自1972年VESIC[1]将其用于桩基承载力问题之后,便在岩土工程领域包括土体原位试验、隧道开挖、锚杆和桩基础承载力等实际问题中得到了广泛的应用[2]。BUTTERFIED等[3]提出了平面应变条件下的柱孔扩张理论;蒋明镜等[4]基于统一强度理论和体积平衡原理,研究了应变软化Tresca材料的扩孔问题;贾尚华等[5]研究了砂土中柱孔扩孔理论中的扩孔压力与扩孔半径分布分析;肖昭然等[6−7]研究了饱和土体中圆柱孔扩张问题的弹塑性解析解;邹金峰[8]基于塑性力学大变形理论,推导了柱孔和球孔扩张弹塑性解析解,并利用该解析解计算了饱和土体的劈裂灌浆压力;章定文等[9−11]研究了不同初始条件下的柱孔扩张弹塑性解析解。在实际工程问题中,常见的饱和软黏土土在扩孔作用下通常表现为Tresca材料特性[12]。EINAV等[13]分析桩体贯入试验中的贯入阻力发现:由于桩体刚度和周围土体刚度相差巨大,从而强大的挤压作用将会使桩周土体实际的应力应变关系与理想的Tresca应力应变关系有差别,呈现出时间效应;DAYAL等[14]根据拉伸试验得出土体的峰值强度比土体强度高5%~20%,呈现出应变率效应;梁发云等[15]研究了Tresca材料考虑应变软化特性的扩孔解析解。基于以上分析可知,虽然基于Tresca屈服准则的扩孔理论有很多,但是目前的解答均未考虑土体的率效应和土体强度软化作用,为此,本文作者提出一种考虑土体应变率和强度软化的扩孔理想弹塑性解。
1 理论模型的建立
1.1 基本假设
1)圆孔周围土体为各向同性的饱和土体,土体初始各向同性应力为σ0。
2)弹性区土体应力应变关系服从胡克定律。
3)柱孔扩张服从平面应变。
4)对于不排水的饱和黏土,在孔扩张过程中,土体的体积应变始终为0。
5)孔洞边界变化率均匀变化。
图1所示为无限饱和土体中柱孔扩张示意图。
1.2 方程的建立
1.2.1 塑性区应力
柱孔扩张理论下的应力平衡方程为

式中:σr和σθ分别为极坐标系下的径向应力以及切向应力;r为塑性区半径。
理想弹塑性Tresca屈服条件为

式中:su为不排水抗剪强度。
将式(2)代入式(1),平衡方程改写为
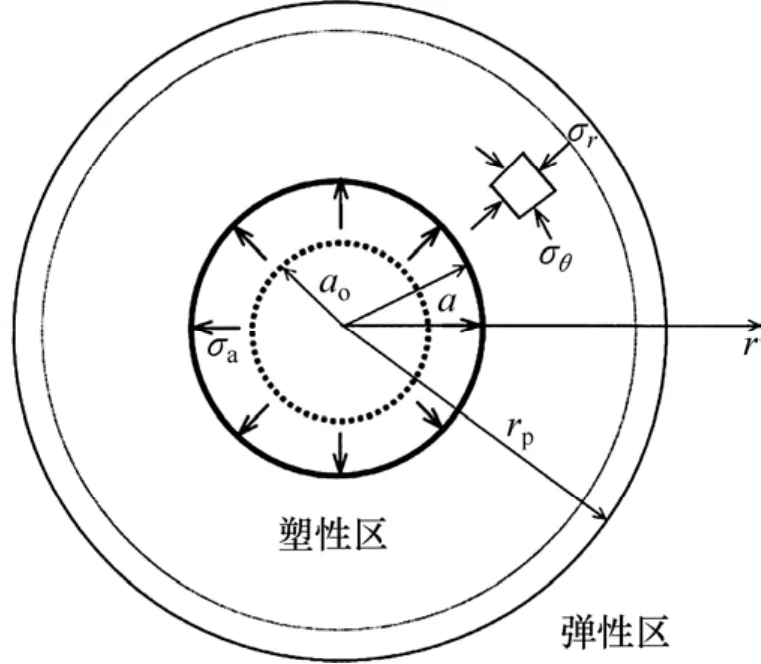
图1 柱孔扩张Fig. 1 Cylindrical cavity expansion

根据基本假定,在塑性区无体积变化,即

将式(4)两边同时对时间求导得

式中:r0为初始塑性区半径;a0和a分别为初始圆孔半径和扩孔后圆孔半径,ZHOU等[16]指出贯入仪器直径为初始圆孔直径,而贯入仪器直径为40~150 mm,故取初始圆孔直径a0=100 mm;和分别为径向坐标的变化率和孔洞边界的变化率,取
在塑性区的环向应变同时符合指数原则:

将式(4)和(5)代入式(6)得

EINAV等[13]指出土体抗剪强度会受到土体应变率和土体强度退化的影响,存在如下关系:

式中:ξ为在高斯点处的累积塑性剪应变;su0为初始剪切强度;μ为应变率系数,且BISCONTIN等[17]指出μ为0.05~0.30;为最大剪应变率的绝对值;为参考点剪切应变率;ξ95和δrem为强度软化系数,其中δrem为土体灵敏度的倒数;ξ95为土体强度退化到95%的累积塑性剪应变。
累积塑性剪应变ξ为

由于孔扩张过程中土体不排水(体应变为0),从而有εr=-εθ,因此,ξ可以写成

将式(4)和(6)代入式(10)得
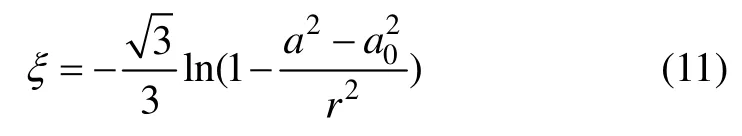
在弹塑性交界处塑性剪应变ξb为

由式(12)可得:塑性区半径rb为

另外,最大剪切应变率同样存在如下关系:

将式(7)代入式(14)化简得
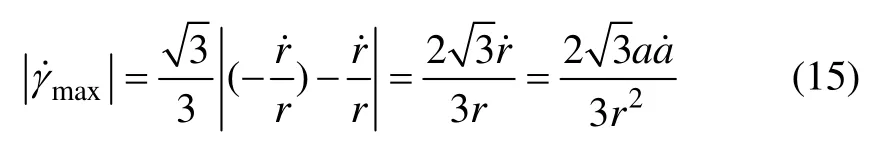
将式(11)和(15)代入式(8),su可改写为

当r=rb时,将式(13)代入式(16)得弹塑性交界处su,b为
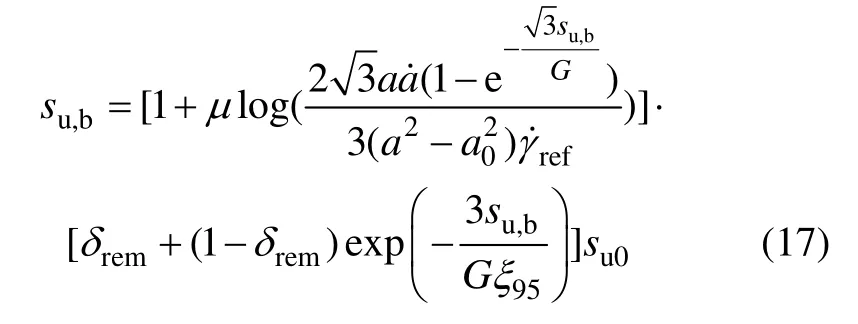
由式(17)可以确定弹塑性区交界处土体强度su,b,从而根据方程(13)可以确定塑性区半径。
将式(16)代入式(3)后,积分变形可得
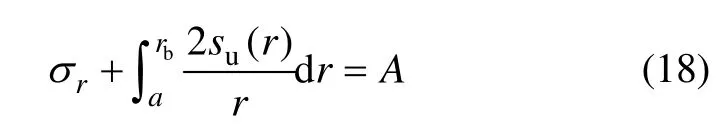
式中:i为正整数;A为常数。
当r=a时,由式(18)可得扩孔后的孔壁压力σa为
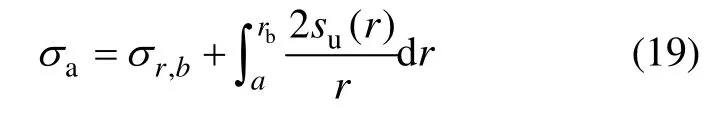
将方程(16)代入方程(19),可得σa:

式(20)可以通过数值积分获得解答。
由式(2)和(18)可得塑性区应力分布:

式中:a≤r≤rb。
式(21)和(22)同样可以通过数值积分获得解答。
1.2.2 弹性区应力
根据 CARTER等[18]对于不排水的饱和黏土中的扩张理论,其弹性解为:

2 理论模型的验证
SHUTTLE[19]基于 Tresca屈服准则提出了一种理想柱孔扩张弹塑性解,为了验证本文解的正确性,取μ=0,δrem=1,即在不考虑应变率和强度软化下,本文解与Shuttle解对比结果如图2和图3所示。从图2和图3可知:在不考虑应变率和强度软化情况下,本文孔壁正应力以及应力沿径向分布解析解与 Shuttle解相吻合,验证了本文解的合理性。
从图 2可以看出:当μ=0.3,δrem=0.2,ξ95=50,G/su0=330,即考虑应变率和强度软化影响时,由于受应变的影响,归一化的柱孔孔壁压力比未考虑时的要大,且孔壁压力随着扩孔半径的增加,孔壁压力可分为快速变化区、缓变区和衰减区3个区域:当扩孔半径小于1.5倍初始半径时,孔壁压力处于快速变化区,当扩孔半径超过 2.5倍初始半径时,由于受强度软化参数的影响,孔壁压力处于衰减区,其余区域属于缓变区,其孔壁压力随着扩孔半径的增加缓慢变化。从图3还可得到:离孔壁越远,径向应力越小,切向应力先减小后增加再减小,在塑性区其应力方向会发生改变,考虑应变率和强度软化时的弹塑性分界位置位于未考虑应变率和强度软化的左侧,说明考虑应变率和强度衰减后,其塑性区范围将会减小,同时在塑性区范围内,其径向应力和切向应力的强度变化率较未考虑时的要大。而在弹性区,考虑应变率和强度软化的曲线与未考虑时的重合。由以上分析可知:土体应变和强度软化将会影响扩孔理想弹塑性解析解。
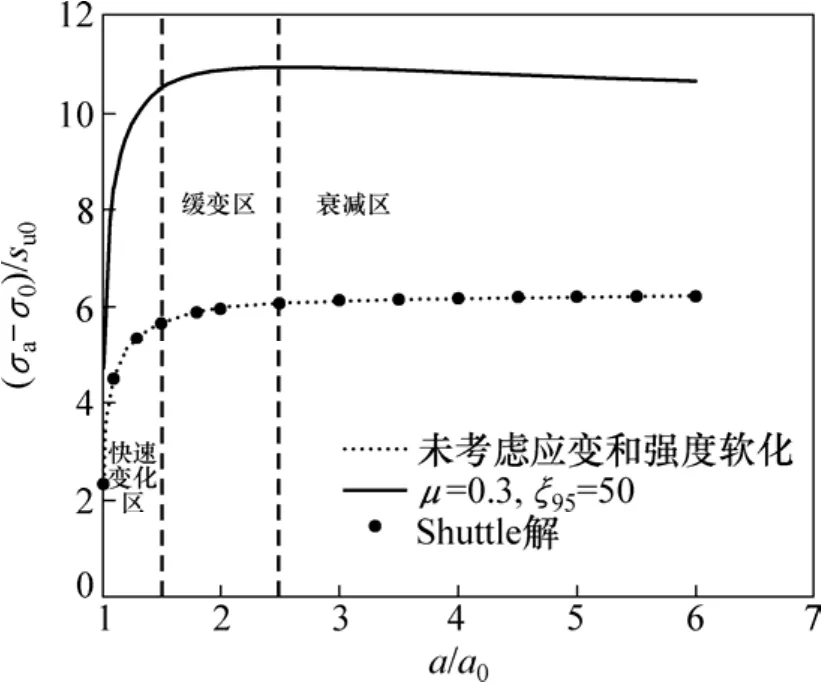
图2 归一化的孔壁压力随着扩孔半径的变化Fig. 2 Variation of normalized cylindrical cavity pressure with cavity expansion radial
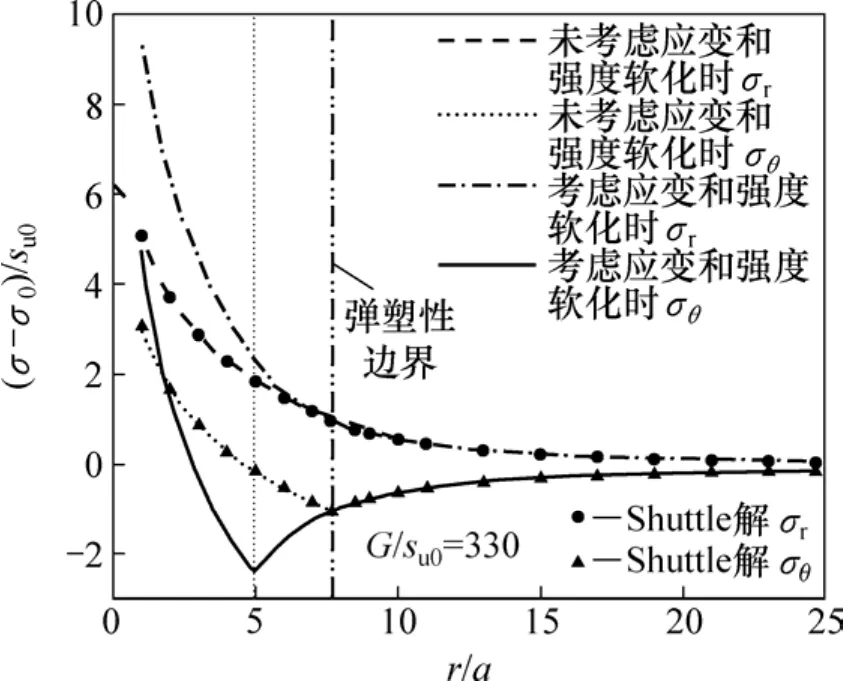
图3 归一化的径向应力和切向应力沿着径向分布Fig. 3 Normalized radial and circumference stress along radial distance
3 参数分析
3.1 刚度系数G/su0对扩孔弹塑性解的影响
图4所示为归一化的圆柱孔壁压力随着刚度系数的变化,其中,μ=0.15,δrem=0.2,ξ95=10。从图 4可以看出:随着扩孔半径增加,孔壁压力先快速增加,然后缓慢变化,最后当扩孔半径超过初始半径的3倍时,孔壁应力保持不变;同时,随着刚度系数G/su0的增加,孔壁应力将会变大,且变化幅度呈现减小趋势。由于刚度系数反映土体抵抗剪切变形能力,说明土体抗剪强度将会对考虑应变率和强度软化的扩孔孔壁应力造成影响。
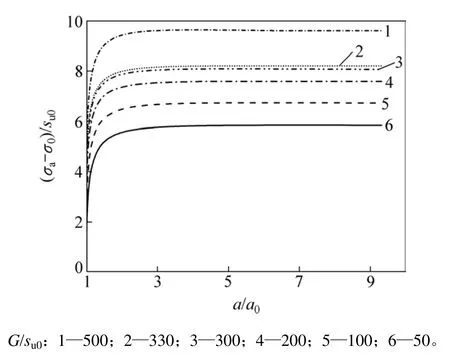
图4 归一化的孔壁压力随着G/su0的变化Fig. 4 Variation of normalized cylindrical cavity pressure with G/su0
3.2 应变率系数μ对扩孔弹塑性解的影响
归一化的孔壁压力、径向应力和切向应力分布随μ的变化分别如图 5和图 6所示,其中,δrem=0.2,ξ95=50,G/su0=330。从图 5可得:随着应变率系数μ的增加,孔壁压力也相应增大,孔壁压力的增长幅度与应变率系数μ的增长幅度基本一致,同时,当应变率系数μ=0.3时,当扩孔半径超过2.5倍初始半径时,其位于衰减区的孔壁应力呈现下降趋势,即孔壁处应力呈现应力软化现象。另外,从图5还可以得出:应变率系数μ越大,孔壁处强度软化现象越明显,且只有当扩孔半径需要超过2.5倍初始半径时,才能够在塑性区呈现出这种现象。

图5 归一化的孔壁压力随着μ的变化Fig. 5 Variation of normalized cylindrical cavity pressure with μ
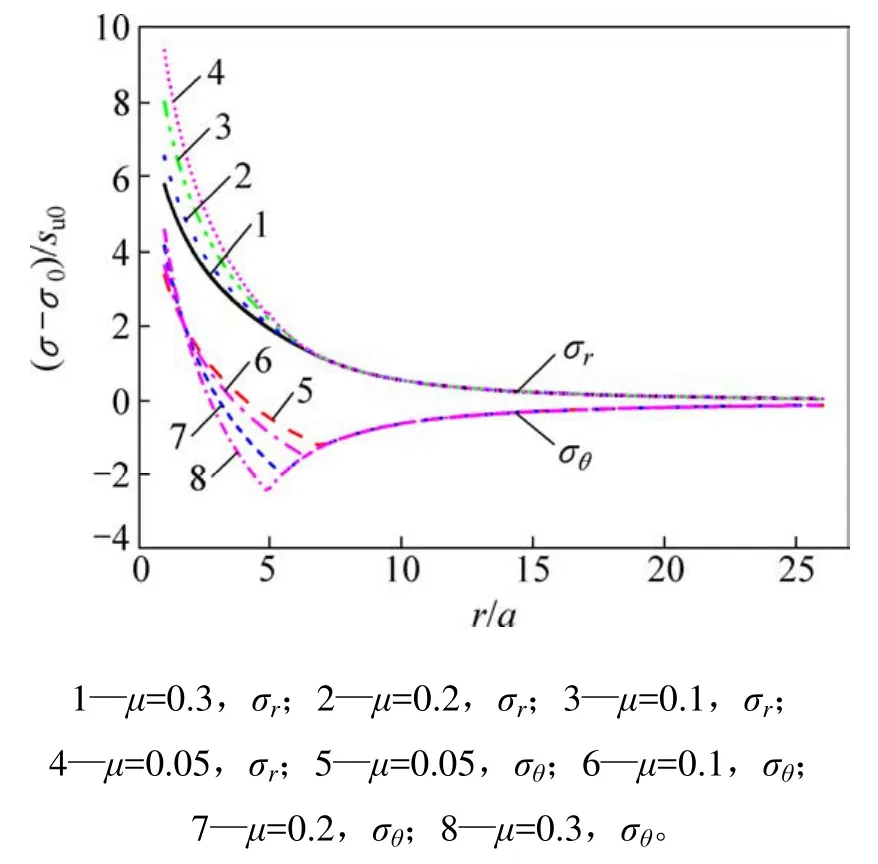
图6 归一化的径向、切向应力分布随μ的变化Fig. 6 Variation of normalized radial and circumference stress with μ along radial distance
从图6可以得出:应变率系数μ越大,其径向应力和切向应力的弹塑性边界越靠近孔壁,即塑性区范围将会越小。同时,分析塑性区应力可得:由于应变率系数μ将会提高孔壁峰值应力,且μ越大,孔壁塑性区相同位置处,其径向应力和切向应力越大。分析塑性区应力变化率可得:μ越大,塑性区应力降低越快,即塑性区强度软化越显现,而位于弹性区的径向应力和切向应力并不会受到应变率系数μ的影响。
3.3 强度软化系数ξ95和δrem对扩孔弹塑性解的影响
图7和图8所示分别为归一化的径向应力和切向应力对强度软化系数ξ95和δrem的影响,其中,μ=0.2,G/su0=330。从图7可知:离孔壁越远处,径向应力越小,而切向应力先减小,后增大,再减小,同时切向应力在塑性区方向会发生改变。而随着ξ95增大,在相同位置处,其应力也会变大。从图7还可以看出:当ξ95超过1时,强度软化系数ξ95对于应力沿着径向分布的影响很小。ξ95越大,塑性区越小,但减小的弧度较小。由于ξ95越小,则累计塑性剪应力越小,也就是发生剪切变形越小,土体呈现压缩变形,即造成在孔壁附近的切向应力较小,而径向应力较大。此外,由于强度软化系数越大,塑性区土体强度软化越快,从而造成应力下降速度越快,而土体屈服强度在不变的情况下,因此,会造成塑性区半径越小,从而越靠近孔壁。
从图8可以看出:强度软化系数越大δrem越大,其孔壁应力越大,同时塑性区范围越小,应力减小得越快,强度软化现象表现得更加明显,同时δrem增长得越快,其对于应力分布的影响越小。由于δrem与土体灵敏度呈现倒数关系,从而可以推断在柱孔扩张过程中,土体灵敏度将会影响土体中应力沿着径向分布。
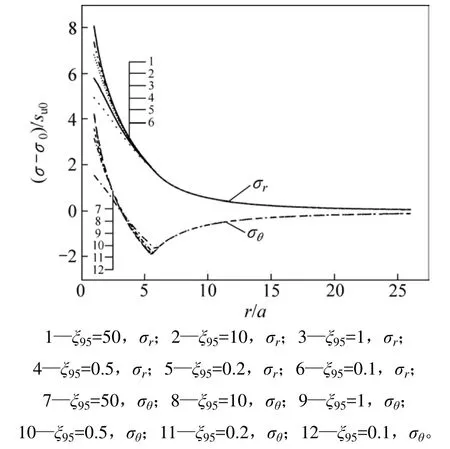
图7 归一化的径向应力和切向应力分布随ξ95的变化Fig. 7 Variation of normalized radial and circumference stress with ξ95 along radial distance

图8 归一化的径向应力和切向应力分布随δrem的变化Fig. 8 Variation of normalized radial and circumference stress with δrem along radial distance
4 结论
1)刚度系数G/su0越大,孔壁应力越大,应变率效应越明显。
2)应变率系数μ越大,扩孔后,孔壁应力越大,塑性区范围越小。应变率系数μ越大,强度软化现象越明显,同时,只有当扩孔半径超过初始半径2.5倍时,孔壁应力才会表现强度软化现象。
3)强度软化系数ξ95越大、塑性累积应变越大,强度衰减得越快,而强度软化系数δrem越大,土体灵敏度越小,强度软化现象越明显。
[1]VESIC A S. Expansion of cavities in infinite soil mass[J].Journal of Soil Mechanics and Foundations Division, 1972,98(3): 265−290.
[2]YU H S. Cavity expansion methods in geomechanics[M]. A H Dordrecht: Kluwer Academic, 2000: 16−18.
[3]BUTTERFIED R, BANERJEE P K. Advance geotechnical analyses[M]. London: Elsevier Applied Science, 1991.
[4]蒋明镜, 沈珠江. 考虑材料应变软化的柱形孔扩张问题[J].岩土工程学报, 1995, 17(4): 10−19.JIANG Mingjing, SHEN Zhujiang. Expansion of cylindrical cavity of materials with strain-softening behavior[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(4): 10−19.
[5]贾尚华, 赵春风, 赵程. 砂土中柱孔扩张问题的扩孔压力与扩孔半径分析[J]. 岩石力学与工程学报, 2015, 34(1): 182−188.JIA Shanghua, ZHAO Chunfeng, ZHAO Cheng. Analysis of expanded radius and internal expanding pressure of cylindrical hole[J]. Rock and Soil Mechanics, 2015, 34(1): 182−188.
[6]肖昭然, 张昭, 杜明芳. 饱和土体小孔扩张问题的弹塑性解析解[J]. 岩土力学, 2004, 25(9): 1373−1378.XIAO Zhaoran, ZHANG Zhao, DU Mingfang. An elastoplastic closed-form approach of approach of cavity expansion in saturated soil based on modified Cam clay model[J]. Rock and Soil Mechanics, 2004, 25(9): 1373−1378.
[7]綦春明, 莫斌, 聂春龙, 等. 饱和土体柱形扩孔时大变形不排水统一解析解[J]. 岩石力学与工程学报, 2009, 28(4): 827−833.QI Chunming, MO Bin, NIE Chunlong, et al. Unified analytical solution for cylindrical cavity expansion in saturated soil under large deformation and undrained conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4): 827−833.
[8]邹金峰, 徐望国, 罗强, 等. 饱和土中劈裂灌浆压力研究[J].岩土力学, 2008, 29(7): 1802−1806.ZOU Jinfeng, XU Wangguo, LUO Qiang, et al. Study on grouting pressure of frasture grouting in saturated soil[J]. Rock and Soil Mechanics, 2008, 29(7): 1802−1806.
[9]章定文, 刘松玉, 顾沉颖. 各向异性初始应力状态下圆柱孔扩张理论弹塑性分析[J]. 岩土力学, 2009, 30(6): 1631−1634.ZHANG Dingwen, LIU Songyu, GU Chenying. Elastoplastic analysis of cylindrical cavity expansion with anisotropic initial stress[J]. Rock and Soil Mechanics, 2009, 30(6): 1631−1634.
[10]ZHOU H, LIU H, KONG G, et al. Analytical solution of undrained cylindrical cavity expansion in saturated soil under anisotropic initial stress[J]. Computers and Geotechnics, 2014,55: 232−239.
[11]ZHOU H, KONG G, LIU H, et al. A semi-analytical solution for cylindrical cavity expansion in elastic–perfectly plastic soil under biaxial in situ stress field[J]. Géotechnique, 2016, 66(7):584−595.
[12]罗嗣海, 侯龙清, 胡中雄, 等. 预钻孔孔径对部分挤土桩挤土效应的影响研究[J]. 岩土力学, 2002, 23(2): 222−224.LUO Sihai, HOU Longqin, HU Zhongxiong, et al. Study on the influence of the diameter of pre-driven borehole on soil-displacement effect of partly soil-displaced piles[J]. Rock and Soil Mechanics, 2002, 23(2): 222−224.
[13]EINAV I, RANDOLPH M F. Combining upper bound and strain path methods for evaluation penetration resistance[J].International Journal for Numerical Methods in Engineer, 2005,63(14): 1991−2016.
[14]DAYAL U, ALLEN J H. The effect of penetration rate on the strength of remolded clay and sand samples[J]. Canadian Geotechnical Journal, 1975, 12(3): 336−348.
[15]梁发云, 陈龙珠. 应变软化 Tresca材料中扩孔问题解答及其应用[J]. 岩土力学, 2004, 25(2): 261−265.LIANG Fayun, CHEN Longzhu. Analytical solution to cavity expansion in strain-softening soils with Tesca yield criterion and its applications[J]. Rock and Soil Mechanics, 2004, 25(2):261−265.
[16]ZHOU H, RANDOLPH M F. Computational techniques and shear band development for cylindrical and spherical penetrometers in strain-softening clay[J]. International Journal of Geomechanics, 2007, 7(4): 287−295.
[17]BISCONTIN G, PESTANA J M. Influence of peripheral velocity on vane shear strength of an artificial clay[J]. Geotechnical Testing Journal, 2001, 24(4): 423−429.
[18]CARTER J P, BOOKER J R, YEUNG S K. Cavity expansion in cohesive frictional soils[J]. Géotechnique, 1986, 36(3): 349−358.
[19]SHUTTLE D. Cylindrical cavity expansion and contraction in Tresca soil[J]. Géotechnique, 2007, 57(3): 305−308.
