基于改进遗传算法的射电望远镜主动面布线优化
2018-06-25申正黄剑辉叶骞
申正,黄剑辉,叶骞
(上海交通大学 机械与动力工程学院,上海,200240)
射电望远镜通过精确的主动面形来接收天体的射电波,对主动面形的精度要求非常高。目前,一些大型射电望远镜采用了基于促动器的主动面技术,如美国的GBT 100 m、意大利的NOTO 34 m、上海的65 m射电望远镜等,来实时补偿由于重力、温度和风压等外界因素引起的主动面变形[1−3]。上海的65 m射电望远镜的主动面系统共有1 104台促动器,1 008块面板,每块面板由4台促动器调整,促动器通过总线进行通讯。保证促动器的工作可靠性是主动面能实时调整的前提,因此,合理地布置总线以及每条总线上的促动器数目就显得尤为重要。通过主动面系统布线来提高促动器的可靠性,目前对该问题的研究较少。许多学者利用智能算法解决生活中的布线问题,如 ANAND等[4−5]利用模拟退火、蚁群算法等算法在大规模集成电路设计中提高芯片电路的集成化,简化加工工艺。在天然气管道布置中,利用遗传算法、蚁群算法等智能算法来解决各种管网形状的布线问题[6−8],提高管路的可靠性。本文作者针对上海65 m射电望远镜,采用改进的遗传算法对其主动面系统的布线问题进行优化。
1 数学模型
1.1 布线问题的实质
根据射电望远镜结构的对称性,取其中的1个15°分区作为研究目标,其他分区的布线方式与此相同。将整个射电望远镜主动面板划分成24个区,每个区共46个节点。射电望远镜在1个15°分区的促动器节点分布平面图如图1所示。
为了简化布线,在不影响布线结果的前提下,将曲面布线问题转化成平面布线问题,转化后的促动器分布如图2所示。根据射电望远镜在实际中的使用情况和优化目标,对布线有如下要求:
1)每条总线从控制箱出发,最后再回到控制箱;
2)每条总线上的促动器尽可能少;
3)所有总线的总长度尽可能小;
4)每条总线沿着辐射梁布置,不同总线只在辐射梁上相交,在图2中,只能沿竖直或水平方向布置。
布线优化是一种多组寻优的最佳路径规划问题,属于一类多旅行商问题(MTSP)[9]。对于MTSP问题的求解,目前常用的算法有粒子群算法、蚁群算法、人工蜂群算法、遗传算法等[10−13]。对于多目标的MTSP问题,朱云飞等[14]给出一种多目标混合遗传算法,RONI等[15]也给出一种多目标遗传算法,并测试了算法的可靠性,对布线优化有较大指导意义。

图1 15°分区促动器实际分布Fig. 1 Actual distribution of actuators in a 15° partition

图2 15°分区促动器节点坐标Fig. 2 Nodes coordinates of actuators in a 15° partition
1.2 MTSP的转化
将MTSP可以转化成TSP,这样就可方便地定义性能指标[9]。转化的方法是:将多余的M−1个旅行商(共M个旅行商)看成是虚拟节点,并依附在其他节点上,TSP路线到达这些虚拟节点时自动转向原点,则对应TSP的解即是原MTSP的解。此时,布线总长需额外考虑虚拟节点到原点的长度,属于非线性问题,如图3所示。

图3 6点MTSP问题转化成6点TSP非线性问题Fig. 3 MTSP-6 to TSP-6 nonlinear transformation
1.3 布线问题的数学模型
从布线角度来看,线路的可靠性主要取决于节点数量,单根总线节点数越多则可靠性越低;线路压降主要取决于线路长度,总线越长则损失的电压越大。因此,整个主动面系统布线问题的优化目标是:满足可靠性要求下使得线路压降最小。相应的MTSP遗传算法的目标函数是:考虑分组数,在节点数存在最大限制的条件下,寻求使得总长度最小的路线,用数学模型表示:
式中:k为布线分组数,与K有关;K是与可靠性有关的最大节点限制数;li为第i个虚拟节点到原点的距离;为第Pi−1个虚拟节点到Pi个虚拟节点之间的路径S的长度;Ni为被虚拟节点分割后的各段节点数量;N为总节点数。
在计算总线长度时,由于要求总线沿辐射梁布置,无跨接,所以,在设计算法时,总线长度不再是一般意义上的欧氏距离,而应该是相应坐标差的绝对值之和。假设A点和B点坐标分别为A(x1,y1)和B(x2,y2),则AB两点之间的线长L为
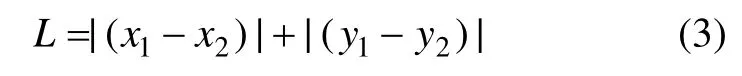
为简便起见,可以将上述带约束的最优化问题转化为无约束问题。引入布线可靠性权重因子a和线路总压降权重因子b,则布线性能指标可以认为是线路总长度和单根总线最大节点数的线性组合。对这2个指标归一化处理。线路总长度归一化系数选择为最大辐射线长,即按辐射状分成45组,每组只包含起点和1个节点;最大节点数归一化系数选择为除去起点的线路节点数,此处为 45。归一化之后的优化目标函数为

式中:′为考虑每条总线只有1个节点时,第i条总线的长度;N为总节点数。
综上,通过改变a和b,算法在迭代过程中将同时对线路总长度、最大节点数、分组数这3个参数进行全局优化,最终得到布线最优的方案。
2 遗传算法设计
2.1 个体编解码方式
本文采用十进制的编码方式,现假设共有7个城市(1为起点,不参与排序),其中一条染色体编码如下(斜体阴影数字表示虚拟节点,下同):
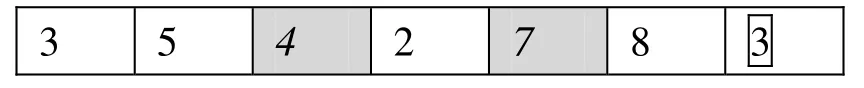
此时,染色体共有7位,前面6位是去除起点后的任意排序,代表路径。最后一位(带字符边框的表示分组数,下同)代表布线分组数为3,即对应2个虚拟节点4和7。则3组线路分别是:

为了方便地处理变组数的情况,可以将染色体拆分成2个部分。
1)路径向量,长度为1×(N−1)的向量。

2)虚拟节点向量,长度为 1×(N−1)的向量,前(N−2)位代表虚拟节点,不足补0,第N位是分组数标志,取值范围[1,(N−1)]。

在设计算法时将路径向量和虚拟节点向量存储在一个矩阵里。存储形式如下:

2.2 适应度函数
根据布线优化的数学模型可知,适应度是总线长度和最大节点数的函数,定义为

式(5)中的所有变量均可由路径向量和虚拟节点计算得出。
2.3 遗传操作算子
在传统遗传算法中,上一代通过选择、交叉、变异等操作得到下一代。由于适应性差的个体也参与交叉变异,所以,算法的收敛速度会较慢。若先将种群分成若干个小组,在小组内进行遗传变异,每次迭代后即重新随机分组,则在避免算法早熟的同时可以提高收敛速度。因此,本文先对种群进行均匀分组,组内个体进行适应度计算,只保留最好个体,之后该个体通过不同方向的变异产生新个体,每次迭代后再进行新的随机分组以避免早熟。对本文所研究的布线优化问题,个体的差异由以下3个方面决定:MTSP转化成 TSP后的路径向量、虚拟节点的数量(布线分组数)、虚拟节点的位置。现假设有8个城市,种群随机分组,每组有12个个体,其染色体编码均是随机产生,经过适应度计算后,选出组内最好个体(如表1所示)。然后将该个体复制11个,并控制这11个个体按照以下方向进行变异。
2.3.1 对路径向量变异
算法随机产生2个断点(加粗斜体数字),假设为第2位和第6位。对复制个体1~3号进行路径变异操作。

表1 最好个体Table 1 The best individual

1)交换操作。
交换第2位和第6位上的基因,得到1号子代个体的路径向量如下:

2)反转操作。
将第2位和第6位中间的基因段反转排列,得到2号子代个体的路径向量如下:

3)移位操作。
将第2位和第6位中间的基因段进行循环移位操作,即整个基因片段环形右移1位,基因片段最后一位变成第1位,变异后的3号子代个体的路径向量如下:

2.3.2 对虚拟节点向量变异
4号子代个体生成方式为:路径向量不变(仍为最好个体路径向量),分组数不变,在原序列的基础上随机产生新的虚拟节点,产生新的虚拟节点向量如下:

5号子代个体生成方式为:路径向量不变,分组数随机产生,且根据分组数重新随机配置虚拟节点位置,产生新的虚拟节点向量如下:
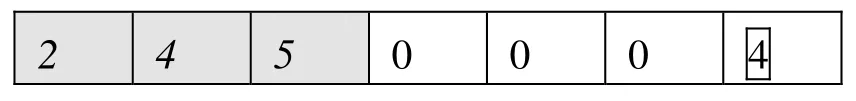
2.3.3 组合变异
子代个体6~8号由最好个体的变异路径向量和子代个体4号的虚拟节点向量组合产生;子代9~11号由最好个体的变异路径向量和子代个体5号的虚拟节点向量组合产生。
算法中每个分组都进行相同的遗传变异操作,最终产生新一代种群。在下一次迭代时种群将会重新随机分组,以保证种群的多样性。整个遗传变异过程如流程图4所示。
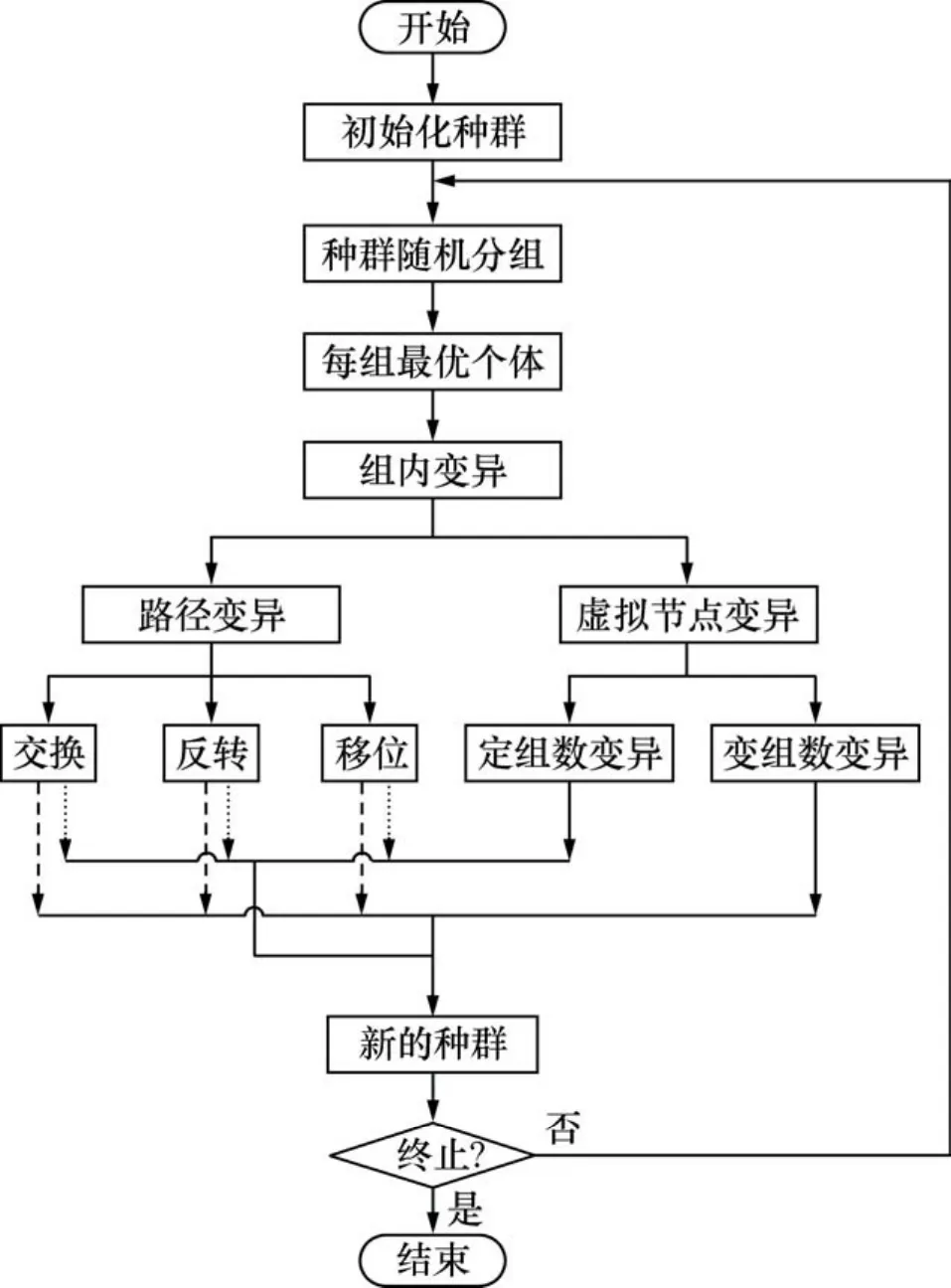
图4 遗传算法计算流程图Fig. 4 Flow chart of genetic algorithm
3 优化结果及讨论
假定总线长和可靠性同等重要,考虑到较N大很多(约 10倍),所以,设定可靠性权重因子a=10和线路总压降权重因子b=1。然后,利用遗传算法进行优化,得到优化结果(见图5),相应的适应度收敛曲线如图6所示。在实际应用时,可以根据总线长和可靠性的不同要求调整权重因子,得到相应的优化结果。
为了测试算法的稳定性,在相同的条件下多次运行,得到的优化结果如表2所示。采用传统遗传算法对同样的问题进行求解,优化结果如表3所示。测试中用到的主要参数如表4所示。
从表2和表3可以看出,考虑总线长和可靠性同等重要时,最优方案是最短线长为64的2组布线(排布方式不唯一)。在10次测试中,总线长有8次都收敛于64,说明算法稳定性很高。与传统遗传算法相比,该程序的平均运行时间为 2 min,而传统遗传算法平均运行时间大于5 h,计算效率有明显提高;此外,传统遗传算法很不稳定,容易出现丢点的现象,最优的总线长为71。

图5 布线优化分组结果Fig. 5 Optimized grouping results of wiring

图6 适应度变化曲线Fig. 6 Changing curve of fitness

表2 分组遗传算法测试结果Table 2 Test results of group-based GA

表3 传统遗传算法测试结果Table 3 Test results of general GA

表4 2种算法主要参数Table 4 Main parameters of two algorithms
传统遗传算法出现运行时间长、不稳定的情况是由于适应性差的个体在算法中参与了交叉变异,减慢了算法向最优解收敛的速度,同时容易使算法早熟。从结果可以看出:减少适应性差的个体的参与度,并提高变异概率会提高算法的性能。
通过对比可以看出:在稳定性、计算效率和优化结果方面,本文基于分组优化的遗传算法比传统遗传算法有很大的提升,证明了该算法的正确性和有效性。
4 结论
1)提出了一种改进的遗传算法,该算法利用分组优化的思想和针对组内最好个体的变异方式,有效地提高了遗传算法的收敛速度和算法稳定性。
2)改进的遗传算法可以对射电望远镜主动面系统的布线问题进行优化,得到最小压降和最大可靠性的布线方案,使主动面系统能更好地实时补偿射电望远镜的表面变形,进而提高射电望远镜的观测性能。
[1]PRESTAGE R M, CONSTANTILEES K T, HUNTER T R, et al.The green bank telescope[J]. Proceedings of the IEEE, 2009,97(8): 1382−1390.
[2]赵卫, 叶骞, 冯正进. 射电望远镜主动反射面控制技术简析[J]. 现代雷达, 2011, 33(5): 85−90.ZHAO Wei, YE Qian, FENG Zhengjin. Analysis of control technology for active reflector of radio telescope[J]. Modern Radar, 2011, 33(5): 85−90.
[3]杜彪, 伍洋, 张一凡, 等. 大口径反射面天线技术综述[J]. 无线电通信技术, 2016(1): 1−8.DU Biao, WU Yang, ZHANG Yifan, et al. Survey of large aperture reflector antenna technology[J]. Radio Communications Technology, 2016(1): 1−8.
[4]ANAND S, SARAVANASANKAR S, SUBBARAJ P. A multiobjective optimization tool for very large scale integrated nonslicing floorplanning[J]. International Journal of Circuit Theory & Applications, 2013, 41(9): 904−923.
[5]CHEN Guotong, GUO Wenzhong, CHEN Yuzhong. A PSO-based intelligent decision algorithm for VLSI floorplanning[J]. Soft Computing, 2010, 14(12): 1329−1337.
[6]蒋永明. 基于蚁群算法的天然气长输管线优化设计研究[D].哈尔滨: 哈尔滨工业大学市政环境工程学院, 2007: 31−38.JIANG Yongming. The research about optimization design of natural gas pipeline based on ant colony algorithms[D]. Harbin:Harbin Institute of Technology. School of Municipal and Environmental Engineering, 2007: 31−38.
[7]吕木英. 基于遗传算法的城市燃气管网最优化布局研究[D].武汉: 武汉理工大学能源与动力工程学院, 2009: 28−36.LÜ Muying. Study on optimization of urban gas distribution network based on genetic algorithm[D]. Wuhan: Wuhan University of Technology. School of Energy and Power Engineering, 2009: 28−36.
[8]刘奇. 天然气管道调度优化研究[D]. 南充: 西南石油大学石油与天然气工程学院, 2014: 35−39.LIU Qi. Study on the optimization of natural gas pipeline scheduling[D]. Nanchong: Southwest Petroleum University.College of Petroleum Engineering, 2014: 35−39.
[9]俞庆生, 林冬梅, 王东. 多旅行商问题研究综述[J]. 价值工程,2012, 31(2): 166−168.YU Qingsheng, LIN Dongmei, WANG Dong. An overview of multiple traveling salesman problem[J]. Value Engineering,2012, 31(2): 166−168.
[10]CARTER A E, RAGSDALE C T. A new approach to solving the multiple traveling salesperson problem using genetic algorithms[J]. European Journal of Operational Research, 2006,175(1): 246−257.
[11]PAN Junjie, WANG Dingwei. An ant colony optimization algorithm for multiple travelling salesman problem[C]//International Conference on Innovative Computing, Information and Control. Los Alamitos: IEEE Computer Society, 2006:01446.
[12]ZHANG Z, CHEN Y, CHENG H, et al. MTSP based solution for minimum mobile node number problem in sweep converge of wireless sensor network[C]//International Conference on Computer Science and Network Technology. Piscataway: IEEE,2011: 1827−1830.
[13]VENKATESH P, SINGH A, VENKATESH P, et al. Two metaheuristic approaches for the multiple traveling salesperson problem[J]. Applied Soft Computing, 2015, 26: 74−89.
[14]朱云飞, 蔡自兴, 袁琦钊, 等. 求解多目标旅行商问题的混合
遗传算法[J]. 计算机工程与应用, 2011, 47(7): 52−56.
ZHU Yunfei, CAI Zixing, YUAN Qizhao, et al. Hybrld genetic algorithm for multiple-objective TSP[J]. Computer Engineering and Applications, 2011, 47(7): 52−56.
[15]RONI M A, RAHMAN S. Using Genetic Algorithms to minimize the distance and balance the routes for the multiple Traveling Salesman Problem[J]. Evolutionary Computation,2015, 41(6): 3171−3178.
