基于预测前馈PI控制的单相PWM整流器的研究

胡治国，王 飞，李向前

（1.河南理工大学 电气工程与自动化学院，焦作 454000；2.广东珠海格力电器股份有限公司，珠海 519000）

0 引言

近年来，PWM整流器在工业和民用方面的用途愈加广泛，随之而来的如何减少各种能量损耗的研究越来越多。单相电压型PWM整流器由于其诸多优点，如谐波含量少、运行功率接近单位功率因数、可以在电网与用户之间实现双向能量流动等[1,14]。其中，单相电压型PWM整流器在可再生能源的研究中有着举足轻重的地位，其相应控制方式的研究也随之成为热门。

在单相电压型PWM整流器系统控制策略研究中，直流侧负载的改变和电网侧电压纹波会对直流侧输出电压的稳定性和快速动态响应产生较大的影响，而直流侧直流母线电压稳态特性和快速响应能力是衡量单相PWM整流器系统控制方法优劣及输出波形质量好坏的两个重要方面[6]。所以提高整流器控制系统抗扰动能力和提升动态响应速度有着非常重要的意义[8,14,15]。

根据网侧电流控制方式不同来分，单相PWM整流器主要采用电流开环和闭环两种控制方式。电流开环控制优点是结构简单，缺点是抗扰动性较差且动态响应慢。电流闭环控制是通过采用电流前馈策略有效地解决了上述问题，使得系统的稳定性和响应速度等性能指标得到改善[5]。

双闭环控制在目前整流器的相关研究中最为广泛，但是常见的双闭环控制无法实现对电网侧电流的无静差控制，使PI调节器无法得到充分的利用[2]。谐振控制器，由于减少的相位裕度会导致潜在的性能下降，虽然在文献[3]中提出对结构行改良，即在其谐振控制器上添加比例环节能有效的防止这种情况。但是改进的比例谐振控制器改善了低频调节性能，且新引入的平行路径将增加低频和高频响应之间的耦合。文献[2,8]设计了一种基于预测电流前馈控制算法，以达到实现网侧电压控制器实时调控的目的，使得系统在不同的电网电压下都能稳定工作。这种控制策略的缺点是，响应速度较慢，纹波较大，稳定性较差。

针对以上缺陷，采用基于d-q坐标变换[1,5,11,12]的前馈解耦控制策略以达到实现整流器系统单位功率下运行且输出的直流电压稳定。考虑到电网谐波和输出侧直流负载的对输出电压的影响[7]，设计了一种预测前馈PI联合控制方式，以提高系统的动态性能。

1 单相电压型PWM整流器的基本原理及数学模型

单相电压型PWM整流器的拓扑结构如图1所示。

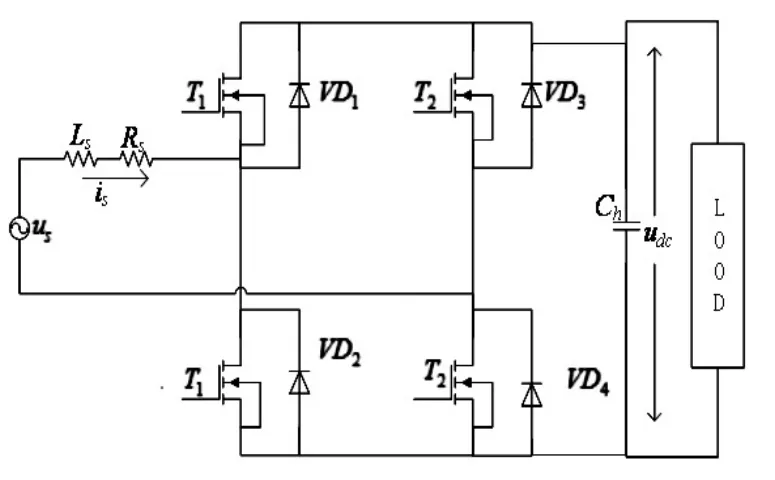
图1 单相电压型PWM整流器拓扑结构

由图1知，该单相电压型PWM整流器主要三部分构成：交流回路、功率开关管桥电路和直流回路。us、is、Ls分别为网侧电压、电流、电感；交流侧等效电阻一般比较小，udc为直流负载两端的电压，T1～T4为全控型功率场效应管；VD1～VD4为续流二极管与功率开关管相并联，作用为功率开关管断开时，对整流过程中产生的无功分量进行缓冲处理；电容Ch为直流滤波电容，主要作用是为高次谐波分量提供低通阻抗通路同时降低直流母线电压纹波。从整个拓扑结构上看，单相电压型PWM整流器具有能量双向流动、消除谐波分量、均衡网侧电压和直流侧电压的作用。

单相电压型PWM整流器采取一定的控制方式是，对T1～T4的开通与关断进行控制，得到一个与电网电压us同频率的一个正弦电流波形。理想状态下电网电压us恒定，网侧电流is的幅值和相位取决于正弦调制波的幅值以及与网侧us之间的相位差。因此只需要对正弦调制波中基波的幅值和相位进行控制，就可以控制is与us之间的关系从而使得控制系统达到具备能量双向流动和单位功率因数的运行目的，使得该单相电压PWM整流器电路在整流与逆变两种状态工作。

单相电压型PWM整流器电网侧KVL回路方程和直流侧KCL回路方程为：

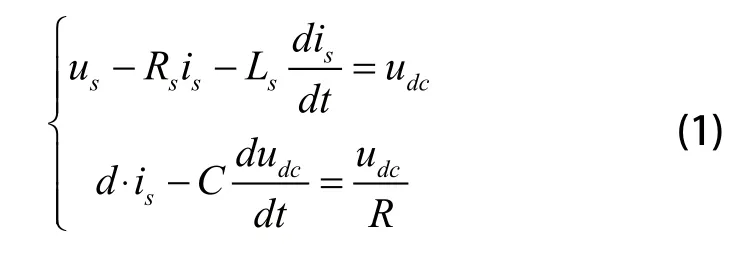
d为控制脉冲占空比，电网侧的电压和电流设为：

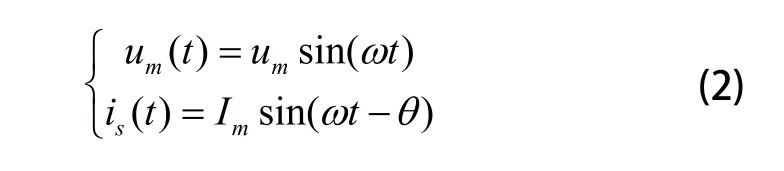
任意单相正弦向量x(t)均可分解为：

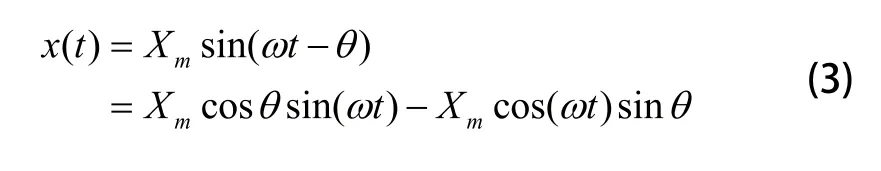
令：

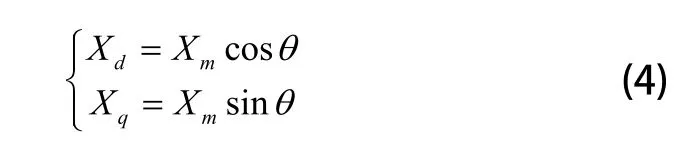
Xd和Xq是d-q旋转坐标系中的直流量。三相PWM整流器可以直接进行Clark变换以及Park变换，即三相静止abc坐标系的电压变量通过变换计算转化成两相同步d-q旋转坐标系中的电压分量。单相PWM整流器不能直接进行Clark变换，因此需要构造一个与网侧电流交流量相正交的交流量以达到Clark变换的效果，从而可以经过Park变换得到虚拟的两相静止坐标系，然后可以用旋转坐标变化将交流侧电流is转化为：

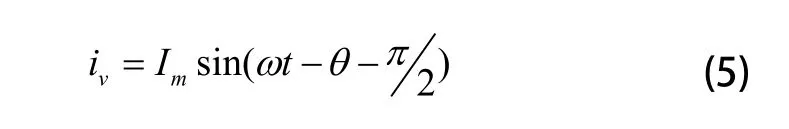
从而得出：

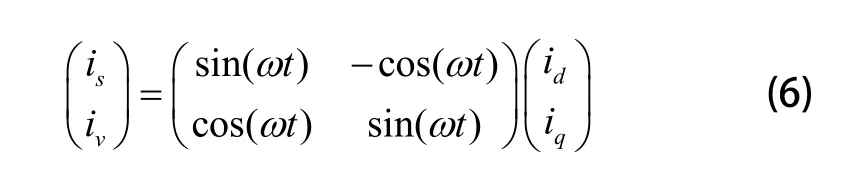
则：

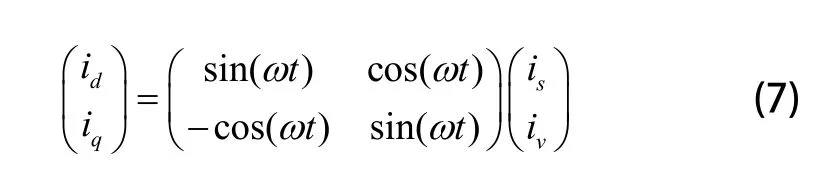
由式(3)和式(4)可得：

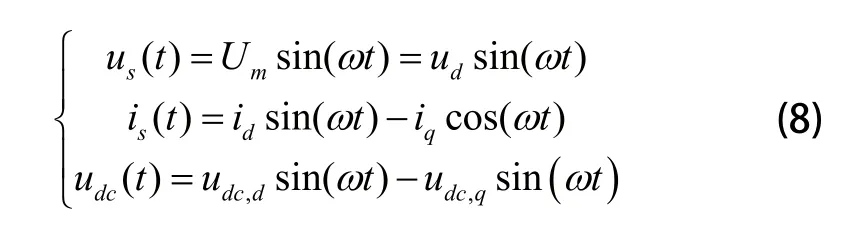
将式(8)代入式(1)可以得到：

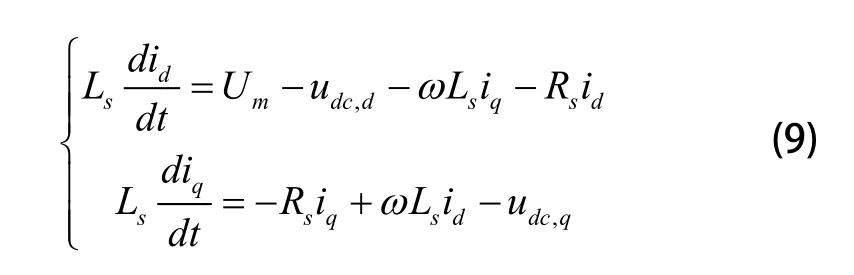
2 单相PWM整流器控制策略

单相电压型PWM整流器控制指标是：1）直流母线电压稳定；2）单位功率因数下运行。要达到这两个目标需要对电网侧电流和直流侧电压进行控制且要考虑到电网侧谐波分量和输出侧负载突变对输出电压的影响[4]。

从式(9)中可以看到，在控制过程中两个变量id和iq相互影响，存在耦合，不能独立控制。将三相电压型PWM整流器中经常采用前馈解耦控制策略[9]，引用到单相PWM整流器的控制中，其控制方程为：

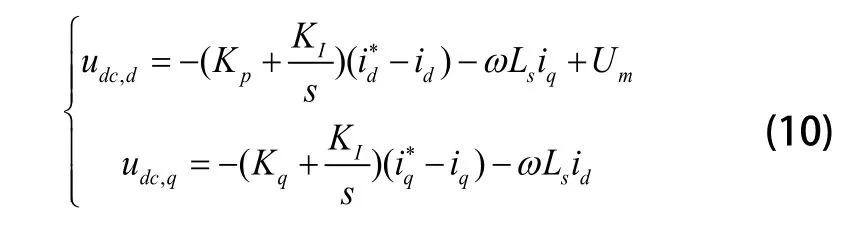
式(10)代入式(9)中得：

可以看出式(11)中id、iq完全解耦，能够实现独立控制彼此不受的影响，i*d为有功电流给定值，由电压外环控制系统经过PI控制器所得；i*q为电流无功分量给定值，令其为零则可以达到整流器系统的单位功率因数运行目的。其系统控制框图如图2所示。

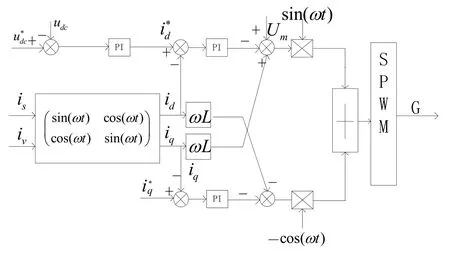
图2 基于旋转坐标系的前馈解耦控制框图

3 预测前馈控制策略

为了提升系统的抗干扰能力，动态响应速度和动态性能，本文设计了预测前馈PI联合控制策略，可以让系统具有快速响应和较高的稳态性能。预测前馈PI联合控制策略原理图如图3所示，在每个采样周期，对输出的电流Idc，k-1和电压vdc，k-1进行采样，采样结果经过延迟模块延迟一个采样周期得到下一个控制周期输出的电压值vdc，k，然后将电流Idc，k-1与电压差的乘积的差值送入积分控制器，其输出值与电压外环PI控制器的输出值相加，经计算得出电流值的参考值i*d与前馈解耦控制器电流分量id相减输入到下一级控制器。然后将经过一系列运算得到的电压值进行标幺化与三角波相比较得到整流器SPWM的控制信号，使得整流器在下一个控制周期输出的实际电压值与其相同。这样就实现了整流器的负载电压波形能与参考电压一致，在减少电压纹波的同时可以大大提高整流器输出电压的动态响应速度和系统动态性能。

在改进的控制中，是H桥的调制信号，da和db是每个H桥腿的占空比。Id和Iq为电网侧电流有功和无功分量，线性直流母线电压的一阶动态方程为：

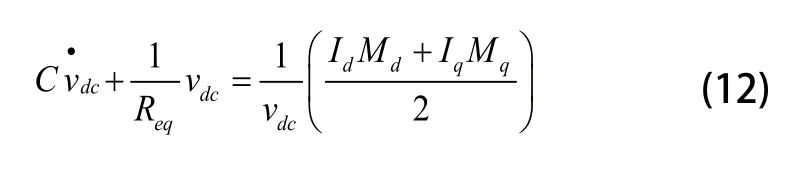
式(12)可以看成是伯努利一阶常微分方程，因此可以通过线性引入并代入式(12)得：

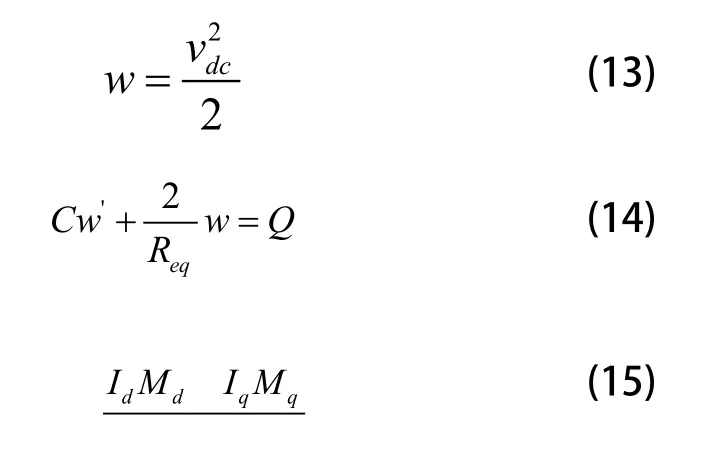
在电容滤波中，假设直流侧电流比直流电压的动态响应快的多，此时Md=U，Mq=0，U即电网侧的电压；电压控制器的输出作为参考电流可得出闭环参考电压w*到w的传递函数：

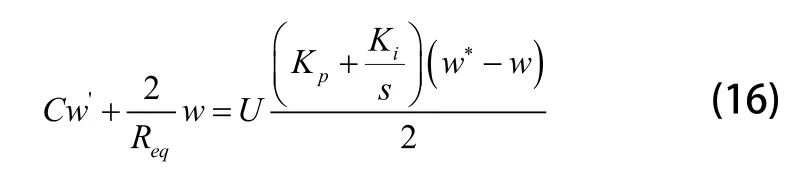
闭环传递函数中w*到w为：

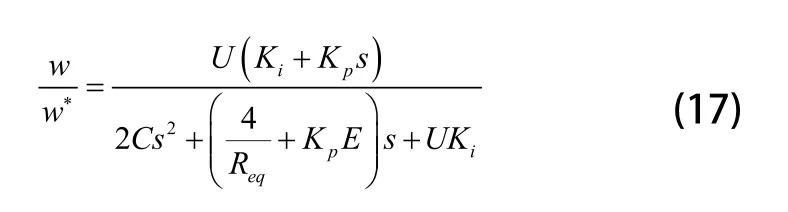
固有频率和阻尼因子的计算公式为：

式(18)和式(19)将用于调整PI控制器的参数为了有快速的动态响应，稳态下直流能量方程为：

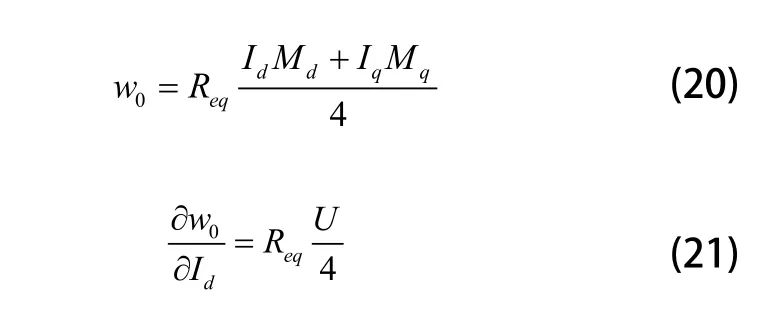
Req移至左侧并由式(13)可得：

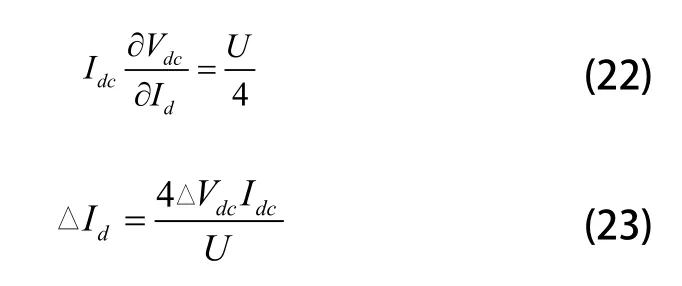
作为前馈项可以有：

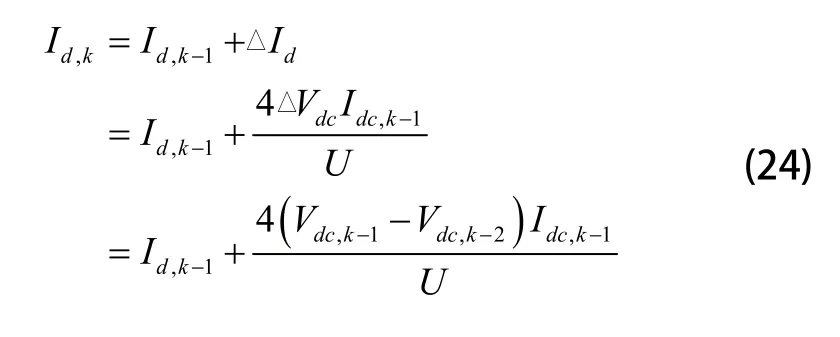
这是一个离散积分函数，其电压差作为输入，增益为基于预测前馈PI联合控制策略下的直流母线电压器结构如图3所示。

图3 直流电压的控制框图

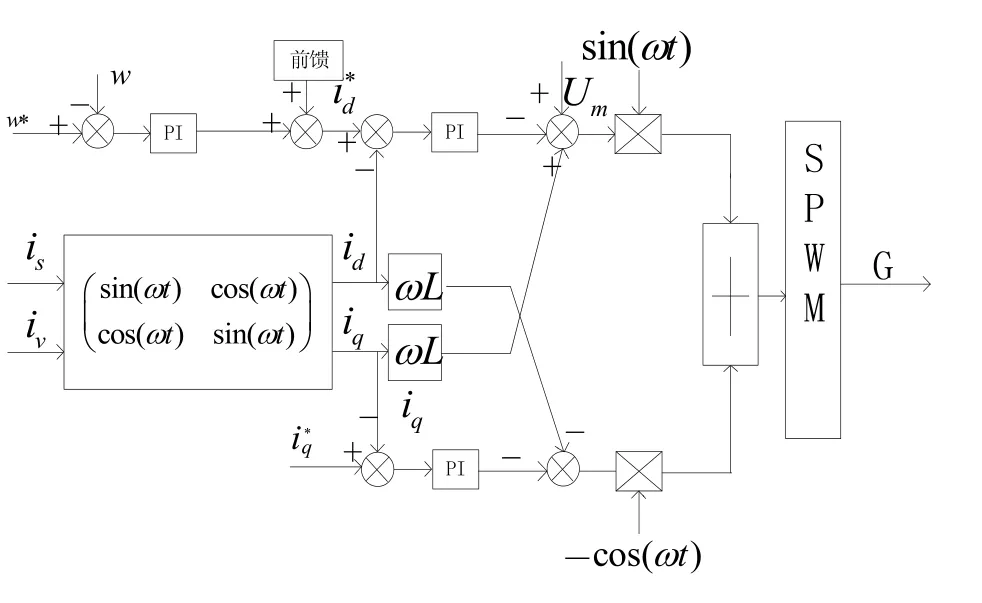
图4 改进后的控制框图

4 仿真研究

使用MATLAB/simulink对本文提出的控制策略进行建模和仿真。在非线性PID的控制器的具体设计中，首先进行PI控制器的整定，可以参照常规整定[16]确定PI控制器的初值，然后结合仿真确定最终值。仿真参数为：网侧电压为us=220V，频f=50Hz，网侧电感为L=0.5mH，网侧等效电阻为Rs=0.026；直流侧电容为C=30mF，直流母线电压u*=400V，负载电阻R=35。开关器件的开关频率为10kHz，负载是电容与电阻并联的线性负载。图5分别给出了传统整流器双闭环控制策略和预测前馈PI联合控制策略在相同的负载下的整流器输出直流电压波形。图7为加入较大负载突变下的直流母线电压变化形。

图5 非线性负载下的仿真波形

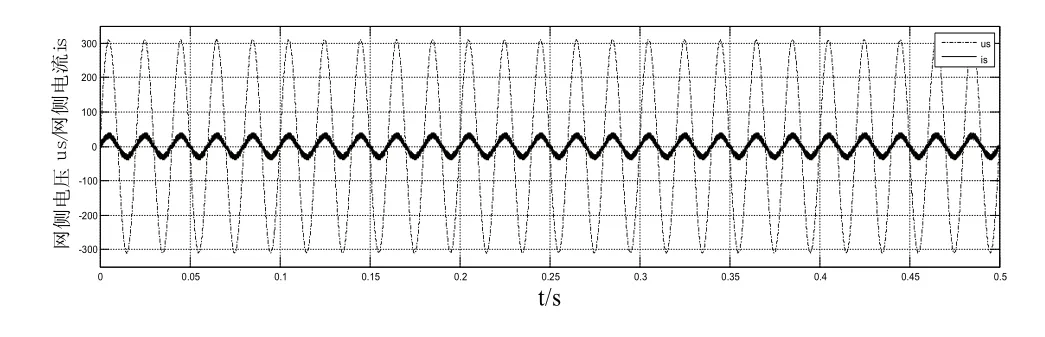
图6 网侧电压和网侧电流波形

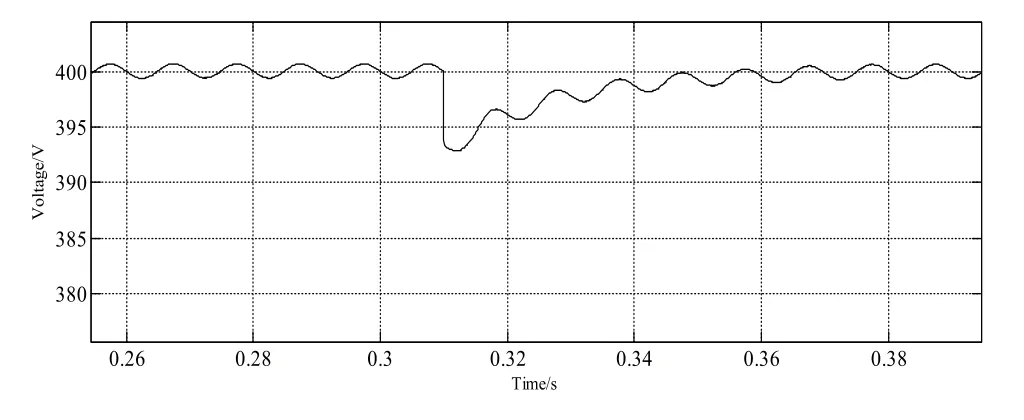
图7 扰动时的直流母线电压波形

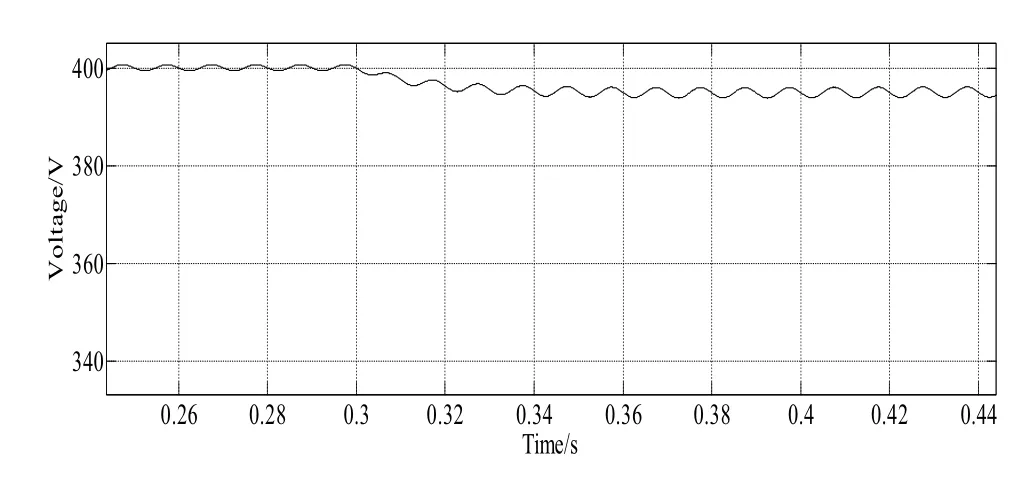
图8 传统控制策略下的直流母线电压扰动波形

由仿真结果对比可知，传统的电压控制策略在非线性负载时，波形存在超调，响应速度较慢等缺点，这样的波形输出在对固态变压器DC-DC级的研究中所不能接受的。采用新的控制策略，由图5可知直流母线电压输出波形在0.05s左右时系统进入稳定状态且在此之前超调几乎为零，直流母线电压稳定在400V，如图6所示，电网侧电压和电网侧电流为正弦波无相位差。在图8中系统在传统的控制策略中无法在加入扰动的情况下，快速回复，也有其他的控制策略但会导致较大的压降并且回复稳定速度较慢，无法应用于实际系统中。与图8相比图7所示是在0.333s时刻引入较大负载突变时直流母线电压的波动情况，仿真时间为0.5s。从图中可以看出加入预测前馈控制时的直流母线电压在负载突变时能迅速的达到稳定状态。说明预测前馈控制方案可以使系统获得较好的输出波形，提高系统的抗扰动性。结果验证了改进的控制方案的有效性。结果证明基于预测前馈PI联合控制策略单相PWM整流器系统具有良好的非线性负载能力能很好地消除谐波，能快速且平稳进入稳定状态，整流器的输出波形较好且功率因数近似为一，符合控制要求，验证了该控制策略的可实施性。

5 结论

在对比传统控制方式的优缺点的基础上提出了一种预测前馈PI联合控制方式。在Matlab/Simulink中搭建了相关的仿真模型，对加入预测前馈控制方式的系统和传统控制方式下的系统进行仿真对比。仿真结果表明，该策略不但可以提高整流器系统的响应速度和降低电压超调量，而且可以提高整流器系统的动态性能并增加其抗干扰能力。同时改进的控制方式采用的是周期预测前馈可以使PWM整流器摆脱对系统参数的敏感依赖性。验证了本文所提出控制方式的正确性以及有效性并为固态变压器的后续研究提供良好的基础，保证后续研究工作的正常进行。

[1]张兴.PWM整流器及其控制策略的研究[D].合肥工业大学,2003.

[2]于蓉蓉,魏学业,吴小进,覃庆努.一种改进型预测电流控制算法[J].电工技术学报,2010,25(7):100-107.

[3]She, Xu et al.Review of Solid-State Transformer Technologies and Their Application in Power Distribution Systems[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2013:186-198.

[4]魏建军,胡治国,艾永乐.APF直流侧电压波动原因及稳定控制研究[J/OL].河南理工大学学报(自然科学版),2015,34(04):532-536,546.

[5]卢健康,邢益巽.PWM整流器直接功率控制策略仿真研究[J].计算机仿真,2012,29(8):291-295.

[6]叶满园,曹晖,袁义生.改进型电压预测控制逆变器的研究[J].电力电子技术,2009,43(7):60-62.

[7]孙毅超,赵剑锋,季振东,姚晓君.一种基于虚拟电路闭环的单相PWM整流器控制新方法[J].电工技术学报,2013,28(12):222-229.

[8]肖汉,曾岳南,唐雄民.基于旋转坐标变换的单相电压型PWM整流器系统仿真[J].通信电源技术,2009,26(5):43-46.

[9]宋芸,冯乃光.单相全桥PWM整流器输入电流内环式控制方法的分析与仿真比较[J].现代电子技术,2013,32(4):29-33.

[10]余发山,刘根峰,张宏伟,耿冲.单相PWM整流器前馈解耦控制策略研究[J].电源技术,2016,40(10):2068-2070.

[11]J Salaet,S Busquet,J Bordonau.A New Strategy for Decoupling Direct and Quadrature Currents in a Rotating Frame Current Regulator[J].IEEE Power Electronics Specialists Conference,2006:1-7.

[12]郎永强,徐殿国,HADIANAMREI S R,马洪飞.三相电压型PWM整流器的一种改进前馈控制策略[J].中国电机与控制学报,2006,10(2):160-163,170.

[13]赵仁德,贺益康,刘其辉.提高PWM整流器抗负载扰动性能研究[J].电工技术学报,2004,19(8):67-72.

[14]Makoto Saito,Nobuyuki Matsui.Modeling and Control Strategy for a Single—phase PWM Rectifier using a Single—phase Instantaneous Active Reactive Power Theory[J].International Telecommunications Energy Conference,2003:573-578.

[15]R S Pena,R J Cardenas,J C Clare，G M Asher.Control strategies for voltage control of a boost type PWM convener[J].PESC,2001:730-735.

[16]杨耕,罗应立.电机与运动控制系统[M].清华大学出版社,2006.