基于排队论的环形穿梭车系统运行参数分析

向 旺，吴 双，张可义，徐 健，王弘扬

（北京机械工业自动化研究所有限公司，北京 100120）

0 引言

近年来自动化立体仓库系统在食品、医药、烟草、玻纤、家具等行业应用日渐广泛，以自动化立体仓库系统为核心的相关物流设备趋于多元化，技术性能和水平也不断提高。RGV（Rail Guided Vehicle）轨道式穿梭车是集各种高新技术于一体，既可作为自动化立体仓库系统的辅助系统，也可作为独立的输送系统，因其输送速度快、自动化程度高、灵活性好而被广泛采用[1]。早期的RGV多采用直轨单车往复式运动模式，很难满足多站台取货送货的整体运送需求，为此直轨双车和环轨多车方式的轨道式RGV应运而生[2]。

环轨多车模式RGV系统，由于采用封闭轨道，单向环轨绕圈行驶，在运行过程中易出现堵塞和空跑的情况，降低运行效率。其系统的轨道长度（直道长度和弯道长度）、平均行驶速度（直道平均速度和弯道平均速度）、RGV小车数量等参数与系统出入库效率息息相关，在系统的规划中这些运行参数亦难以确定，因环形RGV系统所起的关键性枢纽作用，所以对环形RGV系统运行参数的分析具有非常重要的实际意义。

本文运用排队论理论对环形RGV系统进行数学模型抽象及分析，并结合B厂自动化立体仓库项目环形RGV系统的实例利用排队论原理对其进行运行参数分析与评估。

1 环形穿梭车系统的排队论模型

1.1 系统概述

B厂自动化立体仓库系统有14台巷道式堆垛机，其环形RGV系统由14个库端入库站台，14个库端出库站台，2个入库口站台，3个出库口站台，7台RGV小车和2个RGV维修工位组成，其平面简图如图1所示。

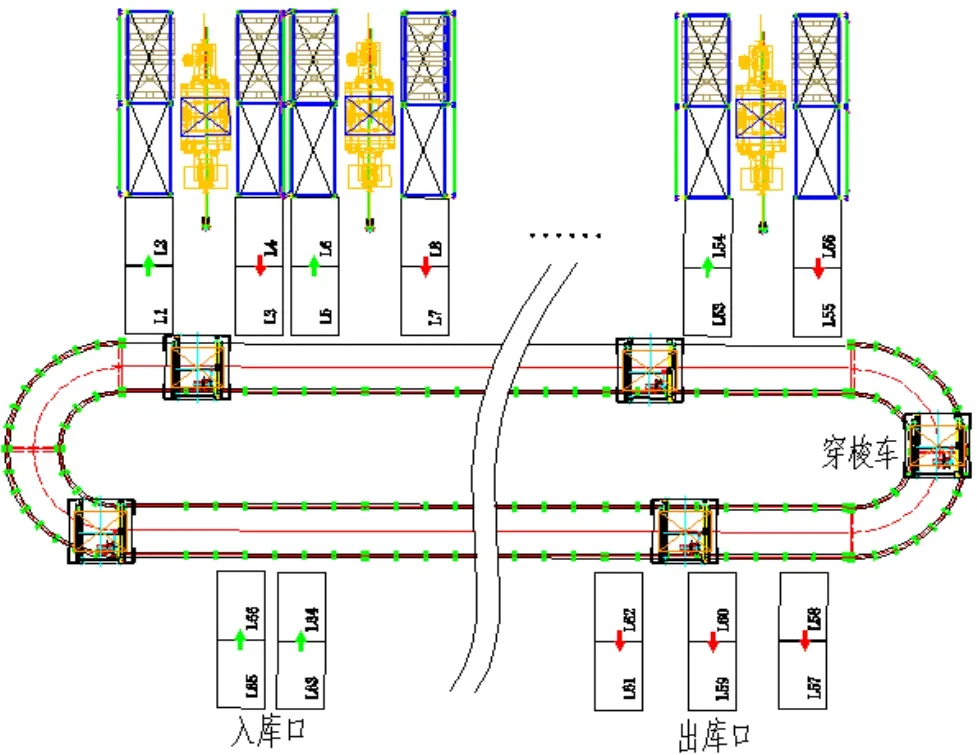
图1 环形穿梭车系统

系统运行工作流程简述：

入库作业：叉车将装好货物的托盘放置于入库口链式输送机上，输送至端头处链式输送机（本文称之为站台），再由穿梭车搬运至库端链式输送机上，由链式输送机输送至库端入库站台，最后由巷道式堆垛机将托盘搬运至上位调度系统下发的货格地址处存放。每个托盘绑定有超高频RFID芯片，在入库口经RFID读码器获取托盘信息，并随托盘的运送传递信息，以供上位管理和监控系统记录和使用。

出库作业：上位管理系统根据订单发货需求，给巷道式堆垛机下发出库作业。堆垛机将出库作业指定货格内装好货物的托盘取出，搬运至各巷道库端出库站台，再由穿梭车搬运至出库口站台以发货。

自动化立体仓库系统满负荷运行时，堆垛机大量出入库作业，RGV小车需做大量搬运任务。图1所示系统中，出入库托盘的搬运任务是随机的，链式输送机长度、环形轨道长度，RGV小车直道和弯道行走速度是确定的，RGV小车和站台接、送托盘的时间也是确定的。托盘输送至站台，小车获取搬运任务，到小车搬运托盘至目的站台，校核目的地址，这其中存在网络延时，该时间与控制系统运算速度和网络传输的延迟有关，这里取0.5s。系统相关参数如表1所示。

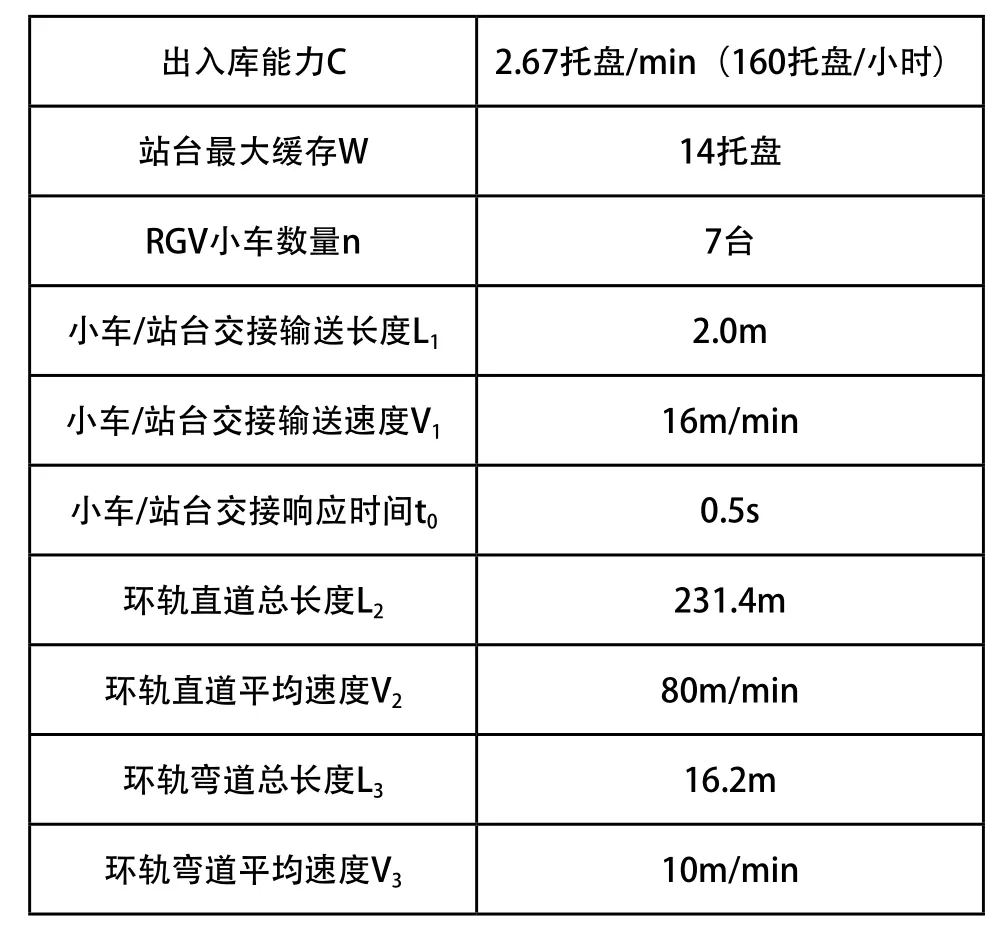
表1 系统相关参数

1.2 排队论基础理论

排队论（Queuing Theory）也称随机服务系统理论，是研究、解决排队问题而发展起来的一门学科。它应用于一切服务系统，包括生产管理系统、交通运输系统、通讯网络系统、存储系统等，排队论的一般模型如图2所示[3]。排队论主要对服务系统排队过程的几个数量指标进行分析、研究，提供参考与决策，进一步探讨最优化问题。

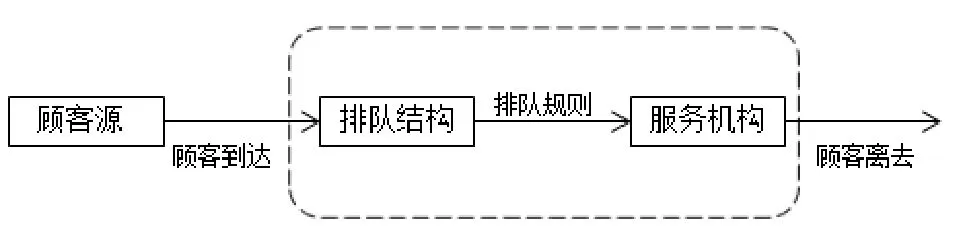
图2 排队模型框图

1.3 系统排队模型的建立

在图2所示的排队模型中，托盘视为顾客，RGV小车视为服务机构，将所有出入库站台视为一合并的站台列，托盘到达站台列，等待RGV小车搬运即视为托盘排队，等候RGV小车服务，搬运到指定站台，视为服务结束。

模型约束松弛条件的建立：

1）托盘的到达是无限且相互独立的，到达时间服从泊松分布。

2）排队规则为等待制，即托盘排队等待直到被搬运完成。

3）服务过程为先到先服务服务方式。

4）环轨上有7台RGV小车，即系统有7个服务窗口进行服务。

5）RGV小车服务时间服从负指数分布。

由约束松弛条件可知B厂环形RGV系统属于多服务窗等待制M/M/n排队模型，如图3所示。

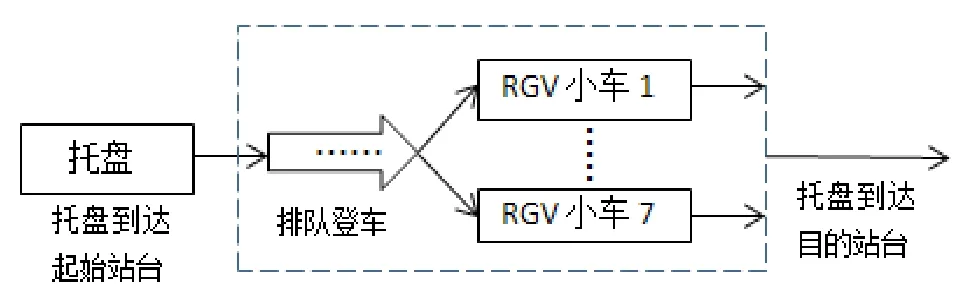
图3 B厂环形RGV系统排队模型框图

设托盘到达规律服从参数为λ的泊松过程，RGV小车服务时间服从参数为μ的负指数分布，考虑到环形轨道上多车间存在任务调度及前后车安全防撞距离保护等因素，其整体服务效率为η，参照排队论M/M/n模型的计算方法[3]，则系统服务强度为：

系统内所有RGV小车都空闲的概率：

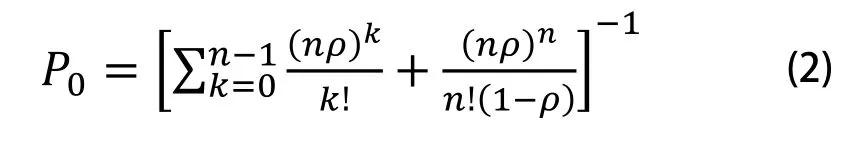
系统中托盘的平均等待队长为：

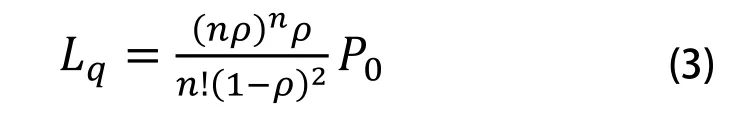
系统中托盘的平均等待时间：

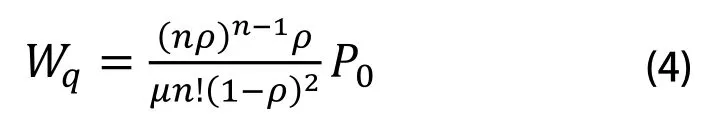
平均正在服务的RGV小车台数：

2 应用实例分析

如表1所示，B厂环形RGV系统相关参数可知，每托盘的出入库时间：站台与RGV小车交接托盘一次所需时间：托盘到达时间即为t1与t2之和，因此，托盘到达率为：=0.0328。RGV小车完成一次搬运服务的时间即RGV小车在轨道上行驶时间和两次交接托盘时间之和，此处RGV小车采用规则调度，环轨一圈一次入库一次出库，一个周期时间直道和弯道时间减半，所以T+2t2=151.38秒。服务率即为：环轨RGV小车数量n=7，取0.8。将实际数据带人以上公式，可以计算B厂环形RGV系统排队模型的运行指标，如下：

1）系统服务强度：

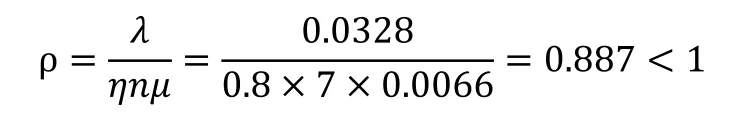
2）系统内所有RGV小车都空闲的概率：

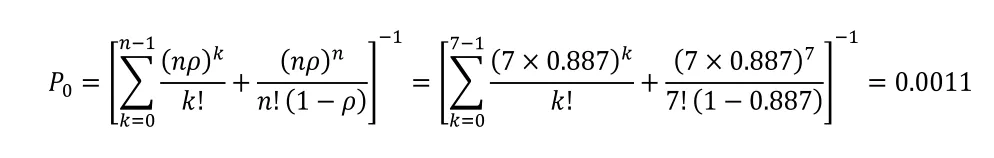
3）系统中托盘的平均等待队长为：

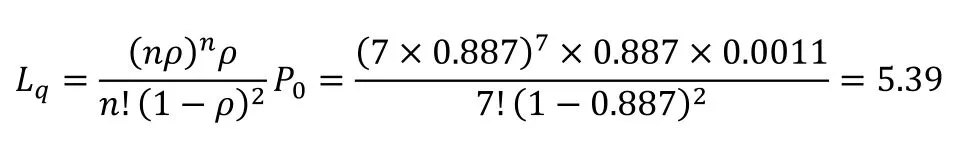
4）系统中托盘的平均等待时间：

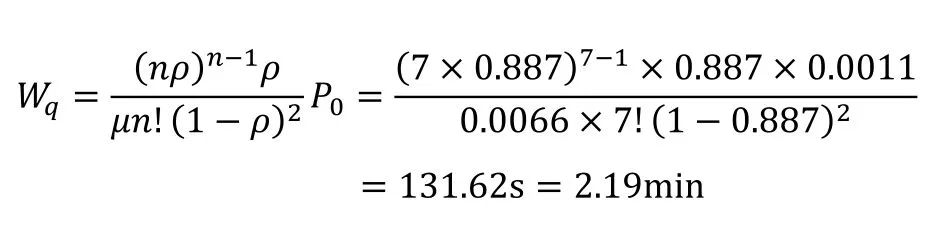
5）平均正在服务的RGV小车台数：

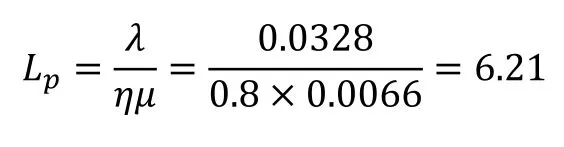
6）环形RGV系统运行效率：

对排队论模型计算出的环形RGV系统各性能指标进行分析：

系统服务强度为0.887，小于1，托盘的平均等待队长为5.39，小于系统处于稳态时所需的平均等待队长（其值取站台最大缓存W值的一半：）[4]，说明该系统较为稳定；RGV小车平均正在服务台数为6.21，说明RGV小车空闲率较低；平均等待时间为2.19min，远小于RGV小车绕行环轨一圈的时间4.51min，说明托盘平均等待时间较短；RGV系统运行效率为88.7%，说明系统运行效率较高。通过以上各性能指标的分析，论证了该环形RGV系统设计较为合理，满足了用户的需求。

3 结束语

排队论在对随机系统的分析中，是一个很好的数学工具。通过此数学工具，可以对系统的状态进行分析，继而指导系统的评估和优化。本文以排队论为基础，结合项目实际运行参数，对B厂环形RGV系统进行了排队论数学模型的抽象和系统各主要性能指标参数的求解，并且对其结果进行了分析和评估，具有非常重要的实际意义，为环形RGV系统或类似系统的评估和优化提供了一种便捷有效的方法。

[1]顾红,邹平,徐伟华.环形穿梭车优化调度问题的自学习算法[J].系统工程理论与实践,2013.12.

[2]李斌,吴双,匡永江.仓储物流系统中多车同轨模型的控制方法研究[J].制造业自动化,2008,30(4):20-22.

[3]孙荣桓,李建平.排队论基础[M].北京:科学出版社,2002.

[4]杨少华,张家毅,赵立.基于排队论的环轨多车数量与能力分析[J].制造业自动化,2011.08.

[5]董皓,张伟,朱德桥,岳琦.基于排队论理论的自动化立体仓库系统运行参数分析[J].机械设计与制造,2010.06.