基于边缘保持的医学超声图像滤波方法

陈文山

（福建卫生职业技术学院，福州 350101）

0 引言

因为超声成像具有安全性、实时性和廉价性的特点，在临床诊断中广泛应用。在超声诊断中希望通过三维分割[1]、三维重建[2]，从而更全面获取目标腔体整体信息。由于超声图像存在独有的斑点噪声，为提高三维分割效率，希望在尽可能保护边缘的前提下对超声图像进行滤波。

目前经典的图像增强滤波方法基本上可分为两大类：空域处理法和频域处理法。然而，线性滤波能够有效去除噪声，但同时会使图像的边界模糊；中值滤波能有效去除脉冲噪声，但因为窗口内的排序处理破坏了空间相邻信息和结构，所以在去除噪声的同时使图像细节丢失、棱角模糊。基于各项异性扩散方程的滤波方法可以去除噪声、边界保留，但由于各向异性扩散实质上为迭代过程，要通过多次迭代，计算量大，运算速度慢。

考虑到后续在超声图像三维重建的应用需要，希望寻求一种有效去除噪声的同时又不丢失边缘信息，并且具有较高运算速度的超声图像滤波算法。本文在各向异性扩散方程的基础上，结合中值滤波高效滤除斑点噪声，各向同性扩散方程在图像同质区域高速扩散的特点，根据图像梯度，设计一种基于边缘保持的医学超声图像滤波方法。

1 算法原理及实现方法

1.1 扩散方程模型

图像处理中的各向异性扩散理论源于对流体扩散分析的类比研究[3]。它将图像灰度值I看作流体中的溶质，根据热扩散理论，为了使浓度高的溶质和其周围区域达到一种平衡，溶质会向周围区域扩散，扩散方程为在这里，D为扩散张量（即扩散系数），∂t为对时间的导数。各向异性扩散方程实质为具有各项异性扩散系数的偏微分方程，而对各向异性扩散方程的迭代过程就是求解初始值为输入图像的偏微分方程。

1.1.1 各向同性扩散模型（常系数热传导方程模型）

Marr等人将原图像u0（x，y）与几个带不同参数σ的高斯核Gσ（x，y）作卷积，得到该图像在若干尺度下的平滑图像u（x，y）。各向同性扩散模型在图像的平滑过程中具有两个特性：1）当尺度由小变大时，图像的平滑效果增强，图像的细节特征逐渐消失；2）在大尺度上保留的图像特征，其空间位置会展宽并发生漂移，使图像的边界、端点模糊。

1.1.2 各向异性扩散模型

由于各向同性扩散模型在平滑图像的同时也破坏了图像的一些重要的信息特征。为了克服其缺点，Perona和Malik给出了各向异性扩散模型。与各向同性扩散方程模型相比较，它实际上是一非线性抛物型微分方程。因其扩散速度随着梯度模的不同而改变，所以该模型为各向异性扩散。然而，当图像含有的噪声梯度较大时，异性扩散模型对噪声无法去除，带有噪声的边界也会被破坏。

1.2 基于边缘保持的医学超声图像滤波方法

针对医学超声图像噪声大且在不同区域内有不同的噪声模型，而用于三维分割的图像数据量大、对边缘保持要求高的特点[4]，本文以图像像素点梯度Y为阈值，采用综合滤波方法。当像素点梯度Y较大时，对图像进行中值去噪，去除高梯度噪声；当像素点梯度Y较小时，对图像进行各向异性扩散，去除噪声同时保持边界；其余部分，对图像进行各向同性扩散，去除随机噪声，提高滤波速度；

综合滤波方法具体模型如下：

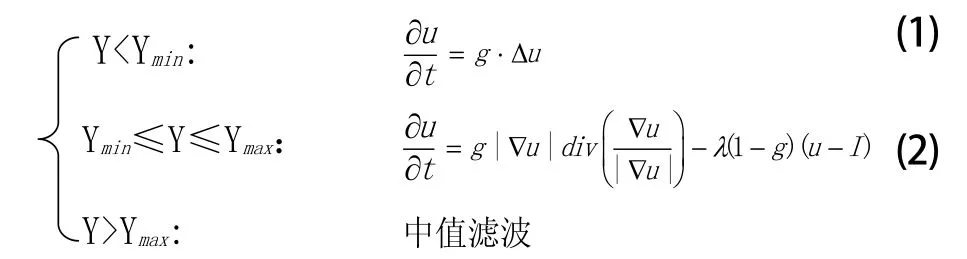
其中，Δu是各向同性的拉普拉斯算子；∇u是∇u(x,y,t))的简写，代表梯度算子；div是散度算子；是起扩散滤波作用的退化扩散项；u是当前迭代的图像，I是原始图像，(1-g)(u-I)是保持初始图像不过度扩散的平衡控制项；g是用来检测边界和控制扩散速度的尺度函数。Gσ是高斯函数，在此作为卷积算子对图像进行平滑滤波。

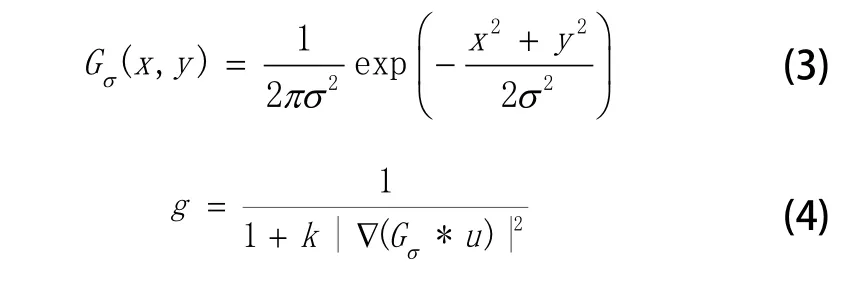
1.2.1 g函数的去噪原理

g函数在模型中起着增强边界并控制扩散速度的作用。当图像灰度差小时，梯度∇(Gσ*u(x,y,t))表现得小，此时g函数接近于1，退化扩散项充分发挥作用，扩散幅度加大，噪声被平滑。当图像灰度差大时，梯度∇(GGσ*u(x,y,t))表现得大，此时g函数接近于0，退化扩散项被控制，边缘得到增强。

1.2.2 退化扩散项的去噪原理

退化扩散项是本文模型的核心，它有选择的在图像边缘的切线上对图像进行扩散滤波，在消除图像噪声的同时又增强了图像的边界。扩散滤波是在边缘的切线方向和梯度方向上的异性扩散，因而对边缘的保护作用有限；而退化扩散滤波只在边缘的切线方向上扩散，而在梯度方向上不扩散，从而对边缘起到保护乃至增强的作用。

1.2.3 边缘保持因子k的取值

由g函数的定义，知g函数由图像高斯卷积后的梯度和常数k共同决定。前者由当前处理的图像决定，后者需要人为设定。考虑到g函数的作用主要是限制退化扩散项的扩散行为，防止高梯度的图像边界被扩散项破坏，而对于较低梯度的图像同质区，扩散项的滤波功能应该充分发挥。实验证明，对于带有大量噪声的医学超声图像，g函数能够更彻底的滤除噪声，同时减少迭代次数从而节约了图像处理时间。

1.2.4 平衡控制项原理

控制项具有使扩散结果保持与原图像重要信息一致的功能。它在合适的程度上降低了扩散滤波对图像信息的负面影响，但效果不甚理想。控制项和扩散项之间的平衡由式子(1-g)控制。随着(1-g)值的变化，模型会在图像的不同位置呈现不同的效果：在同质区域内部，较小，g～1，模型有较强的扩散作用；在尖锐处，例如边缘，g～0，(1-g)～1，平滑后的图像u会和原始图像I保持一致。λ值在此处有调整平衡控制项功能的作用：λ值越大，原始图像信息保持得越完整，但滤波效果越有损耗。考虑到效率问题，本论文中一般取λ=1。

1.2.5 中值滤波及阈值选择

本文模型中每次退化扩散滤波前对图像进行的高斯滤波具有一定的平滑噪声的作用。然而实践中，仅使用“退化扩散项＋平衡控制项”存在两个问题：1）高斯函数参数σ不易控制，模型不稳定；2）模型对边缘选择性增强，迭代完成后图像边界出现因过度增强产生的亮斑，在图像同质区域会产生新的细小散斑。本文设想引入中值滤波滤除随机散粒噪声。散粒噪声点处局部梯度模具有较大值。当局部梯度的模大于某个阈值时，在该点采用中值滤波；对于大部分局部梯度模小于阈值的像素点，依然采用各向异性扩散。这样不但去除噪声，还能保持边缘。实验中，图像处理前由于大量噪声的影响，代表图像平滑的同质区域小，代表噪声的中等梯度区域大；图像处理后噪声被平滑，代表噪声的中等梯度概率变小，代表图像平滑的同质区域大量增加，代表边界的高梯度区依然保留。当阈值过大时，中值滤波的作用无法发挥；当阈值过小时，对图像边界有模糊作用且会有新的噪声产生。经过反复实验，本文取经验值Ymax=120作为阈值。实验结果表明，引入中值滤波后，由于中值滤波对模型降噪作用的增强，处理图像的迭代次数有所下降，缩短了图像处理时间，提高了处理速度。

1.2.6 各向同性扩散及阈值选择

扩散方程扩散滤波中提到了拉普拉斯算子因为它从图像边缘的切线方向和梯度方向同时等大地进行扩散，所以被称为各向同性扩散。各向同性扩散不能保留边界，但对同质区域内的低梯度随机噪声有良好效果，更关键的是因为其运算相对简单，它可以有效提高图像处理的速度。随着迭代次数的增加，低梯度的图像区域明显增加，而图像梯度的变换也主要集中在低梯度区。这便从理论上说明了各向同性扩散的阈值选择也可以固定为一个很小的常数。实验证明，Ymin在0.5到1之间取值时，不但可以提高模型的速度，还可以配合中值滤波有效地改善因为退化扩散造成地边缘亮斑和随机散斑。当Ymin取值过小时，各向同性滤波地效果不明显；当Ymin取值过大时，图像会产生雾状噪声。

1.2.7 迭代终止准则

方程迭代终止时间T的确定对扩散方程滤波的结果有很大影响：如果T过小，则迭代的结果对初值图像有很大的依赖性，使得图像的很多噪声不能被滤除；如果T过大，则迭代的结果就会被扩散方程中固有的动力学特征所主宰，不但浪费了时间，还会对图像产生负效果。所以一个高效低计算量的迭代终止准则对于模型的计算机实现是相当必要的。当图像迭代不完全时，前后图像间的变化大，当图像迭代基本完成后，前后图像间的变化会极小。本文设想根据前后图像间变化定义迭代终止准则ISC，当ISC满足小于一定阈值时，图像自适应地停止迭代。

2 实验结果及分析

为了对本算法的有效性进行验证，实验中选取了大量对比度较低，视觉效果较差[5]的医学超声图像。图1为其中一幅左心室声像图。

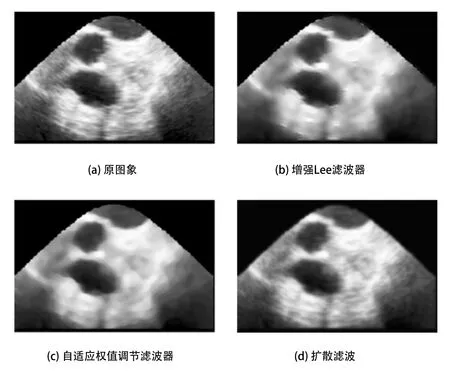
图1 心脏超声图像实验结果

图1(a)是原图像，图1(b)是增强Lee滤波器处理的图像，图1(c)是自适应权值调节滤波器处理的图像，图1(d)是扩散滤波处理的图像，图1(e)是各项异性扩散滤波处理的图像，图1(f)是本文模型处理的图像。通过对比可知，图1(b)、图1(c)、图1(d)的滤波方法[6]，虽然一定程度上滤除了噪声，但是整个图像的清晰度有了明显下降，轮廓也变得比较模糊。图1(e)各项异性扩散滤波处理后的图像效果良好，既滤除了噪声边缘也得到了很好的保留。图1(f)本文模型在达到上述效果的基础上，还对边缘起到了一定的锐化作用，本文模型在超声图像的去噪、保护边缘上具有独特的优势，不但能够快速有效地消除噪声，还能有效增强边缘，同时边缘的保持也与原始图像最为吻合，边缘线条更加平滑自然。边缘信息的保护对超声医学图像诊断具有十分重要的意义。

3 结论

大量实验结果表明，考虑图像的梯度分布特征后，改进的基于边缘保持的医学超声图像滤波方法，较现有的图像滤波方法在滤除超声图像时具有更好地保护图像边缘、保留图像细节信息的特点，是一种有效的医学超声图像滤波方法。

[1]陈文山.基于曲面形变模型的心脏超声图像三维分割[J].福建电脑.2011(9):96-97.

[2]陈文山.基于三角网格模型的心脏超声图像三维表面重建[J].福建电脑.2014(11):20-22.

[3]Jemila Rose R,Allwin S. Denoising of Ultrasound Cervix Image Using Improved Anisotropic Diffusion Filter.[J].The West Indian medical journal,2015,64(4).

[4]陈文山.基于局部分形维数特征的医学超声图像轮廓提取[J].福建电脑.2014(10):24-25.

[5]陈文山,汪天富,林江莉.基于相似度测量的医学超声图像对比度增强[J].中国医学影像技术.2006(9):1432-1434.

[6]Qingzheng Wang,Shuai Li,Hong Qin,Aimin Hao. Robust multimodal medical image fusion via anisotropic heat diffusion guided low-rank structural analysis[J].Information Fusion,2015,26.