飞片撞击冲击波载荷在液舱中的弥散效应

赵延杰，汪俊，郝轶，张伦平，刘建湖

1中国船舶科学研究中心，江苏无锡214082

2国防科技工业海洋防务技术创新中心，江苏无锡214082

0 引 言

由于受反舰武器等攻击威胁较大，大型水面舰船通常设置专门的舷侧防护结构来抵御水下接触爆炸。常规的舷侧防护结构从外至内为“空舱—液舱—空舱”的布置形式，充分利用空间、介质和结构实现对内部重要舱室的防护。其中最外侧空舱通过结构破坏来消耗、缓冲和阻击高频强爆炸载荷，中部液舱通过内部液体来吸收、弥散压力波载荷及飞片载荷，内侧空舱提供变形空间并进行水密。为了合理设计中部液舱，使其经济、高效地吸收并弥散爆炸载荷，必须获得爆炸载荷在液舱内的衰减规律。飞片传递到液舱的爆炸载荷包括爆炸冲击波，以及外侧空舱破坏产生的飞片进入液舱产生的压力波载荷。国外关于液舱对爆炸冲击波载荷和飞片载荷衰减作用的研究较少。Lee等［1］基于势流理论推导了球形弹体高速入水过程形成空穴和初始压力波的理论公式；Nishida等［2］针对球形弹侵彻封闭液舱予以了研究，发现激波能占飞片初始动能的很小一部分，但是较低的飞片速度不能模拟爆炸产生的高速飞片对结构的破坏作用；Townsend等［3］开展了弹体高速打击液舱的实验，获得了液舱中空气层对压力波和舱室破坏的影响。在国内，唐廷等［4］运用一维平面波理论，推导了大质量飞片初始冲击波的理论公式，并结合仿真计算分析了飞片特性对冲击波的影响；唐廷等［4］和孔祥韶等［5-6］对单发飞片和双发飞片同时穿透液舱的过程进行了数值计算，分析了飞片速度的衰减规律、液舱内板的响应及舱内液体中冲击波压力的叠加效应，结合Wen-Jones模型提出了以液舱内板的极限穿透速度为判据的液舱防御飞片有效性的分析方法；张伟等［7］利用一级氢气炮高速发射弹体水平入水试验获得了冲击波压力峰值的衰减特性，发现压力峰值在波的传播方向满足指数衰减特征，压力曲线介于距离的倒数与距离平方的倒数曲线之间；李思宇等［8］对液舱内有无液体、不同厚度比和不同水层厚度条件下液舱各部分吸能占比情况开展了数值仿真研究；沈晓乐等［9］针对爆炸飞片侵彻防护液舱进行了试验研究，认为高速撞击会产生墩粗和侵蚀，导致飞片速度较高时其侵彻深度反而下降；李营［10］研究了飞片侵彻液舱过程中的能量吸收机理，并对飞片入水形成的压力波机理进行了理论分析。

本文拟重点关注飞片在液舱中运动时产生的初始冲击波载荷及其弥散规律，开展飞片作用小型液舱机理性试验，计算实尺度液舱对飞片撞击冲击波载荷的弥散作用。

1 飞片作用小型液舱机理性试验

利用水箱模拟小型液舱，采用7个高精度雷管同步起爆的方式，爆轰驱动圆形飞片，在飞片撞击水箱时测量水箱前板的壁面压力和水箱中的自由场压力，得到飞片压力波在液舱中的衰减规律。水箱尺寸为700 mm×700 mm×700 mm，采用Q235钢制作，试验时水箱内装满水。试验工况见表1，测点布置与测点见图1和表2。飞片速度和入射角经过大量的预试验标定后确定。在预试验中，速度采用多普勒光纤探针（DPS）探头测试，误差不超过±5%，入射角采用撞击标准靶板时靶板背面大量电探针的导通时刻来判读。

表1 试验工况Table 1 Experiment case

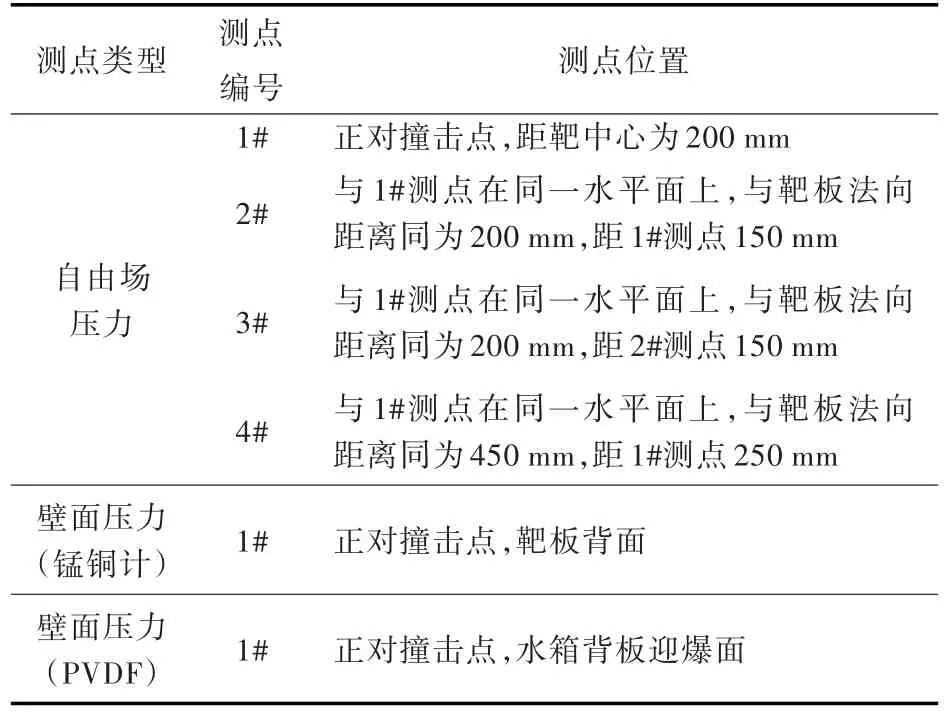
表2 试验模型测点Table 2 Measuring points of the model

分别测量了靶板背面壁面压力（锰铜计）和水箱中自由场压力的时程曲线。试验结果如表3所示。在自由场压力测量中，由于传感器供电压力不足，当压力峰值大于27 MPa时，压力时程曲线出现平头现象，无压力峰值。锰铜计和压电聚偏氟乙烯高分子薄膜（PVDF）测量结果只在表3中给出峰值。图2和图3分别给出了2次重复试验获得的自由场压力时程曲线。

表3 压力峰值试验结果Table 3 Experimental results of pressure peak

2 数值仿真计算

采用显式动力分析软件AUTODYN对上述试验进行数值仿真研究。为减小计算量，建立二维轴对称计算模型。计算模型的范围与机理性试验模型保持一致。在计算过程中，忽略飞片撞击液舱前壁板的过程，按照动量守恒定律，对飞片的质量和速度进行修正。飞片由左侧飞入水层，水层右侧边界模拟试验中的水箱后壁板，厚6 mm。飞片和水箱后壁板采用拉格朗日单元建模，水和空气采用欧拉单元建模。拉格朗日单元和欧拉单元的尺寸均为1 mm。计算模型和边界条件见图4。

水采用冲击状态方程描述，空气采用理想气体状态方程描述，钢采用Johnson-Cook模型及失效准则。材料参数的取值见表4～表6。

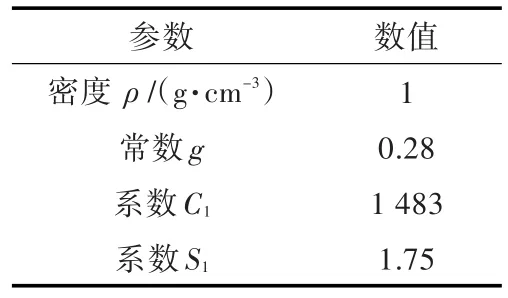
表4 水的状态方程参数Table 4 Parameters in state equation of water

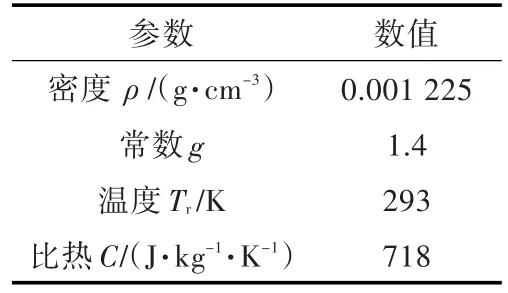
表5 空气的状态方程参数Table 5 Parameters in state equation of air

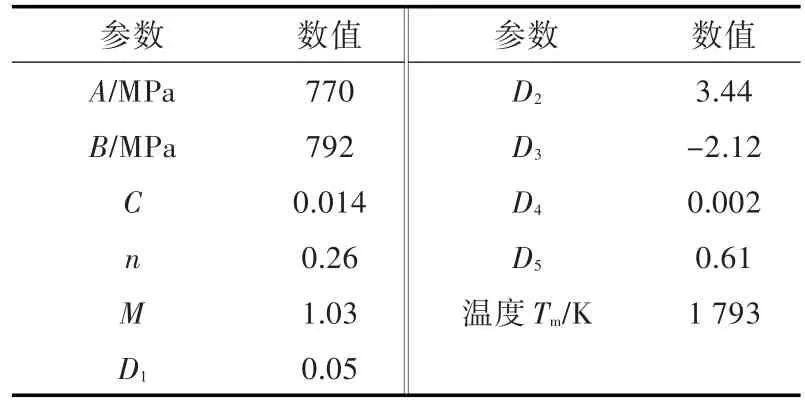
表6 钢的材料参数Table 6 Parameters in Johnson-Cook model of steel

在数值计算中，修正后的飞片（厚度为12 mm，初速度v0=750 m/s）从空气中飞入液舱。计算模型中压力测点布置如图5所示，其中，在计算模型轴线上沿入射方向布置1#～15#测点，间距为50 mm；在9#测点所在纵向位置由轴线向边界布置16#～21#测点，间距为50 mm；在5#测点所在纵向位置由轴线向边界布置22#～28#测点（22#与5#测点位置重合），间距为50 mm；在15#测点所在纵向位置由轴线向边界布置29#～33#测点（29#与15#测点位置重合），间距为50 mm。

图6和图7分别给出了工况1-1中4#测点以及工况1-2中3#测点的试验与仿真对比结果。图7中，试验曲线的第2个压力峰值由冲击波在水箱侧壁的反射造成，仿真中因未考虑水箱侧壁面，故未能出现第2个峰值。由图可以看到，对于自由场压力，采用数值仿真方法可以较好地模拟压力峰值及波形。

表7给出了不同工况下的压力峰值对比结果。由表可见，3#和4#测点的自由场压力峰值计算值与试验值误差较小，约为5%；锰铜计和PVDF测得的压力峰值与计算值的误差较大，这是由于：1）计算时未考虑飞片对水箱前壁板的碰撞作用，导致锰铜计所在位置的计算值偏小；2）试验时PVDF测点处的压力被自由场压力传感器遮挡，导致试验值偏小。

表7 压力峰值对比结果Table 7 Comparison of pressure peak

虽然有效数据较少，但从自由场压力计算结果来看，本次数值仿真采用的算法精度较高，可用于后续液舱内载荷弥散的分析计算。

3 实尺度液舱对飞片载荷的弥散作用分析

按照大型水面舰船舷侧液舱的实际尺度建立计算模型，分析单个飞片撞击液舱并在液舱中运动时压力波载荷的弥散规律。为减小计算量，仍采用二维轴对称计算模型，模型示意图及主要尺度参数如图8所示。计算水域（轴对称模型）宽1.6 m，高3.9 m，前、后各有厚度为0.1 m的空气层。在计算过程中，忽略飞片撞击液舱前壁板的过程，按照动量守恒定律对飞片的质量和速度进行修正。修正后的飞片直径为420 mm，厚度为22 mm，初速度为923 m/s。

采用与第2节相同的材料参数及边界条件。图8给出了实尺度液舱计算模型中压力测点的布置，其中，在计算模型轴线上沿入射方向布置1#～17#测点，间距为100 mm；在1#测点所在纵向位置由轴线向边界布置18#～36#测点，间距为200 mm（其中18#与1#测点的间距为100 mm）；在5#测点所在纵向位置由轴线向边界布置37#～55#测点，间距为200 mm（其中37#与5#测点的间距为100 mm）；在9#测点所在纵向位置由轴线向边界布置56#～74#测点，间距为200 mm（其中56#与9#测点的间距为100 mm）；在13#测点所在纵向位置由轴线向边界布置75#～93#测点，间距为200 mm（其中75#与13#测点的间距为100 mm）；在17#测点所在纵向位置由轴线向边界布置94#～112#测点，间距为200 mm（其中94#与17#测点的间距为100 mm）。

图9给出了飞片在液舱中的运动过程。在t=0.037 ms时，飞片刚刚进入液舱，受到水的拍击作用，产生塑性变形，如图9（a）所示；飞片的高速运动导致其后部产生空穴，随着飞片向液舱内部运动，空穴尺寸不断变大，同时由于飞片中部所受阻力较边缘更大，飞片在运动过程中的形态逐渐演变为一个反帽型结构，如图9（b）～图9（e）所示；受舱内液体的阻力作用，飞片速度迅速衰减，同时其后部的空穴开始闭合，如图9（f）～图9（h）所示。

图10给出了压力波在液舱内的传播过程。在t=0.037 ms时，飞片刚进入液舱，压力峰值达到2.82 GPa，如图10（a）所示；随后,压力峰值迅速衰减，当压力波波阵面进入液舱内部约200 mm时，压力峰值降至2 GPa，当压力波波阵面进入液舱内部约600 mm时，压力峰值降至0.45 GPa，如图10（b）～图10（c）所示；在初始压力波之后，飞片在液舱中继续运动还会形成二次压力波，不过二次压力波的峰值较初始压力峰值低了1个量级，如图10（d）～图10（e）所示；在0.9 ms时，初始压力波到达液舱内壁，此时压力峰值衰减至0.1 GPa，在垂直于飞片运动方向的压力峰值的衰减速度明显快于飞片运动方向的，如图10（f）所示。

图11所示为飞片的速度时程曲线。由图可见，刚入水时飞片速度迅速衰减，在0.2 ms时降至400 m/s以下，随后，飞片速度缓慢衰减，至2.5 ms时速度降至168 m/s左右。这是因为飞片在水中运动时受到的阻力与其自身速度相关，速度越大，阻力也越大，故前期速度衰减较快。

3.1 压力峰值衰减规律

图12给出了飞片入射轴线上典型测点的压力时程曲线和压力峰值P衰减规律，各测点的间距为400 mm。从中可以看到，在飞片入射轴线上，各测点的压力峰值迅速衰减，且从拟合的压力峰值衰减曲线来看，压力峰值呈幂函数衰减规律。

图13给出了与飞片入射轴线成45°方向典型测点的压力时程曲线和压力峰值衰减规律。其中2#与38#测点的间距为424 mm，38#与59#测点以及59#与80#测点的间距为565 mm。由图可以看到，在斜45°方向压力峰值也迅速衰减，从拟合的峰值衰减曲线来看，压力峰值亦呈现函数衰减规律。

图14～图16分别给出了5#，9#和13#测点所在纵向位置处典型测点的压力时程曲线和压力峰值衰减规律。从中可以看到，在5#测点的纵向位置，压力峰值由中心轴线向侧面呈幂函数衰减规律；在9#测点的纵向位置，压力峰值由中心轴线向侧面呈指数衰减规律，且其衰减速率明显低于5#测点纵向位置处；在13#测点的纵向位置，压力峰值由中心轴线向侧面呈线性衰减规律，衰减速率较5#和9#测点纵向位置处的更低。出现这种衰减规律的原因是：压力波在整个流场中衰减非常迅速，在飞片入射点附近压力峰值衰减较为显著，而在远离飞片入射点的位置压力峰值普遍较低，故衰减速率也降低了。

图17为整个计算区域压力峰值的分布情况。图17（a）为压力峰值的三维曲面图及投影，与前述分析类似，在飞片入射点附近压力峰值较高，随后压力峰值在飞片入射方向及其他方向迅速衰减，在距离入射点800 mm时，压力峰值降至入射点压力峰值的1/10左右。图17（b）为拟合得到的压力峰值衰减规律曲面及拟合公式，沿飞片入射方向和垂直入射方向，压力峰值按照指数衰减规律进行拟合，得到的方差R2=0.96，可见本文给出的拟合公式能够较准确地反映压力峰值的衰减规律。

3.2 冲量衰减规律

采用与3.1节类似的方法分析计算域内冲量I的衰减规律。需要说明的是，为消除水中压力自由面反射和壁面反射的影响，对各测点的冲量计算仅限于压力波的第1个脉冲。

图18为飞片入射轴线上典型测点的冲量衰减规律，各测点的间距为400 mm。从中可以看出，在飞片入射轴线上，各测点的压力峰值迅速衰减，拟合的压力峰值呈幂函数衰减规律。

图19为与飞片入射轴线成45°方向典型测点的冲量衰减规律，2#与38#测点的间距为424 mm，38#与59#测点以及59#与80#测点的间距为565 mm。可以看出，在斜45°方向，压力峰值也迅速衰减，拟合的压力峰值亦呈幂函数衰减规律。

图20～图22分别为5#，9#和13#测点所在纵向位置处典型测点的冲量衰减规律。可以出，在5#测点所在纵向位置，压力峰值由中心轴线向侧面呈指数衰减规律；在9#和13#测点所在纵向位置，压力峰值由中心轴线向侧面均呈现出线性衰减规律，可见，与峰值压力相比，冲量的衰减较为温和，衰减速率低于峰值压力的衰减速率。

图23为整个计算区域的冲量分布情况。图23（a）为冲量的三维曲面图及投影，与前述分析类似，在飞片入射点附近冲量值较大，随后，冲量在飞片入射方向及其他方向迅速衰减。从云图看，冲量在飞片入射方向衰减最慢，在其他方向衰减快一些；在飞片入射方向，距离入射点1 300 mm处的冲量降至飞片入射点冲量的1/10左右，这说明冲量的衰减较压力峰值更为缓和。图23（b）给出了拟合得到的冲量衰减规律曲面及拟合公式，与峰值压力的拟合类似，沿飞片入射方向和垂直入射方向的冲量衰减均按指数衰减规律来拟合，得到的拟合方差为R2=0.905，可见拟合公式能较准确地反映冲量衰减规律。

4 结 论

本文通过开展飞片撞击小型液舱的机理性试验和数值仿真研究，获得了飞片压力波载荷在液舱内的衰减规律，主要结论如下：

1）在数值计算中忽略飞片撞击液舱前板的过程，对飞片的质量和速度按动量守恒定律进行修正是合理的；本文采用的二维轴对称计算模型可以较准确地模拟液舱中飞片运动产生的压力波载荷。

2）飞片进入液舱时产生的初始压力波的压力峰值可达GPa级，在水中运动产生的二次压力波的压力峰值比初始压力波的低1个量级。

3）飞片在水中运动时，中部所受阻力比边缘的大，故其运动形态逐渐演变为一个反帽型结构。

4）压力峰值及冲量由飞片入射点开始迅速衰减，在飞片入射方向及斜45°方向呈幂函数衰减规律，随着纵向位置远离飞片入射点，压力峰值及冲量在纵向的衰减趋于缓和；整体来讲，冲量的衰减较压力峰值更为缓和；压力峰值和冲量在整个流场中符合指数衰减规律。

［1］LEE M，LONGORIA R G，WILSON D E.Ballistic waves in high-speed water entry［J］.Journal of Fluids and Structures，1997，11（7）：819-844.

［2］NISHIDA M，TANAKA K.Experimental study of perforation and cracking of water-filled aluminum tubes impacted by steel spheres［J］.International Journal of Impact Engineering，2006，32（12）：2000-2016.

［3］TOWNSEND D，PARK N，DEVALL P M.Failure of fluid dilled structures due to high velocity fragment impact［J］.International Journal of Impact Engineering，2003，29（1-10）：723-733.

［4］唐廷，朱锡，侯海量，等.高速破片在防雷舱结构中引起的冲击荷载的理论研究［J］.振动与冲击，2013，32（6）：132-136，148.TANG T，ZHU X，HOU H L，et al.Shock loading induced by high speed fragment in cabin near shipboard［J］.Journal of Vibration and Shock，2013，32（6）：132-136，148（in Chinese）.

［5］孔祥韶，吴卫国，李俊，等.爆炸破片对防护液舱的穿透效应［J］.爆炸与冲击，2013，33（5）：471-478.KONG X S，WU W G，LI J，et al.Effects of explosion fragments penetrating defensive liquid-filled cabins［J］.Explosion and Shock Waves，2013，33（5）：471-478（in Chinese）.

［6］孔祥韶，吴卫国，刘芳，等.舰船舷侧防护液舱对爆炸破片的防御作用研究［J］.船舶力学，2014，18（8）：996-1004.KONG X S，WU W G，LIU F，et al.Research on protective effect of guarding fluid cabin under attacking by explosion fragments［J］.Journal of Ship Mechanics，2014，18（8）：996-1004（in Chinese）.

［7］张伟，黄威，任鹏，等.高速弹体水平入水产生冲击波特性［J］. 哈尔滨工业大学学报，2016，48（4）：37-41.ZHANG W，HUANG W，REN P，et al.The underwater shock wave characteristics caused by high speed horizontal water entry projectiles［J］.Journal of Harbin Institute of Technology，2016，48（4）：37-41（in Chinese）.

［8］李思宇，李晓彬，赵鹏铎，等.近爆载荷作用下液舱的吸能研究［J］.中国舰船研究，2017，12（1）：101-106，133.LI S Y，LI X B，ZHAO P D，et al.Research into energy absorption of liquid cabin subjected to close-range explosion［J］.Chinese Journal of Ship Research，2017，12（1）：101-106，133（in Chinese）.

［9］沈晓乐，朱锡，侯海量，等.高速破片侵彻防护液舱试验研究［J］.中国舰船研究，2011，6（3）：12-15.SHEN X L，ZHU X，HOU H L，et al.Experimental study on penetration properties of high velocity fragment into safety liquid cabin［J］.Chinese Journal of Ship Research，2011，6（3）：12-15（in Chinese）.

［10］李营.液舱防爆炸破片侵彻作用机理研究［M］.武汉：武汉理工大学，2014.LI Y.Fragment resistant mechanism research of safety liquid cabin［M］.Wuhan：Wuhan University of Technology，2014（in Chinese）.