基于汛期分期的洪峰流量特征研究
2018-06-22莫崇勋黄怡婷何嘉奇孙桂凯阮俞理
莫崇勋,黄怡婷,何嘉奇,孙桂凯,阮俞理
(1.广西大学土木建筑工程学院,广西南宁530004; 2.工程防灾与结构安全教育部重点实验室,广西南宁530004; 3.广西防灾减灾与工程安全重点实验室,广西南宁530004)
0 引 言
据统计,1950年~2016年我国平均每年因水灾造成直接经济损失1 481.62亿元,因旱灾造成直接经济损失922.71亿元[1]。我国是洪水和干旱频发的国家,并且水资源的这种矛盾性给人民的生命财产安全造成了严重的损失。近年来,利用洪水资源解决区域水资源紧缺问题成为全球热议的话题。我国在汛期分期方面的研究成果丰硕,但在汛期分期的研究中,缺少对分期洪水特征(趋势性、突变性和周期性)方面的研究。在当今全球气候变化的背景下,洪水的演变规律可能发生了改变。为了能更准确地了解洪水的变化规律、合理地对水库汛限水位进行动态调控、充分地利用洪水资源,对分期洪水特征进行研究是非常有必要的。
目前,研究序列特征的方法有很多种,如累计距平法、线性倾向估计法、Mann-Kendall检验法、线性回归法、Spearman秩序相关检验法和小波分析法等。陈磊等[2]利用Mann-Kendall和累计距平法研究黄河流域季节性降水的变化趋势和变异情况,从而得到了该流域季节性降水在时间和空间上的变化规律;刘增进等[3]利用滑动平移、小波分析等方法对霞曲流域1956年~2010年降水趋势进行分析,进一步确定了该流域降水的趋势性、突变性和周期性;张应华等[4]对研究水文气象序列趋势和变异特性常用的方法进行了详细的介绍;普发贵[5]运用Mann-Kendall检验法对抚仙湖主要水质指标的变化特征进行分析。但对分期条件下各分期洪峰流量序列的研究还鲜有涉及。鉴此,本研究在已有的龙滩水库汛期分期成果[6](前汛期:4月1日~6月7日;主汛期:6月8日~9月1日;后汛期:9月2日~10月31日)基础上,用滑动平均法、累计距平法、Mann-Kendall检验法和小波分析,对1960年~2012年分期后龙滩水库前、主和后汛期洪峰流量的趋势、突变和周期特征进行研究。期冀为当地水库汛期管理工作提供科学依据。
1 研究区域概况
红水河发源于云南省东部沾益县马雄山,位于广西壮族自治区西北部,是珠江干流西江水系的主要干流。红水河干流全长1 573 km,流域多年平均径流量为696亿m3,多年平均径流深为543.1 mm(红水河在天峨县境内多年平均径流量达到499.1亿m3,多年平均径流深543.1 mm)。据调查,红水河汛期一般在4月~9月,占年径流总量的78.2%。其中,最大径流量在7月,可达到141亿m3,最枯流量在3月,只有12.6亿m3。
龙滩水库位于红水河上游广西壮族自治区天峨县境内,以发电为主,同时兼顾防洪、航运、水资源配置的功能等。龙滩水库坝址控制流域面积为9.85万km2,占红水河流域面积的75.3%,多年平均径流量为508亿m3。
2 研究方法
2.1 滑动平均法
滑动平均法是一种从n项序列中计算多个连续m项(m (1) 式中,t为经滑动平均后的序列项,t 累计距平法是一种通过曲线直观判断离散数据点变化趋势的方法[4]。当累计距平曲线呈上升趋势则表示距平值增大,反之则表示距平值减小。据此有 (2) Mann-Kendall检验法是由世界气象组织(WMO)推荐并已广泛应用的非参数检验方法,其优点在于它能够有效地区分某一过程是自然波动还是存在确定的变化趋势。应用Mann-Kendall分别对1960年~2012年龙潭水库坝址处前、主和后汛期的洪峰流量进行突变检验,采用的计算公式如下[5]: 假设给定n个独立随机的时间序列变量(X1,X2,…Xn),构建一个秩序列 (3) 式中,Sk表示第i个样本的累计数,且有 (4) 定义统计变量 (5) 式中,E(Sk)和Var(Sk)分别是Sk的均值和方差。 给定显著性水平α,若UFK≥Uα,则表明序列存在显著变化趋势;反之,则表明时间序列较为平稳。将时间序列X按逆序排列后重复上述步骤,同时保证以下条件。即 (6) 将UBk和UFk两个统计量和给定的Uα绘制在同一张图上进行分析:若UFk的值大于0,则表明序列呈现上升趋势;反之,则呈现下降趋势。当UFk曲线超出临界线Uα时,表明序列发生了显著的变化,且超过Uα的范围为出现突变的时间区域;当UBk和UFk曲线的交点出现在临界线Uα之内,则该交点对应的时刻为突变开始的时间;如果存在多个交点或交点出现临界线以外,则需要进行进一步检验。 采用在频域和时域上局部表现性都较好的Morlet复值小波进行周期性分析,其函数式[8] ψ(t)=eicte-t2/2 (7) (8) (9) 式中,Wf(a,b)为小波变化系数;Var(a)为小波方差;a为反映小波周期长度的尺度因子;b为反映时间平移的时间因子;t为时间;f(t)为时间序列数;R为实数域。 采用滑动平均法研究洪峰流量序列(见表1)的变化趋势,结果见图1。 表1 1960年~2012年龙滩水库流域面洪峰流量数据 m3/s 图1 各分期洪峰流量变化趋势 从图1a可见,前汛期洪峰流量于1960年~1978年较为稳定,而1978年~1981年则呈现明显上升趋势, 1981年~1985年持续下降,1985年后才缓慢上升,1984年~2004年洪峰流量均低于均值。总的来说,前汛期洪峰流量整体较为稳定,以平均每年3.31 m3/s的速率缓慢递增。从图1b和图1c可以看出,主汛期和后汛期洪峰流量呈现“上升-下降-上升-下降”往复循环的波动趋势,且波动均较大;主汛期洪峰流量以平均每年5.27 m3/s的速率缓慢递增,后汛期洪峰流量以平均每年30.02 m3/s的速率递减。前、主和后汛期洪峰流量的变化趋势对比显示,后汛期洪峰流量的减小速率比前汛期和主汛期洪峰流量的增长速率要快得多。 总的来说,龙滩水库前汛期洪峰流量比较稳定,主汛期和后汛期的洪峰流量存在明显的周期性波动。此外,后汛期洪峰流量呈现较快的下降趋势,说明后汛期具有较大的蓄水潜力。即,在后汛期(9月2日~10月31日)可逐步抬高汛限水位,从而提高汛期蓄水能力,缓解地区水资源紧缺压力。 采用累计距平法分析洪峰流量阶段性变化特征,结果见图2。 图2 各分期洪峰流量累计距平曲线 从图2a可知,研究时域内前汛期洪峰流量呈现较为明显的增减交替变化规律,在此期间存在2次先急速上升后迅速下降的较大波动(1982年~1988年和2007年~2009年),且Qm在2008年达到最大,由此判断1983年和2008年可能是突变点。从图2b可知,主汛期洪峰流量于1988年出现Qm最大值;此外,在1986年、1975年和2011年等年份也出现了较大值,均有可能是突变点。从图2c可知,研究时域内后汛期洪峰流量呈现较为明显的增减交替变化规律,洪峰流量变化幅度较大,主要以大于均值的洪峰流量占优,Qm在1986年出现最值,此外,在1988年、2007年和2011年等年份都出现较大值,均有可能是突变点。 累计距平法是针对平均值计算突变的方法,不可避免受到少数特殊值的干扰。即,因序列长度不同而存在一定的差异。为了更清楚地研究洪峰流量序列的突变特性,采用Mann-Kendall检验法对前、主和后汛期洪峰流量序列分别进行突变检验。选取置信水平α=0.05,并运用Matlab软件来实现Mann-Kendall的检验步骤,计算成果见图3。 从图3a可知,UFk前汛期值在1962年~1965年和1991年~2012年这两个时段内均小于0,但没有超过临界值Uα,说明该时段内洪峰流量呈现下降趋势但趋势不明显;UFk值在1960年~1991年间均大于0且没有超过临界值,说明该时段洪峰流量呈现上升的趋势但趋势不明显。此外,UBk和UFk曲线共有3个交点且交点出现在临界线Uα之内,故这三个交点对应的时刻(1963年、1986年和2008年)为突变开始的时间。 从图3b可知,主汛期UFk值在1960年~1964年、1977年~1978年和1981年~1983年期间均小于0,但没有超过临界值Uα,说明这期间洪峰流量呈现下降趋势但不明显。UFk值在1964年~1977年、1978年~1981年和1983年~2012年期间均大于0。即,该时段洪峰流量呈现上升趋势,尤其是在1969年~1971年和2001年~2003年期间UFk值超过了临界线,说明该时段洪峰流量上升趋势明显,其他时段上升趋势不明显,1969年和2001年可能为突变开始时间。此外,UBk和UFk曲线共有2个交点,分别出现在1964年和2011年,且交点出现在临界线Uα之内;故认为1964年和2011年为突变开始的时间。 图3c显示,后汛期UFk值在1962年~1965年和2000年~2012年两个时段内均小于0,且没有超过临界值Uα,说明这两个时段内洪峰流量呈现下降趋势但不明显;在1960年~1962年和1965年~2000年这两个时段内UFk值均大于0且没有超过临界值,说明该时段洪峰流量呈现上升的趋势但趋势不明显。此外,UBk和UFk曲线共有4个交点,且交点出现在临界线Uα之内,故可认为1998年、2000年、2007年和2008年为突变开始的时间。 图3 各分期洪峰流量Mann-Kendall突变检验结果 由以上两种方法进行综合评价得到突变诊断结果见表2。 表2 突变诊断结果 分析表2可知,前汛期洪峰流量突变主要发生在20世纪,后汛期洪峰流量突变主要发生在2000年以后;前汛期和后汛期的突变点个数多于主汛期;前、主和后汛期发生突变的年份均不一样。由此说明,主汛期发生突变的可能性较小,所以在对汛限水位的动态研究中,更应注意考虑前汛期和后汛期的洪峰流量变化特征。 采用Morlet小波分析对龙滩水库坝址处1960年~2012年前、主和后汛期洪峰流量进行周期性研究,分析结果见图4。图4a、c和 图4 e是Morlet小波变换系数实部等值线图,由此可以观察洪峰流量序列在逐年时间尺度下的变化特征。为了进一步判断洪峰流量序列的周期特性,绘制小波方差图(见图4b、d和 图4 f),通过小波方差确定序列的主周期,从而揭示不同时间尺度下洪峰流量的变化情况。图4中小波系数实部的绝对值越大,说明序列变化越显著;小波系数实部为正值时,表示洪峰流量偏大,反之洪峰流量偏小。 图4 小波系数实部等值线和小波方差 从图4a可知,前汛期洪峰流量存在明显的年际变化,主要有3~6 、6~10 、10~15 a和23~28 a这4种尺度的周期变化。在3~6 a时间尺度上震荡不明显,尺度中心大致在5 a;6~10 a尺度中心在8 a,10~15 a尺度中心在13 a;23~28 a尺度下周期性震荡比较显著,其尺度中心在24 a,在1985年~1990年和2000年~2005年期间洪峰流量偏低,而在1990年~2000年和2005年~2012年期间洪峰流量偏高。 从图4c可知,主汛期洪峰流量存在明显的年际变化,主要存在3~5、5~10、10~19 a和20~28 a这4种尺度的周期变化。在3~5 a和5~10 a时间尺度上震荡不明显,尺度中心分别在4 a和7 a;10~19 a尺度下洪峰流量周期震荡比较显著,出现了“低-高-低-高”的交替震荡,其尺度中心在15 a;20~28 a也出现洪峰流量高、低交替震荡的现象,其尺度中心在24 a。 从图4e可知,后汛期洪峰流量存在明显的年际变化,主要存在3~5、8~12 a和15~25 a这3种尺度的周期变化。在3~5 a时间尺度上震荡不明显,尺度中心大致在4 a;8~12 a尺度出现洪峰流量高、低交替震荡的现象,其尺度中心在11 a;15~25 a尺度下洪峰流量周期震荡比较显著,其尺度中心在18 a,在该尺度下出现较多的高、低交替震荡,其中1960年~1964年和1973年~1977年期间洪峰流量偏小。 从图4b可以看出,前汛期洪峰流量小波方差对应的峰值是24 a,即在该尺度下波动最强,为第一主周期,其次,13、8 a和6 a分别为第二、第三和第四主周期;从图4 d可以看出,主汛期洪峰流量小波方差对应的峰值是15 a,即在该尺度下波动最强,为第一主周期,其次,24、4 a和7 a分别为第二、第三和第四主周期;从图4 f可以看出,后汛期洪峰流量小波方差对应的峰值是18 a,即在该尺度下波动最强,为第一主周期,其次,11 a和4 a分别为第二和第三主周期。 综上所述,可以得出以下结论:①前、主和后汛期洪峰流量的变化周期存在差异,在制订汛期分期调度方案时,应该注意这种周期性变化差异;②前、主和后汛期洪峰流量均存在各自变化周期,说明在研究洪水的周期性时,更应注意洪水的年际周期变化。 (1)由趋势性分析可知:前汛期和主汛期洪峰流量均呈现缓慢上升的趋势,而后汛期洪峰流量呈现快速下降趋势,说明该流域可以在后汛期(9月2日~10月31日)多蓄水,从而达到利用洪水资源缓解水资源紧缺压力的目的。 (2)由突变性分析可知:前汛期和后汛期的洪峰流量突变次数多于主汛期洪峰流量突变次数,由此认为今后前汛期和后汛期洪峰流量发生突变的可能性较大。建议在当前全球气候变化背景下,制定调度计划时更应该注意分期洪水的年际突变特性。 (3)由周期性分析可知:前、主和后汛期洪峰流量的变化周期分别为24、15 a和18 a。分期洪水的周期性存在差异进一步说明,只有通过对汛期分期,才能合理、详细地描述洪水变化规律,从而才能制定合适的防洪调度方案。 [1] 国家防汛抗旱总指挥部, 中华人民共和国水利部. 2016年中国水旱灾害公报[M]. 北京: 中国地图出版社, 2017. [2] 陈磊, 王义民, 畅建霞, 等. 黄河流域季节降水变化特征分析[J]. 人民黄河, 2016 (9): 8- 12, 16. [3] 刘增进, 李东琴, 张海涛, 等. 霞曲流域1956~2010年降水趋势分析[J]. 华北水利水电大学学报: 自然科学版, 2015 (4): 12- 14, 19. [4] 张应华, 宋献方. 水文气象序列趋势分析与变异诊断的方法及其对比[J]. 干旱区地理, 2015 (4): 652- 665. [5] 普发贵. Mann-Kendall检验法在抚仙湖水质趋势分析中的应用[J]. 环境科学导刊, 2014, 33(6): 83- 87. [6] 刘俐. 基于变点—模糊理论的龙滩水库汛期分期调度研究[D]. 南宁: 广西大学, 2015. [7] 王文圣, 丁晶, 金菊良. 随机水文学[M]. 北京: 中国水利水电出版社, 2008. [8] 王文圣, 丁晶, 李跃清. 水文小波分析[M]. 北京: 化学工业出版社, 2005.2.2 累计距平法

2.3 Mann-Kendall检验法
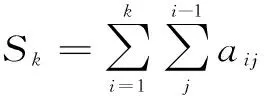

2.4 小波分析

3 分析结果
3.1 趋势性分析

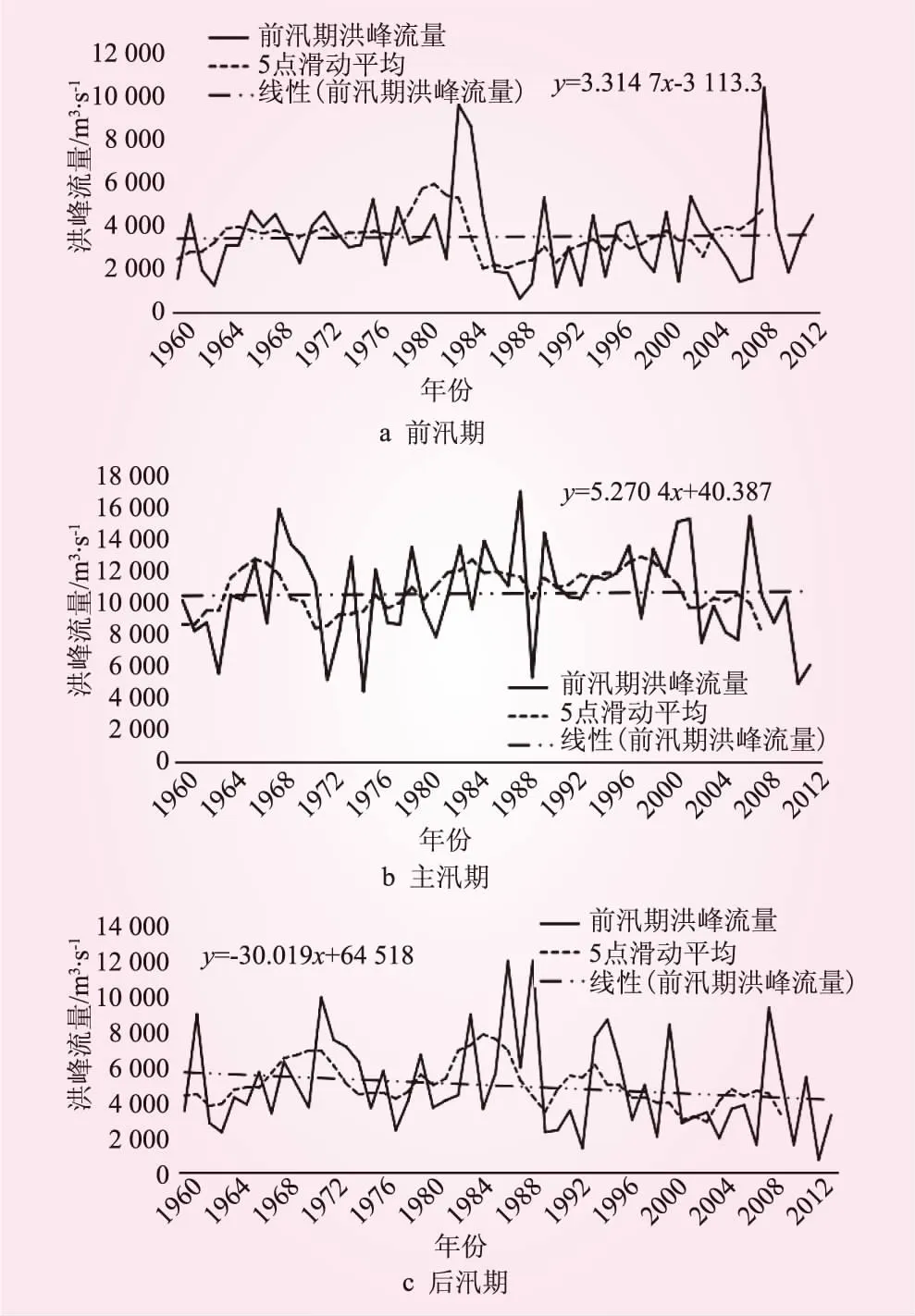
3.2 突变性分析
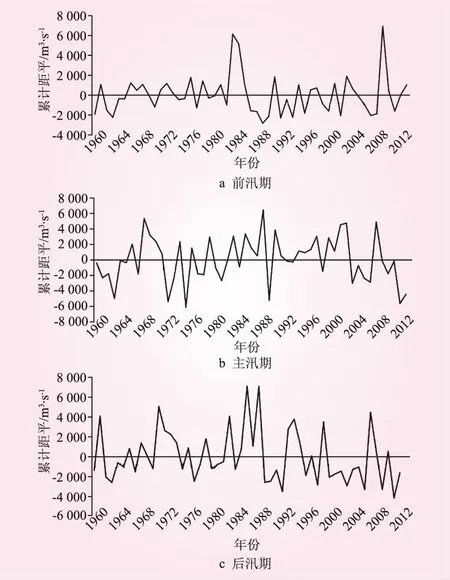


3.3 周期性分析

4 结 论
