基于过渡理论的不同论域对汛期分期影响研究

王权威，祝雪萍，武鹏林，唐 莉

(太原理工大学水利科学与工程学院，山西太原030024)

0 引 言

实际工作中，分期设计洪水与分期调整汛限水位的基础是合理的确定汛期分期，汛期分期对于流域、水库防洪及洪水的安全利用等具有重大意义[1]。汛期因其具有随机性、确定性、模糊性等变化规律[2]，其汛期分期的方法也多种多样，现行汛期分期方法主要有[3-5]：数理统计法、Fisher最优分割法、模糊集分析法、变点分析法、分形分析法等。这些方法存在或选取指标单一或计算繁琐等缺陷，都不能提供简便合理的汛期分期途径[6]。汛期分期是一个稳定—过渡循环交替的状态，非汛期稳定一个时间段过渡到汛期，汛期稳定一个时间段再过渡到非汛期，以及前汛期稳定一个时间段过渡到主汛期再到后汛期，汛期的变化过程符合过渡状态的理论基础。

本文以过渡理论为基础，提出了数学概念清晰、理论功能强大的稳定-过渡判别模式，结合主成分分析法对张家庄水库进行不同论域的汛期分期，并进行对比分析。

1 理论基础

1.1 过渡理论

过渡状态研究事物的渐变过程，具有模糊性、混沌性以及分形性等特点。

若用过渡集合表示在论域U上的任一过渡状态，其中Ui与Uj分别表示了过渡态Uij所对应的两个稳态，且有U=Ui∪Uj∪Uij与Ui∩Uj∩Uij=Ø成立[7]。

为了能够获得过渡集合U中任一元素u在从Ui到Uj的过渡过程中所具有的过渡特征刻画，给定过渡映射T:U→[0，1]

u→τ(u)

则τ(u)为从稳态Ui到Uj的过渡率，具体写为

(1)

其分别对应了元素u处于完全未过渡、过渡过程中、与完全已过渡等三种过渡阶段的过渡率映射结果，其过渡集合的类文氏图如图1所示。

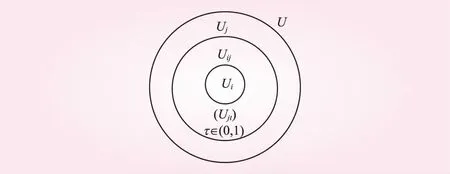
图1 过度集合的直观解释

1.2 均值变点

汛期的开始时间是雨量由少到多的时刻，会存在变点；而汛期的结束时刻是雨量由多到少的时刻，也会存在变点[8]。相似地可以得到：主汛期的开始时间是降雨强度由低到高的过渡，在这个时刻会存在“变点”；而主汛期的结束时刻则是降雨强度由高过渡到低的时刻，同样在这一时刻也会存在“变点”。由过渡理论可以看出，过渡率和降雨指标变化之间具有正相关的关系。故，可以从寻找降雨强度的变点转化为寻找过渡率的变点。本次采用均值变点分析法来寻找变点，然后根据变点进行分期，均值变点分析的步骤如下：

对于有序旬过渡率数列{xθ}(θ=f，f+1，…，d；f与d分别代表汛期开始和结束的旬)，因为汛期或者主汛期的开始时刻与结束时刻分别在临界过渡率所对应的旬的前面和后面，所以按照数列中的临界过渡率，把有序旬过渡率数列划分为两列即：xf，xf+1，…，xt和xt，xt+1，…，xd，其中xt=max(xf，xf+1，…，xd)或xt=min(xf，xf+1，…，xd)。

假定有序旬过渡率数列xf，xf+1，…，xt或xt，xt+1，…，xd，在第θ个旬与第θ+1个旬处断开，则可计算统计量Dt和D，见式(1)、(2)

(1)

(2)

β=D-Dt

(3)

则最大β对应的第θ个旬即为变点，从而可以求出主汛期开始的旬。

同理，对有序数列xt，xt+1，…，xd进行上述演算，也就可以得到主汛期结束的旬。根据主汛期开始与结束的旬，可以对汛期进行汛期分期。

2 稳定-过渡判别模式原理与步骤

正如模糊集可以由隶属函数所刻画那样，汛期过渡集合也可以由临界过渡率所刻画；而临界过渡率的大小又依赖于临界过渡函数的形式，对应于不同的临界过渡函数可以得到不同的汛期过渡集合特征刻画。根据临界汛期过渡态自身所具有的模糊性与随机性，临界过渡函数的选取需将两者相结合。过渡率函数为

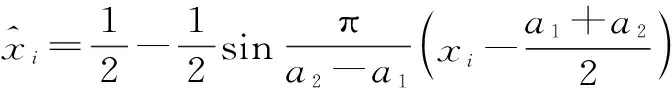
(4)

式中，a1=minxi，a2=maxxi。

水库每年从非汛期过渡到汛期，又从汛期过渡到非汛期，并且在汛期内，又可以从前汛期过渡到主汛期再到后汛期，可将汛期划分视为连续的多个过渡状态，以往对于汛期人为的定为6月～9月或者6月～11月等，运用过渡理论，可同时进行汛期划分与汛期分期，克服传统的人为界定汛期的主观性。具体步骤如下：

(1)构建n个指标特征值矩阵

其中，xit为时序t指标i特征值，共有n个指标。

(2)根据式(4)确定各个指标在时序t内的过渡率。 确定时序研究对象指标i的特征值xit落入非汛期与汛期或汛期与非汛期的过渡率为1和0的标准值区间矩阵Ni1，Ni2，已知矩阵X，可得标准区间矩阵Y=(Nih)，其中i=1，2，3…n;h=1，2；则

Ni1=(minxit，maxxit)，Ni2=(maxxit，minxit)

(5)

其中，maxxit，minxit分别为时序集xit的最大、最小特征值，即maxxit=a2，minxit=a1。

(3)确定各指标的权重wi。

(4)计算xit综合过渡率

(6)

式中，α为优化准则参数；P为距离参数。α=1为最小一乘方优化准则，α=2为最小二乘方优化；考虑到α=2对距离具有放大或缩小效应，因此，在汛期分期的应用中，选取α=1。若采用优化准则参数α=1，距离参数为海明距离，即P=1，则式(6)变为线性公式

(7)

若为非线性系统，可采用欧氏距离，即P=2，式(6)变为

(8)

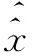
3 实例应用

3.1 流域概况

张家庄水库位于孝义市旧城西2.5 km的孝河上，属于暖湿带大陆性季风气候，多年平均径流量468 mm左右，控制流域面积465.1 km2。张家庄水库是孝河流域干流上主要的蓄水防洪工程，具有防洪、工业、灌溉、生态旅游、供水的综合功能。

3.2 研究期确定

以降雨补给径流为主的流域，其降雨量与径流量间存在相关性。枯水期降雨量少，相关系数较低；而丰水期时降雨补给径流充沛，相关系数很高[9]。这样就可形成年际内降雨与径流的相关系数序列，可利用月径流-降雨相关系数序列，采用基于过渡理论的稳定-过渡判别模式，定量的确定汛期分期的研究域。

本文统计分析了张家庄水库1994年～2014年共21年的月降雨-径流资料，得到了降雨P和径流R的平均相关系数矩阵X=[0.02 0.24 0.22 0.39 0.64 0.72 0.73 0.67 0.75 0.50 0.29 0.01]。

再据X可得从非汛期过渡到汛期再从汛期过渡到非汛期的相关系数两个标准区间矩阵：Y11=[0.02 0.75]；Y12=[0.75 0.01]。

根据稳定-过渡判别模式原理与步骤得到降雨P和径流R的相关系数过渡矩阵：X′=[1.00 0.79 0.83 0.49 0.06 0 0 0 0 0.26 0.70 1.00]。

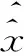
3.3 基于旬的汛期分期

在分期汛限水位调度模式下，需要根据洪水暴雨特征进一步的对汛期分期。由上述分析可得6月～9月为汛期分期的研究域。在6月～9月中，本文首先以旬为单位，将整个研究域划分为12个旬。依据张家庄水库1962年～2014年的共53 a的逐日降雨资料，选取能反映张家庄水库流域范围内暴雨洪水特征的四个指标：多年平均旬降雨量，多年平均旬最大一日雨量，多年平均旬最大三日雨量，暴雨天数(日降雨量>25 mm)。每一旬各指标的取值利用逐日降雨资料统计得到，标准化后得

据矩阵X1可得从汛前期过渡到主汛期和从主汛期过渡到后汛期指标的两个标准区间矩阵分别为：

运用用SPSS软件对标准化的样本数据进行主成分分析，可得表1及表2。

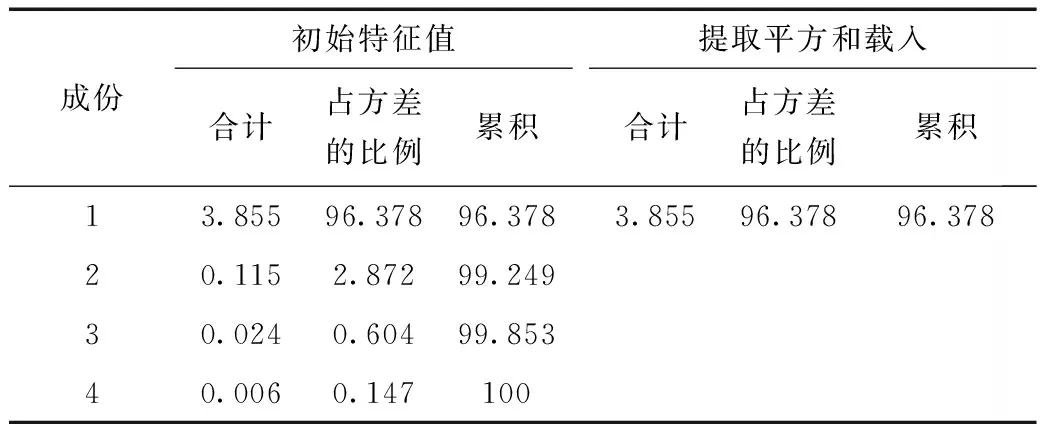
表1 解释的总方差 %

由表1可知，主成分1特征累积方差贡献率≥90%。因此，第一个主成分能够反映各指标的大部分信息。

表2 成分矩阵

综合得分模型为：F=0.486X1+0.084X2+0.038X3+0.019X4。

各指标的权重为：ω=(ω1，ω2，ω3，ω4)=(0.776，0.133，0.061，0.09)。

应用式(4)与矩阵Y11和Y12，可得从汛前期过渡到主汛期和从主汛期过渡到后汛期各降雨指标的过渡率矩阵

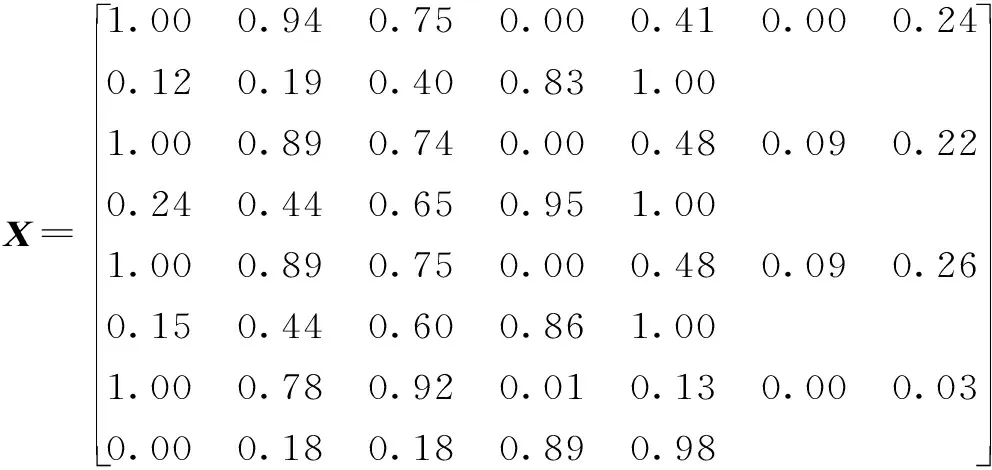
采用主成分分析法所得权重，根据式(6)可得到在线性模型和非线性模型下的相对过渡率。

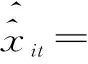
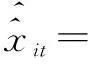
0.00 0.38 0.02 0.22 0.12 0.21 0.40 0.83

1.00]。

按照数列中的临界过渡率，把有序旬过渡率数列划分为两列即：1.00，0.91，0.73，0.00和0.00，0.38，0.02，0.22，0.12，0.21，0.40，0.83，1.00。

分别使用式(1)、(2)、(3)计算β。β在设定不同的断开情况下的变化见图2。

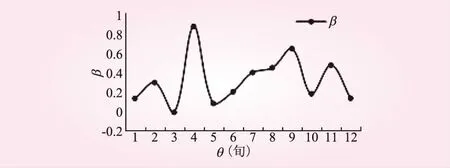
图2 β随 θ变化

由图2可知，将有序旬过渡率数列划分为两列时，β取到最大值对应的点分别为第4个旬与第9个旬，则第4个旬与第9个旬为变点。即：前汛期为6月1日至6月30日，主汛期为7月1日至8月20日，后汛期为8月21日至9月30日。

3.4 基于候的汛期分期

在6月～9月的研究论域中，以候(5 d)为基本单位，将整个研究论域划分为24个候。仍选取上述4个指标构造样本阵，并对数据标准化。

由主成分分析法得到各指标的权重为：ω=(ω1，ω2，ω3，ω4)=(0.76，0.15，0.07，0.01)。

采用主成分分析法所得权重，根据式(6)可得到在线性模型和非线性模型下的相对过渡率。

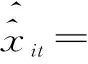
0.95 0.95 0.56 0.08 0.35 0.67 0.55 0.71 0.00 0.07 0.99 0.16 0.92 0.86 0.33 0.89 0.90 1.00 0.96 1.00 0.92]。

按照数列中的临界过渡率，把有序旬过渡率数列划分为两列即：0.99，1.00，0.91，0.95，0.95，0.56，0.08，0.35，0.67，0.55，0.00和0.00，0.07，0.99，0.16，0.92，0.86，0.33，0.89，0.90，1.00，0.96，1.00，0.92。

表3 基于不同论域的汛期分析结果

分别使用式(1)、(2)、(3)计算β，图3所示为β在设定不同的断开情况下的变化图。

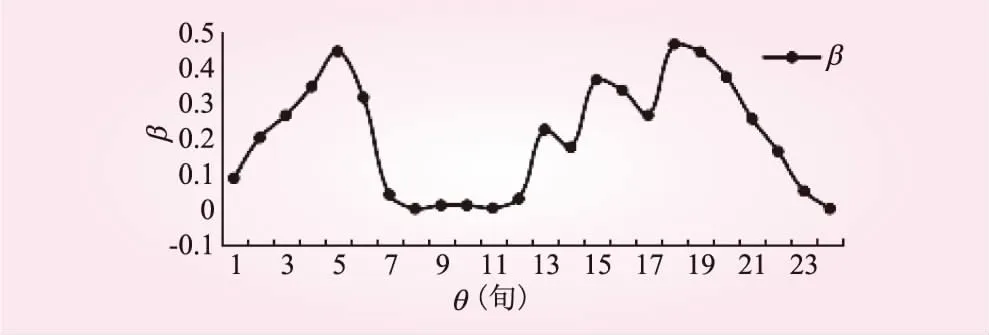
图3 β随 θ变化

由图3可知，对于前半部分变点为第5个候为变点，对于后半部分变点为第18个候为变点，即前汛期为6月1日至6月20日，主汛期为6月21日至8月25日，后汛期为8月26日至9月30日。

3.5 结果比较与分析

表3给出基于候和旬对张家庄水库汛期分期结果比较。从表3可以看出，本研究得到基于候的汛期分期得到的主汛期更长，有益于水库控制流域内主要河流重点河段、重要城镇的防洪安全。基于旬的汛期分期与Fisher表现出较高的一致性，但汛期划分与Fisher存在一定差别。从成因上看，孝河流域呈显著的大陆性季风气候，冬季蒙古高压鼎盛，该流域接近高压中心，降雨较少；3月～5月份季风开始转变，气团活动开始频繁，但是风沙很大，降雨也相对不多；从6月～9月开始，受东南季风支配，并在山西和河南之间发育的一个小低压与副热带海洋气团接触，再加之有因对流和地形抬升形成大量的降雨，且大暴雨多发生在7月中旬到8月初。9月开始，气温开始降低，地面气压场开始转变，该流域开始受槽后西北气流控制，降雨开始减少。由判别模式法得到汛期为6月～9月，相比Fisher最优分割的5月～10月与降雨天气系统更为一致的，符合洪水季节规律和成因特点，本文的分析方法更为合理的。

4 结 论

(1)分期论域对分期结果有一定影响，在实际中应细化汛期分期论域，让分期结果更精确；同时，也可对不同的防洪安全标准制定不同的汛期分期论域。另外，也可以利用不同论域的分期结果，提供防洪安全或挖掘洪水资源潜力的依据。

(2)本文提出的方法分期结果与降雨天气系统更为一致，符合洪水季节规律和成因特点，有较强的理论背景，数学概念清楚。

(3)本文提出的方法计算方便，结果直观，汛期划分以及汛期分期更合理。

[1] PENG Yang, JI Changming, LIU Fang. Impounding time and objective decision of Siluodu-Xiangjiaba cascade reservoirs in the flood recession period[J]. Journal of Basic Science and Engineering, 2014, 22(6): 1098- 1107．

[2] LI Min, CHEN Shouyu, WANG Yuntao, et al. Multi-criteria recognition method for flood seasonality based on variable sets[J]. Journal of Hydraulic Engineering, 2013, 44(12): 1420- 1424．

[3] 蒋海艳, 莫崇勋, 韦逗逗, 等. 水库汛期分期研究综述[J]. 水利水电科技进展, 2012 (3)： 75- 80．

[4] 高波, 刘克琳, 王银堂, 等. 系统聚类法在水库汛期分期中的应用[J]. 水利水电技术, 2005 (6)： 1- 5．

[5] 刘攀, 郭生练, 王才君, 等. 三峡水库汛期分期的变点分析方法研究[J]. 水文, 2005 (1)： 18- 23．

[6] 肖聪, 顾圣平, 崔巍, 等. Fisher最优分割法在李仙江流域汛期分期中的应用[J]. 水电能源科学, 2014 (3)： 70- 74．

[7] 陈洪亮. 过渡状态可视化理论、 方法及其应用研究[D]. 杭州： 浙江大学, 2002．

[8] WANG Hejia, XIAO Weihua, WANG Jianhua et al. The impact of climate change on the duration and division of flood season in the Fenhe River Basin[J]. Water, 2016(8)： 1- 11．

[9] 唐莉, 张永波, 祝雪萍, 等. 基于PCA-Fisher最优分割法的汛期分期影响研究[J]. 水力发电, 2018, 44(1)： 13- 16, 76．