找准起点坐标，促进概念形成<br/>——以“倍的认识”的教学为例

找准起点坐标，促进概念形成
——以“倍的认识”的教学为例

2018-06-22浙江平湖市叔同实验小学314200

小学教学参考 2018年17期

浙江平湖市叔同实验小学（314200）

高斯曾经说过：“在数学中重要的不是符号，而是概念。”概念不仅是数学基础知识的重要组成部分，更是学生理解、分析和解决问题的前提。概念学习分为两种方式：概念形成与概念同化。所谓概念形成，是指从大量情境或实例出发，分析、类比、归纳，概括出概念的本质特征，从而形成新概念。尽管关注概念形成已成为共识，然而在具体的教学过程中仍然存在着许多不足。下面将以“倍的认识”一课的教学为例，通过分析教学现状，给出相应的教学策略。

一、现状

对于“倍的认识”这一课，“概念同化”是最常见的教学方式：首先借助主题图与实物，展现圈一圈、摆一摆、画一画等图示表征方式；然后师生共同概括出“倍”的概念；最后通过一系列变式，让学生在观察和操作中体会“一倍量”变化所引起的倍数变化，以及“‘一倍量’不变，倍数变化，比较的结果也在变化”。

然而，对于问题“□□□□□□，□的个数是○的3倍，○画几个？”有将近70%的学生认为是6×3=18（个），只有不到15%的学生能准确画出2个○，并清楚地说出自己的想法。由此可见，这样的概念教学方式存在着一些问题。

1.学习起点把握不准确，知识沟通不顺畅

“倍的认识”是在学生学习了一、二年级的“比多少”和三年级的乘法知识之后教学的，“倍的认识”这一课是从两个量的绝对数量的比较，向两个量相对数量的比较之间的过渡，也是学习分数、百分数、比和函数等概念的基础。其实对于学生而言，这两种比较存在着共同点——都是通过一个量去说明另一个量，而“倍”更多的是关注多倍量中有几个“一倍量”。然而，教师往往容易忽视学生对于比较两个量的认识起点，轻视了“倍”与“比多少”“份”之间的联系。这样就导致新旧知识之间沟通不良，学生学习新概念如空中楼阁，没有扎实的地基。

2.教学活动重同化过程，轻形成过程

对于“倍的认识”这一课的概念教学，很多教师采用概念同化的教学方式，以定义的方式呈现“倍”这一概念的本质特征，替代学生对概念本质属性的揭示，以演绎的思维方式引导学生接受、理解概念，并将概念纳入自身的概念体系中。这种“短平快”的概念教学方式，偏重讲授概念的逻辑结构，忽视了知识的形成过程，导致学生对概念形成缺乏参与体验，造成部分学生对于“倍”以谁为“标准”，以及“一倍量”“多倍量”的变化情况理解不到位。

3.练习层次不丰富，思维提升不显著

在教学完“倍的认识”后，教师多采用各种变式练习来帮助学生巩固“倍”的知识，往往缺少开放性问题，缺乏展现不同学生思维能力的平台，从而造成学生在理解“倍”的本质时比较片面。

二、不同想法

1.以学情为导索，找准知识起点

教师在教学任何内容之前，都需要明确学生的已有生活经验、认知水平和情感诉求，即学生的兴趣点与困难所在，以学情为前提，找准知识的起点，也就是“以学生的活动为基点”来设计和展开教学，着重考虑学生需要学什么，怎样学才能学得好。

（1）找准联结点，情境导入

数学概念不是独立存在的，它们在本质上都是有联系的，因为数学中的任何一个概念，只有与其他概念相联系，才能生成和发展。引导学生明确这些概念之间的联系，找准新旧知识的联结点，以学生的认知诉求为前提，并结合一定的教学情境，才能帮助学生更好地理解概念。

【教学片段1】

师（出示图1）：你从图中发现了什么？

生：多2个；多2倍；3倍。

图1

图2

师（出示图2）：你又有什么发现？

师：图1和图2有什么相同点？

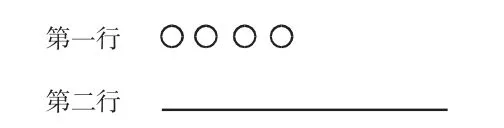
图3

师：仔细观察图1和图2，根据图1和图2的规律，图3的横线上应该画几个○？

生1：图3的横线上要画○○○○○○○○○○○○。

师：为什么画12个？

生1：图1把一个看作1份，第二行有3份；图2把2个看作1份，第二行有3份；图3把4个看作1份，第二行也要画3份。

对于两个量之间的比较，既可以比较它们的绝对关系，比如“比多少”，还可以比较它们的相对关系，比如“倍”与“几分之几”。然而对于大部分三年级学生而言，“比多少”与“找规则”是已有经验，“倍”是第一次接触。通过比较图1和图2的相同点这一问题情境，学生找到新概念与已有知识之间的联结点，既激发了学习兴趣，又能从“倍”的角度思考问题，在教师的适时适度引导下“提领而顿，百毛皆顺”。

（2）聚焦冲突点，建立模型

小学阶段的概念学习往往是新的需要与学生原有的数学水平之间存在着认知冲突，而正是这种冲突就能引发学生的思考，让学生产生新的学习内驱力。教师需要准确把握知识的冲突点，并以此为切入口，以清晰的图形表征建立模型，帮助学生形成对倍的初步认识。

【教学片段2】

师（出示图4）：你们能看懂图4吗？

图4

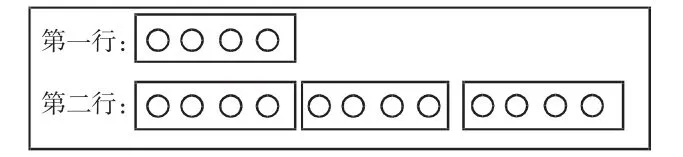
图5

师（出示图5）：有同学是用框一框的方法，这是什么意思？能不能也这样画12个，并框一框呢？

师：我们把第一行的4个看成1份，第二行有这样的3份，就是几个几？（3个4）可以说第二行○的个数是第一行的多少？

师：虽然图1、2、3中的○数量都不一样，但是第二行○的个数都是第一行的——3倍，如果现在要把第二行○的个数变成第一行的4倍，要增加几个○呢？

师：现在都是4倍了，为什么有些地方增加了1个，有些地方增加了2个，而这里要增加4个呢？

“为什么画12个？”这是本课的一个冲突点，借助“份”来帮助学生理解“倍”，通过研究一份和多份之间的关系，沟通“倍”与原有知识“份”之间的联系，让学生自发地想到两个量之间还可以用“倍”来表示，促使学生理解“倍”的共同属性。变式练习中“如果把第二行○的个数变成第一行的4倍，为什么每幅图增加的个数不一样？”这是第二个冲突点，通过画一画使学生理解因为“一倍量”不同，因此每次增加的个数也不同，使学生第一次感受到“一倍量”的重要性，从而为丰富“倍”的内涵服务。

2.以内容为抓手，完善形成过程

富兰克林曾说：“告诉我的，我会忘记；展示给我的，我会记住；我参与其中的，我会理解与运用。”当课堂进入交流与合作探究的阶段，如何让不同层次的学生都能在共同参与的过程中形成“倍”的概念，理解其本质内涵，这离不开教师对教学内容的重新解读与再设计，缺少不了对比辨析与强化练习。

（1）从文到形，对比显本内涵

知识网络的构建往往要经历一个“建立—分解—重建”的过程，概念学习也是如此。学生经历了概念的发生与形成后，更需要一个分解重建的过程，从而在对比练习中完善“倍”的模型。

【教学片段3】

图6

图7

师：红萝卜比白萝卜多3根，对应的是图6还是图7？

师：红萝卜的根数是白萝卜的4倍，对应的是图6还是图7？

师：对于图6和图7中的小A和小B，你觉得谁说的话更有水平？为什么？

生1：小B,因为他的一句话包括两幅图的内容。

师：红萝卜的根数是白萝卜的4倍，可以表示红萝卜有4根，白萝卜有1根；红萝卜有8根，白萝卜有多少根？还可以表示红萝卜有几根，白萝卜有几根？

师：这样的例子举得完吗？只要符合怎样的条件，红萝卜就是白萝卜的4倍呢？

通过第一个问题“红萝卜比白萝卜多3根”，找到匹配的是图6，帮助学生回顾“比多少”的知识；对于第二个问题“红萝卜的根数是白萝卜的4倍，对应的是图6还是图7”，学生的第一反应是选择图6，因为当“一倍量”为1个时，“多倍量”就是4个，在图6上就能清晰地看到。也有学生发现还可以把2个白萝卜看成1份，红萝卜就有4个2，因此也可以说红萝卜的根数是白萝卜的4倍，这样，一句话对应两幅图，打通了文字与图形的壁垒。第三个问题“谁说的话更有水平”，学生明显感到小B可以用一句话概括两幅图的意思，其实就突出了4倍的本质意义。最有价值的是最后一个问题“只要符合怎样的条件，红萝卜就是白萝卜的4倍呢？”，再次凸显“倍”的本质属性。

（2）由形到文，概括正核心

对“倍”的了解需要经历一个继续探究的过程，学生只有探究大量具体的实例后，才能逐步建立“倍”的概念。通过精练的语言描述能帮助学生重新审视“倍”的含义。

【教学片段4】

师（出示图8和图9）：我们刚才认识了新朋友——倍，接下来继续用“倍”的眼光去解决一些问题。