Liu-cos混沌系统在声波弱信号检测中的应用

刘剑鸣, 习敬伟(燕山大学 电气工程学院， 河北 秦皇岛 066004)

1 引 言

混沌系统对输入信号敏感、抗干扰性好，是弱信号检测领域的一个新研究方向。2000年，聂春燕等人分析了二维Duffing混沌系统的弱信号检测性能[1]；2006年，衣文索等人提出二维Duffing振子与弱正弦信号参量估计[2]；2013年，刘海波等人提出了对Duffing混沌系统的逆向相变检测法[3]；2016年，时培明等人提出双耦合Duffing混沌振子微弱信号检测方法[4]。

通过多年改进，传统Duffing混沌系统在弱信号检测性能方面得到了很大提升，但仍有两个问题一直没有解决：(1) Duffing混沌系统变量x和y输出为周期态和混沌态，在检测时很难区分；(2) Duffing混沌系统只能窄域信号检测。当检测信号增强时，Duffing系统输出由混沌态进入周期态，继续增强检测信号，系统输出又回到混沌态，给信号检测造成混乱。

其后，三维Liu混沌系统被发现[5～7]；2005年，Choe等人通过抑制方法使三维Lorenz混沌系统中的一个变量收敛于零[8],但是带来了稳定性变差；2013年，孟玲玲等人提出了混沌和类周期态两种状态的Lorenz混沌检测系统[9]。上述研究成果仍然没有解决混沌系统窄域检测和收敛性的问题。

2016年，本课题组提出了多个三维混沌弱信号检测系统[10]，并发现Liu-cos混沌系统效果相对最好[11]。

2 传统Duffing混沌系统性能

Duffing混沌系统方程式为：

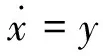
(1)

取k=5，当r超过阈值继续增大后，系统交替出现混沌态和周期态，临界值不唯一，检测范围具有窄域性。两种状态波形幅值、频率接近，难以区分。系统李雅普诺夫指数仿真如图1。

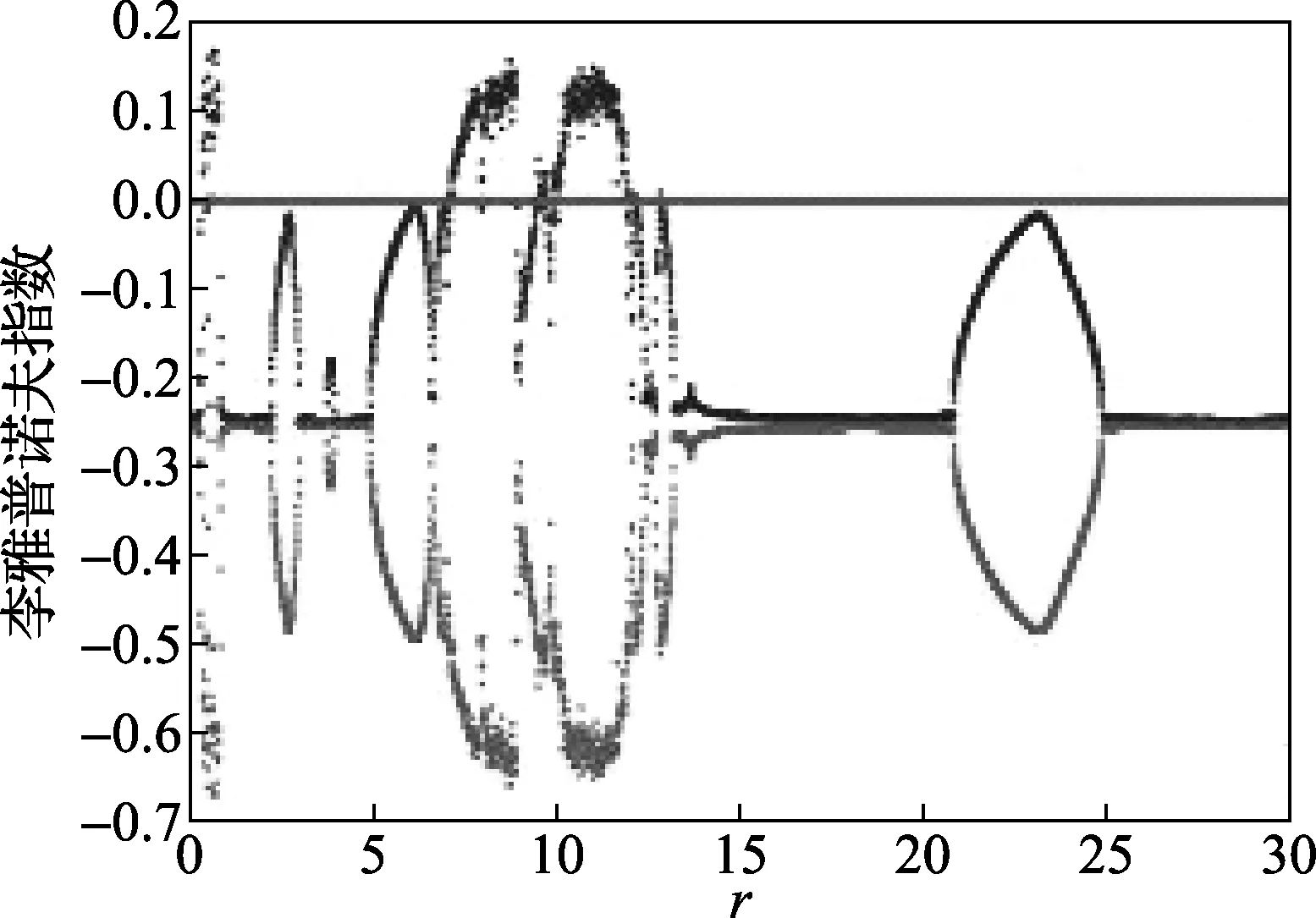
图1 Duffing系统李雅普诺夫指数图

3 Liu-cos混沌系统性能

3.1 系统动力学特征

三维Liu-cos混沌系统方程式为：

(2)

取a=2.4，b=2.5，c=7，ω=1，r=1.8，系统特征如图2和图3。

图2 相平面图

图3 时序图

仿真实验显示Liu-cos系统相平面有界非重叠、时序无序、系统具有混沌特征。

3.2 傅里叶-李雅普诺夫广域收敛判别算法

将rcos(ωt)用X替代，由式(2)得：

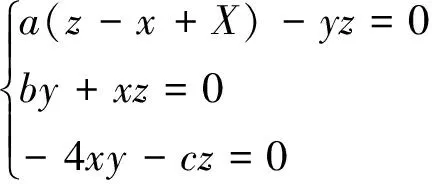
(3)

特征方程：

(a+λ)(λ2-(b-c)λ-bc+4X2)=0

(4)

ejω0t=2 p δ(ω-ω0)

(5)

cos(ω0t)=(e-jω0t+ejω0t)/2

= p δ(ω-ω0)+ p δ(ω+ω0)

(6)

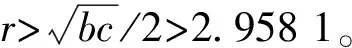
令ω=1，v=ωt，得Liu-cos系统方程式：

(7)

对常数σi(i=1,2,…,n)，设：

(8)

设U和Q为n阶和n×1阶常数阵，系统存在映射xk+1=f(xk)，在平衡点xp=(rcosωt,0,0)处的雅克比阵为J(xp)，构造uk(k=1,2,…,n)输入序列满足：

uk=Uxk+Q

(9)

(10)

将输入序列uk加入系统映射右面得：

xk+1=f(xk)+uk

(11)

经过整理计算得：

xk+1=f(xk)-f(xP)+J(xP)(xP-xk)+

E(xk-xP)+xP

(12)

式(12)显示在输入序列作用下，系统在点xp周边存在吸引域，域内点将收敛到平衡点，平衡点雅克比阵J(xp)=E，平衡点xp即为系统稳定点，对角阵E中σi既为系统李雅普诺夫指数，当σi全部为负实常数时，系统在点xp处特征值λi=eσi，此时系统收敛，在广域平衡点(rcosωt,0,0)处变量x平衡于输入驱动信号，变量y和z收敛到0。

3.3 Liu-cos系统仿真分析

(1)广域检测

取a=2.4，b=2.5，c=7，ω=1，广域李雅普诺夫指数仿真实验结果如图4所示。

图4 李雅普诺夫指数图

(2)收敛性

在系统临界状态，加入0.000 001待测信号，系统仿真输出如图5所示，显示系统变量y和z收敛到0。

图5 各变量输出时序

仿真实验显示Liu-cos混沌系统临界值唯一，检测范围具有广域性，变量y和z输出混沌和收敛态区分明显。

4 Liu-cos混沌系统声波检测

4.1 检测系统的构成

声波检测系统包括：声波发射器、声波接收器、Duffing和Liu-cos混沌电路板、示波器,如图6所示。

图6 检测系统实物图

(1)声波发射器：选用数字音频编辑器软件GoldWave对音频信号进行编辑、播放，通过连接电脑的粉色喇叭间歇发射500 Hz正弦声波信号。

(2)声波接收器：选普通话筒进行音频放大，将声音信号转化为微弱电信号，经两级电压放大和一级功率放大为1.6 V电信号后输入混沌电路板。

(3)Duffing和Liu-cos混沌电路板：用电路仿真软件Multisim设计混沌电路板，然后利用运算放大器ADTL084A和乘法器AD633(x和y输出最大非线性度分别为4 mV和1 mV)制作混沌电路板。

(4)最后用示波器观察混沌电路板接收声波信号后的输出波形变化。

4.2 与Duffing电路收敛性对比

声波发射器间歇发射500 Hz正弦声波信号，声波接收器将声音信号转化为极其微弱电信号，经三级放大后输入Liu-cos电路板，变量x、y、z输出时序如图7所示。图7中，上面波形为x输出，中间为y输出，下面为z输出，最下面为500 Hz输入信号。

图7 Liu-cos混沌电路输出时序

扬声器间歇发射500 Hz正弦声波信号，通过声波接收器转换放大后输入Duffing混沌电路板，变量x和y的输出时序如图8所示。

图8 Duffing混沌电路输出时序

通过比较可见，Duffing混沌电路板的输出混沌和大周期区分不明显。Liu-cos混沌电路板变量y和z输出由混沌变为收敛区分明显，过渡过程短暂，电路反映灵敏，便于接下电路辨识处理。

4.3 广域检测

逐渐放大输入信号到10 V，Liu-cos混沌电路板变量x、y、z的输出时序如图9所示。

图9 Liu-cos混沌电路加强信号的输出

变量y和z输出一直保持收敛状态。显示Liu-cos混沌电路可进行cos信号幅值广域检测。

4.4 与Duffing电路检测信号频率对比

取Liu-cos混沌电路板基准频率500 Hz，测量到500.2 Hz频率声波信号时，变量y和z间歇混沌输出波形如图10。利用间歇时间间隔计算外部被测信号频率是Liu-cos混沌电路另一个应用场合。

图10 Liu-cos电路输入500.2 Hz信号的输出

取Duffing电路板基准频率500 Hz，测量到500.2 Hz频率声波信号时，输出波形如图11。

图11 Duffing电路输入500.2 Hz信号的输出

图10和图11显示Liu-cos混沌电路板变量y和z输出间歇混沌和收敛信号变化明显，易于计算被测量声波信号频率。Duffing混沌电路间歇混沌和大周期信号的幅值、频率过渡过程缓慢，不利于区分和计算。

5 抗窄带噪声干扰

宽带信号与窄带信号目前的定义不尽相同，计算窄带信号与宽带噪声相比的信噪比意义不大，最好是换算到谱级比较。Liu-cos混沌系统的谱级信噪比经过计算得：

(13)

式中：sum表示求和运算；abs表示开平方运算；x(f)为待测信号功率；n(f)为噪声信号功率。

5.1 火车持续低频声波干扰

在火车低频噪声干扰下，Liu-cos混沌电路板输出如图12。上部为变量x、y和z输出，底部信号为火车低频干扰声音和500 Hz声波信号相混合放大后输入混沌电路的波形，实际实验显示500 Hz输入信号在低频噪声干扰下波形已完全变形，但对变量y和z输出波形收敛性能影响轻微，说明Liu-cos电路具有很好的抗低频、窄带噪声干扰的能力。

图12 火车声波干扰时的输出时序

5.2 突加闷雷低频声波干扰

Liu-cos混沌电路在闷雷低频声波干扰下的输出如图13。图中底部信号前部为500 Hz声波信号输入，1/3处为加入低频闷雷噪声和500 Hz声波信号混合放大后输入混沌电路的波形。

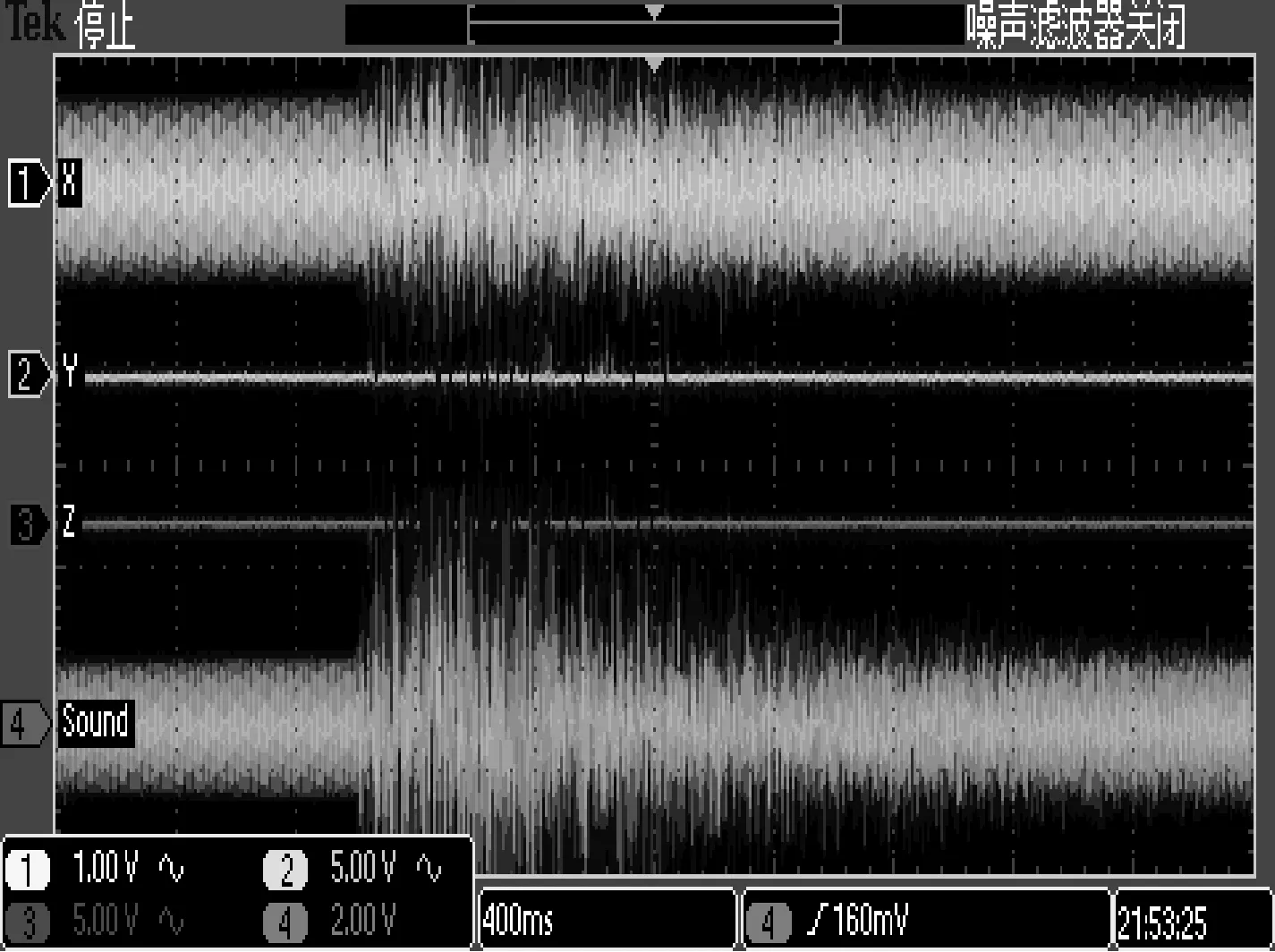
图13 突加闷雷干扰时的输出时序

由图13可见突加低频闷雷噪声干扰对变量y和z收敛波形影响轻微，说明Liu-cos电路板具有很好的抗突加窄带强噪声干扰能力。

6 性能对比

锁相放大器、Duffing混沌电路和Liu-cos混沌电路弱信号检测性能对比如表1。通过对比显示了Liu-cos混沌系统弱信号检测的优越性。

表1 弱信号检测性能对比

7 结 论

混沌系统对输入信号敏感、抗干扰性好，适合应用于声波弱信号检测领域。

(1)通过设计的混沌系统收敛性判别算法，证明了Liu-cos混沌系统变量y和z对于声波弱信号检测具有广域性收敛性、阈值唯一性。解决了传统Duffing混沌弱信号检测系统变量x和y输出不收敛、只能进入窄域检测等问题。

(2)实际声波检测实验显示Liu-cos混沌系统变量y和z具有广域检测性，收敛快，抗窄带干扰能力强；间歇混沌信号分界线明显、易于判别。

(3)对锁相放大器、Duffing混沌系统和三维Liu-cos混沌系统弱信号检测性能进行了对比，对比显示了三维Liu-cos混沌弱信号检测系统的诸多优点, 对未来混沌系统弱信号检测实际工程应用具有参考价值。

[参考文献]

[1] 聂春燕,石要武.基于混沌检测弱信号的混沌特性判别方法的研究[J].计量学报,2000,21(4):308-313.

[2] 衣文索,石要武,聂春燕.混沌态杜芬振子与弱正弦信号参量估计[J].计量学报,2006,27(2):156-159.

[3] 刘海波,吴德伟,金伟,等.Duffing振子微弱信号检测方法研究[J].物理学报,2013, 62(5):42-47.

[4] 时培明,孙彦龙,韩东颖.基于双耦合混沌振子变尺度微弱信号检测方法研究[J].计量学报，2016,37 (3):310-313.

[5] Lorenz E N.Deterministic nonperiodic flow[J].JAtmosScience,1963，20(2):130-141.

[6] Chen G,Ueta T. Yet another chaotic attractor[J].InternationalJournalofBifurca-tionandchaos,1999,9(7):1465-1466.

[7] 许喆,刘崇新,杨韬.一种新型混沌系统的分析及电路实现[J].物理学报,2010,59(1):131-139.

[8] Choe C U, Hohne K, Benner H,etal. Chaos suppression in the parame- trically driven Lorenz system[J].PhysRevEStatNonlinSoftMatterPhys,2005,72(3):036206.

[9] 孟玲玲,宋艳君,王晓东.基于变形Lorenz系统微弱周期信号频率检测新方法[J].计量学报,2013,34 (5):480-485.

[10] 刘剑鸣,杨霞,宋菲菲, 等.五种新混沌弱信号检测系统设计[J].计量学报,2016,37(5): 525-530.

[11] 刘剑鸣,杨霞,高跃龙, 等.类Liu系统在水声微弱信号检测中的应用研究[J].物理学报,2016,65 (7):070501.