二维声场的光学扫描方法

王浩宇, 冯秀娟, 祝海江, 何龙标,杨 平, 牛 锋, 王 敏(. 北京化工大学 信息科学与技术学院, 北京 0009; . 中国计量科学研究院, 北京 0009)

1 引 言

近年来,声光效应被广泛应用于水声领域[1,2]。声压的波动会导致介质折射率的改变,进而产生光衍射现象。当光束穿过时,其幅值和相位也会发生改变。实践表明,在音频段,声压远小于静压,光波的衍射效应可以被忽略[3]。

由于声光效应的存在,利用激光多普勒测振仪(laser Doppler vibrometer,LDV)重建声场的方法逐渐受到关注[4]。LDV发出的激光穿过声场,由于声场中空气折射率的改变,使得激光来回的光程差发生改变。因此,LDV解调出的速度与声压是相关的,可以通过这些速度数据重建声场的声压分布。相对于传统的传声器阵列法,光学法重建声场是一种非侵入的测量技术,它可以实现更高空间分辨力的声场重建。光学法重建声场的质量取决于重建的角度和空间分辨力[5],而这些因素又受到步进电机旋转间隔和平移间隔的影响。为了取得更高的重建分辨力就需要缩小扫描过程中步进电机的平移间隔和旋转间隔,结果是扫描耗时与重建声场的分辨力呈几何倍数增长。

本文在声场重建的理论基础上,提出一种新的扫描方案,可以在确保重建质量一定的条件下,优化扫描时间,提高声场重建效率。首先阐述声场重建原理,其次提出声场扫描方案,然后分析与比较仿真结果与重建结果,最后讨论了实验的影响因素。

2 声场重建原理

2.1 声光效应

声场的变化使周围空气的压强和密度随之发生变化,进而导致介质折射率变化。记pt和ρ分别表示空气总压强和密度,在绝热条件下,它们之间的关系可以表示为:

(1)

式中:γ为比热容比;p0和ρ0分别为静态条件下的空气压强和密度。而空气折射率n与密度ρ之间的关系可以由Gladstone-Dale方程给出:

n-1=Gρ

(2)

式中:G为常数。结合式(1)与式(2)可得:

(3)

式中:n0为标准大气压下的空气折射率;p为声压。考虑到声压远低于静压,因此对式(3)右端进行泰勒展开可得:

(4)

因此,当声压远小于静压时,介质折射率的变化与被测声压近似呈线性关系。

2.2 测量原理

设声场在扫描平面上的二维分布为p(x,y,t),当LDV发出的一束激光穿过声场时,其光程D可以表示为:

(5)

式中:L为光波的传输路径。可进一步得出LDV输出的等效速度:

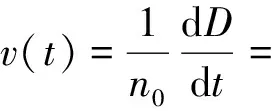
(6)

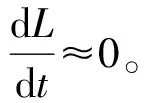
(7)

式(7)表明,激光测振仪输出的速度值与声压变化率的路径积分成正比,对式(7)两端进行傅里叶变换可得:

式中:Rp(x′,θ,ω)为声场P(x,y,ω)沿θ方向的投影积分,下标p表示该投影与积分路径上的声压。

2.3 声场重建原理

重建声场是一个逆问题,通过LDV输出的振动速度v(t)推算出空间中各点的声压p(x,y,t)。

如图1所示,声压p(x,y,t)沿L积分即是声场沿激光方向的投影Rp(x′,θ,t),这个积分在数学上被称作Radon变换:

旋转后的平面直角坐标系O′x′y′与原来的坐标系Oxy之间的关系为:

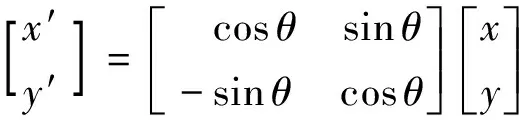
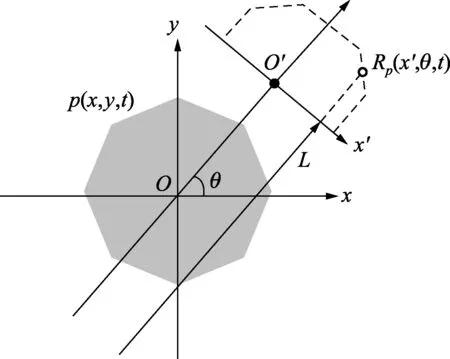
图1 平行束扫描方法得到声场的Radon变换

因此,在频域上可以利用Radon反变换求得P(x,y,ω):

P(x,y,ω)=R-1[Rp(x′,θ,ω)]=

利用反变换求出P(x,y,ω)后,进行傅里叶反变换即可求出时域声压p(x,y,t)。

3 声场扫描方法与测量结果

3.1 实验装置

实验设备搭建框架如图2所示,在计算机中设计Matlab控制与设备通信程序。

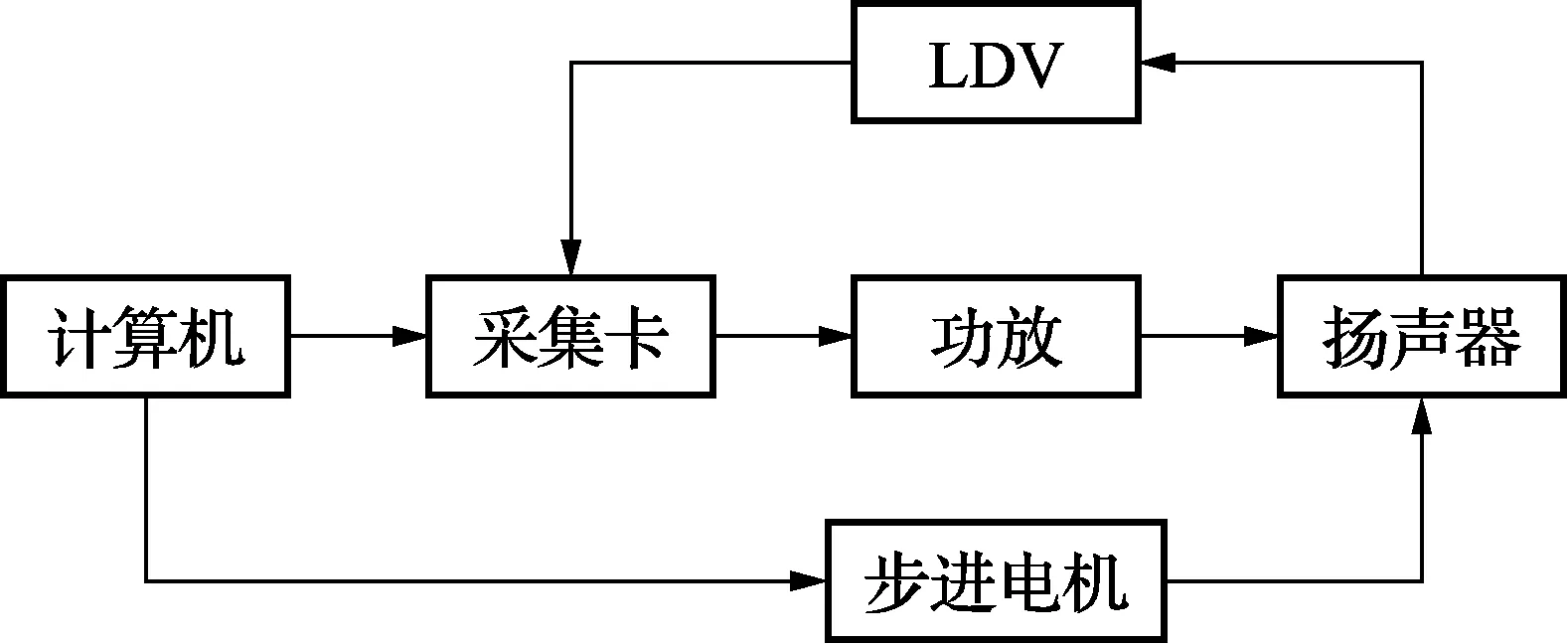
图2 声场扫描装置的构成

采集卡的输出信号作为声源驱动信号,通过功率放大器加载到扬声器上。由LDV发出激光穿过扬声器发出的声场,测量声波导致介质折射率的变化,输出与被测声压路径积分相关的等效速度,由计算机控制采集卡获取LDV的输出信号。图3是位于半消声室中的LDV、扬声器和反光镜,激光测振仪和反光镜固定在金属支架上,扬声器固定在运动电机上,由Matlab程序控制电机带动扬声器的运动。在计算机中搭建Matlab控制框架,通过扫描路径的控制、扬声器驱动信号的发射、LDV输出信号的采集和Radon反变换算法的同步控制,完成整个声场扫描过程。

图3 声场扫描装置

3.2 声场扫描方法

声场的二维重建质量取决于扫描的空间和角度分辨力。分辨力过低会使得重建得到的声场模糊不清,细节丢失；而分辨力过高又会导致重建过程极其缓慢，效率降低。因此,声场的重建需要在重建质量和重建效率之间折中。

计算机控制步进电机带动扬声器进行运动,整个扫描过程的所有运动都是由步进平移和步进旋转两种基础运动构成。首先,步进电机带动扬声器反向(激光器的左侧方向)移动至距离激光350 mm的负极大位置处,如图4(a)所示,随后计算机在该位置处进行采样时间为1 s的数据采集过程;之后进行正向(激光器右侧方向)步进平移运动,如图4(b)所示,运动步长设定为5 mm,且每次步进运动结束后计算机自动进行数据采集，直至扬声器运动至距离激光350 mm的正向极大位置处；电机带动扬声器进行逆时针的步进旋转,旋转步长设置为10°,如图4(c)所示;步进旋转完成后,扬声器从正极大位置处按相同的步长反向步进平移,直至运动到负极大位置处,如图4(d)所示。周期性重复步进平移和步进旋转运动,直至扬声器旋转至170°,整个扫描过程结束。

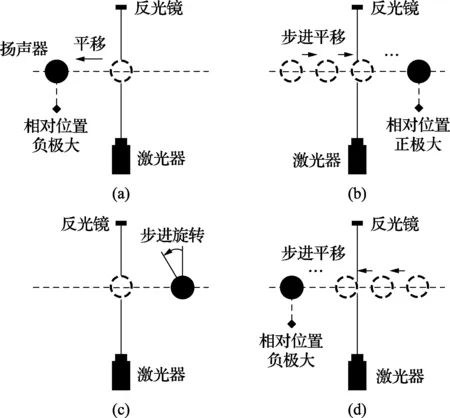
图4 声场扫描方案

在整个扫描过程中,扬声器在每个角度位置处,以5 mm为平移运动步长,从-350 mm运动至350 mm,总计平移140次;以10°为旋转运动步长,从0°旋转至170°,总计旋转17次;计算机采集LDV的数据总计2 538次,整个实验过程耗时约为2.5 h。

3.3 实验结果与讨论

3.3.1 瞬时声压分布的仿真结果

利用Matlab进行声场仿真,声源频率设为 2 kHz, 类型是点声源,模拟在距声源平面16.5 cm的平面上的声压分布,重建区域是-0.25～0.25 m的正方形平面,结果如图5所示。

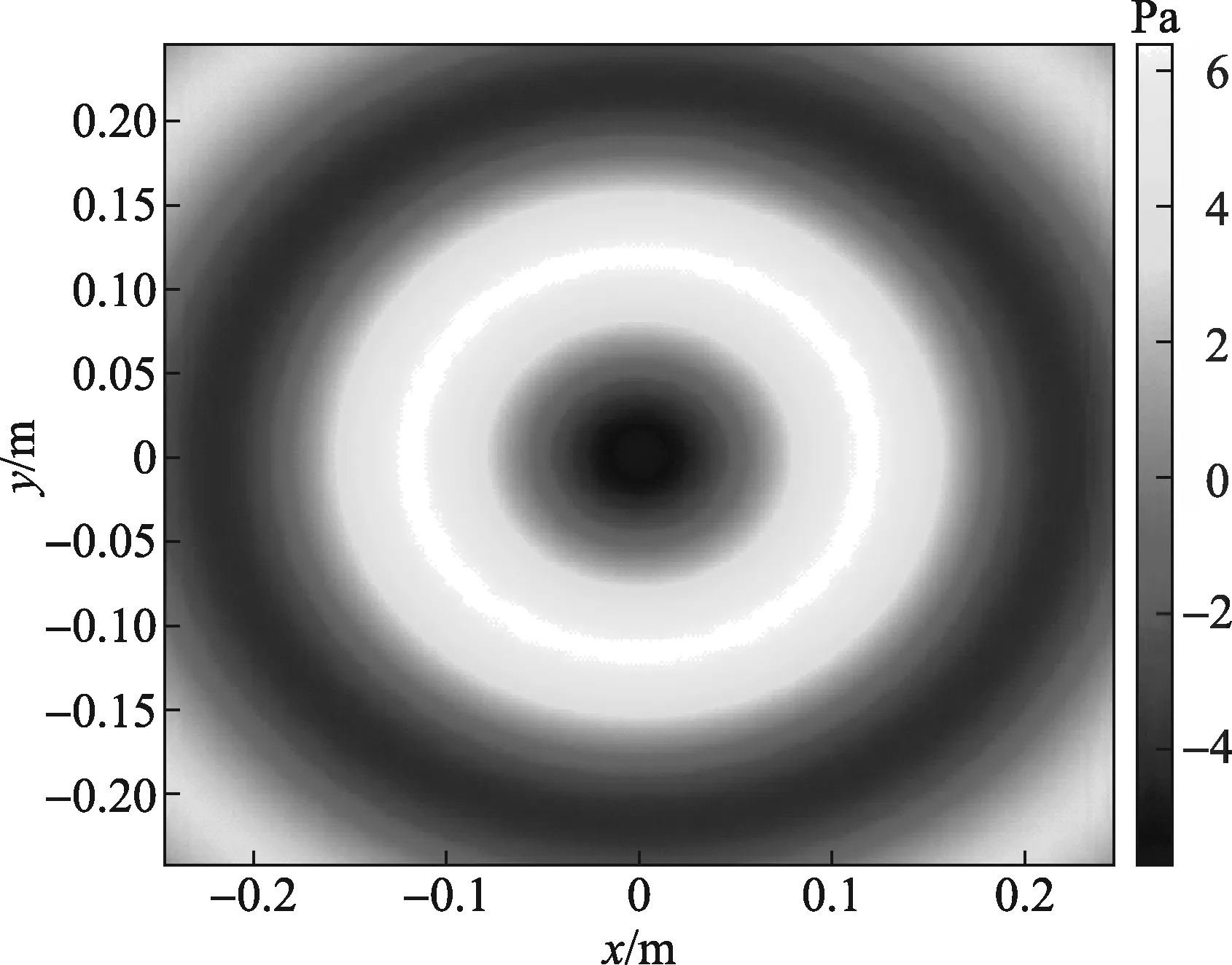
图5 瞬时点源声场的仿真

对该平面的声压进行Radon变换得到图6所示的分布图。由于点声源在被测平面上呈中心对称,因此声场经过Radon变换后的投影分布,不随旋转角θ的变化而变化。

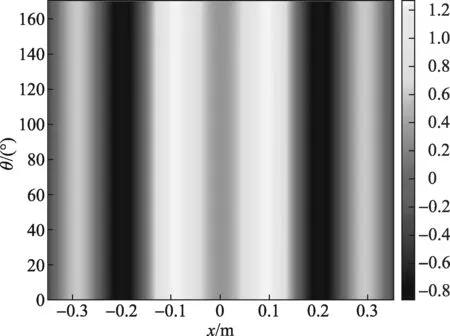
图6 瞬时点源声场的Radon变换仿真

实际测量过程中,旋转角θ和水平位移x是离散变化的,重建声场的效果与旋转步长Δθ和平移步长Δx有关。当设定旋转步长Δθ=10°、平移步长Δx=5 mm时,声场的重建结果如图7所示。

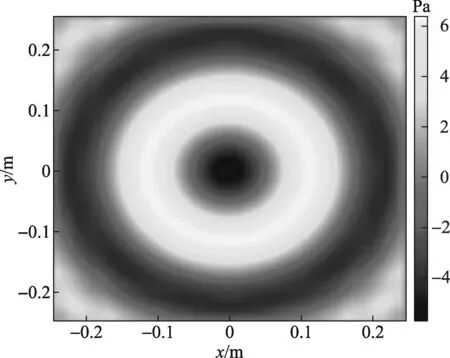
图7 瞬时声场声压分布的仿真结果(空间分辨力5 mm,角度分辨力10°)

3.3.2 瞬时声压分布的实验结果

实验过程中,设定扬声器驱动信号频率为2 kHz,峰峰值为4 V的正弦信号,通过Matlab平台控制信号发送与采集的同步触发,实现瞬时声压的扫描。LDV发出激光的光束直径为2 mm,激光测振仪得到的各位置和各角度的等效速度分布如图8所示,声场引起介质折射率变化产生的等效速度范围为0～10 mm/s。利用Radon反变换得到的声压在空间上的二维分布如图9所示。

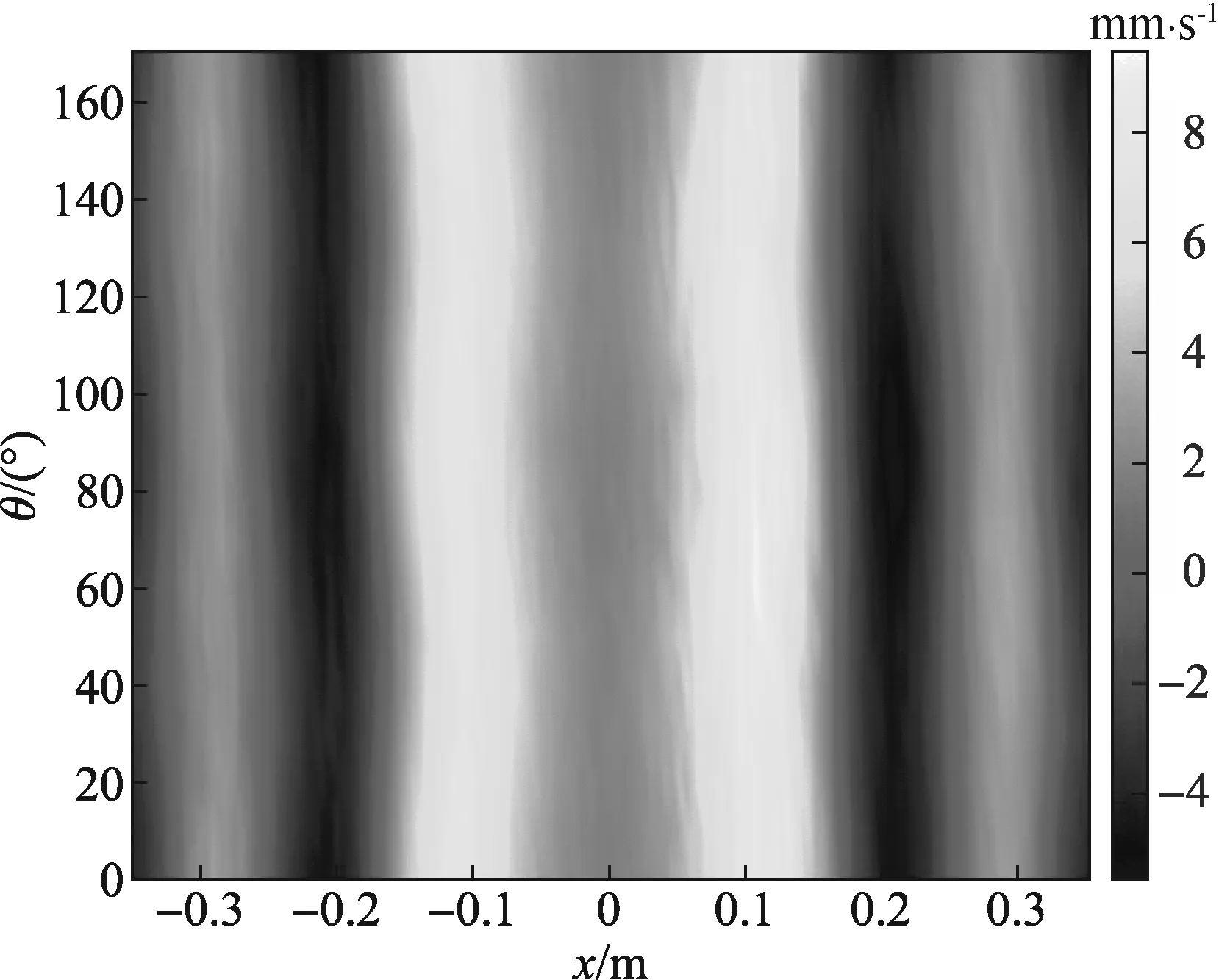
图8 LDV测得的各位置处瞬时速度

图9 被测声场的声压分布实验结果(空间分辨力5 mm,角度分辨力10°)

通过调整运动电机平移和旋转运动的步进间隔重复实验,分别得到空间分辨力为10 mm、角度分辨力为10°和空间分辨力为10 mm、角度分辨力为20°的重建图像,如图10、图11所示。

图10 被测声场的声压重建结果(空间分辨力10 mm,角度分辨力10°)

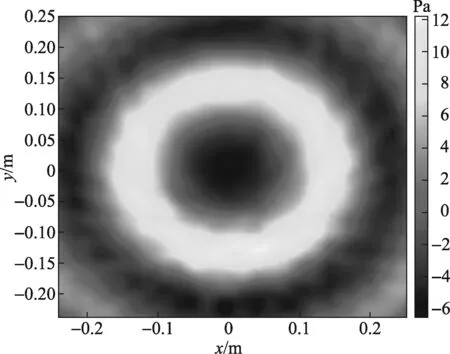
图11 被测声场的声压重建结果(空间分辨力10 mm,角度分辨力20°)

3.3.3 结果讨论

实验结果表明,利用声光效应测量声场声压的二维分布是可行的,且重建声压呈中心对称,符合点声源的声压分布规律。通过对比图7与图9可知,实际测量得到的图像并没有仿真图像那样‘纯净’,因为在实际测量过程中,影响测量结果的因素有很多,比如环境中不稳定的噪声干扰、反光镜的振动、温度梯度的存在等等。通过对比图9、图10和图11可以看出：重建分辨力小,会使得图像模糊,细节丢失;而重建分辨力又受到激光直径的限制,如果空间分辨力高于激光直径,激光就无法看做是理想的线性光束。因此,需要保证空间分辨力低于激光光束直径。

传统的传声器法测量声压逐渐成熟,广泛应用于空间点的声压测量中。而目前基于声光效应的光学法是依据LDV测得的声压投影积分通过反Radon变换得出声压的空间分布信息。在反Radon变换过程中,使用不同的滤波算子(比如,Hann滤波、Cosine滤波等)得出声压分布的数值会有所变化,所以,目前光学法更侧重于定性描述声场声压的二维分布信息。

4 结 论

本文研究了基于声光效应测量的声场扫描方法。通过模拟仿真和实际测量结果表明声光效应可以用来重建声场。LDV测得的速度实际上是由声光效应引起的,它是声压在激光传播方向上的投影积分。利用平行束扫描在各个方向上得到的投影积分通过反Radon变换可以重建声场的二维分布。本文实现了一种高效、快捷的声场扫描方法,通过该方法可重建出声场的空间分辨力为 5 mm, 角度分辨力为10°,被测量声场的最大声压为12.6 Pa。实验表明,这种扫描方案对于声场的二维重建是可行的,可用于声学换能器辐射声场参数的测量和评估,为声学换能器的设计提供一种新的辅助手段。

[参考文献]

[1] Buick J M, Cosgrove J A, Douissard P A,etal. Application of the acousto-optic effect to pressure measurements in ultrasound fields in water using a laser vibrometer[J].ReviewofScientificInstruments, 2004, 75(10): 3 203-3 207.

[2] Harland A R, Petzing J N, Tyrer J R. Nonperturbing measurements of spatially distributed underwater acoustic fields using a scanning laser Doppler vibrometer[J].TheJournaloftheAcousticalSocietyofAmerica, 2004, 115(1): 187-195.

[3] Theobald P D, Robinson S P, Hayman G,etal. Acousto-optic tomography for mapping of high-frequency sonar fields[J].TheJournaloftheAcousticalSocietyofAmerica, 2008, 123(5): 3 437-3 437.

[4] Fernandez-Grande E, Torras-Rosell A. Three-dimensional reconstruction of sound fields based on the acousto-optic effect[J].TheJournaloftheAcousticalSocietyofAmerica,AcousticalSocietyofAmerica, 2013, 134(5): 3 998-3 998.

[5] Torras-Rosell A, Barrera-Figueroa S, Jacobsen F. Sound field reconstruction using acousto-optic tomography[J].TheJournaloftheAcousticalSocietyofAmerica, 2012, 131(5): 3 786-3 793.

[6] Rosell A T, Figueroa S B, Jacobsen F. An investigation of sound fields based on the acousto-optic effect[C]// International Congress on Sound and Vibration 2011 (ICSV18) 18th. 18th International Congress on Sound and Vibration 2011. Rio de Janeiro, Brazil, 2011.