阿伏加德罗常数测量与千克重新定义

罗志勇, 王金涛, 刘 翔, 李占宏(中国计量科学研究院, 北京 100029)

1 引 言

当前, 国际计量领域正在进行深刻变革[1]。现行的千克定义生效于1889年, 它指定一个人造的圆柱体砝码(称为“千克原器”, 直径和高度均为39 mm的铂铱合金)的质量为1 kg。然而研究发现, 千克原器的质量到目前为止发生了约50 μg 的漂移, 这与基本单位定义应具有高度稳定性和恒定性的属性相矛盾, 阿伏加德罗常数(Avogadro constant)NA和普朗克常量h被认为是有望用于重新定义千克的2个基本物理常数,国际计量局预期在2018年第26届国际计量大会(Conference Generale des Poids et Mesures,CGPM)上通过关于国际单位制(SI)包括质量单位修订的决议。

2 阿伏加德罗常数及其测量

阿伏加德罗常数的测量采用X射线晶体密度(X-ray crystal density, XRCD) 法[1]:

式中:n为晶胞粒子数;r为硅球半径;m为硅球质量;M为硅原子量;a为晶格常数。因此只要测定单晶硅的原子量(数值上等于硅的摩尔质量),单晶硅球的宏观密度(硅球的质量除以体积),晶胞的体积(晶格常数和晶胞原子数),就可以求得阿伏加德罗常数。

2.1 单晶硅材料及其基本参数

由于晶体具有规则的周期性结构,单晶硅晶格具有极其稳定和近乎理想立方体结构,因而被用作NA测量的首选材料[2,3]。

2.1.1 高纯度浓缩28Si单晶硅

自然单晶硅材料含有3种同位素:28Si,29Si,30Si。为了提高硅原子量测量准确度,通过对自然硅浓缩使28Si的丰度比已大于99.99%,通过特殊生长工艺更严格控制单晶硅以碳、氧、氮为主的杂质及晶格缺陷,杂质含量、晶格缺陷的质量比可以控制在 4×10-9～5×10-9。

2.1.2 硅原子量测量

根据单晶硅的3种同位素组成,其摩尔质量为:

MSi=f28M28+f29M29+f30M30

(1)

式中：fi(i=28,29,30)为3种同位素的丰度,且∑fi=1;Mi为摩尔质量。要精确测出各个同位素的原子量之外,还要精确测出它们的丰度。目前,3个同位素各自的摩尔质量测量不确定度均已优于1×10-8,28Si的摩尔质量测量甚至优于10-9。5 kg28Si单晶硅材料已被应用于NA测量, 德国技术物理研究院(PTB)浓缩单晶硅原子量的测量不确定度已达到1.7×10-9,主要误差来源是硅同位素的丰度比。

2.1.3 单晶硅晶格常数测定

晶格常数的测量是通过X射线/光学组合干涉仪实现[4],其原理是将3个单晶硅薄片平行放置,其中一边镜片可以实现竖直方向的移动,用激光干涉仪可测得其运动的位移。当一束X射线倾斜入射到另一边晶片上时,利用衍射效应重叠产生的干涉效应,即可探测到干涉条纹信号从而测量晶格常数,晶格常数的测量不确定度已达到3×10-9。

2.2 硅球制造

精密球制造技术的关键在于碾磨, 碾磨包括切削、初磨、精磨和抛光过程。 精密球的2个主要技术指标是球度与表面光滑度, 不仅依赖球磨装置技术参数、控制工艺, 也与球的制造材料密切相关。相比较于晶体等具有方向差异的材料, 各向同性的均质材料(如玻璃等)则容易实现更高的球面度和表面光滑度。

美国国家标准技术研究院(NIST)、德国技术物理研究院(PTB)、英国国家物理实验室(NPL)、中国航天精密机械研究所及澳大利亚联邦科学院(CSIRO)都具有较高的磨球技术, 其中澳大利亚CSIRO及德国PTB 研制的自动磨球装置, 均可实现对单晶硅球的高精度碾磨, 球度已达到20 nm, 完全可以满足阿伏加德罗常数研究和用于重新定义质量单位千克的需要。

2.3 硅球绝对密度

绝对测量法是指根据密度的定义(密度=质量/体积), 通过测量单晶硅的质量和体积即得到密度,硅球直径的测量是最核心技术。

2.3.1 硅球直径的测量

用激光干涉仪测量硅球直径,其实验装置基本原理如图1所示。

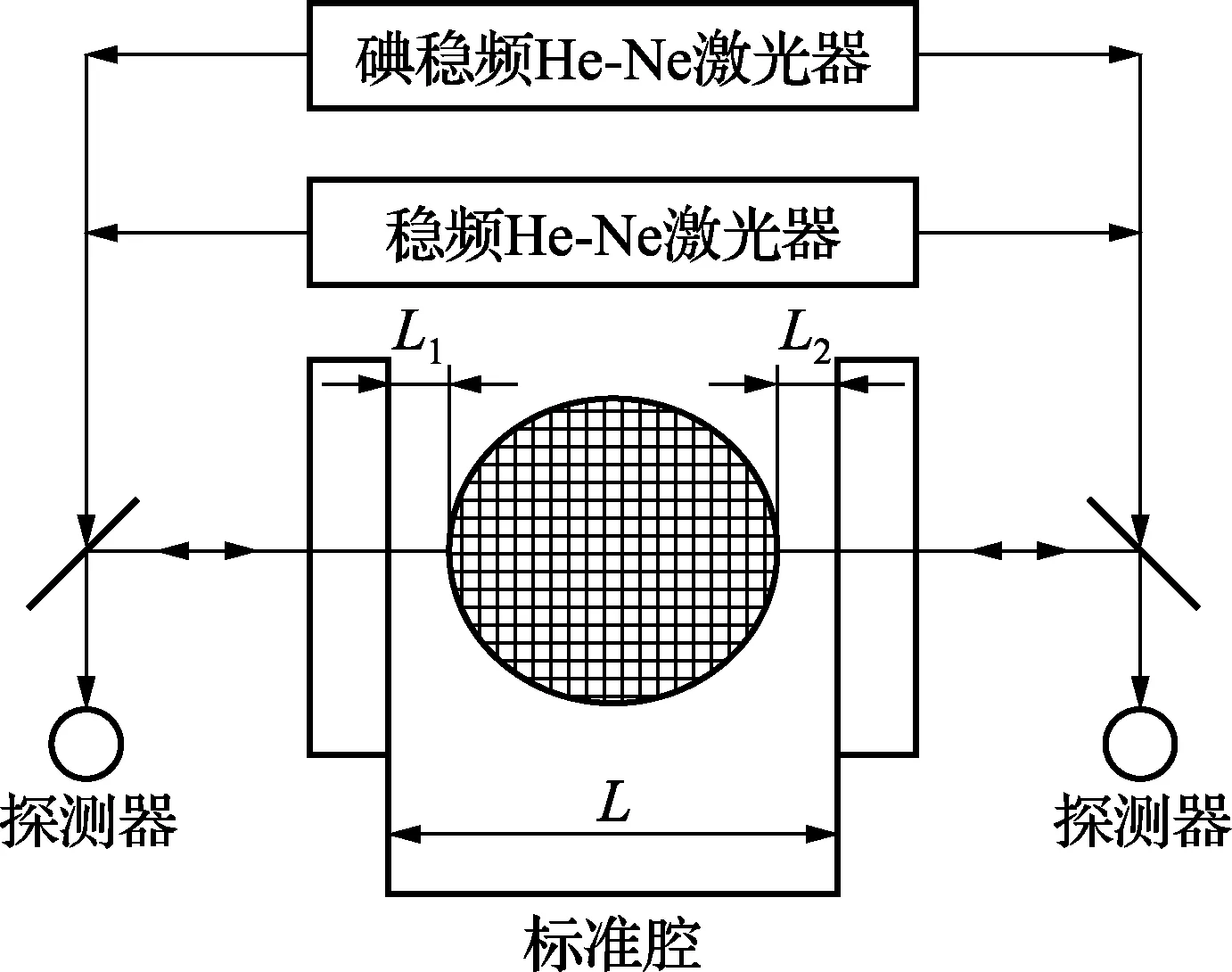
图1 硅球直径测量原理

硅球直径D=L-(L1+L2),其中L,L1,L2通过相移干涉法实现。按照其实现方式有两条技术路线:激光变频相移干涉法[5,6]和机械扫描相移干涉法[7～12]。前者利用可调谐半导体激光,通过热源控制谐振腔腔长实现输出激光的波长改变进而实现相移。基于变频的相移干涉有2个重要特征:一是L,L1,L2的初值必须已知(精确到微米或亚微米级)；二是变频激光器除了足够的变频宽度还必须具有极高的频率稳定性和极高的强度稳定性。后者机械移动实现绝对相移,不需要初测L,L1,L2,由于不需要变频可以选择性能优越的激光器作为光源,此外半导体变频激光器的造价大约是普通高性能激光器的数十倍。激光变频相移干涉法已经发展出基于平面标准具的激光变频相移干涉法和基于球面标准具的测量方法。2011年,Kuramoto等[5,13]利用平板Etalon将硅球直径不确定度提高到2.3 nm。球面干涉仪方案最早由Nicolaus 等于1997年提出, 后在测量系统上几经改进, 2010年, 日本国家计量院(NMIJ)、德国PTB 和澳大利亚国家计量院(NMIA)3个计量技术机构进行了硅球直径测量的比对(不考虑硅球表面氧化层的影响), 不确定度分别评估为1.12, 0.98 ，2.39 nm, 比对结果的最大偏差不超过2 nm。 目前包括我国在内硅球直径的测量不确定度已优于1 nm,相关的研究仍在继续深入进行。

2.3.2 硅球表面氧化层的测量

实验中使用的硅球并非完全由单晶硅组成,而是在硅球的表面附着一层透明的自然氧化层, 这是由于单晶硅在自然环境中不可避免地会发生氧化产生的。 该氧化层对硅球密度测量的影响,主要体现在使激光干涉仪的干涉条纹产生相位偏移, 导致直径测量误差[14]。因此氧化层质量必须从硅球质量中扣除。氧化层测量方法包括光谱椭偏术、卢瑟福后向散射能谱法、透射电子显微镜、X 射线反射术和X 射线光电子能谱术等方法等等。近年来德国PTB已将氧化层测量的不确定度降低到0.30 nm。

2.3.3 硅球质量测量

硅球的吸气、放气总量可达基准球体积的 10%～100%, 硅球表面杂质、污染、水分含量等成为影响硅球质量测量的主要因素。经过多年的研究,影响质量测量的主要因素已大幅减小或基本消除,2008年硅球质量测量国际比对主要结果的一致性优于1×10-8,其中BIPM对硅球质量的测量不确定度已经达到5×10-9。

3 千克的重新定义

新的千克定义可表述为[15]:

普朗克常数的测量值h,随着实验的不断深入会有一定程度的修正。但无论在实验的任何阶段,h一经固定,质量单位千克的值就固定不变。

3.1 基于原子计数法(阿伏加德罗常数)的表述

普朗克常数可以通过功率天平实测得到,也可以通过摩尔普朗克常数(molar Plank constant)实测阿伏加德罗常数得到,即NAh=3.990 312 711 0×10-10J·s·mol-1,标准不确定度为0.000 000 001 8×10-10J·s/mol或相对标准不确定度为4.5×10-10(摩尔普朗克常数具有极高的准确度,相比对NA或h可以视为常数)[16],也可通过固定阿伏加德罗常数的值获得千克单位。

3.2 基于新定义千克复现

当采用自然常数定义新千克之后,千克单位的量值复现将成为最紧迫的任务。对原子计数法而言,同一批次生产的单晶硅球,由于阿伏加德罗常数测量中晶格常数和原子量及其晶格缺陷一经测定就固定不变,因此采用原子计数法复现千克实际上就是复现单晶硅球的质量[1]:

(2)

式中:Ms为硅球的复现质量;me为电荷质量;M为浓缩硅的平均原子量;Vc为硅晶体积;md为晶格空穴质量损失;mSL为硅球氧化层的质量。

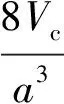
需要注意的是通过长期以来对硅球表面氧化层的结构研究,其一氧化硅分布层、杂乱晶体分布层对光学参数的影响并不明显,氧化层模型[1]基本可以简化成表面水分层、环境或操作污染层、二氧化硅层和硅晶核心层。表面水分层、污染层可通过清洗工艺减小或消除,二氧化硅层测量的基本原理仍以传统椭圆偏振法测量,表面状态测量、监测、评估设备也都是商业有效的成熟系统。其次,用于复现千克质量的单晶硅球应由国际阿伏加德罗常数工作组协调和制造,包括晶体材料的选取、同位素浓缩、晶体生长和硅球的碾磨技术和工艺控制等等,这样同批次的硅球空穴和杂质含量是经过分析和测量的,并作为硅球的固有参数永远不变[1],但对不同批次的材料必须分别进行空穴和杂质含量的分析测量。

4 结论及展望

利用XRCD方法测量阿伏加德罗常数与利用功率天平测量普朗克常数方法的一致性已达到5×10-8,并正接近2×10-8。 为了保证基本单位定义的可延续性[14], 基本单位的重新定义还要求定义后的复现不确定度不差于现行定义的复现不确定度。根据 2005 年国际计量委员会第 94 次会议的建议, 重新定义千克的条件之一是复现不确定度不大于 2×10-8, 即基本物理常数的不确定度也应优于 2×10-8, 这正是当前NA测量的阶段性目标。长远的目标,从理论上讲阿伏加德罗常数的测量不确定度甚至可以达到并优于1×10-8。

[参考文献]

[1] Fujii K, Bettin H, Becker P,etal. Realization of the kilogram by the XRCD method[J].Metrologia, 2016, 53(5): A19-A45.

[2] Becker P. The new kilogram definition based on counting the atoms in a28Si cystals[J].ContemporaryPhysics, 2012, 53(6): 461-479.

[3] Becker P, Pohl H J, Riemann H,etal. Enrichment of silicon for a better kilogram[J].PhysicaStatusSolidi,2010, 207(1):49-66.

[4] Andreas B, Azuma Y, Bartl G,etal. An accurate determination of the Avogadro constant by counting the atom in a28Si crystal[J].PhysicalReviewLetters, 2011, 106: 030801.

[5] Kuramoto N, Azuma Y, Inaba H,etal. Volume measurement of28Si spheres by an optical interferometer with a flat etalon to determine the Avogadro constant[J].Metrologia, 2011, 48(2):S83-95.

[6] Azuma Y, Barat P, Bartl G,etal. Improved measurement results for the Avogadro constant using a 28Si-enriched crystal[J].Metrologia, 2015, 52(2):360-375.

[7] LUO Z Y, GU Y Z, ZHANG J,etal. Interferometric Measurement of the Diameter of a Silicon Sphere With a Mechanical Scanning Method[J].IEEETransactionsonInstrumentationandMeasurement, 2010, 59(11):2991-2996.

[8] LUO Z Y, LI Z H. A new route for length measurement by phase-shifting interferometry[J].ScienceChina(Physics,Mechanics&Astronomy),2012, 55(4):599-604.

[9] 罗志勇. 质量自然基准的研究进展及发展方向[J]. 计量学报, 2004, 25(2): 138-141.

[10] 罗志勇, 杨丽峰, 顾英姿, 等. 阿伏加德罗常数测量中单晶硅密度的绝对测量[J]. 计量学报, 2008, 29(3):211-215.

[11] 罗志勇. 单晶硅球密度的绝对测量[J]. 计量学报, 2012, 33(5):428-431.

[12] 罗志勇, 杨丽峰, 陈允昌. 标准硅球直径精密测量系统的设计[J]. 计量学报, 2005, 26(4): 289-294.

[13] Andreas B, Fujii K, Kuramoto N,etal. The uncertainty of the phase-correction in sphere-diameter measurements[J].Metrologia, 2012,49:479-486

[14] 李岩, 张继涛, 罗志勇.阿伏加德罗常数测量与千克重新定义[J]. 科学通报, 2011, 56(10):717-724.

[15] Davis R, Barat P, Stock M. A brief history of the unit of mass: continuity of successive definitions of the kilogram[J].Metrologia, 2016, 53(5):A12-A18:

[16] BIPM. 2014 CODATA recommended values[EB]. http://www.bipm.org/en/bipm/mass/avogadro,2017-08-11.