基于非线性耦合双稳态随机共振的轴承微弱故障信号增强检测方法研究

时培明， 孙 鹏， 袁丹真(燕山大学电气工程学院, 河北 秦皇岛 066004)

1 引 言

滚动轴承是机械设备中的重要旋转零件，也是机械设备主要故障源。研究滚动轴承微弱故障信号的检测在了解轴承的性能状态和及早发现潜在故障等方面起着至关重要的作用，具有重要的实践意义[1～3]。轴承早期的故障特征很微弱，现在的微弱特征提取方法更多的是从消除噪声方面进行故障检测，例如基于小波变换[4]、模式分解[5]降噪方法。尽管以上方法能在一定程度上检测出故障特征，但削弱噪声的同时把有用信号也削弱了。

随机共振研究最早始于20世纪80年代初，由Benzi R等人和Nicolis C等人在研究古代冰川气候问题时发现。对于许多非线性系统，适当的噪声可以有助于提高系统的输出信号的能力，并被称为随机共振的非线性现象。在理论上，人们主要是利用用Langevin方程和Fokker-Planck方程来讨论随机共振的各种统计性质，并逐渐形成了随机共振的绝热近似理论[6]和线性响应理论[7]，但尚未成熟仍在不断发展。目前，随机共振现象主要是基于物理实验和模拟观测得到。1983年，Fauve和Heslot[8]在实验研究施密特触发器中首次证实了随机共振现象的存在。1988年，Mc Namara[9]等人在双稳态激光器中观察到随机共振现象的存在。这种现象的发生需要3个条件：(1)弱周期信号；(2)噪声源；(3)非线性系统。只有当非线性双稳态系统和周期信号、噪声源相互匹配时可以产生随机共振现象。

以前大多研究在单一稳定系统的随机共振[10,11]或者在线性系统下的随机共振现象[12～15]。对由非线性耦合双稳态二阶系统随机共振系统和在轴承故障诊断方面的应用较少，并且以信噪改善比作为随机共振是否产生的依据研究较少。在本文中，以耦合双稳系统[16]为模型，利用信噪改善比(signal to noise improvement ratio，SNIR)[17]和相关系数[18]特性曲线作为随机共振是否产生的一个理论依据。

本文提出了一种新型非线性耦合双稳态系统模型并给出了耦合方程，通过势函数表达式画出了其三维图，并分析了随机共振产生的机理。然后通过改变系统模型中的参数，画出信噪改善比和相关系数随参数改变的曲线图。通过实际轴承故障数据对模型进行实例分析，发现此模型能够对轴承微弱的故障信号进行有效捡测。

2 耦合双稳态随机共振模型

由两个单一的双稳态系统经非线性耦合而成的耦合随机共振模型如下：

Asin(2π×0.02t)

(1)

(2)

式中：r代表阻尼系数；k是耦合系数；a1,b1,a2,b2是系统参数；A≪1；ζ是噪声，并且满足自相关函数

〈ζ(t)ζ(s)〉=D2δ(t-s)

(3)

式中：D是噪声强度。

当非线性双稳态系统和周期信号、噪声源相互匹配时可以产生随机共振现象，该耦合系统的势函数v(x,y)可表示为

(4)

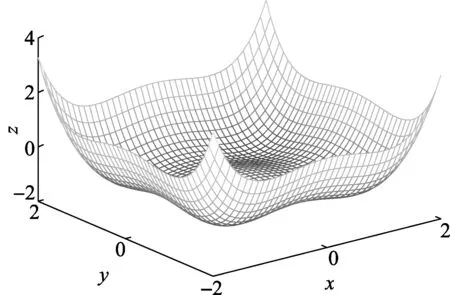
图1 势函数三维图(a1=1，b1=1，a2=1，b2=1，r=0.01)

如图1所示,当a1=1，b1=1，a2=1，b2=1，r=0.01时，可以看到有4个势阱，且相互对称，势垒处于中心位置。但是随着弱周期信号加到耦合系统中，系统平衡被打破，势函数会随着驱动力发生周期性变化，势垒高度也会发生变化，由于周期信号能量太弱，布朗粒子的能量太小，使其只能在单一势阱内运动。随着噪声的加入，使布朗粒子能量增大，可以使其越过势垒到达另一势阱，当运动周期等于微弱信号周期时发生随机共振现象。由于周期信号和噪声只作用于x方向，因此只有在x方向或者在x方向比y方向更有利于产生随机共振现象。耦合系数将影响耦合系统势函数结构，适当耦合系数会对系统随机共振产生有利影响。

3 耦合双稳态系统特性分析

数值仿真采用4阶龙格库塔算法，对于式(1)、式(2)来说，不同参数的取值，将出现不同的随机共振特性。为定量分析随机共振现象，把信噪改善比响应特性曲线(SNIR)和相关系数作为随机共振是否产生的依据，其SNIR值大于1被认为是随机共振系统对输入信号产生积极作用的标志。Makra等人认为随机共振可以提供信噪比增益，证实可以获得大于1的信噪改善比。其定义如下：

(5)

即输出信噪比SNRo与输入信噪比SNRi之比。

信噪比指的是信号的有效值S与噪声的有效值N之比。其定义如下：

(6)

相关系数也可以作为随机共振的评价方法，它描述了两个随机变量之间线性相关的程度。输出信号x(t)的自功率谱密度为：

(7)

式中：Rxx(τ)为x(t)的自相关函数。

系统的输入输出互功率谱为：

(8)

式中：Rxy(τ)为x(t)与故障信号y(t)的互相关函数。相关系数定义为：

(9)

下面分别讨论耦合系数k，阻尼系数r对随机共振产生的影响。

(1)如图2、图3所示，分别画出了当a1=1，b1=1，a2=1，b2=2，r=0.7，k=0和k=0.7时的信噪改善比曲线图与相关系数曲线图。通过两个曲线图都可以观察到耦合的作用，促进了信号、噪声和系统之间的协同作用，更有利于随机共振现象的发生。

(2)如图4所示，在对应k=0.5，a1=1，b1=1，a2=1，b2=1，不同的r值在x方向上的信噪改善比曲线图。可以看到，随着噪声强度的增加，信噪改善比的值先增加后减小，出现了一个峰值，这正是随机共振发生的一个重要特点。

图2 信噪改善比曲线 (a1=1，b1=1，a2=1，b2=2，r=0.7)

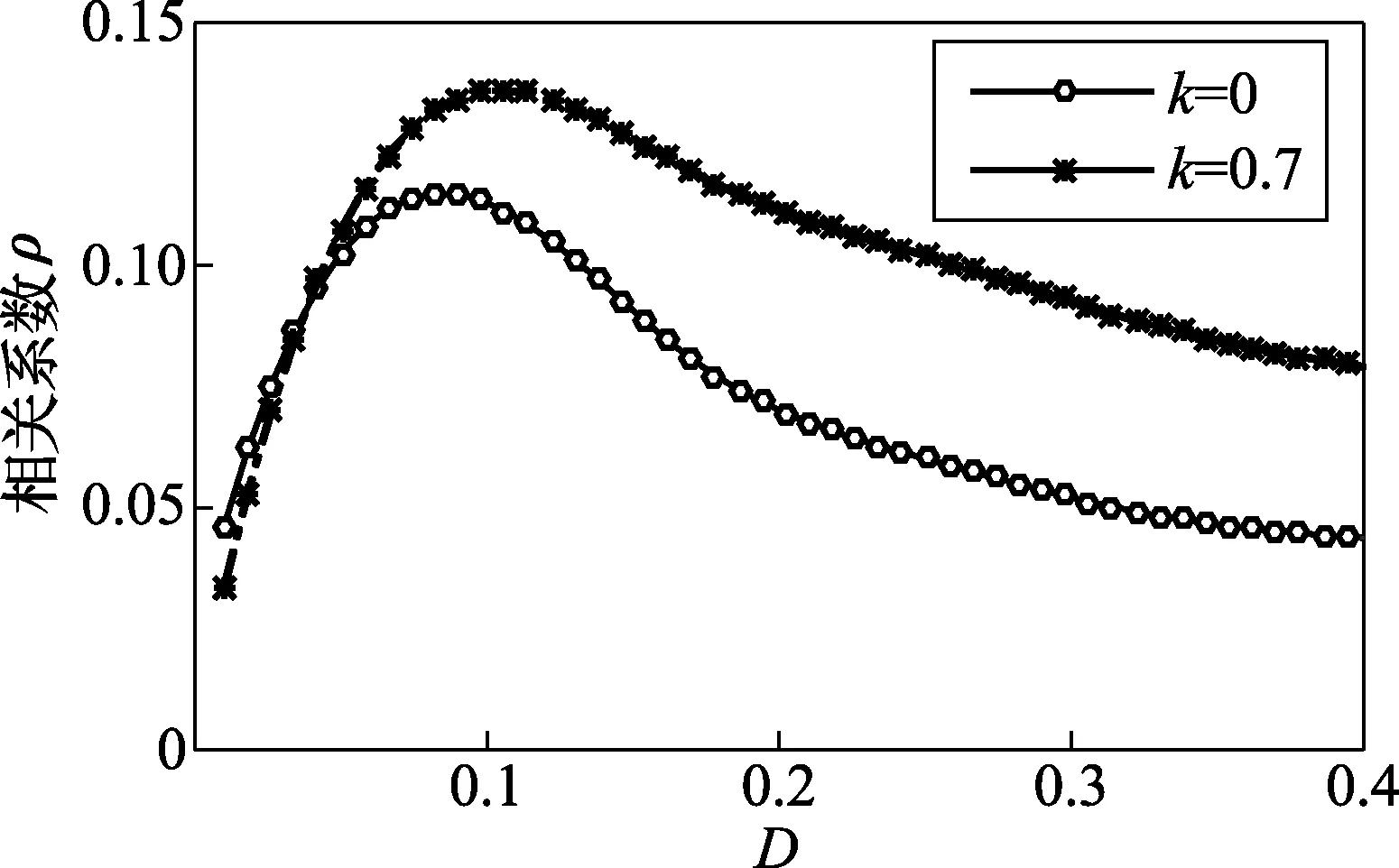
图3 相关系数曲线(a1=1，b1=1，a2=1，b2=2，r=0.7)

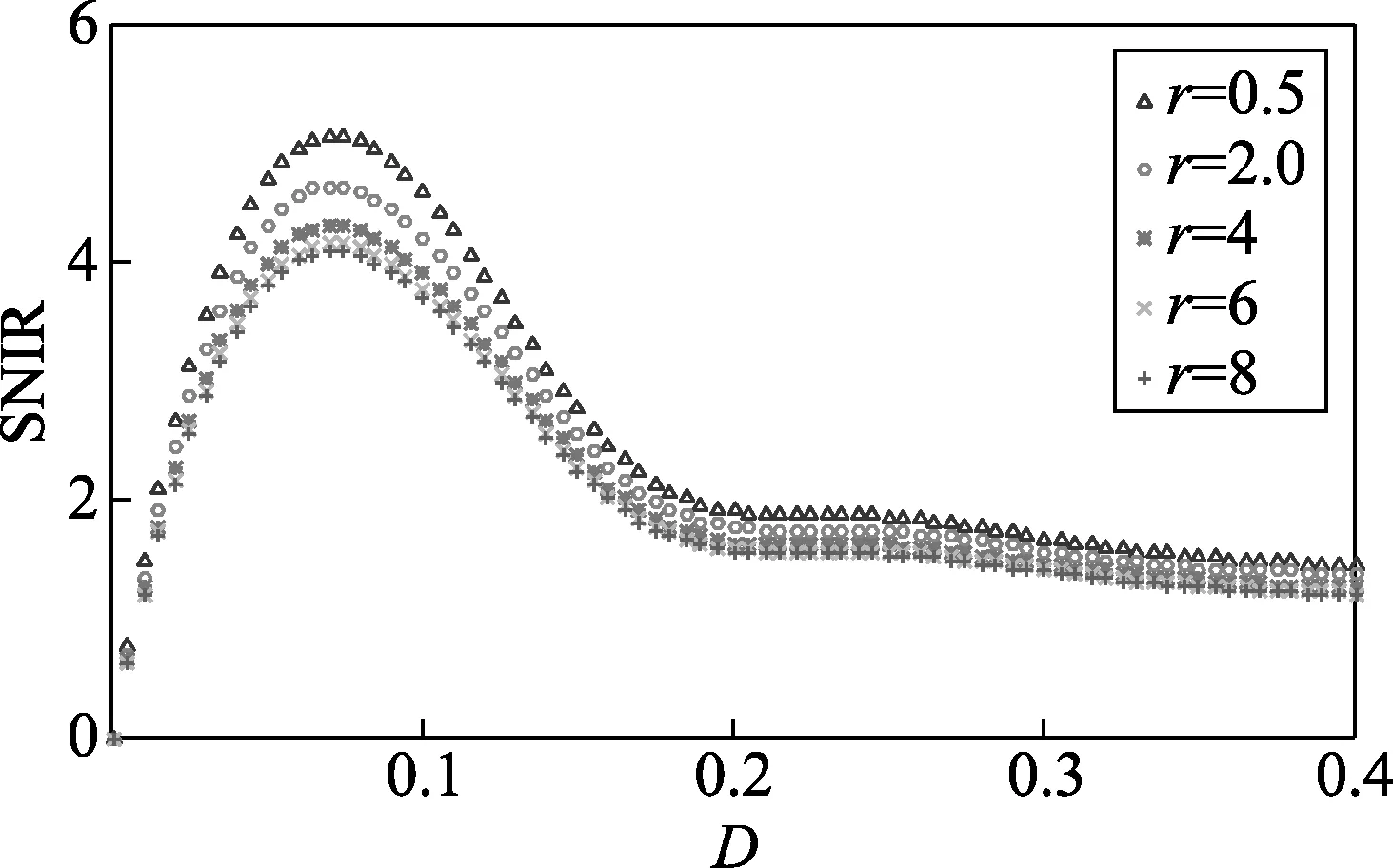
图4 信噪改善比曲线(k=0.5，a1=1，b1=1，a2=1，b2=1)

4 实例验证

对于驱动端轴承，其型号为SKF6205-2RSJEM，采样频率为12 kHz，转速为fr=1 772 r/min，驱动端滚动轴承尺寸信息如表1所示，滚动轴承负载1.5 kW时各部件的故障特征频率如表2所示。

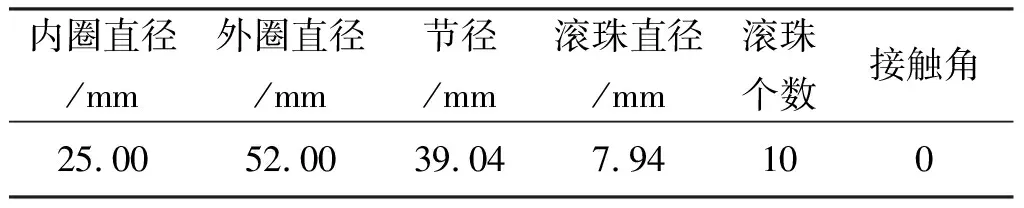
表1 驱动端轴承尺寸信息

表2 驱动端滚动轴承各个部件的故障特征频率

图5 故障轴承的时域图和功率谱图

以滚动体故障为例，通过计算得其理论特征故障频率为119.72 Hz，其时域图和功率谱图如图5所示。利用随机共振方法对其进行检测，通过随机共振处理后得出滚动轴承滚动体发生故障时的时域图和功率谱图如图6所示。

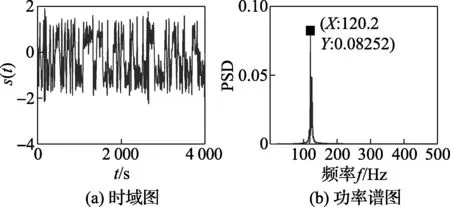
图6 输出信号的时域图和功率谱图

图5、图6中所标出的是频率为120.2 Hz时的坐标值，与理论计算中的滚动体故障频率119.72 Hz相吻合，还可以看出一些高频成分被消弱，而有用信号得到加强，特征频率120.2 Hz处的幅值由0.014 9增加到0.082 52，有了很大提高。从而可以判断此故障为轴承滚动体故障。

5 结 论

本文提出了一种新型耦合随机共振的微弱轴承故障信号检测方法。首先，由势函数图形分析，随着噪声强度增加，会使粒子在两个势阱之间运动，当非线性双稳态系统和周期信号、噪声源相互匹配时会产生随机共振现象。然后，用信噪改善比和相关系数曲线去验证了增加耦合项能够加强随机共振现象的发生。同时，画出了阻尼系数随着噪声强度变化的信噪改善比曲线图，发现在某个噪声强度下，它的信噪改善比值达到一个最大值，它是随机共振产生的一个明显特征。并且对实际轴承故障信号进行处理，证明了非线性耦合双稳态系统能增强故障特征信号。

[参考文献]

[1] Xue H, Wang H, Chen P,etal. Automatic diagnosis method for structural fault of rotating machinery based on distinctive frequency components and support vector machines under varied operating conditions[J].Neurocompution, 2013, 116: 326-335.

[2] Randall R B. Vibration-based Condition Monitoring: Industrial Aerospace and Automotive Applications[J].Mechanisms&MachineScience, 2010, 3(4):431-477

[3] 孟宗,刘东,岳建辉,等.基于DEMD局部时频熵和SVM的风电齿轮箱故障诊断方法研究[J]. 计量学报，2017，38(4): 449-452.

[4] 袁静, 何正嘉, 訾艳阳. 基于提升多小波的机电设备复合故障分离和提取[J]. 机械工程学报， 2010, 46(1):79-85.

[5] 雷亚国. 基于改进Hilbert-Huang 变换的机械故障诊断[J]. 机械工程学报, 2011, 47(5):71-77.

[6] McNamara B, Wiesenfield K. Theory of stochastic resonance[J].PhysicalReviewA, 1989, 39(9):4854-4869.

[7] Dykman M I, Mannella R, Mcclintock P V，etal. Fluctuation-induced transitions between periodic attractions: observation narrow spetral peaks near a kinetic phase trasition[J].PhysicalReviewLetters, 1990, 65(1):48-51.

[8] Fauve S, Heslot E. Stochastic resonance in a bistable system[J].PhysicalReviewLetters, 1983, 97(1):5-7.

[9] McNamara B, Wiesenfield K, Roy R. Observation of stochastic resonance in a ring laser[J].PhysicalReviewLetters, 1988, 60(25):2626-2629.

[10] Gammaitoni L, Marchesoni F,Menichellasaetta E,etal. Multiplicative stochastic resonance[J].PhysicalReviewLetters, 1989, 62(4):349-352.

[11] Barzykin A V, Seki K. Stochastic resonance drivrn by Gaussian multiplicative noise[J].Epl, 1997, 40(2):117-121.

[12] Mankin R, Ainsaar A,Haljas A,etal. Trichotomous-noise-induced catastrophic shifts in symbiotic ecosystems[J].PhysRevE,2002, 65(5Pt1): 051108.1-051108.9.

[13] Mankin R, Soika E, Sauga A. Multiple noise-enhanced stability versus temperature in asymmertric bistable potential[J].Dynamics,2008, 16(21):239-250.

[14] Soika E, Mankin R. Response of a fractional oscillator to multiplicative trichotomous noise[J].WseasTransactionsonBiology&Biomedicine,2010 ,7(1):21-30.

[15] 李继猛,张云刚,张金凤，等. 基于自适应随机共振的齿轮微弱冲击故障信号增强提取方法研究[J]. 计量学报，2017，38(5): 602-606.

[16] Gandhimathi V M, Rajasekar S, Kurths J. Vibrational and stochastic resonances in two coupled overdamped anharmonic oscillators[J].PhysLettA,2006, 360(2):279-286.

[17] Makra P, Gingl Z. Signal-to noise ratio gain in non-dynamical and dynamical bistable stochastic resonators[J].FluctuationandNoiseLetters, 2002, 2(3):145-153.

[18] Heneghan C, Chow C C, Collins J J,etal. Information measures quanifying aperiodic stochastic resonance[J].PhysRewE, 1996, 54(3):R2228-R2231.