零差干涉仪用于振动校准中关键技术的研究

胡红波, 杨丽峰, 于 梅(中国计量科学研究院, 北京 100029)

1 引 言

加速度计特别是压电加速度计在机械振动冲击、状态监测和故障诊断等工程技术领域广泛应用,加速度计在使用之前必须经过校准,以便确定其输入与输出之间的关系。目前校准加速度计,主要采用的是正弦振动与冲击激励的校准方式,相关ISO标准确定了校准所采用的设备以及校准方法等[1～3]。中国计量科学研究院建立的绝对法振动与冲击加速度基标准装置能够在很宽的频率范围与较高冲击加速度峰值条件下对加速度计进行精确校准[4,5]。

基于两路正交输出的零差激光干涉仪精度高、稳定可靠,且相对成本较低,是实现基于正弦逼近法的绝对法振动校准的主要测量设备[6],因此分辨率不再是问题。零差干涉仪用于低频振动校准时,低频振动位移较大[7],但由于较大的振动速度会引起干涉信号较大频移,故需要较高的采样率来采集两路干涉信号,加上低频周期较长,多周期的采样往往会造成低频测量时数据量过大等问题,从而限制了低频振动校准的下限。本文参考文献[8,9],针对零差干涉仪低频振动测量数据量过大造成干涉信号相位展开和计算正弦参数时的问题做了初步的分析,采用了一种所谓的动态相位展开算法,降低低频振动时对干涉信号的采样率,同时采用递推的算法实现正弦参数的确定,试验表明,本文所述的方法能够有效地降低低频测量时数据量,拓宽零差干涉仪用于低频段校准的工作频率下限。

2 零差干涉仪正交输出信号的特性

零差干涉仪用于绝对法振动校准,主要有3个关键的算法:第1个是两路正交信号的正交误差修正[10];第2个是相位展开;第3个是如何从含有噪声的位移时间序列中估计出幅度与相位。本文主要针对后面两个问题进行分析。假设振动台振动的位移为:

s(t)=s0cos (ω0t+φ0)

(1)

式中:s0为振动位移幅值;ω0=2 p f0为振动的角频率;φ0为相位。则经过修正后的一路零差干涉信号输出如式(2)所示。

(2)

式中:λ为激光波长;L为零差干涉仪测量光与参考光光程差,两者均为常数。利用欧拉公式将式(2)改写成指数形式:

(3)

式(3)中,等式右边两项的第1个乘积部分为常数,第2个乘积部分为雅克比-安格尔恒等式在调频信号处理中的形式。由参考文献[11]可知:

(4)

式中:Jn为第一类贝塞尔函数。

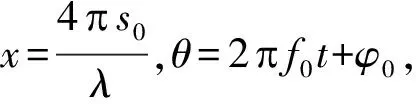
(5)

对式(5)进一步简化,可得:

(6)

对式(6)进行傅里叶变换可得干涉信号对应的频域表达式为:

exp(jnφ0)δ(f-nf0)

(7)

式中:δ(t)为狄拉克函数。

从式(7)中可以看出,零差干涉仪输出信号的傅里叶变换中只包含振动台振动频率f0及其谐波成分。为了便于说明,假定振动台工作的频率f0=1 000Hz,加速度a0=100m/s2,此时理想的一路零差干涉信号及其傅里叶变换如图1所示。

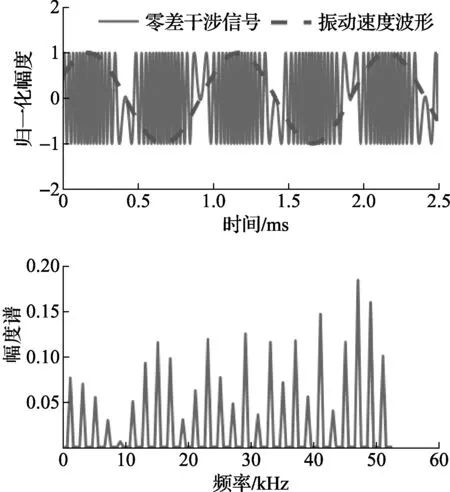
图1 设定振动条件下的零差干涉信号及对应的幅度谱

从图1可以看出,零差干涉信号的最高频率成分约为51kHz,并且其包含的频率成分均为振动频率的高次谐波。另外,依据振动台振动对应的速度vmax,零差干涉信号最高的频率成分fmax=vmax×3.16MHz,也可计算出干涉信号最高频率约为51kHz。

3 动态相位展开的算法

当振动台工作频率为10 Hz时,假定振动加速度为10 m/s2,此时对应的振动速度量约为0.16 m/s,则零差干涉仪输出的两路正交干涉信号最高频率成分为500 kHz,依据采样定理则采样率至少需超过1 MHz才能保证信息不会丢失,为了保证采样周期为10个振动周期,则采样点数至少为106。通常实际测试过中,采样率往往会大于奈奎斯特采样频率,即点数会更多。随着振动频率的降低,振动台运动位移加大,振动速度量往往会更大,加上采样持续时间相对会更长,从而采用点数会急剧增加,最终容易造成解算程序崩溃。作者在将零差干涉仪用于低频振动测量时,采用了一种新的动态相位展开算法,能够有效地降低低频时的采样率,从而降低低频振动测量时所需采集的点数,有效地拓宽了零差干涉仪用于低频振动校准的频率下限。该方法主要是利用了振动速度量是一个连续变化的过程,或者说不能突变的性质,同时利用了相同时刻的加速度量。

设采集到的两路正交零差干涉信号分别为Ux(k)与Uy(k),k=0,1,…,N-1,按式(8)计算相位φ(k):

(8)

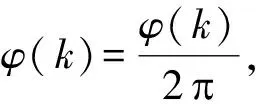
(9)

式中:mk为待确定的整数。假定m0,m1已知,则可以计算2个初始时间的位移量s(0)与s(1),由式(10)可得从时刻0到时刻1的平均速度。

(10)

式中：Δt为采样间隔。按式(11)可计算从时刻1到时刻2时的速度估计值。

v1→2=v0→1+a1×Δt

(11)

式中：a1为时刻1的加速度量,这个量可以通过同步采样被校准的加速度计的输出得到。考虑到日常校准过程中,往往对被校准的加速度计的灵敏度有一定的先验了解,能够大概地估计出被校加速度计的灵敏度,或者可以在参考点的频率下预先校准,也能得到较为可靠的同时刻加速度量的值。在得到了时刻2时的速度量后,可按式(12)得到时刻2的位移的估计值和对应的相移估计值。

(12)

式中：fractuum(x)=x-round(x),round函数值取离x最近的整数。由式(8)可知时刻2真实的相移值φ(2),于是可以得到相移估计值的误差为:

(13)

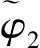
(14)

利用式(12)计算得到的时刻2的位移估计值,最终得到时刻2的位移为:

(15)

至此时刻2的位移量就已经确定了,依次即可确定后续值采样点数N点的位移量。上述算法利用到了相同时刻的加速度量,由于算法利用了的相关振动机械量信息,故未采用由于数据量过大会引起程序无法执行的常规相位展开算法。

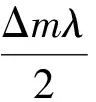
采用这种算法计算的目的主要是为了降低采样率,能够采用的最低的采样率与式(11)有关,即加速度量值的准确与否。假定加速度量估计的误差为ae,则位移估计量的偏差为:

(16)

(17)

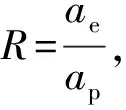
(18)

当振动台工作频率为10 Hz时,假定振动加速度量为10 m/s2,采样率至少需要1 MHz以上,而采用该算法,假设加速度计灵敏度估计误差为0.1,则采样率只需1.78 kHz,不到2 kHz,这样会极大地减小数据量,从而避免由于数据量过大造成后续处理程序的崩溃。

4 幅度和相位角参数确定的递归算法

基于前面解算得到位移信号s(k),标准推荐采用基于最小二乘法的正弦拟合方法。即计算式(19)中参数A,B,C的值。

s(k)=Acosωk-Bsinωk+C

(19)

由于利用最小二乘算法计算参数时需首先利用得到的数据构造数据矩阵,同时在参数计算的过程中还需用到矩阵求逆等运算,当采集得到的数据量较大的时候,矩阵相乘和求逆的运算量急剧增加,会给软件的计算速度和存储量带来很大的负担,并且极易造成软件环境的崩溃。在低频振动校准的时候,由于运动周期较长,不可避免的采样持续时间也较长,故数据量往往会较大,难以采用标准推荐的一次实现算法计算得到参数的值。实际上这个问题是属于参数辨识或者是曲线拟合的问题,在相关的学科中有很多算法可以解决这一问题。结合标准中推荐的计算方法,可以采用最小二乘递推的算法来解决这一问题。递推算法不但能够减少计算量和存储量的问题,还可以实现在线的辨识,也能够跟踪参数的变化。即参数当前时刻的估计值由前一时刻的估计值加上一定的修正量构成,其中修正项一般与残差有关。加权递推计算参数估计值为:

(20)

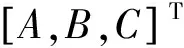
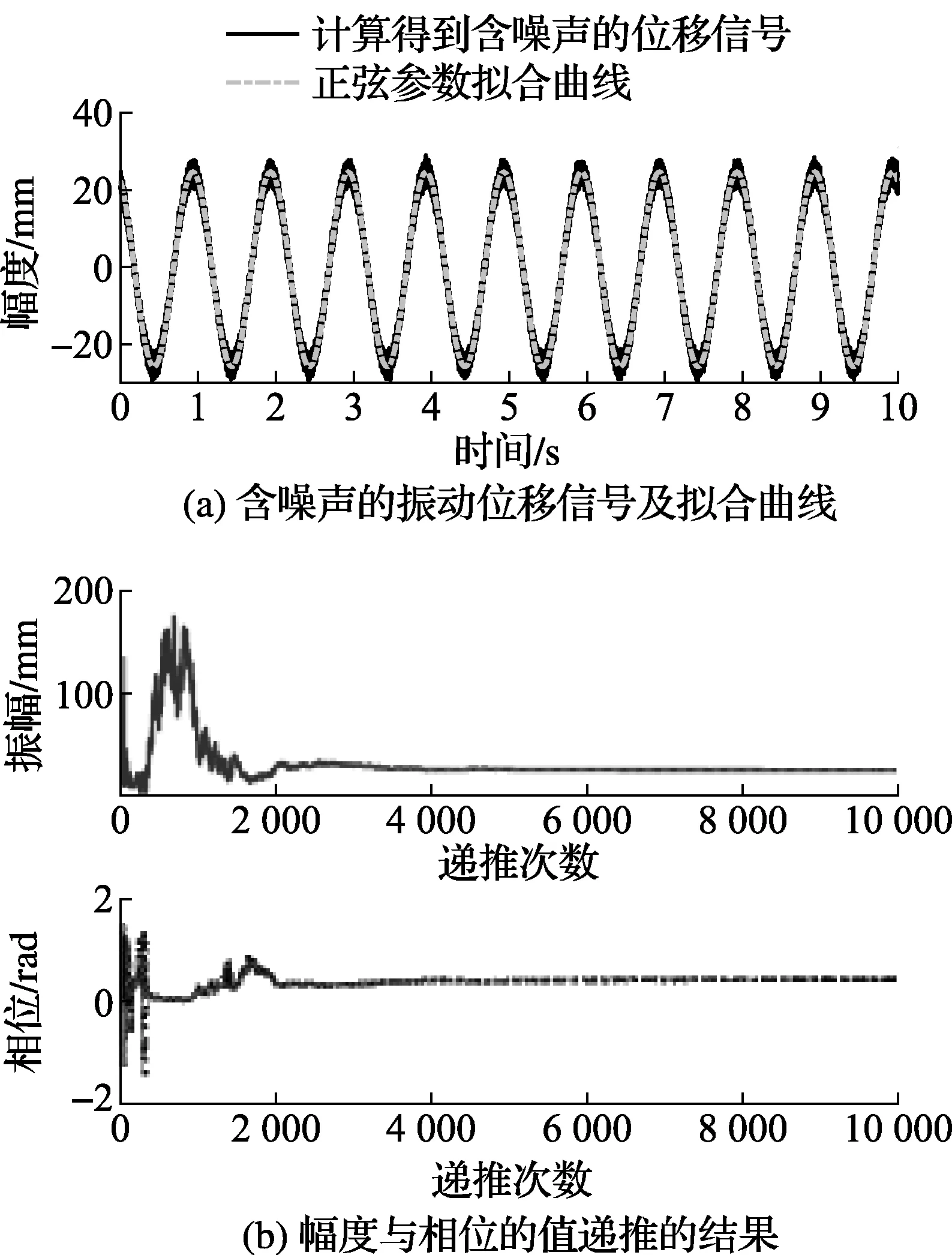
图2 位移信号的拟合与参数值递推计算结果

从图2可以看出,正弦拟合的曲线较好地复现了含噪声的振动位移,同时从振动的振幅与相位参数的递推结果可以看出,大约经过4 000步的递推后,2个参数的值基本稳定,远远小于实际采样得到的点数。另外,在实际测试中可根据要求确定算法停止参数递推的准则。

5 小 结

本文分析了零差干涉仪用于振动测量时两路干涉信号的特点。同时详细说明了在低频振动测量时运用零差干涉仪的主要问题,即由于干涉信号频率成分高,同时低频采样周期长,导致数据量会急剧增加而影响计算程序后续计算的问题。针对此问题,文中详细地说明了一种动态相位展开的算法,该算法利用了振动过程中加速度量的信息,同时利用振动速度量运动的规律,实现了在较低采样率下计算出振动位移量。在计算出振动位移量后,针对计算正弦运动参数计算的问题,采用了一种以最小二乘算法为基础的递推的计算方法,能够有效地避免过多数据组成矩阵运算造成参数无法计算的问题。综上所述,采用本文所述的方法能够有效地降低低频振动时所需要的数据量,拓宽零差干涉仪用于低频振动校准的频率下限,但其校准结果的评估有待进一步分析。

[参考文献]

[1] ISO 1999 International Standard 16063-11 Methods for the calibration of vibration and shock transducers—Part 11: Primary vibration calibration by laser interferometry [S].1999.

[2] ISO 2001 International Standard 16063-13 Methods for the calibration of vibration and shock transducers—Part 13: Primary shock calibration using laser interferometry [S].2001.

[3] 胡红波,孙桥,白杰. 基于窄脉冲冲击激励的压电加速度计动态校准[J]. 计量学报,2017, 38(2):184-188.

[4] 于梅. 0.1 Hz～50 kHz直线振动幅值和相位国家计量基准系统的研究[J]. 振动与冲击,2007,26(7):54-58.

[5] 于梅, 胡红波, 左爱斌,等. 新一代冲击加速度国家计量基准装置的研究与建立[J].振动与冲击,2013,32(10):124-129.

[6] 于梅, 孙桥, 冯源,等. 正弦逼近法振动传感器幅相特性测量技术的研究[J]. 计量学报，2004,25(4):344-348.

[7] SUN Q, Wabniski W, Thomas B. Investigation of primary vibration calibration at high frequencies using the homodyne quadrature sine-approximation method: problems and solutions[J].MeasurementScience&Technology, 2006, 17(8):2197-2205.

[8] Dániel I. Advanced successive phase unwrapping algorithm for quadrature output Michelson interferometers[J].Measurement,2005, 37(2):95-102.

[9] Martens H V. Metrology of vibration measurements by laser techniques[C]// Eighth International Conference on Vibration Measurements by Laser Techniques: Advances and Applications. International Society for Optics and Photonics, 2008:709802-709802-24.

[10] 胡红波,于梅. 零差激光干涉仪正交相位误差的分析[J]. 光电工程,2012,39(12):55-62.

[11] 陈才生. 数学物理方程[M]. 北京:科学出版社,2008.

[12] 方崇智,萧德云. 过程辨识[M]. 北京:清华大学出版社,1988.