改进的K-奇异值分解图像去噪算法
2018-06-22程一峰刘增力昆明理工大学信息工程与自动化学院云南昆明650500
程一峰, 刘增力(昆明理工大学 信息工程与自动化学院, 云南 昆明 650500)
1 引 言
近年来,稀疏表示在图像去噪中的应用越来越广泛,成为前沿研究课题。Mallat等[1]提出超完备字典,基于超完备字典的稀疏表示是图像稀疏去噪的重要研究方向,而字典的设计则是该方向上重要的研究环节。全局字典以及自适应字典是字典的两类重要分支,最近几年,超完备字典通过学习和训练而获得的方法得到很大的进展。Aharon M,Elad M等[2]提出了K-SVD(K-singular value decomposition)算法,达到了良好的去噪效果。然而传统的K-SVD算法在一些方面仍然存在不足,具体表现如下:字典在更新过程中会出现每一列无法全部更新或部分列失效的问题,原因是初始化字典的选择不恰当,最终结果会导致信号利用率低;在噪声比较强的时候,字典中含有与噪声匹配的大量噪声原子,导致字典在学习过程中无法有效地将噪声去除;K-SVD算法运算时间较长,体现在图像训练过程中会占用大量的时间;传统最速下降算法锯齿现象严重。
本文针对传统的K-SVD算法的几点不足,对其进行了改进:首先,通过稀疏贝叶斯学习(sparse Bayesian learning,SBL)[3]对图像进行预处理,提高图像信号的利用率;然后,对字典进行优化,并结合Bartlett检验法[4]将噪声原子裁剪,提高去噪后图像质量;第三,针对运算时间较长的问题,研究凸优化算法中的最速下降法,将改进的最速下降算法与正交匹配追踪(orthogonal matching pursuit,OMP)相结合;第四,将最速下降算法进行一维搜索,有效地抑制了锯齿现象。实验结果表明,通过本文的图像去噪方法,图像精度和峰值信噪比(peak signal to noise ratio,PSNR)值都得到了提高。
2 图像的稀疏表示模型
2.1 K-均值聚类算法
通过K-均值(K-means)聚类算法将图像块进行聚类处理,将具有相似集合形态的图像块聚集在一起,再通过K-SVD算法对每一个相似块训练出各自的优化字典,最终得到的字典更具有针对性。
K-均值聚类算法的主要方法步骤如下:首先从全体n个数据中选择k个聚类中心。根据剩下的n-k个对象与k个聚类中心的相似度,将每个对象分配到k个聚类中心中与其最为相似的聚类中去。如果类中心有变化则对其进行反复聚类计算,直到类中心不再发生变化以及平方误差函数收敛为止。平方误差函数的定义可以表示为[5,6]:
(1)
式中:xji为第j类第i个样本;kj为第j类的均值或称聚类中心;nj为第j类样本个数;E为数据对象及其相应的聚类中心的均方差总和。
2.2 稀疏贝叶斯学习
在K-SVD算法中,字典在更新过程中经常会出现每一列不能全部更新或部分列失效的现象,为了解决这个问题,可以通过贝叶斯学习[7]对信号进行预处理,通过贝叶斯概率模型进行迭代直到信号的稀疏表示。
1) 计算βij的协方差矩阵与βij:
βij协方差矩阵为
(2)
式中:βij为稀疏向量;Γ为k×k阶对角矩阵,γ1,γ2,…,γk为对角元素;D为过完备字典矩阵;σ为噪声标准差。
(3)
式中:Xij为图像子块。
2) 更新噪声:
(4)
式中:Rij为提取子图的矩阵;X为含噪图像块。
(5)

2.3 字典噪声原子裁剪
传统K-SVD的方法在训练含噪图像之后,得到的字典中会出现与噪声匹配的噪声原子,因此对于字典进行优化的关键步骤就是删除这些噪声原子。然而关键问题是:如何对噪声原子进行检测。文献[8]中提出利用假设检验来检测噪声原子。噪声原子采用对角、反对角、水平、垂直4个扫描方向进行对比扫描,更能提高相关性检测的能力。
设μi为特征向量的方差,在噪声原子4个方向上用Bartlett检验法测试特征向量的方差μi是否相等,或者至少有2个原子的方差不等,Bartlett检验统计量H的定义为:
(6)
式中:n为原子元素数量。
对原子库中的原子进行判断,若某个原子满足H<χ2(β;3),则认为该原子为噪声原子,并且进行删除。χ2(β;3)表示自由度为3的卡方分布上的β百分点位置。与通过挖掘原子库的冗余性来减小原子数目的传统字典优化方法对比可以发现,该方法不会对信息原子产生影响,只会从字典中删除噪声原子,从而提高了逼近质量以及去噪效果。
2.4 改进的最速下降正交匹配追踪
传统的最速下降算法虽然拥有很多的优点和可取之处,但是该算法依然存在缺点。在迭代过程中迭代点呈现了相应的“之”字型,此现象为锯齿现象,对收敛速度会产生影响,但是锯齿现象又是无法避免的。因此可以通过抑制锯齿现象从而可以提高收敛速度。
稀疏分解图像的目标是找到一个矩阵α并且满足:
(7)
式中:||α||0为α的非零元个数。
目前,稀疏分解方法可分为基追踪(BP),匹配追踪(MP)和正交匹配追踪(OMP)。OMP是最好的匹配追踪算法并且具有最适用的基础表达功能。式(7)可以转换为无约束最优化问题,即:
(8)
式中:λ为正则化参数。
尽管OMP算法比其他方法快,但其仍以损失一定的精度为代价。考虑到凸优化算法具有较高的精度但收敛速度较慢的特点,本文将改进的最速下降算法与OMP算法相结合,即改进的最速下降OMP。利用改进的最速下降算法去求解式(8)。
通常将式(8)看成是一种多元函数f(x)的无约束优化问题,其寻优表达式为[9,10]:
αk+1=αk+tkpk
(9)
式中:tk为优化迭代的步长;pk为第k次迭代搜索方向。
通常认为在一个点上最快的下降方向是这一点的负梯度方向。于是可以定义:
pk=-f(αk)
(10)
每次优化迭代的步长tk可以通过式(11)求得,即:
(11)
如果tk-1f(X(k+1))Tp(k-1)<0,则转入式(12),否则转入式(14)。
令p′k=X(k)-X′,从X(k)出发,沿着p′k搜索方向进行一维搜索,求出步长t′k,使得
(12)
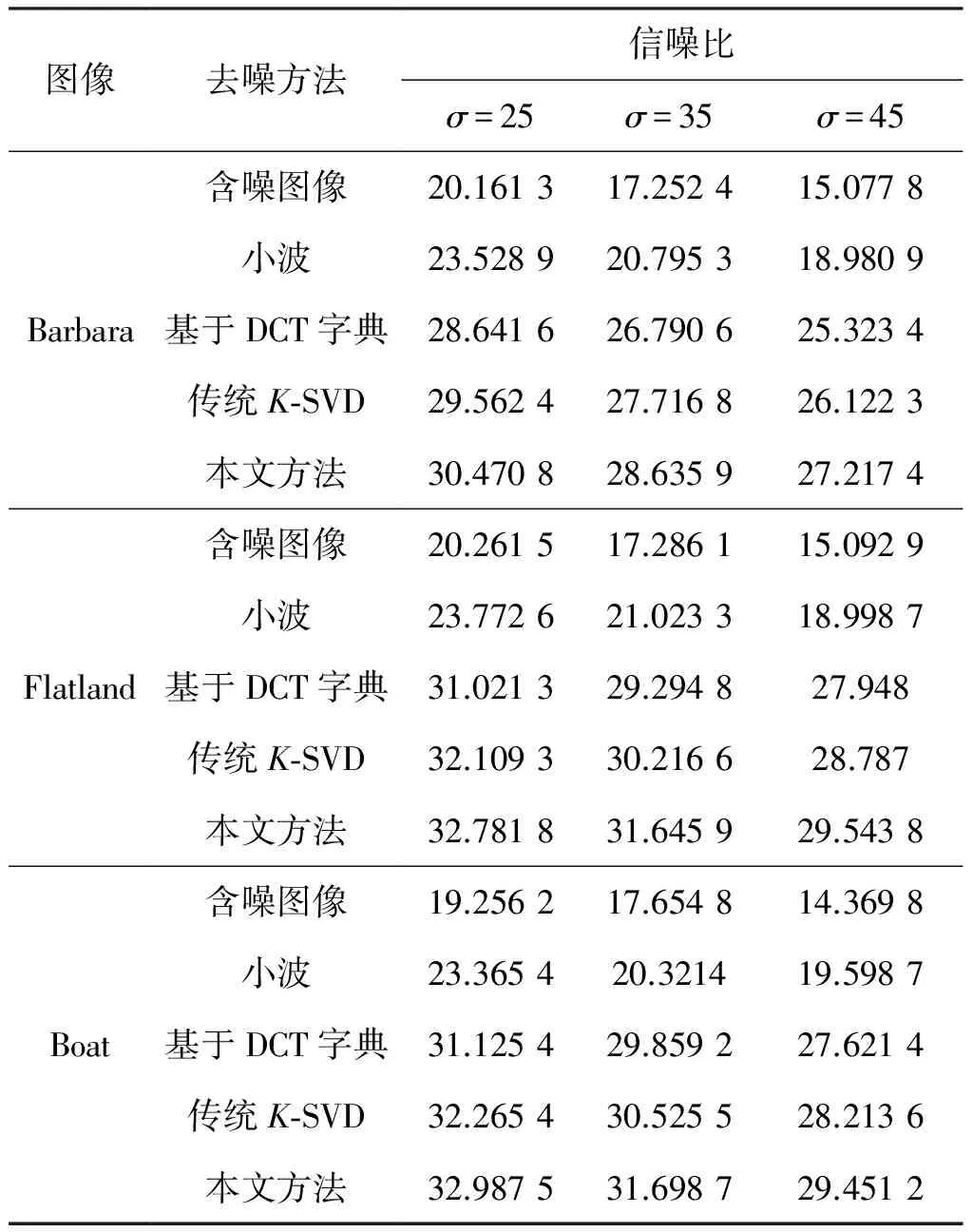
若f(X(k)+t′kp′k) X(k+1)=X(k)+tkpk (13) 置k=k+1,转到式(10)。 该算法通过在p=X(k+1)-X(k-1)方向上进行一维搜索,得到一个比原始算法更好的迭代点。 (14) 式中:G=DTD;b=DTX。 对式(14)求导可得: f(Xk)=Gα-b=-DTr (15) pk=-f(Xk)=DTr (16) 式中:r为残差矩阵。 (17) 结合改进之后的最速下降算法在凸优化算法中的优点及贪婪迭代算法中OMP的优点。改进的最速下降OMP可以概括如下: OMP的分解方法的目的是解决 (18) 步骤1:初始化。残差r0=X,αx是X(X是含噪图像块)的稀疏系数,Dx是X的字典,Dx∈D,ε是误差控制参数,原子下标索引集合I=φ。 步骤2:迭代L次,更新原子下标索引集I=I∪{i}。 1)选择原子i和相应的稀疏系数αx,通过集合I使得目标函数最小化 (19) 2)更新I,I=I∪{i} 3)更新矩阵的最优稀疏系数αx (20) 4)更新残差向量 rk+1=rk-Dxtkpk (21) 步骤3:更新迭代残差,当||rk+1||2<ε停止迭代,其它情况则返回步骤2。 本文利用稀疏贝叶斯学习对含噪图像进行预处理,提高其信号利用率。并且结合改进的最速下降正交匹配追踪以及噪声原子裁剪对字典进行更新。具体算法步骤如下: 步骤1:初始化阶。首先利用K-means聚类算法对大小为N的图像Y进行聚类,将图像分为n类(n≪N),并令有k个超参数的向量为γ=[γ1,γ2,…,γk]T,得到图像子块Xij=RijX,i=1,2,…,k;j=1,2,…,n;Rij为图像子块矩阵。最后,初始化字典D(0)∈Rn×k为过完备DCT基,并令J=1。 步骤2:稀疏贝叶斯学习。当J≤Jmax时,针对每一类图像块Xij用稀疏贝叶斯学习不断更新噪声大小,并且求得稀疏系数向量αij。 (22) 1)定义稀疏系数不为零的图像块集合为ωl={(i,j)|αij(l)≠0}。 步骤5:字典优化。进行噪声监测并删除噪声原子。 步骤6:图像去噪。在去噪过程中存在着图像块的重叠现象,因此应该对图像块的重叠部分做平均,去噪之后的图像的近似解为: 选取PSNR较大的图像作为最终去噪输出图像。 实验是将本文算法与经典图像去噪算法:小波阈值去噪,基于非自适应冗余DCT字典去噪,基于传统K-SVD方法去噪在MATLAB上进行仿真对比。实验结果见图1、图2和图3。 图1 Boat原图与加噪图像 图2 不同字典对比 从仿真结果可以看出,本文方法对于含噪图像去噪效果明显,能够很好地保留图像的边缘纹理信息。与传统去噪方法进行对比之后,可以发现,本文算法的去噪效果优于传统去噪,图像精度提高。 对Barbara,Flatland和Boat 3种图像,选用不同去噪方法的峰值信噪比值比较结果见表1。 图3 不同方法的去噪对比 表1 不同方法的峰值信噪比值比较 dB 通过表1可以发现,不论是稀疏性较好的Barbara图亦或是稀疏性较弱的Flatland和Boat图,利用本文方法,峰值信噪比都明显比其他方法提高不少,相对于传统的K-SVD,本文方法提高了大概1 dB。因此,本文方法相对于其他去噪方法,综合去噪能力显著提高。 首先通过稀疏贝叶斯学习对含噪图像进行预处理, 提高信号利用率。接着将改进之后的OMP算法,以及原子裁剪方法相结合,构成了改进之后的K-SVD算法对图像进行去噪。通过实验分析可以看出,相对于传统去噪算法,本文方法能够更好地提高图像的精度,图像边缘和纹理部分保留完好,峰值信噪比显著提高,并且去噪效率也有所提高。 [参考文献] [1] Mallat S G, ZHANG Z F. Matching pursuit with time-frequency dictionary[J].IEEETransactionsonSignalProcessing, 1993, 41(12):3397-3415. [2] Aharon M, Elad M, Bruckstrein A M. TheK-SVD: an algorithm for designing of over-complete dictionaries for sparse representation[J].IEEETransactiononImageProcessing, 2006, 54(11): 4311-4322. [3] Wipf D P, Rao B D. Sparse Bayesian learning for basisselection[J].SignalProcessingIEEETranson, 2004, 52,(8):2153-2164. [4] Bartlett M S. Properties of Sufficiency and Statistical Tests[J].ProceedingsoftheRoyalSocietyofLondon.SeriesA,MathematicalandPhysicalSciences,1937, 160(901):268-282. [5] 蒋帅.K-均值聚类算法研究[D]. 西安:陕西师范大学, 2010. [6] 田源,王洪涛. 基于量子核聚类算法的图像边缘特征提取研究[J]. 计量学报,2016,37(6):582-586. [7] ZHOU F, LI L. Modified sparse Bayesian dictionary learningK-SVD algorithm for video image sparse representation[J].JournalofComputationalInformationSystems, 2015, 11(12):4567-4580. [8] Lee J, Kim Y H, Nam J H. Adaptive noise reduction algorithms based on statistical hypotheses tests[J].IEEETransactionsonConsumerElectronics, 2008, 54(3):1406-1414. [9] 龙建辉, 胡锡炎, 张磊. 最速下降法解二次矩阵方程[J]. 湖南大学学报(自然科学版), 2008, 54(3):85-88. [10] 郑慧峰,喻桑桑,王月兵,等. 基于经验模态分解和奇异值分解的振动声调制信号分析方法研究[J]. 计量学报,2016,37(4):398-401. [11] 周灿梅. 基于压缩感知的信号重建算法研究[D].北京:北京交通大学, 2010.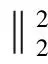
3 改进的K-SVD图像去噪算法

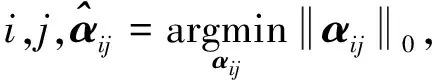




4 实验结果分析



5 结 论
