水平仪测试竖直轴系倾角回转误差的数据处理

王子豪， 任顺清(哈尔滨工业大学 空间控制与惯性技术研究中心， 哈尔滨， 黑龙江 150080)

1 引 言

倾角回转误差是精密仪器的关键技术指标，轴系回转精度可以提高惯性仪表的测试精度，改进工件的检测精度，提高机床上零件的加工精度。文献[1～3]介绍了多自由度模型并分析了主轴轴承的加工误差，包括标准圆柱与轴的同心度误差，并提出转台误差检测及分离的快捷方法;文献[4～6]设计和验证主轴运动误差分离技术具有亚纳米测量不确定度，利用误差分离技术提高圆度仪测试的精度;文献[7，8]针对数控机床，提出了基于混沌相空间重构理论的运动精度演化分析方法;文献[9，10]介绍了在主轴回转误差测试过程中，如何消除标准圆柱的安装偏心误差,实现了对高精度静压主轴回转误差和圆度的精确测量;文献[11～13]分别采用光电检测、反向法、小波变换等方法对回转误差进行测试，但没有考虑轴系的一次谐振运动对轴系倾角回转误差的影响;文献[14]的直接消偏法消除了回转误差中的部分二次谐波项，也消除了回转误差中的部分一次谐振项;文献[15]在精密计算竖直回转轴线对水平面的铅垂度后，加以消除，再扣除常数项，计算合成误差时，有一次谐振没有分离，产生一定的耦合。本文针对水平仪测量竖直轴系的回转误差的数据处理问题，基于文献[15]，将铅垂度误差消除后进行坐标转换，使得轴系回转误差的二次及以上谐波完全分离出来，使原来的台面对轴线的垂直度误差转换为正交的一次谐波，分离出正交的一次谐波和轴系二维同相的一次谐振，解决了水平仪测量竖直轴系回转误差中的安装误差与回转误差的分离问题，可更准确地测试与评估轴系的倾角回转误差。

2 水平仪测试轴系倾角回转误差的4种数据处理方法

2.1 测试数据中误差的组成成份分析

由文献[14]可得水平仪读数的表达式为

fx(γ) =-Δαy2-[Δθy0+Δθy1(γ)] cosγ+

[Δθx0+Δθx1(γ)] sinγ

(1)

fy(γ) =Δαx2+[Δθy0+Δθy1(γ)] sinγ+

[Δθx0+Δθx1(γ)] cosγ

(2)

式中：fx(γ)和fy(γ)分别为x和y方向水平仪读数，一周内等间隔取点;γ=(2p i)/n,n为取点个数，i=0,1,2,…,n-1；Δθx0、Δθy0为主轴轴线对水平面的垂直度(也称铅垂度)；Δαx2和Δαy2为水平仪安装平面相对主轴轴线的垂直度；Δθx1(γ)和Δθy1(γ)为主轴旋转到γ角位置时的倾角回转误差， 可视为以2p 为周期的周期函数，Δθx1(γ)和Δθy1(γ)可展开成Fourier级数：

(3)

(4)

式中：Δθx1(γ)中第j次谐波余弦、正弦项幅值为Acj、Asj；Δθy1(γ)中第j次谐波余弦、正弦项幅值为Bcj、Bsj。根据文献[16]，认为轴系回转误差中的一次谐波主要由一次谐振引起，即Ac1∶As1=Bc1∶Bs1，是轴系回转时结构和元件的振动或不等刚度等引起的。

利用三角函数和差化积方法，将Fourier级数展开后的倾角回转误差式(3)、(4)代入式(1)、(2)，化简之后得到测试数据的谐波成分，对测试数据的谐波成分与回转误差的谐波成分进行分析比对，见表1。从表1可以看出水平仪读数一次谐波中包含Fourier级数展开后的倾角回转误差二次谐波项Ac2、As2、Bc2、Bs2，水平仪读数二次谐波中包含倾角回转误差一次谐波项Ac1、As1、Bc1、Bs1和倾角回转误差一次谐波项Ac3、As3、Bc3、Bs3，由此可证明水平仪测试数据中的谐波成分与回转误差中的谐波成分是不相同的。

表1 测试数据与回转误差的谐波成份比对

回转误差的评定，包括各次谐波成分，都是相对于轴套坐标系的，所以固定坐标系下的回转误差中的一次谐波经过坐标转换到运动的轴坐标系中，则表现为常数项和二次谐波项，其轴系回转误差中的一次谐波在二维测试数据中则也表现为常数项和二次谐波项：

x方向：-0.5Bc1+0.5As1， -0.5(Bc1+As1) cos 2γ+0.5(Ac1-Bs1) sin 2γ；

y方向： 0.5Bs1+0.5Ac1， 0.5(Bc1+As1) sin 2γ+0.5(Ac1-Bs1) cos 2γ。

回转误差二次谐波项在二维测试数据中表现为一次谐波和三次谐波项：

0.5(As2-Bc2) cosγ-0.5(Ac2+Bs2) sinγ， -0.5(Bc2+As2) cos 3γ+0.5(Ac2-Bs2) sin 3γ；

0.5(As2-Bc2) sinγ+0.5(Ac2+Bs2) cosγ， 0.5(Bc2+As2) sin 3γ+0.5(Ac2-Bs2) cos 3γ。

依此类推，回转误差的j次谐波在测试数据中表现为j-1次谐波与j+1次谐波的合成，若将铅垂度误差、台面对轴线的垂直度误差消除，是不能直接从测试数据中消除一次谐波和常数项的。针对式(1)、(2)，本文将对已有的两种数据处理方法[14,15]进行深入分析，并提出两种新的数据处理方法，目的是彻底分离出式(1)、(2)中的各项误差。

2.2 4种数据处理方法

2.2.1 直接消偏法

第1种方法是直接消偏法[14]。是从式(1)、(2)中直接扣除一次谐波和常数项，处理方法为：

(5)

(6)

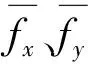
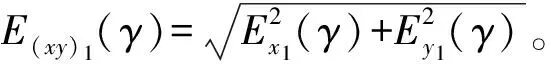
2.2.2 间接消偏法

第2种方法是间接消偏法[15]。可以先根据式(7)和式(8)精确地将铅垂度误差Δθx0和Δθy0分离出来:

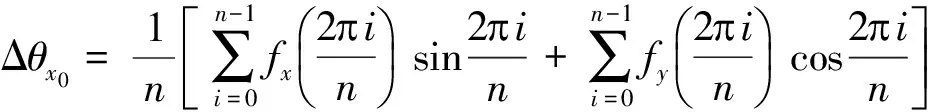
(7)

(8)

接着将主轴铅垂度误差Δθx0和Δθy0从式(1)、(2)中消除后，再将平均值从水平仪测试数据中的剔除，即：

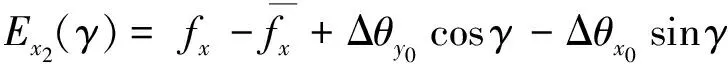
(9)

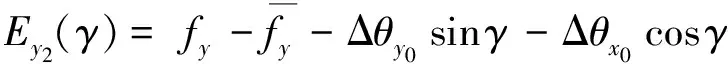
(10)

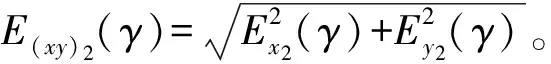
2.2.3 转换坐标系后的消偏法

转换坐标后的消偏方法,是将铅垂度从测量数据fx(γ)、fy(γ)中消除，再转换到固定坐标系下消偏，即：

f(γ) =fx(γ)+Δθy0cosγ-Δθx0sinγ

=-Δαy2-Δθy1(γ) cosγ+Δθx1(γ) sinγ

(11)

g(γ) =fy(γ)-Δθy0sinγ-Δθx0cosγ

=Δαx2+Δθy1(γ) sinγ+Δθx1(γ) cosγ

(12)

再将式(11)、(12)转换到固定坐标系下，

wx(γ) =-f(γ) cosγ+g(γ) sinγ

=Δαy2cosγ+Δαx2sinγ+Δθy1(γ)

(13)

wy(γ) =f(γ) sinγ+g(γ) cosγ

=-Δαy2sinγ+Δαx2cosγ+Δθx1(γ)

(14)

式(13)、(14)中一次谐波系数为

消除一次谐波后,

Ex3(γ)=wx(γ)-Δθx1c3cosγ-Δθx1s3sinγ

(15)

Ey3(γ)=wy(γ)-Δθy1c3cosγ-Δθy1s3sinγ

(16)

2.2.4 转换坐标系后的一次谐波分离法

从式(13)、(14)可以看出台面对轴线的垂直度Δαx2和Δαy2在水平仪的读数中表现为常数项，在wx(γ)、wy(γ)中产生的一次谐波是相位正交的，幅值是相等的，而与回转误差Δθx1(γ)、Δθy1(γ)中一次谐波为As1、Ac1、Bs1、Bc1，其一次谐振分别为Bc1cosγ+Bs1sinγ、Ac1cosγ+As1sinγ且满足As1Bc1=Ac1Bs1，即两个方向的一次谐振相关的，即完全相关的一次谐振，因此Δαx2、Δαy2产生的一次谐波与回转误差中的一次谐波的分离是可以实现的。

假设回转误差中一次谐振运动的参数方程表示为

lx(γ)=(excosγ+eysinγ) cosλ

(17)

ly(γ)=(excosγ+eysinγ) sinλ

(18)

式中ex、ey将在下面的推导式(21,22)中给出。

将式(13)、(14)中的一次谐波写成:

gx(γ)=(Δαy2+excosλ) cosγ+(Δαx2+

eycosλ) sinγ=Δθx1c4cosγ+Δθx1s4sinγ

(19)

gy(γ)=(-Δαy2+eysinλ) sinγ+(Δαx2+

exsinλ) cosγ=Δθy1c4cosγ+Δθy1s4sinγ

(20)

相关的一次谐振与正交的一次谐波叠加为gx1(γ)、gy1(γ)所形成Lissajous图为一椭圆，轴系一次谐振运动的分解如图1所示。而一次谐振的方向为椭圆的长轴方向，即MN方向，点M、N到原点O的距离最大。

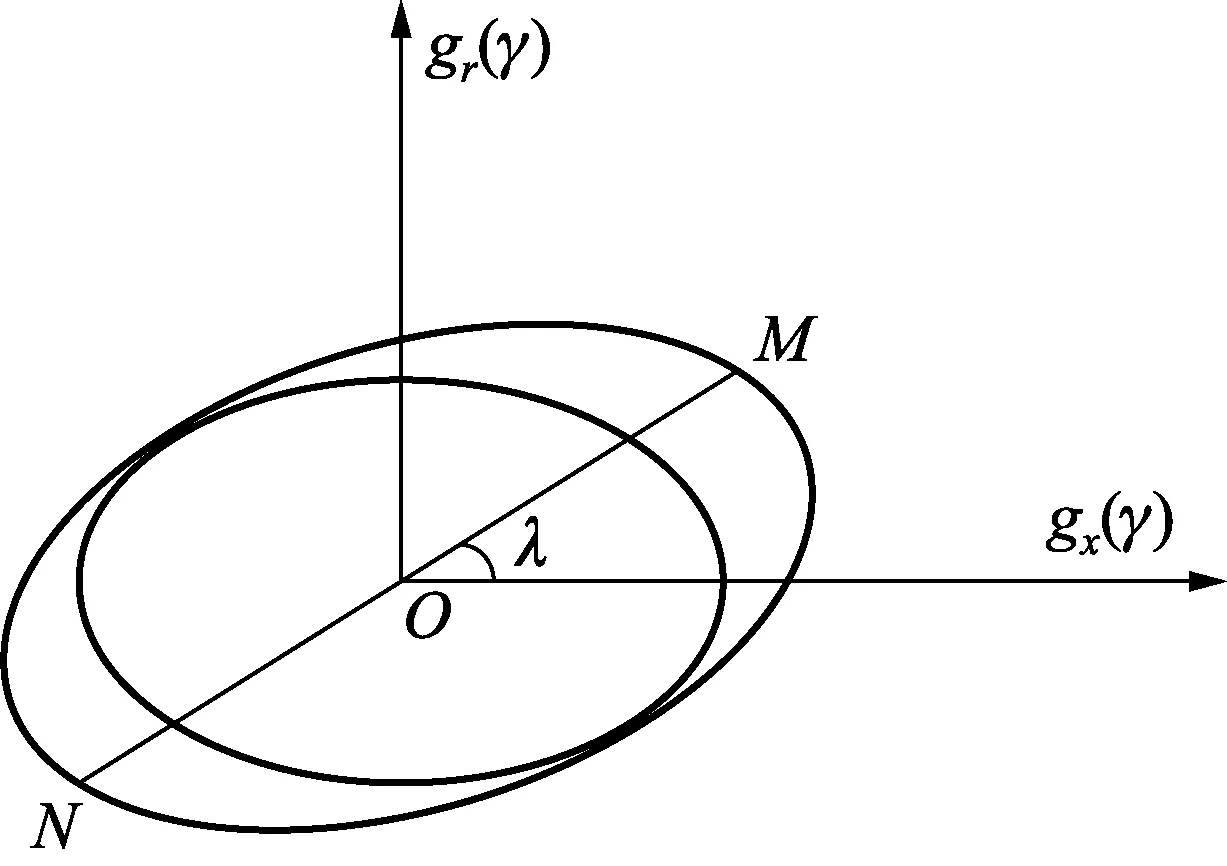
图1 轴系一次谐振运动的分解

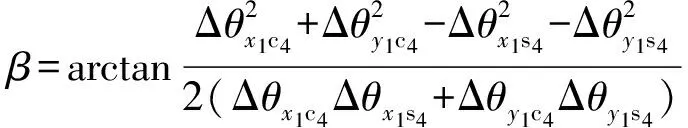
经过详细推导与计算，得

ex=(Δθy1c4-Δθx1s4) sinλ+(Δθx1c4+Δθy1s4) cosλ

(21)

ey=(Δθx1c4+Δθy1s4) sinλ+(Δθx1s4-Δθy1c4) cosλ

(22)

Δαy2=Δθx1c4-excosλ=-(Δθy1s4-eysinλ)

=(1- cos2λ)Δθx1c4+Δθy1s4cos2λ-

(Δθy1c4+Δθx1s4) sinλcosλ

(23)

Δαx2=Δθx1s4-eycosλ=Δθy1c4-exsinλ

=(1- cos2λ)Δθx1s4+Δθy1c4cos2λ-

(-Δθx1c4+Δθy1s4) sinλcosλ

(24)

剔除水平仪平面的安装误差Δαx2、Δαy2，最后回转误差数据处理为

Ex4(γ)=gx(γ)-Δαy2cosγ-Δαx2sinγ

(25)

Ey4(γ)=gy(γ)+Δαy2sinγ-Δαx2cosγ

(26)

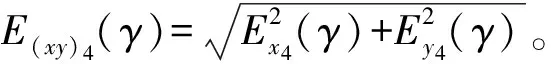
3 4种数据处理方法分析及比较

(1) 采用直接消偏法，将表1数据代入式(5)、(6)可得：

Ex1(γ) =-0.5Bc1cos 2γ-0.5Bs1sin 2γ+0.5Ac1sin 2γ-

0.5As1cos 2γ-0.5Bc2cos 3γ-0.5Bs2sin 3γ+

0.5Ac2sin 3γ-0.5As2cos 3γ-0.5Bc3cos 4γ-

0.5Bs3sin 2γ-0.5Bs3sin 4γ-0.5Bs3sin 2γ+

0.5Ac3sin 4γ-0.5Ac3sin 2γ+0.5As3cos 2γ-

0.5As3cos 4γ+…

(27)

Ey1(γ) =0.5Bc1sin 2γ-0.5Bs1cos 2γ+0.5Ac1cos 2γ+

0.5As1sin 2γ+0.5Bc2sin 3γ-0.5Bs2cos 3γ+

0.5Ac2cos 3γ+0.5As2sin 3γ+0.5Bc3sin 4γ-

0.5Bs3sin 2γ+0.5Bs3cos 2γ-0.5Bs3cos 4γ+

0.5Ac3cos 4γ+0.5Ac3cos 2γ+0.5As3sin 2γ-

0.5As3sin 2γ+…

(28)

从Ex1(γ)、Ey1(γ)中可以看出，回转误差中的3，4，…次谐波成分得以保留，而回转误差中的二次谐波及一次谐振量只能部分保留，如果Ac1=Bs1、Bc1=-As1，则回转误差中不能反映出一次谐振量。当Bc2=-As2、Ac2=Bs2时，则Ex1(γ)、Ey1(γ)中完全不反映回转误差中的二次谐波，然而回转误差的二次谐波往往是其主要成分。

(2) 采用间接消偏法，将式(13)、(14)代入式(15)和式(16)得：

Ex2(γ) =-0.5Bc1cos 2γ-0.5Bs1sin 2γ+0.5Ac1sin 2γ-

0.5As1cos 2γ+0.5Ac2sin 3γ-0.5Ac2sinγ+

0.5As2cosγ-0.5As2cos 3γ-0.5Bc2cos 3γ-

0.5Bc2cosγ-0.5Bs2sin 3γ-0.5Bs2sinγ+…

(29)

Ey2(γ) =0.5Bc1sin 2γ-0.5Bs1cos 2γ+0.5Ac1cos 2γ+

0.5As1sin 2γ+0.5Ac2cos 3γ+0.5Ac2cosγ+

0.5As2sin 3γ+0.5As2sinγ+0.5Bc2sin 3γ-

0.5Bc2sinγ+0.5Bs2cosγ-0.5Bs2cos 3γ+…

(30)

从Ex2(γ)、Ey2(γ)中可以看出，它们保留了回转误差2，3，4，…次谐波。当极端情况Ac1=Bs1或Bc1=-As1出现时，一次谐振部分消失，而回转误差中的二次及以上谐波成分均反映出来，但回转误差是在动坐标系下表示的，Ex2(γ)、Ey2(γ)中不反映轴系的一次谐振量，所以这种方法只能反映出部分一次谐振量。

(3) 采用转换坐标系后的消偏法，从式(13)、(14)可以看出，这种方法最大的优点是将轴系回转误差转换到了静坐标系下，大大减少了轴系回转误差与Δθx0、Δθy0和Δαx2、Δαy2之间的相互耦合，而前两种方法轴系回转误差是在动坐标系下表示的，水平仪测试数据中的谐波成分与回转误差中的谐波成分是不一样的，误差角之间耦合现象较为严重。

wx(γ)、wy(γ)中一次谐波系数代入式(15)和式(16)得：

Ex3(γ) =Δθy1(γ)-Bc1cosγ-Bs1sinγ

=Bc2cos 2γ+Bs2sin 2γ+…

(31)

Ey3(γ) =Δθx1(γ)-Ac1cosγ-As1sinγ

=Ac2cos 2γ+As2sin 2γ+…

(32)

文中的消偏包括剔除铅垂度和剔除台面对轴线的垂直度(包括水平仪零位误差)。将铅垂度剔除的条件是两维水平仪测试数据经坐标系转换，铅垂度不与其他误差耦合。从理论上可以完全剔除铅垂度，但安装面与轴线垂直度以及水平仪自身的零位则又要经过一次转换进行消偏。虽然转换坐标系后的消偏，大大减少了误差角之间耦合，但是直接剔除一次谐波项，则回转误差中的一次谐振项也随之剔除了，处理的结果仅含有回转误差中的2次及2次以上谐波成分，但是却完全不包含回转误差中的一次谐波。

(4)采用转换坐标系后的一次谐波分离法，由于Δαx2和Δαy2成功分离出来，在式(13)、(14)的基础上剔除，得:

Ex4(γ) =gx(γ)-Δαy2cosγ-Δαx2sinγ=

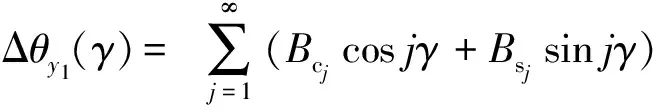
(33)

Ey4(γ) =gy(γ)+Δαy2sinγ-Δαx2cosγ

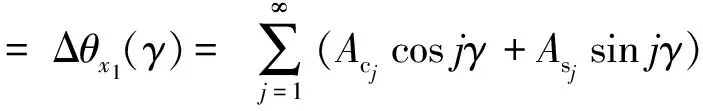
(34)

处理结果包含了回转误差中的所有谐波成分，而且是在动坐标系下表示较为完善的数据处理方法。下面将以实验测试数据对4种方法进行对比，验证第4种方法转换坐标系后的一次谐波分离法的正确性。

4 测试实例分析

利用2台高精度水平仪对某轴系倾角回转误差进行二维测试。在改变了主轴的垂直度误差的情况下进行8次实验，结果如表2所示。

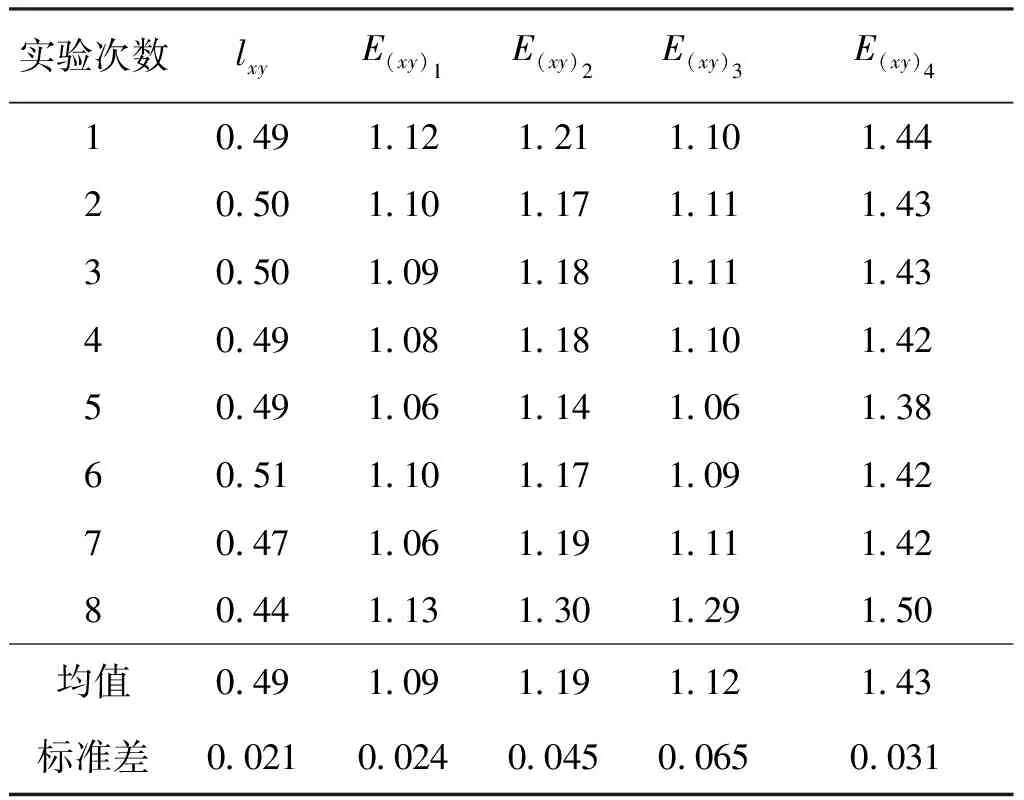
表2 不同主轴垂直度误差下的倾角回转误差 (″)

从表2中可以看出，在8次实验中直接消偏法计算的回转误差均值为1.09″，虽然算出的回转误差最小，但回转误差中的二次谐波及一次谐振量只能部分保留；间接消偏法为1.19″，转换坐标系后的消偏法为1.12″，这是由于前者只能将回转误差中一次谐振量部分保留，而后者将一次谐振量全部剔除了，所以间接验证了推导的正确性。转换坐标系后的一次谐波分离法计算的回转误差的结果最大，为1.43″，它将回转误差所有谐波成分完整的保留下来，包括完整的一次谐振。实验次数2～8是在改变了主轴的垂直度误差的情况下进行的，8次实验回转误差参数进行比较，见表3。

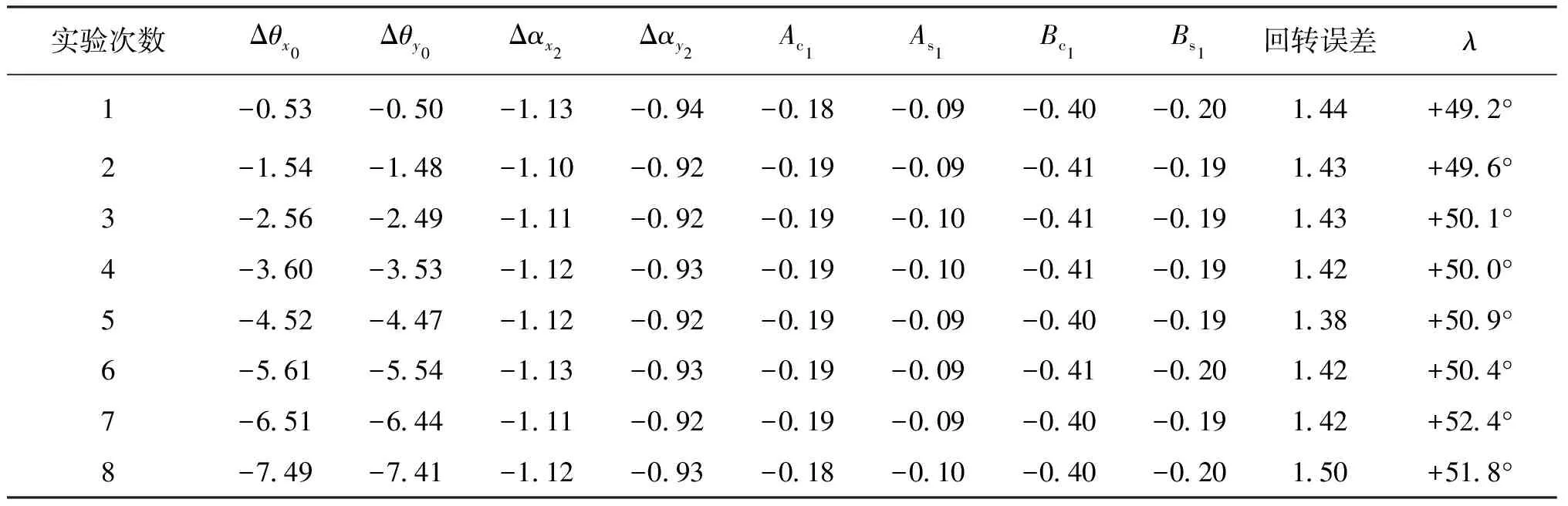
表3 8次实验回转误差参数对比 (＂)

从表3中可以看到8次实验在改变主轴的垂直度误差之后，主轴偏差Δθx0和Δθy0形成的圆周半径是不一样的，安装平面对于主轴轴线的垂直度Δαx2和Δαy2基本不发生改变，8次实验中一次谐振运动摆幅lxy均值为-0.49″～+0.49″，一次谐振直线方位角λ在+49.2°～+52.4°范围内，均值为+50.6°，标准差为+1.0°，可认为一次谐振运动的方位角基本相同，轴系的一次谐振运动具有较高的重复性。采用改进后的数据处理算法，分离出的回转误差标准差仅相差0.031″，同时回转误差其一次谐波的系数也几乎完全相同，进一步验证了本文所给出的改进方法的正确性。而实验中一次谐振运动所占整体轴系倾角回转误差约为35%，也说明了对于回转精度高的轴系，其一次谐振运动是不能被忽略的，在对轴系回转误差的评定过程中应加以考虑。

5 结 论

通过分析回转误差中的谐波成分与水平仪测试数据中的谐波成分的关系，在现有两种数据处理方法的基础上提出了新的2种数据处理方法，通过分析对比，得出如下结论：

(1)回转误差的j次谐波在测试数据中表现为j-1 次谐波与j+1次谐波的合成，若将铅垂度误差、台面对轴线的垂直度误差剔除，是不能直接从测试数据中消除一次谐波和常数项的。

(2)直接消偏法只保留了回转误差中部分一次谐振与二次谐波，极限情况不能反映一次谐振和二次谐波，因此算出的回转误差值最小但不够准确。间接消偏法出现了坐标转换问题，同时只能反映部分一次谐振误差，极限情况不能反映一次谐振误差。而转换坐标系后的消偏方法因为台面对轴线的垂直度转换到静坐标下为正交的一次谐波，且与回转误差中相关的一次谐波相混叠，直接剔除一次谐波项，则回转误差中的一次谐振项也随之消去了，处理的结果仅含有回转误差中的2次及2次以上谐波成分，完全没有回转误差中的一次谐振项。

(3)转换坐标系后的一次谐波分离方法，通过坐标转换后，分离出了工作台面与轴线垂直度误差引起的正交一次谐波与轴系的一次谐振误差，完全保留回转误差的一次谐振、2次及2次以上谐波，使轴系倾角回转误差的数据处理方法更加合理和精确，是一种较理想的数据处理方法，当然处理出的回转误差也最大。

(4)通过实测8组数据的处理结果的对比，显示了分离出的轴系一次谐振运动的一致性，回转误差及其一次谐波的系数也基本相同，从而验证了转换坐标系后的一次谐波分离方法的正确性。

[参考文献]

[1] 陈剑雄,林述温,韩国强.基于球杆仪的旋转轴几何误差测量和辨识[J].计量学报,2014,35(3):198-203.

[2] 郭天太,王晓晓,洪博，等. 二维精密工作台离散点测量结果误差分离的新方法研究[J].计量学报,2014,35(2):113-119.

[3] Zhu J B,Zhang J H,Guo J K.Research of the influence of geometrical factors on rotary accuracy of high-precision spindle[C]//IEEE International Symposium on Assembly and Manufacturing,Xi’an, China,2013:264-269.

[4] 王欣,赵宏.轴类偏心零件偏心量测量方法及探测头误差分析研究[J]. 计量学报, 2015,36 (4): 360-364.

[5] Cappa S， Reynaerts D， Al-Bender F. A sub-nanometre spindle error motion separation technique[J].PrecisionEngineering,2014,38(3):458-471.

[6] 夏瑞雪,陈晓怀,卢荣胜，等.新型纳米三坐标测量误差检定方法的研究[J].电子测量与仪器学报,2010,24(3):250-256.

[7] 于博,于正林,顾莉栋，等.切线法数控成形非球面机床的定位误差补偿研究[J].计量学报, 2014,35 (6): 555-558.

[8] 孙艳玲，常素萍. 接触式表面轮廓测量的非线性误差分析与补偿[J]. 计量学报, 2016,37(6): 563-568.

[9] Jin L, Yan Z Y, Xie L M,etal. An experimental investigation of spindle rotary error on high-speed machining center[J].InternationalJournalofAdvancedManufacturingTechnology,2014, 70(4):327-334.

[10] Ma P, Zhao C M, Lu X H,etal. Rotation error measurement technology and experimentation research of high-precision hydrostatic spindle[J].InternationalJournalofAdvancedManufacturingTeconology，2014,73(9-12):1313-1320.

[11] 张景和,冯晓国,刘伟.用反向法测轴系回转误差[J].光学精密工程,2001,9(2):155-158.

[12] 雷贤卿,高作斌,马文锁,等.基于几何搜索逼近的球度误差最小区域评定[J].计量学报, 2016, 37 (2): 123-127.

[13] Chen D J, Fan J W, Zhang F H. An identification method for spindle rotation error of a diamond turning machine based on the wavelet transform[J].InternationalJournalofAdvancedManufacturingTechnology,2012,63:457-464.

[14] 任顺清,王俊柱.用水平仪测试倾角回转误差的数据处理[J].哈尔滨工业大学学报, 2006,38(6):837-839.

[15] 任顺清,房振勇,吴广玉,等.竖直轴系倾角回转误差的两种测试方法的比较[J]. 中国惯性技术学报,2000,8(3):74-78.

[16] 孙方金,陈世杰.精密轴系回转精度测试[M].黑龙江:哈尔滨工业大学出版社, 1997:32-34.

[17] GJB1801-1993 惯性技术测试设备主要性能测试方法[S]. 1993.