基于混沌分组教与学优化算法 锅炉NOx模型优化研究

马云鹏， 牛培峰， 陈 科， 闫姗姗， 李国强

(1. 燕山大学 电气工程学院， 河北 秦皇岛 066004； 2. 河北省桃林口水库管理局 水电厂， 河北 秦皇岛 066004)

1 引 言

近年来，学者们提出了多种改进的教与学优化算法，像A_TLBO，I_TLBO，MTLBO等[1～4]。为了平衡教与学优化算法的全局搜索能力和局部搜索能力，本文提出一种混沌分组教与学优化算法(chaos group teaching learning based optimization, CG-TLBO)，该算法采用3种调整机制：应用混沌方法对班级中的个体赋初值，增加了种群多样性，有益于算法跳出局部最小值，避免早熟收敛，益于提高全局搜索能力；在教阶段，引入自适应惯性权值，增强了算法的稳定性，有助于提高解的质量；在学阶段，采用随机蛙跳算法思想，将班级中的学生分组，类似现实中班级小组学习方式，有助于学生之间的信息交流，使得算法具有避免过早陷于局部极值的能力，从而增强了算法的局部搜索能力。为了验证改进算法的有效性，本文采用10个经典的测试集函数作为待优化函数，实验结果表明改进的教与学算法比人工蜂群算法、万有引力算法、原始的教与学优化算法收敛精度高，收敛速度快，具有良好的全局和局部搜索能力。

良好的数学模型才能反映锅炉真实的燃烧特性，为使循环流化床锅炉燃烧过程中排放的NOx达到国家规定的排放标准，建立较精确的NOx排放模型是前提。文献[4～7]分别采用自由搜索算法和万有引力算法优化基于支持向量机的NOx模型，较好地解决了NOx建模难的问题。本文采用改进的教与学优化算法优化基于极端学习机算法(extreme learning machine, ELM)[8]的NOx排放模型。其实质为：以影响NOx排放量的参数作为ELM的输入，NOx的排放浓度作为输出，应用改进的优化算法优化ELM的输入权值和隐层阈值，使ELM的输出逼近锅炉排放的NOx浓度，达到建模的目的。

2 混沌分组教与学优化算法

2.1 教与学优化算法

教与学优化算法是由Rao教授提出的一种新型群智能优化算法，它模拟了教师和学员之间的教学过程，目的是通过教师的“教”和学员之间的 “学”来提高学员的学习成绩[9]。在教阶段，班级中成绩最好的作为老师，通过老师的“教”，提高班里的平均成绩，同时使每个人都有提高;在学阶段，每个学员通过与其他学员比较，成绩差的向成绩好的学习，相互交流，共同进步。

2.2 混沌优化算法

混沌变量具有随机性、遍历性、规律性等特点，而且混沌优化算法具有全局渐进收敛和易跳出局部最优的优势[10]。因此，本文采用混沌序列初始化教与学优化算法的种群个体，增加种群的多样性，达到有效地进行全局搜索的目的。本文应用立方映射产生混沌序列，表达式为

X(t+1)=4X(t)3-3X(t)

(1)

式中：X(t)为第t个个体对应的混沌序列，X(t)∈[-1,1]；t=1,2,…,D，D是种群个数。

然后，对产生的混沌序列进行解空间变换，变换规则用公式(2)表示为

Xi=L+(1+Xi)(U-L)/2

(2)

式中：Xi为第i个待优化个体的解；U和L分别为搜索空间的上限和下限。

2.3 教阶段

这一阶段，学生成绩的更新主要依靠两部分：上一时刻的成绩Xold,i和老师与均值之间的差异(Mnew-TfMi)。为了提高教阶段的解的质量和稳定性，引入自适应惯性权值

Xnew,i=ωiXold,i+(1-ωi)(Mnew-TfMi)

(3)

ωi=1/[1+exp(-f(i)/a)×Niter]

(4)

式中：Xold,i为第i个个体未更新的解；Xnew,i为第i个个体更新后的解；Mnew为最好的个体，记为“老师”；Mi为班级平均成绩；Tf为教学系数；ωi为惯性权值，与当前的迭代次数Niter和第i个学生的适应度值f(i)有关，控制着前一时刻解的影响；a为第一次迭代中最大的适应度值。

2.4 学阶段

在学阶段，按照随机蛙跳算法的思想将学生分组，为提高学生们的学习积极性和学习成绩,分组是班级中常用的一种教学模式。组成员间互相交流信息，学习好的同学帮助学习差的，以达到共同进步的目的。类比于算法中，即为种群中的最优解调整最差解。将分组思想引入教与学优化算法，使该算法避免过早陷于局部极值，从而指引算法搜索过程向着全局最优方向进行。

Xw(j+1)=Xw(j)+rand(Xb(j)-Xw(j))

(5)

式中：Xb为组中最好的解；Xw为最差的解；rand为[0,1]之间的随机数。

3 性能测试

为了测试混沌分组教与学算法的性能，本文采用10个经典的测试集函数作为待优化函数，见表1。表1中,f1～f6为单峰高维的基准函数，f7～f10为多峰高维的基准函数，同时给出函数的理论最优值和自变量的取值范围。

表1 经典测试函数集

将改进算法与人工蜂群算法(ABC)、万有引力搜索算法(GSA)、原始教与学算法(TLBO)进行比较，各算法的参数设置见表2。表2中，Limit为ABC算法的预设参数，表示经过Limit次循环后，若解没有改进，则该个体被抛弃；G0和α为GSA算法中万有引力常量公式中的系数。所有测试及实验的运行环境为Microsoft Windows XP，AMD Athlon(tm) 64×2 Dual Core Processor 5000+、主频2.61 GHz、内存1.00 GHz的计算机上完成，仿真软件为MATLAB2009，每个仿真运行30次。测试结果见表3。表中，Mean表示30次运行结果的平均值，用来测试优化算法的收敛精度；S.D.为标准差的简写，表示30次结果的标准差，用来测试优化算法的稳定性。

表2 算法参数设置

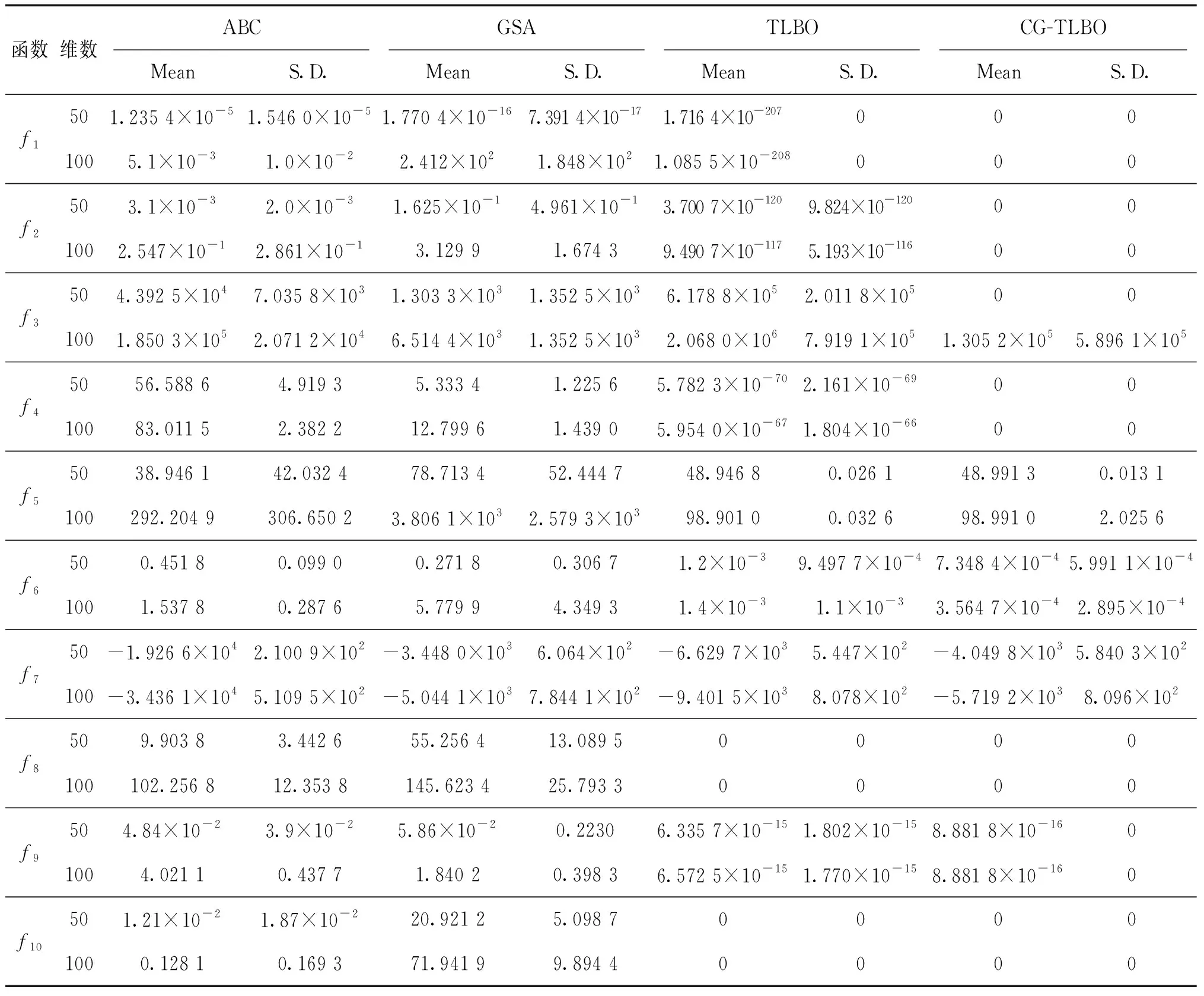
表3 测试结果

续表

表3给出了10个测试函数在50和100维下的测试结果。从测试结果来看，混沌分组教与学优化算法能够找到各函数在不同维度下的最优值或理论最优值，说明改进算法具有良好的收敛精度和鲁棒性。

图1和图2分别为f9取10维和f10取50维的仿真图，可以直观地显示出CG-TLBO收敛速度快，收敛精度高，具有良好的稳定性。

图1 函数f9为10维的性能对比图

图2 函数f10为50维的性能对比图

4 氮氧化合物建模

本文的研究对象为某电厂300 MW循环流化床锅炉，采集了给煤量、风量、床温、烟气含氧量等20个对氮氧化合物排放有影响的参量，共取数据288组。建模前，需对测试数据进行分配，231组作为训练样本，57组作为预测样本。采用改进的教与学优化算法(CG-TLBO)优化基于极端学习机(ELM)的NOx排放浓度模型，建模方法记为CG-TLBO-ELM。该方法的思想为：将20个对NOx排放有影响的参量作为ELM的输入，NOx的排放浓度作为ELM的输出;然后，采用CG-TLBO优化ELM的输入权值和隐层阈值，使ELM的输出值逼近NOx排放浓度的目标值。

假设极端学习机有n个输入神经元，有m个隐层神经元，则有(n+1)×m个参数需要优化，这些参数就是极端学习机的输入权值和隐层阈值。与此同时，需要设置优化问题的目标函数，一般采用训练样本的均方根误差作为优化问题的目标函数

(6)

式中：θ=(ω11,…,ω1,n,…,ωmn,b1,…,bm)为待优化参数；ωi=(ωi1,…,ωin)为第i个隐层节点对应的输入权值向量；m为隐层节点个数；n为输入层节点个数；Ntrain为训练样本个数；β为输出权值；g(x)为隐层激励函数；xj为第j个样本数据；tj为第j个样本对应的目标输出值。

为了验证优化后的极端学习机是否提高了模型精度，本文将原始的极端学习机(ELM)作为对比算法。设置极端学习机的隐层节点个数为20个，隐层激励函数为sigmoid函数。两种算法的测试对比图见图3和图4。

图3 NOx排放浓度训练模型对比

图4 NOx排放浓度预测模型对比

由图3可以看出，采用优化后的极端学习机算法建立的模型，训练精度比较好，说明较原始算法有良好的辨识能力；图4中，虽然个别点预测精度较差，但是总体效果是跟随的，且优于原始极端学习机算法，说明优化后的极端学习机具有良好的泛化能力。混沌分组教学优化算法达到了优化锅炉NOx排放浓度模型的目的，并且取得良好的效果。

5 结 论

为了提高原始教与学算法的全局和局部搜索能力，提出混沌分组教与学算法。采用混沌序列设置种群初始值，增加了种群多样性；引入自适应惯性权值，提高了解的质量；借鉴随机蛙跳算法思想，对班级分组，更新种群中的最差解，平衡了全局搜索与局部搜索的能力。改进算法用于优化循环流化床锅炉的氮氧化合物排放模型，即优化极端学习机的输入权值和阈值，提高了极端学习机的模型辨识能力和泛化能力。混沌分组教学优化算法具有收敛精度高，收敛速度快，全局和局部搜索能力强的特点。

[参考文献]

[1] Li G Q, Niu P F, Zhang W P,etal. Model NOxemissions by least squares support vector machine with tuning based on ameliorated teaching-learning-based optimization [J].ChemometricsandIntelligentLaboratorySystems, 2013, 126(8): 11-20.

[2] Rao R V, Patel V. An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems[J].ScientiaIranica, 2013, 20(3): 710-720.

[3] García J A M, Mena A J G. Optimal distributed generation location and size using a modified teaching-learning based optimization algorithm[J].Internationaljournalofelectricalpower&energysystems,2013, 50(1): 65-75.

[4] 牛培峰,王培坤,李国强,等.基于自由搜索算法和支持向量机的燃煤锅炉NOx建模与优化[J]. 计量学报,2014,35(6):626-630.

[5] 牛培峰,麻红波,李国强,等.基于GSA-SVM的循环流化床锅炉NOx排放特性模型[J].计量学报,2013,34(6):602-606.

[6] 牛培峰，王丘亚，马云鹏，等.基于量子自适应鸟群算法的锅炉NOx排放特性研究[J]. 计量学报, 2017,38(6):770-775.

[7] 牛培峰，马云鹏，张京，等.基于相关向量机的电站锅炉NOx燃烧优化[J]. 计量学报, 2016,37(2):626-630.

[8] Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: a new learning scheme of feedforward neural networks[C]//IEEE International Joint Conference on Neural Networks. Budapest,Hungary,2004:985-990.

[9] 拓守恒, 雍龙泉, 邓方安. “教与学” 优化算法研究综述[J]. 计算机应用研究, 2013, 30(7): 1933-1938.

[10] 冯艳红, 刘建芹, 贺毅朝. 基于混沌理论的动态种群萤火虫算法[J]. 计算机应用, 2013, 33(3): 191-196.