GUM法和MCM法评定测量不确定度对比分析

刘园园， 杨 健， 赵希勇， 赵士伟

(中国白城兵器试验中心， 吉林 白城 137001)

1 引 言

不确定度是一个合理表征测量结果的分散性参数，测量结果的可用性在很大程度上取决于其不确定度的大小。因此，在给出测量结果时，只有附加不确定度的说明才是完整和有意义的。同时，测量不确定度评定和表示方法的一致，是科技交流和国际贸易进一步发展的要求，使得不同国家所得到的测量结果可以方便地进行相互比较、相互承认并达到共识。各国际组织和各国的计量部门均十分重视不确定度评定方法和表示方法。1993年，7个国际组织联合发布《测量不确定度表示指南》(Guide to the expression of uncertainty in measurement)简称GUM；1995年，对GUM进行了修订；2008年计量学指南联合委员会(JCGM)对GUM(95)做了修改，并发布了GUM的附件1《用蒙特卡洛法传播概率分布》(Supplement 1: Propagation of distributions using a Monte Carlo method)；2009年发布ISO/IEC Guide 98-1:2009 对测量不确定度表示指南的介绍；2011年JCGM发布了GUM的补充条款2；2012年发布ISO/IEC Guide 98-4:2012 测量不确定度在合格评定中的作用。为取得国际市场中的平等地位和经济活动中的竞争优势，就必须走国际化、与世界接轨的道路，这就要求我国出具的各类测试报告、检定证书、校准证书、技术规范、产品标准乃至合同或协议等文件中，都应当采用国际公认的有关测量结果和测量不确定度的表述方法。为此，我国于1991年制定了JJG 1027—1991《测量误差及数据处理》，1999年发布JJF 1059—1999《测量不确定度评定与表示》，代替了JJG 1027—1991中数据处理部分。2012年底发布了JJF 1059.1—2012《测量不确定度评定与表示》代替了JJF 1059—1999，发布了JJF 1059.2—2012《用蒙特卡洛法评定测量不确定度》，作为JJF 1059.1-2012的补充件[1～5]。在气象计量检定领域，主流的评定测量不确定度方法为GUM法和MCM法，本文先对GUM法和MCM法进行了简要介绍，然后以气象检定领域中的风速不确定度评定为例，分别在输入量正态分布以及其他分布两种假设情况下，对比分析了GUM法与MCM法评定风速简化模型测量不确定度结果，并对简化模型所忽略的水汽修正项带来的测量不确定度进行了量化，通过实例对比分析，综合评定两种方法在适用范围、可操作性以及结果可信度等方面的表现。

2 GUM法

通过不确定度传播率计算合成标准不确定度，从而得到被测量估计值的测量不确定度的方法称为不确定度指南的方法，简称GUM法。GUM法评定测量不确定度的步骤：

(1)分析不确定度来源和建立测量模型Y=f(X1,X2,…,XN)；

(2)评定标准不确定度：计算灵敏系数ci，评定测量模型中的各输入量的标准不确定度u(xi)，给出与各输入量相对应的输出量y的不确定度分量ui；

(3)计算合成标准不确定度uc；

(4)确定k或者kP， 计算扩展不确定度U或UP。

GUM法主要适用条件为：(1)可以假设输入量的概率分布呈对称分布；(2)可以假设输出量的概率分布近似为正态分布或t分布；(3)测量模型为线性模型、可以转化为线性的模型或可用线性模型近似的模型。有关GUM法的详细说明见2013-06-03起开始实施的JJF 1059.1—2012《测量不确定度评定与表示》。

3 MCM法

蒙特卡洛法(Monte Carlo method，简称MCM)，是采用概率分布传播的方法，通过对输入量Xi的概率密度函数PDF离散抽样，由测量模型传播输入量的分布，计算获得输出量Y的PDF离散抽样值，进而由输出量的离散分布数值直接获取输出量的最佳估计值、标准不确定度和包含区间。该输出量的最佳估计值、标准不确定度和包含区间等特性的可信程度随PDF抽样数的增加可得到改善。MCM是通过如下步骤实现概率分布的传播和不确定度的评定：

(1)建立Y和X1,X2,…,XN之间的测量模型Y=f(X1,X2,…,XN)；

(2)利用可获得的信息，为Xi设定PDF，如正态分布、均匀分布、t分布、反正弦分布、三角分布、梯形分布等；

(3)选择蒙特卡洛试验样本量的大小M，从输入量Xi的概率密度函数gXi(ξi)中抽取个M样本值xir,i=1,2,…,N,r=1,2,…,M值。对每一个样本值(x1r,x2r,…,xNr)，计算相应输出量Y的模型值yr=f(x1r,x2r,…,xNr),r=1,2,…,M；

(4)将这些M个模型值按严格递增次序排序，由这些排序的模型值得到输出量Y的分布函数的离散表示G。由G计算输出量Y的估计值y、标准不确定度u(y)以及在约定包含概率P时Y的包含区间[ylow,yhigh]。

用蒙特卡洛法评定测量不确定度时必须由相应的计算软件进行计算，测量结果不用合成标准不确定度和扩展不确定度表示，而是用被测量的估计值y、标准不确定度u(y)以及包含区间[ylow,yhigh]表示，由于样本是随机抽取的，计算得到的包含区间不一定是完全对称的。

有关MCM法的详细说明见2013-06-21起开始实施的JJF 1059.2—2012《用蒙特卡洛法评定测量不确定度》。

4 GUM法与MCM法实例对比分析

为了分析比较GUM法与MCM法评定不确定度的优劣，以气象计量检定领域中标准皮托管测量风速的不确定度评定为例，分别用以上两种方法进行评定。风速V/m·s-1的计算模型如下：

(1)

本文只研究在动压值为227.1 Pa、皮托管系数为1.001、温度为24.2℃、气压为973.2 hPa和相对湿度φ为46.3%的情况下，对风速计算结果进行不确定度评定，不涉及重复性和风洞均匀性等带来的不确定度。由技术资料可知，该微差压计为0.01级标准，皮托管系数的测量误差为±0.1%，气压、温度、湿度测量仪器的最大允许误差分别是±0.4 hPa、±0.3℃和±3%RH。

4.1 输入量正态分布时GUM法与MCM法的比较

4.1.1 GUM法评定风速简化模型的测量不确定度

(1)因为在用GUM法评定不确定度的过程中，涉及求取灵敏系数的偏导运算，较之水汽修正项0.378e较小，在实际的评定过程中常简化测量模型为:

(2)

(2)各个输入量的灵敏系数分别为：

假设全部输入量都服从正态分布，k=2，可得：

u(pd)=0.005%×pd=0.005%×227.1 Pa

=0.011 355 Pa;

u(J)=0.05%×J

=0.05%×1.001=0.000 500 5;

其中,T=273.15+t, K。

(3)风速V的估计值v的合成标准不确定度为:

也可计算相对合成标准不确定度为：

=0.037%

(4)为了和MCM法相比较，计算对应95%概率包含区间，此时k=1.96，区间为[19.954 6，19.983 6]。

4.1.2 MCM法评定风速简化模型的测量不确定度

(1)建立模型见式(2)。

(2)确定各输入量密度分布函数分别为：pd～N(227.1, 227.1×0.005%)；J～N(1.001, 1.001×0.05%)；t～N(24.2, 0.15)；p～N(973.2, 0.2)。

(3)确定抽样样本M=106，编程随机抽取M个pdr、Jr、tr、pr，并计算相应风速的值Vr，r=1,2,…,M。

(4)编程计算风速V的估计值v、标准不确定度u(v)以及在约定包含概率为95%时V的包含区间[vlow,vhigh]，结果见表1。

表1 GUM法与MCM法结果对比 m·s-1

(5)图1给出了用GUM法获得的风速正态概率密度函数(弧线区域)，以及由MCM法提供的用M=106个模型值组成的离散概率分布(阶梯线区域)，由图可见，两种方法得到的概率密度直观上难以区分，验证了简化模型时，两种方法是一致的。此时，认为GUM法是通过MCM法验证的。

图1 简化模型时GUM法正态概率分布图 和MCM法离散概率分布图

4.2 改变输入量分布时GUM法和MCM法比较

简化模型时，GUM法和MCM法结果基本吻合，但是并不能由此就得到两种方法等同的结论，因为简化模型可以转化为线性模型，并且所有输入量分布都假设为正态分布，这正是GUM方法适用的场合。针对这种情况，改变输入量分布，查看不满足GUM方法适用条件时两种方法的结果对比。

选择如下3种方案，不具有实际意义，分别用两种方法评定风速不确定度，结果见表2和图2～图4。

方案1:改变皮托管系数分布为反正弦分布，其他不变。

方案2:改变皮托管系数分布为反正弦分布，温度分布为反正弦分布，其他不变。

方案3:改变皮托管系数分布为反正弦分布，温度分布为均匀分布，其他不变。

表2 不同方案GUM法与MCM法结果对比 m·s-1

图2 方案1时GUM法正态概率分布图 和MCM法离散概率分布图

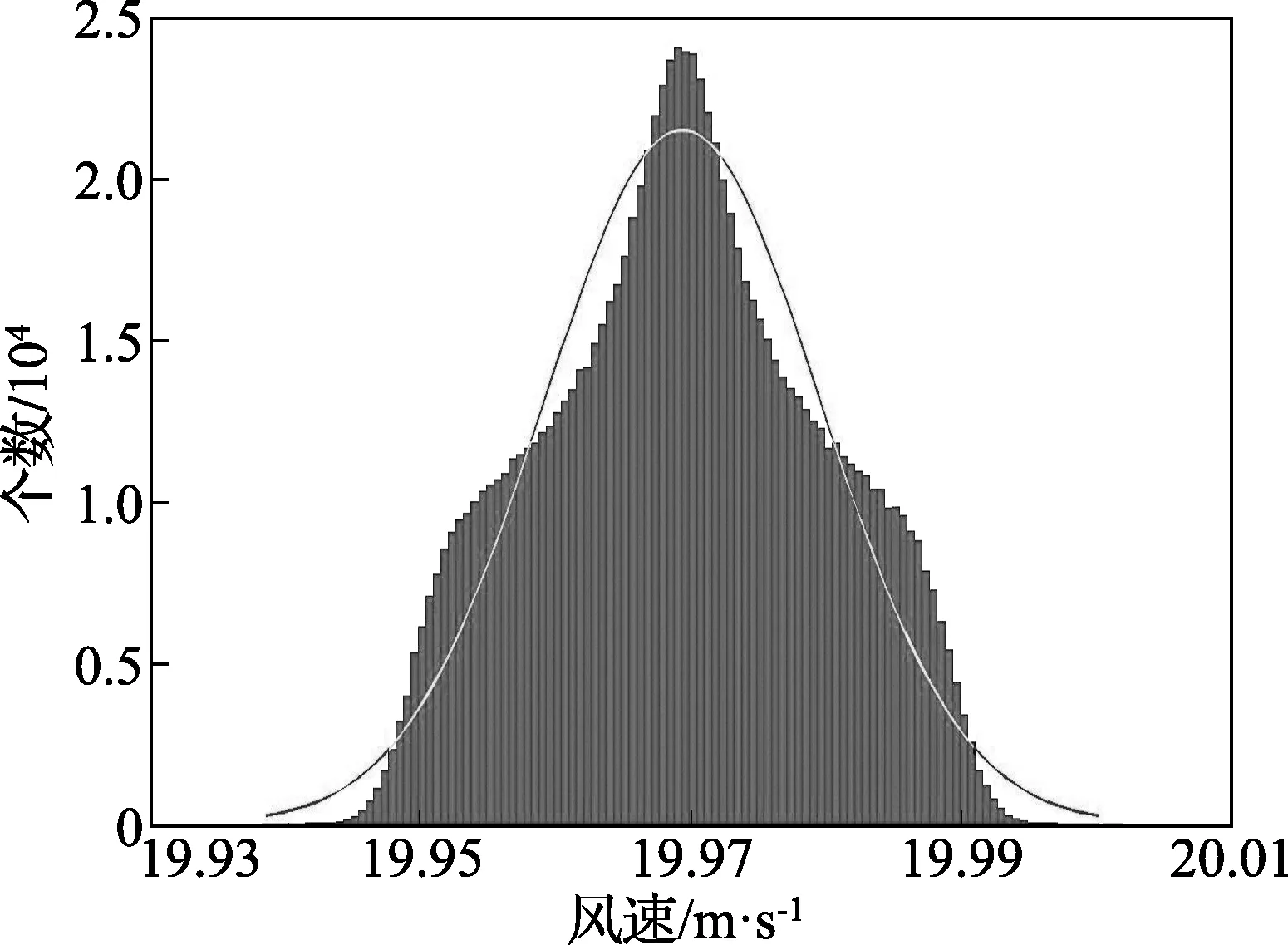
图3 方案2时GUM法正态概率分布图 和MCM法离散概率分布图

图4 方案3时GUM法正态概率分布图 和MCM法离散概率分布图

由图表可知，3种方案中，GUM法和MCM法结果差异比较大。MCM法得到的离散概率分布明显不是正态分布，与GUM法的正态概率分布有很大差异，同时MCM法得到95%概率对称包含区间也较GUM法的要短一些。由GUM法的评定步骤可知，只有输入量分布的标准差参与了计算，分布的其他各种信息都被忽视了，所以GUM得到的概率分布总是近似为正态分布或t分布。而MCM法是随机抽取足够多的输入量分布的样本，然后再计算出的输出量分布，其中所抽取的输入量样本基本能代表输入量分布的全部信息，所以这样得到的输出量的评定结果更为真实可信，这也体现了GUM法的局限性和MCM法的灵活性。但两种方法得到的风速标准不确定度几乎一样，主要是由于使用GUM法时不存在采用泰勒级数展开，并舍去高次项才得到近似线性模型这个步骤，所以在不确定度传播中，没有舍弃误差。

4.3 MCM法评定考虑水汽修正项模型的风速不确定度

以上都是对简化模型来讨论的，那么简化模型舍弃的水汽修正项对测量结果有多大的影响，简化是否合理呢？下面将评定考虑水汽修正项的风速不确定度。由于水汽修正项形式复杂，导致温度和湿度参数的灵敏系数不可操作，也就无法用GUM法进行不确定度的评定，只能用MCM法。此时，仍假设全部输入量都服从正态分布，增加湿度输入量分布φ～N(46.3, 1.5)，其他基本同4.1.2节，评定结果见表1和图5。

图5 式(1)模型时MCM法离散概率分布直方图

由图5可以看出，即使式(1)模型不是线性模型，但在输入量都是正态分布的假设下，MCM法得到的风速离散概率分布和正态概率分布基本吻合。由表1可以看出，两模型的风速估计值相差为(20.023 5-19.969 1) m·s-1=0.054 4 m·s-1,考虑水汽修正项带来的标准不确定度为(0.008 0-0.007 4) m·s-1=0.000 6 m·s-1，这样就将水汽修正项对测量结果的影响进行了量化，可以根据实际需求来决定是否需要考虑水汽修正项。MCM法不需要繁琐的求导过程，也就不需要为了简化求导而舍弃一些小影响量的不确定度计算，可以将所有影响因素都考虑进来，使不确定度评定结果更完整合理。这也体现了MCM法较GUM法更具有可操作性。

5 结 论

在气象计量检定领域，不确定度的评定是必不可少的，目前用来评定不确定度的方法主要有GUM法和MCM法，在实际工作中，需要根据不同条件选择相应的评定方法。从上面例子可以得出，在输入量的概率分布为对称分布、输出量的概率分布近似为正态分布或t分布和测量模型为线性模型或可用线性模型近似表示的情况下，GUM法和MCM法均适合用来评定其测量不确定度，并且结果基本吻合；在其他情况下，例如模型非线性或者输入量为均匀分布、反正弦分布等，应当慎重选择评定方法，通常利用MCM法对GUM法评定结果进行验证，当验证结果一致时，可以采用GUM法进行不确定度评定，否则应当采用MCM法。综合来看，MCM法较GUM法适用范围广，可操作性强，结果可信度高，特别是针对一些复杂模型MCM法不需要繁琐的求导过程，也就不需要为了简化求导而舍弃一些小影响量的不确定度计算，可以将所有影响因素都考虑进来，使不确定度评定结果更完整合理。

[参考文献]

[1] 国家质量监督检验检疫总局.JJF 1059.1—2012 测量不确定度评定与表示[S].

[2] 国家质量监督检验检疫总局.JJF 1059.2—2012 用蒙特卡洛法评定测量不确定度[S].

[3] 方兴华，宋明顺，顾龙芳,等.基于自适应蒙特卡罗方法的测量不确定度评定[J].计量学报,2016,37(4):452-456.

[4] 倪育才.实用测量不确定度评定[M].北京:中国计量出版社,2009:5-9.

[5] 沙定国.误差理论与测量不确定度评定[M].北京:中国计量出版社,2003:12-17.