基于分形维数和GA-SVM的风电机组 齿轮箱轴承故障诊断
2018-06-22时培明安淑君
时培明, 梁 凯, 赵 娜, 安淑君
(燕山大学 电气工程学院, 河北 秦皇岛 066004)
1 引 言
由于风机受无规律的变向、变速和变载荷的风力作用以及强阵风的冲击,工况极不稳定。复杂工况下的风机齿轮箱轴承故障诊断难度很大,误诊率很高。近年来,很多学者应用支持向量机对机械故障进行诊断取得了很好的效果[1~7]。
本文提出一种基于遗传算法自动求解支持向量机的最佳参数的支持向量机模型(genetic algorithm support vector machine,GA-SVM)。根据分形维数理论、盒维数的计算和常用的时域特征参数的计算,采用河北省张家口某风场的风电机组齿轮箱轴承数据进行故障诊断,通过实验对比论证:盒维数能够提高支持向量机故障诊断的准确率;基于GA-SVM的模型能有效提升分类的准确率。
2 GA-SVM模型理论概述
2.1 支持向量机
基于Vapnik等人提出的统计学习理论的支持向量机(support vector machine,SVM)方法是一种比较好地实现了结构风险最小化思想的方法,为解决小样本分类、非线性问题提供了思路。
假设给定的m个样本训练集为:
T={(xi,yi)|i=1,2,…,m}
式中:xi∈RN为N维样本坐标向量;yi∈{-1,1}。
假设样本训练集能被某个超平面H:w·x+b=0(w为权重系数向量;x为样本坐标向量;b为偏置项)没有错误地分开,并且离超平面最近的向量与超平面之间的距离是最大的,该超平面就称为最优超平面。
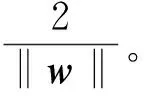
yi[(w·xi)+b]≥1
(1)
因此,支持向量机的目的是采用式(2)构建能对所有样本正确分类的分类超平面:
(2)
由于目标函数和约束条件都是凸的,根据最优化理论,这一问题存在唯一的全局最小解。应用Lagrange乘子并考虑满足KKT条件:
αi·{yi[(x·xi)+b]-1}=0
(3)
式中:αi为拉格朗日乘子。
可求得最优超平面决策函数为:
M(x)=sgn[(w*·x)+b*]
(4)
式中:w*为权重系数向量;b*为偏置项;αi*为拉格朗日乘子。
对于线性不可分情况,通过引入松弛变量ξi≥0,修改目标函数和约束条件,应用完全类似的方法求解。
(5)
式中:C为惩罚系数。
在训练数据不可分的情况下,由于允许错分,因此相当于在刨除那些错分样本的情况下,最大化分类间隔超平面。
对非线性情况,支持向量机利用了特征空间中的非线性映射算法,即通过事先选择的某种非线性映射将输入的向量x映射到一个高维特征空间Z,即φ:RN→Z,x→φ(x)。而后在此高维空间中使用线性支持向量机进行分类。
2.2 GA-SVM模型
GA-SVM模型见图1。

图1 GA-SVM模型
SVM能否出色完成训练测试任务,构造SVM的核函数参数g、惩罚因子c有重要影响。因为很难预先确定合适的参数c、g,所以本文中采用GA算法对SVM中的参数进行优化,其具体步骤如图1所示。这样可以有效弥补在构造核函数参数及惩罚因子时因经验不足而导致分类准确率偏低。GA的基本思路是从一个群体出发,然后通过自然选择、交叉和变异等遗传操作产生新一代群体。群体中包含多个个体,每个个体代表优化问题的一个解,即遗传学中的染色体。在进行选择操作时,采用适应度函数方式对每个个体代表优化问题的一个解,即遗传学中的染色体。在进行选择操作时,采用适应度函数方式对每个个体进行适应度评价,通过适应度函数值来决定适用于产生下一代的父代个体,适应度函数值较小的则被淘汰。然后将选择出的个体经过交叉和变异等操作产生新的一代。新一代群体继承了上一代中优良特性,这样遗传操作使优化朝着更优解方向进化[8~11]。
3 基于分形维数与GA-SVM的风电机组齿轮箱轴承故障诊断算法
3.1 提取特征参量
3.1.1 时域特征参数提取
要实现故障智能诊断首先需要故障特征提取。以下是常用的时域特征参数及计算方法。
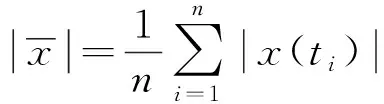
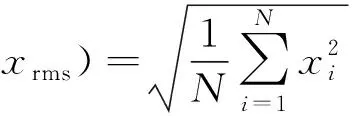
峰值:xF=|xmax|
峰峰值:xF-F=|xmax-xmin|
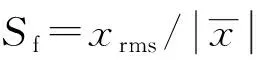
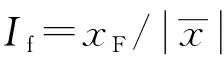
裕度指标:CLf=xF/xr
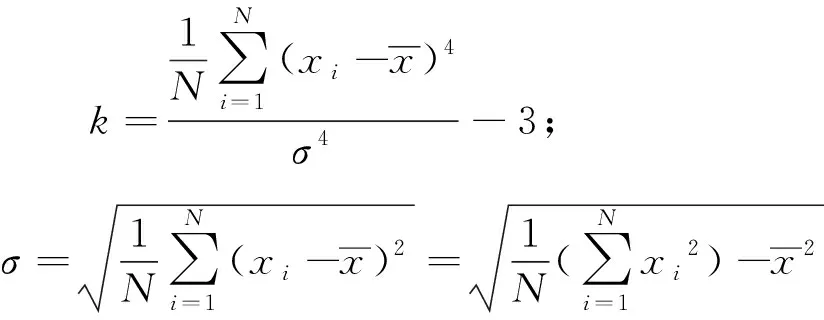
3.1.2 盒维数提取
将分形维数作为反映系统故障的特征量,通过系统分形维数的变化来判断系统是否偏离了正常状态,即是否出现了故障。盒维数在众多分形维数中是最简单且应用最广的一种[12],因此本文采用盒维数作为故障的特征参量。
设X是n维欧式空间Rn上的闭集,将Rn划分成尽可能细的δ网格,若N(δ)是网格宽度为δ的集合X的网格计数,盒维数定义为:
(6)
3.2 诊断算法流程图
本文利用GA-SVM模型对风电机组齿轮箱轴承的故障进行模式识别分类,风电机组齿轮箱轴承的振动数据作为该诊断模型的输入变量,输出为风电机组齿轮箱轴承的故障状态,建立诊断模型。基于GA-SVM的风电机组齿轮箱轴承故障诊断流程图如图2所示。
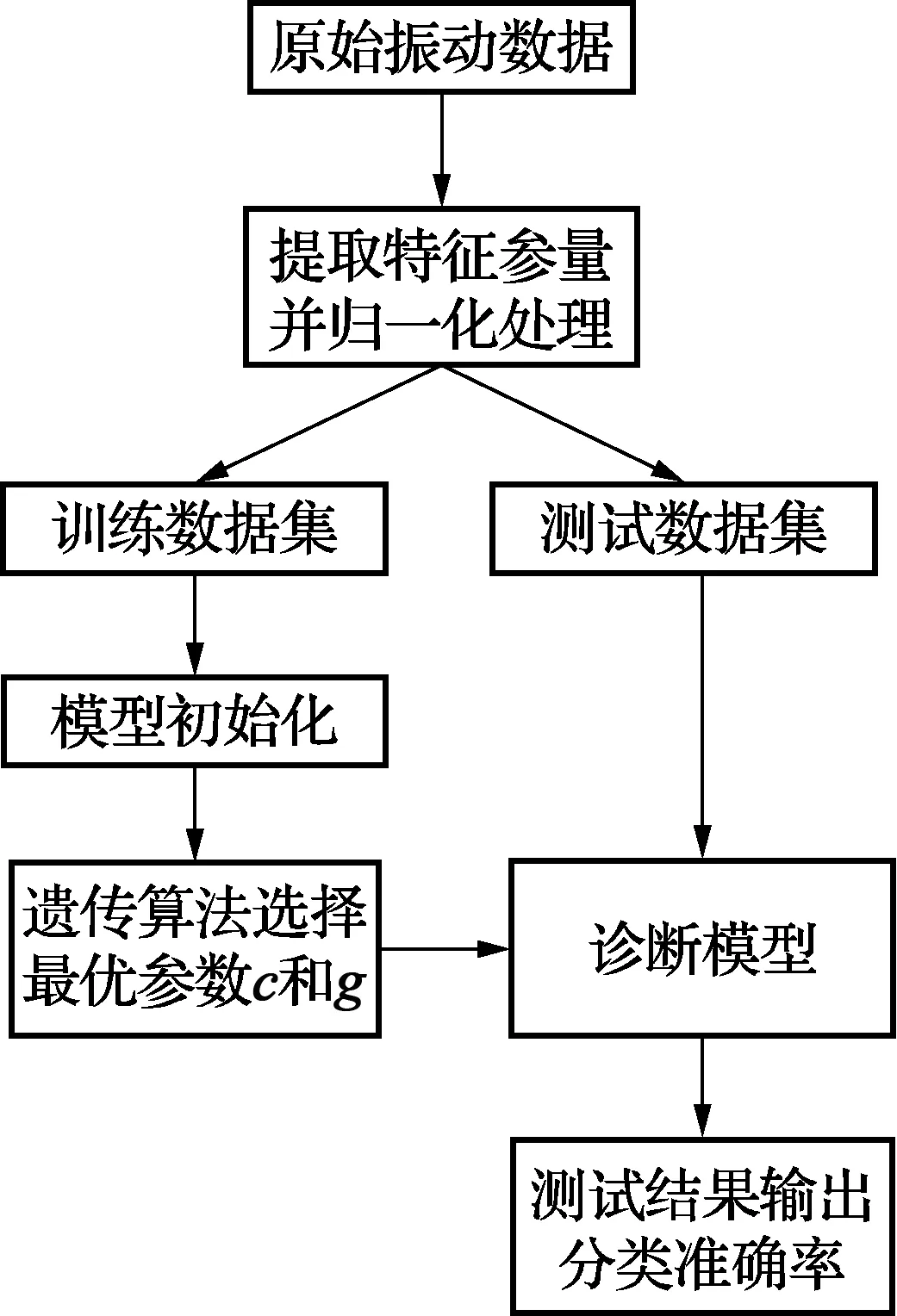
图2 基于GA-SVM的风电机组齿轮箱 轴承故障诊断流程
(1)分别采集齿轮箱轴承在正常以及故障状态下的原始振动数据为样本。
(2)求解原始振动数据的时域特征参数及盒维数。利用式(7)对提取的特征参量行归一化:
(7)
式中,xig表示归一化的特征参量;xi表示各特征参量的能量值;xmax,xmin表示xi中的最大最小值。
(3)将提取的特征参量数据集进行划分,分别为用于训练的数据集和用于测试的数据集。
(4)对GA的参数选项进行初始化设置:遗传算法参数设置为进化代数为200,种群数为20,交叉概率为0.9,变异概率为0.01,惩罚因子c的取值范围为(0,100],径向基参数g的取值范围为[0,1 000], 以支持向量机的平均相对误差作为适应度函数。
(5)利用遗传算法选择出最佳参数c和g。
(6)利用训练数据通过上述步骤生成风电机组齿箱轴承故障诊断模型。
(7)将测试数据集输入到训练好的风电机组齿轮箱轴承故障诊断模型中,进行故障诊断,输出测试结果。
4 风电机组齿轮箱轴承故障诊断实例
4.1 风电机组齿轮箱轴承故障诊断特征提取
选取河北省张家口某风电场的风力发电机组发电机前轴承垂直方向测点的振动数据,一共选取了63组数据:故障数据(1~23)和正常数据(24~63)。故障类型定为标签一,正常类型定为标签二。随机选取故障数据中的10组和正常数据中的20组为训练集;剩余的为测试集。对振动信号故障特征进行提取,限于篇幅,故障轴承与正常轴承各列举2组数据,见表1。
4.2 故障诊断对比试验
为了证明分形维数对于提升SVM性能的有效性,分两组实验进行对比论证:第一组,选取9项时域指标作为特征参数;第二组,选取9项时域指标外加盒维数作为特征参数。结果见图3和图4。
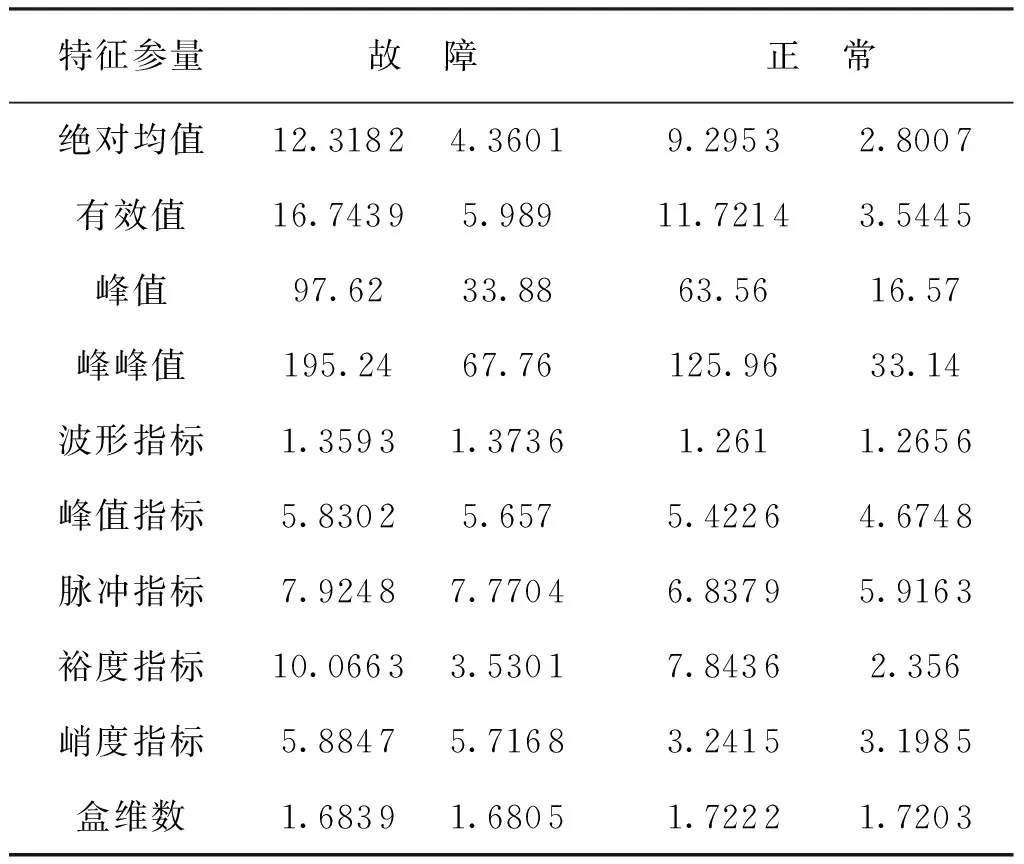
表1 两种类别的特征参量
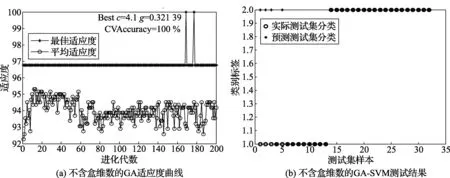
图3 不含盒维数的GA适应度曲线及不含盒维数的GA-SVM测试结果

图4 含盒维数的GA适应度曲线及含盒维数的GA-SVM测试结果
对比图3和图4可知含盒维数的GA适应度曲线明显好于不含盒维数的GA适应度曲线,并且含盒维数的GA-SVM测试结果93.75%(30/32)好于不含盒维数的GA-SVM测试结果87.5%(28/32)。易知,盒维数特征参数能提升支持向量机的性能,提高故障诊断准确率。
为了证明遗传算法能有效找到最优参数,提高SVM的分类准确率,分3组实验进行对比论证:第一组选取c=1,g=1;第二组选取c=2,g=2;第三组应用遗传算法求出最优参数。故障诊断结果见表2。
由表2可知,不同的径向基核参数和惩罚因子影响SVM的适应度曲线和分类准确率;GA-SVM模型能通过遗传算法找出最佳参数,从而提高故障分类的准确性。

表2 不同支持向量机故障诊断结果
5 结 论
(1)引入遗传算法对SVM核函数参数、惩罚因子进行优化,建立GA-SVM模型,能有效提升分类的准确率,能更好地识别故障。
(2)结果表明:通过对比实验可知添加盒维数特征参量能提升SVM的性能,提高支持向量机的故障诊断准确率。 这表明变工况条件下,盒维数能够表征齿轮箱轴承的特征,盒维数是有效的特征参数。
(3)提升故障诊断的准确率关键在两个方面:支持向量机的核函数参数、惩罚因子的选取和有效特征参数的选取。
[参考文献]
[1] Saravanan N. Gear Box Fault Diagnosis using Hilbert Transform and Study on Classification of Features by Support Vector Machine [J]. InternationalJournalofHybridInformationTechnology, 2014, 7 (4): 69-82.
[2] Zhang L B. Gear Fault Diagnosis Using Empirical Mode Decomposition, Genetic Algorithm and Support Vector Machine [J].JournalofVibrationMeasurement&Diagnosis, 2009, 29 (4): 445-448.
[3] Chen F, Tang B, Chen R. A novel fault diagnosis model for gearbox based on wavelet support vector machine with immune genetic algorithm [J].Measurement, 2013, 46 (1):220-232.
[4] 王凯, 张永祥, 李军. 遗传算法和支持向量机在机械故障诊断中的应用研究[J]. 机械强度, 2008, 30(3): 349-353.
[5] 陈果, 周伽. 小样本数据的支持向量机回归模型参数及预测区间研究[J]. 计量学报, 2008, 29(1): 92-96.
[6] 王凯, 张永祥, 李军. 基于支持向量机的齿轮故障诊断方法研究[J]. 振动与冲击, 2006, 25 (6): 97-99.
[7] 孟宗,季艳,谷伟明,等. 基于支持向量机和窗函数的DEMD端点效应抑制方法[J]. 计量学报, 2016, 37(2):180-184.
[8] 严刚峰, 黄显核, 谭航,等. 基于遗传算法的振荡器谐振回路的参数选择[J]. 计量学报, 2010, 31(2): 165-169.
[9] 南国芳, 王化祥, 王超. 基于BP神经网络和遗传算法的电阻抗图像重建算法[J]. 计量学报, 2003, 24(4): 337-340.
[10] 田社平, 韦红雨, 颜德田. 基于遗传算法的lp数据拟合及其应用[J]. 计量学报, 2005, 26(3): 284-288.
[11] 卢桂馥, 王勇, 窦易文. 基于遗传算法和最小二乘支持向量机的织物剪切性能预测[J]. 计量学报, 2009, 30(6) :543-546.
[12] 于德介, 程军圣, 杨宇. 机械故障诊断的Hilbert-Huang变换方法[M]. 北京:科学出版社, 2007: 137-138.
