基于参数Zc预测25Cr35Ni耐热钢的蠕变行为与持久寿命

，，，，，

(1.大连理工大学材料科学与工程学院，大连 116085；2.中国汽车技术研究中心，天津 300300)

0 引 言

高温材料在很多领域得到了应用，其发展受到了研究人员的广泛关注，其强度、使用寿命等性能的评估成为工程和学术研究领域关注的主要问题。

传统高温材料的使用寿命主要借助高温蠕变试验[1]来进行评估。常见的预测高温蠕变持久寿命的方法包括TTP参数法、θ法、Wilshire法等[2-5]，这些方法已成功应用在很多工程领域[6-7]。然而，这些预测方法大多使用蠕变断裂时的时间数据进行预测，耗时较长，且忽略了大量蠕变信息；虽然θ法结合了高温蠕变信息并在一些材料中得到了较好的应用，但在处理某些高温材料的蠕变曲线时，会出现预测精度不高的问题[5, 8]，且无法实现性能的可靠性评估。

为此，作者以25Cr35Ni耐热钢为研究对象，在不同温度和不同应力下进行了蠕变试验，在对不同蠕变应变下的温度和时间进行归一化处理的基础上，引入参数Zc分析了数据的分散程度并使用蠕变应变为5.0%下的试验数据对持久寿命进行了预测。

1 试样制备与试验方法

试验材料为离心铸造的25Cr35Ni耐热钢管，规格为φ68 mm×10 mm，长3 000 m，采用XRF-1800型荧光光谱仪测得其化学成分如表1所示。在试验钢管上取样，打磨抛光后，用质量分数为10%的草酸水溶液中进行电解腐蚀，电压为5 V，使用MEF-3型光学显微镜观察横截面的显微组织。由图1可见，25Cr35Ni耐热钢的显微组织由奥氏体基体和骨架状共晶碳化物组成。

按照GB/T 2039-1997，在25Cr35Ni耐热钢管上沿轴向加工出标准蠕变试样，标距为(25±0.2) mm，直径为(5±0.2) mm，在RSW-500型蠕变持久试验机上进行蠕变试验，试验温度为900～1 100 ℃，误差在±1 ℃，应力为25～80 MPa。

表1 25Cr35Ni耐热钢的化学成分(质量分数)Tab.1 Chemical composition of 25Cr35Ni heat-resistantsteel (mass) %

图1 25Cr35Ni耐热钢的显微组织Fig.1 Microstructure of 25Cr35Ni heat-resistant steel: (a) at low magnification and (b) at high magnification

2 试验结果与讨论

2.1 蠕变曲线

由图2可以看出，应力和温度越低，试样稳态蠕变阶段持续的时间越长，其持久断裂寿命也越长。

图2 在不同温度和不同应力下试样的蠕变曲线Fig.2 Creep curves of samples at different temperatures and different stresses

2.2 蠕变数据处理及数据分散性

采用Larson-Miller参数形式对各蠕变应变下的时间和温度进行归一化处理[2]，计算公式为

P=10-3×T×(lgts+C)

(1)

式中：P为归一化参数；T为试验温度，K；ts为蠕变时间，h；C为Larson-Miller常数，取20[6]。

由图2得到蠕变应变分别为0.1%，0.2%，0.5%，1.0%，2.0%，5.0%时对应的ts，以及试样断裂时对应的时间(持久寿命)，与T一起代入式(1)，计算得到对应的P。

图3 不同蠕变应变下试样的σ和P的关系Fig.3 Relationship between σ and P of samples at different creep strains

以应力σ为纵轴，P为横轴建立直角坐标系。由图3可知：随蠕变应变的增加，(P，σ)数据点逐渐靠近试样蠕变断裂时的数据点，当蠕变应变为5%时，(P，σ)数据与蠕变断裂时的数据十分接近。

根据文献[9]并综合考虑数据的相关性，建立数学模型对不同蠕变应变下的σ和P进行拟合，拟合公式为

lgσ=a+0.411 5P-0.009 48P2

(2)

式中：a为拟合常数。

拟合曲线绘于图3。由图3可见：各蠕变应变下的(P，σ)数据点分布于拟合曲线的两侧，且在较小蠕变应变下(P，σ)数据点的分散程度较大；在较高应力下，随蠕变应变的增加P增长得较快，在较低应力下则较慢。与高温高应力相比，高温低应力下试样达到同样的蠕变变形时所需的时间更长；长时间的服役会引起组织老化，导致试样抵抗变形的能力减弱，此时试样再达到相同应变时所需的时间缩短。因此，在低应力下P随蠕变应变的增加而缓慢增大。

引入参数Zc对高温蠕变变形进行预测。Zc的物理意义为σ-P曲线相对于蠕变应变为0.1%时的σ-P曲线的偏移量，其计算公式为

Zc=a-a0.1%

(3)

式中：a0.1%为蠕变应变为0.1%时σ-P曲线的拟合常数。

将不同蠕变应变下σ-P曲线的拟合常数代入式(3)，计算得到不同蠕变应变下的Zc。由图4可知，随蠕变应变的增加，Zc先迅速增大后趋于平缓。结合图3分析可知：Zc的大小可用于表征σ-P曲线与蠕变断裂时曲线的偏移程度，Zc越大，σ-P曲线越靠近蠕变断裂时的曲线；Zc的变化速率可用于表征σ-P曲线向蠕变断裂时曲线的偏移速度，当Zc变化趋于平缓时，σ-P曲线与蠕变断裂时的曲线十分接近。

图4 Zc随蠕变应变的变化曲线Fig.4 Curve of Zc vs creep strain

作者所在课题组在前期研究时发现，持久寿命数据在主曲线两端呈正态分布[9-10]。将相同P下的实际应力与拟合得到的应力之间的差值定义为σ，以蠕变应变为0.1%，1.0%，5.0%时σ的概率密度分布对(P，σ)数据点与其拟合曲线间的分散程度进行分析。由图5可知，随着蠕变应变的增加，σ的正态分布曲线变得尖锐，表明(P，σ)数据点的偏差程度减小，数据的分散程度减小。

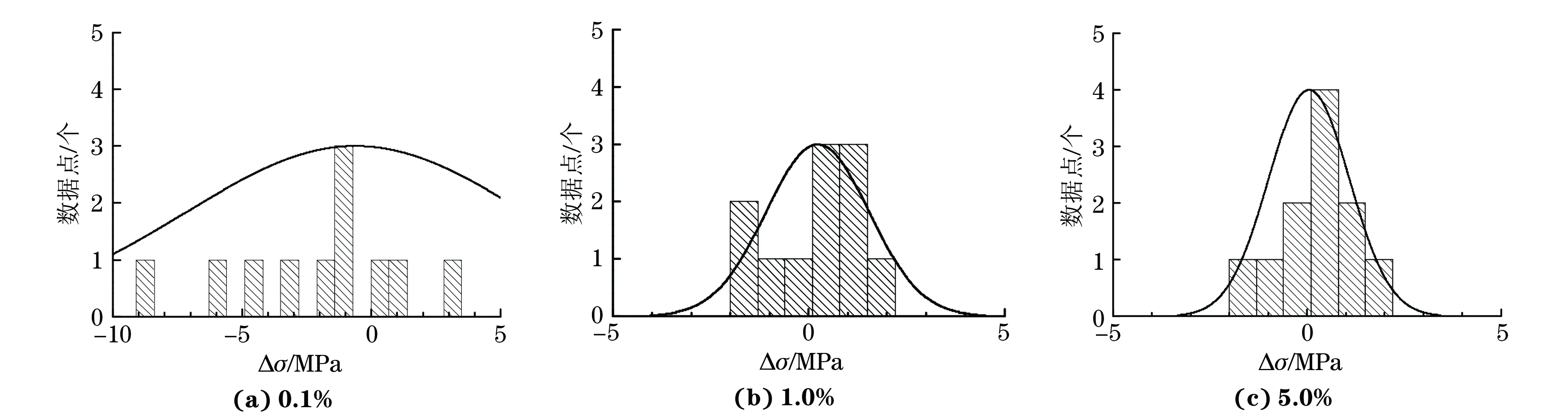
图5 不同蠕变应变下Δσ的概率密度分布Fig.5 Probability density distribution of Δσ at different creep strains

图3中(P，σ)数据点与其对应拟合曲线间的估计标准误差随蠕变应变的变化如图6所示，可见估计标准误差随蠕变应变的增加先迅速降低而后趋于平稳。这说明各数据点与回归拟合曲线的偏差程度逐步减小，即拟合曲线对数据样本的代表性越来越强。

综上所述，当在较大应变下进行寿命预测时，其寿命预测值与实测值比较接近，因此选定蠕变应变为5.0%进行进一步分析。

2.3 高温持久寿命预测和可靠性

根据材料性能数据的概率统计分布特性进行可靠性设计的思想已经体现在有关疲劳强度的设计中[11]；同样地，也可以通过分析持久性能数据的概率分布特性将可靠性设计思想引入到高温持久强度设计中。由图4得到蠕变应变为5.0%时的Zc，结合式(3)、式(2)可得到σ与P之间的关系。对高温蠕变数据进行统计，得到蠕变应变为5.0%时的分布参数，并结合σ与P的关系，对高温持久性能进行可靠性预测[9]，得到可靠性分别为80%，90%，95%的预测曲线，如图7中虚线所示。

由图7可以看出，当蠕变应变为5.0%时，基于Zc参数法预测得到的σ-P曲线与实际断裂时的曲线接近，实际断裂时(P，σ)数据点的离散程度较小，几乎全部落在可靠度为95%的曲线之上。

图7 由蠕变应变为5.0%时所得Zc预测得到的σ-P 曲线及其可靠性预测曲线Fig.7 Prediction curve for σ-P with Zc obtained at creep strain of 5.0% and the corresponding reliability prediction curves

图8 蠕变应变为5.0%时基于Zc得到的预测与实测 持久寿命之间的关系Fig.8 Relationship between prediction creep rupture life with Zc and experimental creep rupture life at creep strain of 5.0%

联立式(1)、式(2)和式(3)，并代入由图4得到的蠕变应变为5.0%时的Zc以及对应的试验温度和应力，预测得到试样的持久寿命；同时，还在其他温度和应力下进行了高温蠕变试验，得到了持久寿命并用Zc参数法预测这些温度和应力下的持久寿命。将预测得到的持久寿命和实测持久寿命作图，结果如图8所示，图中tp为预测持久寿命，tr为实测持久寿命。由图8可知，持久寿命预测结果大都分布在直线tr=tp上，且分布在[tr/2,2tr]之间，数据分散程度较小，预测结果很好。

3 结 论

(1) 引入参数P对不同蠕变应变下的温度和时间进行归一化处理，在此基础上，引入参数Zc对高温蠕变行为进行预测；随蠕变应变的增加，σ-P曲线趋近于断裂曲线，Zc呈现出先迅速增大后趋于稳定的变化趋势，(P，σ)数据点与其对应拟合曲线的偏差减小，数据的分散程度减小。

(2) 在蠕变应变为5.0%下，实测持久寿命几乎全部位于基于Zc参数法预测得到的σ-P曲线的可靠度为95%的曲线上，预测得到的持久寿命与实测持久寿命接近，数据分散程度较小，预测结果较准确。

参考文献：

[1] KINZOKU Z G K. NRIM creep data sheet[R]. Tokyo: National Research Institute for Metals, 1976.

[2] LARSON F R, MILLER J. A time temperature relationship for rupture and creep stress[J]. Transactions ASME, 1952,74(7): 765-775.

[3] EVANS R W, PARKER J D, WILSHIRE B. The θ projection concept: A model-based approach to design and life extension of engineering plant[J]. International Journal of Pressure Vessels and Piping, 1992, 50(1/2/2): 147-160.

[4] WILSHIRE B, SCHARNING P J. Creep ductilities of 9%-12% chromium steels[J]. Scripta Materialia, 2007, 56(12): 1023-1026.

[5] 蔡庆木, 刘月明, 黄昌清, 等. 火电厂高温压力管道寿命预测模型的可靠性及进展[J]. 机械工程材料, 2012, 36(12):5-9.

[6] TAMURA M, ABE F, SHIBA K, et al. Larson-Miller constant of heat-resistant steel[J]. Metallurgical and Materials Transactions A, 2013, 44(6): 2645-2661.

[7] KIM W G, YIN S N, KIM Y W, et al. Creep characterization of a Ni-based Hastelloy-X alloy by using theta projection method[J]. Engineering Fracture Mechanics, 2008, 75(17): 4985-4995.

[8] 江冯, 刘春慧, 程从前, 等. 采用不同方法预测10Cr9MoW2VNbBN钢蠕变曲线的比较[J]. 机械工程材料, 2015,39(3):89-93.

[9] 赵杰. 耐热钢持久性能的统计分析及可靠性预测[M]. 北京: 科学出版社, 2011.

[10] 冯炜. 基于Z参数的高温材料持久强度的可靠性分析[J]. 金属热处理, 2007,32(增刊1):469-472.

[11] 徐灏. 机械设计手册:第四卷[M]. 北京：机械工业出版社, 1991.