基于线性近似模型的三相不平衡有源配电网重构

吴在军, 成 晟, 朱承治, 徐俊俊, 周 力, 窦晓波

(1. 东南大学电气工程学院, 江苏省南京市 210096; 2. 国网浙江省电力有限公司, 浙江省杭州市 310007; 3. 国网苏州供电公司, 江苏省苏州市 215004)

0 引言

高渗透率光伏电站和风机等分布式电源(distributed generators,DG)的发电并网使得传统的单向辐射状配电网逐步转变为含多能源供电系统、必要时辅助以弱环状拓扑结构运行的有源配电网(active distribution network,ADN)[1-3]。DG强烈的间歇性、负荷的时变性及三相不平衡运行问题使得传统配电网重构策略面临严峻挑战[4-5]。

从数学角度分析,配电网重构是一个非线性、多约束、大规模的优化组合问题[6-8]。因此,降低重构模型寻优的复杂度及实现解的全局最优性是配电网重构亟需解决的关键问题。文献[9]以配电网最优有功网损为目标函数,建立了三相平衡网络重构数学模型,使用改进的禁忌搜索算法对模型进行求解,降低了算法对禁忌搜索步长的依赖程度,有效提升了重构问题的求解效率。文献[10]以线路损耗最低为目标,基于二阶锥形式的潮流方程建立了三相平衡配电网的重构模型,并使用变量转化等方法转换为凸优化模型,从而保证了优化结果的全局最优性。文献[11]通过将负荷转化为恒阻抗和恒电流的形式建立了三相平衡配电网二次规划模型,以网损最小和电压水平更优为目标函数,并使用商业求解器进行求解,从而保证了优化重构结果的拟全局最优性。文献[12]考虑了以网损最小为目标函数的三相不平衡配电网的重构问题,通过二阶锥松弛和big-M的方法将原非凸问题转化为混合整数二阶锥规划问题进行求解,保证了解的全局最优性。以上文献均可取得比较满意的结果,但只是基于单个时间断面的配电网运行状态进行静态重构研究,若将此种重构策略应用于实际工程,由于系统中各负荷和DG节点的注入功率具备时变特性,网络运行最优结构随时都需要调整,这不仅要求必须快速完成优化计算及网络重构过程以满足实时性要求,而且还需要快速频繁地操作开关,这无疑在经济和技术层面上都是不现实的[13-15]。

基于此考虑,开展计及DG和负荷注入功率间歇性、波动性的ADN重构方案,更具工程应用价值。文献[16]建立了以一天为期限的配电网重构模型,考虑了一天内的负荷动态变化特性及开关动作的费用,使用和声搜索算法和动态规划的方法对模型进行两阶段求解,最终得到一天内配电网开关动作顺序表。文献[17]提出基于信息熵时段划分的等效日负荷曲线分段方法,建立了以日损失费用最低为目标的ADN动态重构模型,使用改进杂草混合算法求解该模型,得到分时段重构策略。文献[18]提出了以网损和节点电压稳定性为目标函数的配电网动态重构,以负荷曲线的单调性和幅值变化大小为依据初步划分时间段落,综合考虑配电网网损最小和节点电压值最大且波动最小为目标寻找最佳开关动作策略,使用量子粒子群算法求解。以上文献的重构模型均考虑了一天内负荷或者DG的多时段变化特性,优化结果达到了预期目标,但是仍存在以下不足:①未考虑实际配电网三相不平衡运行的特点;②开关在一天内动作频率仍然较高,对系统运行冲击大,实际配电网一般以一天、一周或者季度作为重构周期[19];③普遍使用智能算法求解,难以保证解的全局最优性和唯一性,求解效率较低。

综上问题与研究,为考虑配电网的动态运行特性,本文基于对风力发电系统、光伏发电系统及负荷的日前预测曲线分析,提出以一天为开关动作周期的日重构决策方式,开关状态在重构周期内保持不变,以减少对系统运行的冲击。在此基础上,建立以配电网运行日损耗最低和电压偏差最小为总目标的三相不平衡ADN重构数学模型,并基于最佳等距分段线性逼近法对原非凸模型进行线性近似,在可控精度下提高问题的求解效率。最后采用标准化配电测试系统验证优化模型的有效性,并根据预先设置的最大逼近误差对线性近似方法的精确性进行分析。

1 DG与负荷日前预测模型

1.1 风力发电系统

风电机组一天内出力的间歇性主要由当地风速变化造成,研究表明Weibull分布是适应范围最广、拟合实际风速最好的模型[20],其概率密度函数为:

(1)

式中:v为风速;k和c分别为风电机组的形状参数和尺度参数。

易知风电机组的有功出力值与风速之间的函数关系为:

(2)

式中:Pr为风电机组的额定输出功率;vi,vr和vo分别为切入风速、额定风速和切出风速。

1.2 光伏发电系统

光伏发电系统有功出力易受当地光照强度影响,忽略逆变设备的损耗,光照强度可近似用Beta分布表示[15],其概率密度函数为:

(3)

式中:ζ和χ为Beta分布的形状参数,均大于0;e和eM分别为同一时段内的光照强度和光照强度最大值。

根据光照强度得到光伏发电有功出力PGM为:

(4)

式中:M为光伏电池板总数;Am和ηm分别为第m个电池板的面积和光电转换效率;A和η分别为电池板的总面积和光电转换效率。

对于风力和光伏发电机组的无功出力,假定通过风力和光伏机组中电容器的自动投切可使功率因数cosφ恒定不变[21],根据有功出力P得到风力与光伏发电机组的无功出力Q为:

(5)

1.3 常规负荷

为便于分析,假设待研究的配电网络各节点的负荷变化曲线是相同的,整个网络总的负荷曲线等于各节点的负荷曲线之和。本文选取文献[17]的等效日负荷曲线进行标幺化处理,选择系统给定的节点负荷功率作为基准,可以将得到的配电网络等效日负荷标幺化曲线转化为日负荷功率曲线。

2 三相不平衡ADN重构

2.1 日重构决策概述

配电网一般呈辐射状运行,且为了避免降低网络开关设备的工作寿命,通常以一天、一周或季度为最小动作周期进行网络重构[19]。本文以24 h为最小开关动作周期并等分为24个时段,以周期内总运行网损最低为目标,基于DG和负荷的日前预测曲线,配电网各时段的运行状况与各段起始时刻一致,在重构周期的0时刻之前确定周期内一组最优开关状态,计算优化后的下一日系统运行总网损。假设配电网络没有特定的初始拓扑,在重构决策生成之前,网络呈辐射状运行,并且系统的开关状态在24 h的周期结束之前都保持不变,即日重构决策在一天内开关仅动作一次。基于DG和负荷的日前预测曲线,可以计算系统一天的有功和无功动态潮流以得到最优的网络运行重构决策。ADN日重构的决策步骤示意图如图1所示。

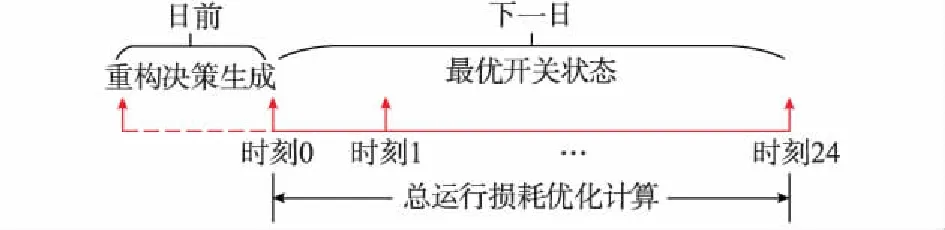
图1 日重构决策步骤示意图Fig.1 Schematic diagram of daily reconfiguration decision

相比于现有动态重构策略,本文所提ADN重构策略在重构的时间区间内将开关操作次数限制为1次,操作时刻限制在初始时刻,因此开关动作次数最少,对配电网运行的冲击也最小。另一方面,相比于传统静态重构,本文重构策略考虑了一天内配电网运行动态特性,在技术和经济层面上更符合实际应用。

2.2 三相Distflow潮流方程

由于ADN在重构前后都运行在辐射状网络状态,因此需要选择适用于辐射状配电网计算的潮流方程。本文基于具有递归特性的Distflow支路潮流方程组来描述辐射状网络中的潮流[22]。对于如图2所示的辐射状运行的ADN,为了体现重构问题中支路的开关状态可变的特点,其Distflow支路潮流方程形式如下。

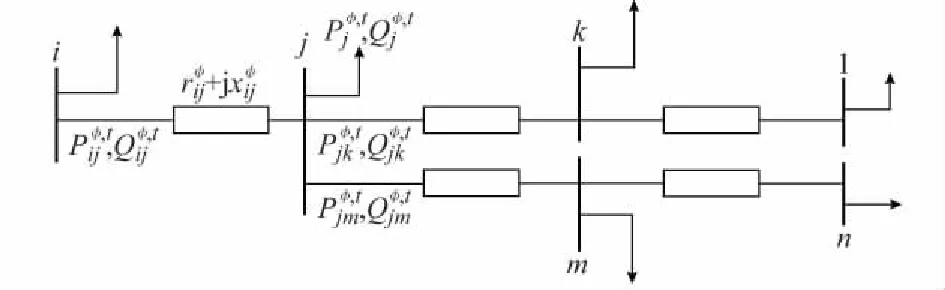
图2 辐射状配电线路示意图Fig.2 Topology of radial distribution network

对于时刻t线路中的节点j,有

(6)

对于时刻t支路ij,有

(7)

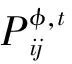
类似于前推回代法,根据Distflow潮流方程可以从支路的源节点向末节点一步一步计算,最终得到支路末端的潮流和节点电压,也可以反过来根据末端量回推到源节点的电压和支路潮流。

2.3 三相不平衡配电网重构数学模型

基于上述潮流模型,本文选择调度周期内配电网总的有功损耗最低和电压偏差最小作为目标函数建立三相不平衡配电网重构数学模型,总目标函数为:

(8)

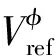
各时段具体的约束条件如下。

1)节点有功和无功功率注入平衡约束为式(6)。

2)支路电压潮流方程约束条件为式(7)。

3)配电网安全运行节点电压上下限约束条件为:

(9)

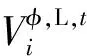
4)配电网安全运行支路功率上下限约束条件为:

(10)

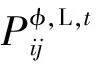
5)网络辐射状运行约束条件。辐射状配电网络与生成树具有十分相似的特性[23],结合该特性建立如下辐射状网络约束。

(11)

式中:βij为生成树的父子节点关系变量,当节点j是节点i的父节点时βij=1,反之取0;N(i)为跟节点i具有支路连接关系的节点集合。

其中第1行表明当支路ij连接时,必有一个节点是另一个节点的父节点;第2行则表明节点i只存在一个父节点;第3行表明源节点1不是任何节点的父节点。

2.4 重构模型的线性化与求解

由于上述三相不平衡配电网重构模型中存在双线性变量和二次约束,因此该模型是一个混合整数非凸非线性优化问题,尽管可以用非线性规划工具包,如内点法工具包进行求解,但难以保证其全局最优性。为提高ADN重构模型的求解效率,同时能够进一步确保线性化后模型的精确性,本文对所提重构模型采用如下所述的两阶段线性化方法。

1)二次项线性化

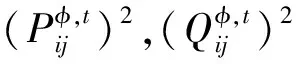
(12)

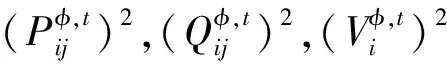
(13)

(14)

除此之外,对于各断面上线性函数的取值还需添加如下限制约束:

(15)

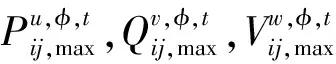
2)双线性项线性化

通过将上述二次项线性化处理,由于双线性项的存在重构模型仍是一个非线性问题,本文采用文献[23]的big-M方法进行处理,将三相不平衡配电网重构模型中的双线性项问题转化为线性问题。

至此,本文建立的三相不平衡ADN重构模型可以转化为混合整数线性规划模型,目标函数J等价的线性形式如下:

(16)

约束条件也均为线性条件,决策变量为配电网各开关状态和节点电压。利用商业求解器如Gurobi等可以对该线性规划问题进行有效求解。

3 算例测试与分析

3.1 改进IEEE 33节点配电网

1)算例介绍

本文首先采用如附录B图B1所示改进的IEEE 33节点三相不平衡配电网进行算例验证分析,该测试系统包含33个节点、37条支路,系统额定电压为12.66 kV、基准容量为10 MVA,多目标权重系数λ1和λ2分别为0.7和0.3。支路参数和负荷采用文献[25]的数据,并以各节点负荷功率作为功率基准,基于1.3节的日负荷标幺化曲线建立下一日的系统负荷曲线,系统总的有功和无功功率分别为3 635 kW和2 265 kvar。

变电站节点电压标幺值设置为1。DG预测采用1.1节与1.2节的数学模型,出力峰值为容量与功率因数的乘积,具体接入情况如附录B表B1所示。基于MATLAB R2017a仿真软件进行重构模型程序编写,在主频为3.5 GHz、内存为16 GB的计算机上,使用Gurobi商业求解器对混合整数线性规划模型进行求解。

2)仿真分析

为比较本文方法与不同算法的求解效果的差异,选取了粒子群算法[26]和二阶锥规划算法[12]与本文方法及遍历的结果对比,优化结果如表1所示。

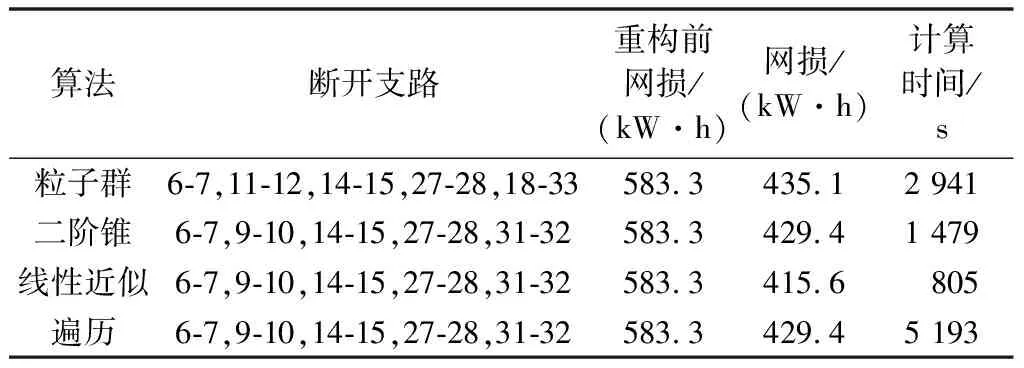
表1 改进IEEE 33节点配电网重构结果Table 1 Reconfiguration results of modified IEEE 33-bus distribution network

根据重构结果可知,二阶锥算法和本文的线性近似算法均可以准确获得网络重构的开关策略,即遍历算法所得到的结果。而采用文献[26]的粒子群算法所获得的结果虽然也能够大幅降低系统网损,但并非问题最优值。从计算效率来看,由于粒子群算法在进行求解过程中,需要频繁进行潮流计算,导致耗时最长,而二阶锥算法属于二次规划范畴,虽然能保证解的全局最优性,但是求解效率还是低于本文的线性规划模型。

重构后一天内不同时段A相的节点电压幅值如附录B图B2所示。夜间风电的接入使得电压水平较高,随着白天负荷的增加,网络节点电压的跌落幅度也随之增大,但是都在0.95～1.05(标幺值)安全运行范围内。此外,选择重构前后时刻12,A相的节点电压为例进行对比,如图3所示,可以看到重构后的电压偏差明显小于重构前节点电压,电压水平得到优化提升。

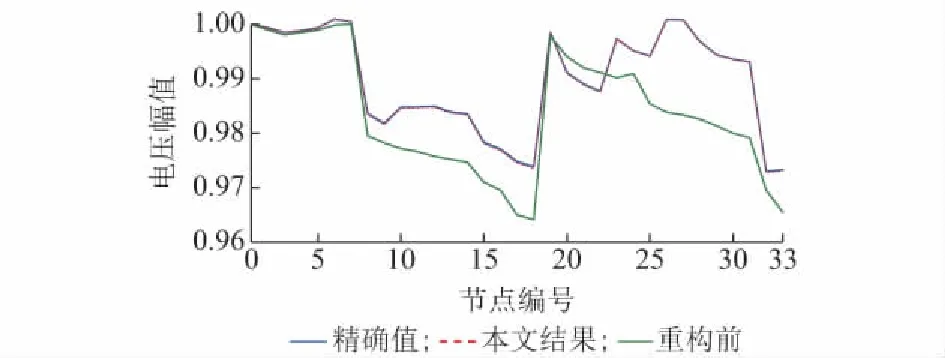
图3 节点电压对比Fig.3 Comparison of node voltage

需要提及的是,由于本文采用的线性化方法存在近似,导致优化的网损结果与精确值存在一定偏差,下面对该误差进行分析。定义时刻t支路有功功率和支路无功功率的线性化偏差如下:

(17)

本文预先设置支路有功功率和无功功率最佳等距线性化方法的最大逼近误差ε=0.001(标幺值),选择时刻12改进的IEEE 33节点配电网的支路有功功率线性化近似误差情况为例进行分析,如附录B图B3(a)所示。根据仿真结果,系统中所有支路有功功率线性化误差均小于ε,支路无功功率线性化误差结果与有功功率类似,且其他各时刻的功率误差均满足精度要求。

本文对支路电压潮流方程约束条件进行了线性化,因此优化结果的节点电压也存在一定误差。预先设置节点电压最佳等距线性化方法的最大逼近误差ε=0.001,类似于时刻t支路有功和无功偏差的定义,仍选择时刻12,A相的节点电压近似误差情况为例进行分析,如附录B图B3(b)所示,可以看到,在时刻12,该相的节点电压基本与精确值重合,并且系统所有节点电压误差均小于ε,且其他各时刻的各相电压误差均满足精度要求。

基于各时间断面数据进行传统动态重构,即一天内24个时刻均进行网络重构,将其结果与本文基于日重构决策的重构方法对比。根据仿真结果,本文只需要在日前进行1次开关状态的切换,对系统运行的冲击影响更小,有利于延长开关设备的使用寿命。而传统动态重构需要11次开关操作,网损方面的增长为9.8 kW·h,保持在可接受范围内。传统动态重构的详细开关动作情况如附录B表B2所示。

3.2 改进123节点配电网

1)算例介绍

为验证本文线性近似模型在较大系统中的准确性和有效性,使用如附录B图B4所示的123节点配电网进行算例验证。该系统包括123个节点,124条支路,系统的额定电压为4.16 kV,基准容量为10 MVA,多目标权重系数λ1和λ2分别为0.7和0.3。支路参数和负荷采用IEEE 123节点测试系统参数[27],并以其节点功率为基准,基于1.3节的日负荷标幺化曲线建立下一日的系统负荷曲线,系统总的额定有功和无功功率分别为3 490 kW和1 925 kvar。

变电站节点电压标幺值设置为1。DG预测采用1.1节与1.2节的数学模型,出力峰值为容量与功率因数的乘积,具体接入情况如附录B表B3所示。基于MATLAB R2017a仿真软件进行重构模型程序编写,在主频为3.5 GHz、内存为16 GB的计算机上,使用Gurobi商业求解器对模型进行求解。

2)仿真分析

由于改进123节点测试系统存在124条支路,组合遍历的求解计算量过大,因此仅比较各类算法求解结果优劣,优化结果如表2所示。

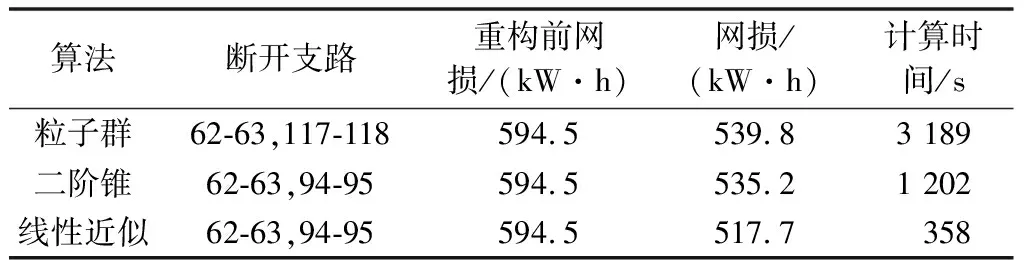
表2 改进的123节点配电网重构结果Table 2 Reconfiguration results of modified 123-bus distribution network

根据重构结果可知,本文的线性近似算法与二阶锥模型获得的重构开关策略相同,由于二阶锥模型与粒子群算法不存在近似过程,因此可认为优化网损即为实际网损,采用文献[26]的粒子群算法所获得的结果虽然也能够大幅降低系统网损,但并非最优。从计算效率来看,由于粒子群算法在进行求解过程中,需要频繁进行潮流计算,导致耗时最长,大于33节点系统所耗时间。二阶锥算法与线性近似算法均属于数学规划算法,无须反复进行潮流计算,算法复杂度主要跟联络开关数量有关。可以看到,尽管网络规模增加但由于联络开关较少,线性近似算法仍能保持高效率;二阶锥算法属于二次规划范畴,虽然能保证解的全局最优性,但是求解效率仍然不高。本文线性近似模型能够在得到最优重构策略的同时保证高效的求解效率。

重构后24个时段内本文重构方案的A相节点电压幅值如附录B图B5所示。夜间风电的接入使得电压水平较白天更优,随着白天负荷的增加,网络节点电压的跌落幅度也随之增大,但都在0.95～1.05(标幺值)安全运行范围内。另一方面,选择重构前后时刻12,A相的节点电压为例进行对比,如图4所示,重构后的电压偏差明显小于重构前节点电压,电压水平得到有效提升。

预先设置的支路有功和无功功率最佳等距线性化方法最大逼近误差ε=0.001,选择时刻12,对部分35至60节点的有功功率线性化近似误差情况为例进行分析,如附录B图B6(a)所示。可以看到,系统中支路有功功率线性化误差均小于ε,支路无功功率线性化误差结果与有功功率类似,且其他各时刻的各相功率误差均满足精度要求。

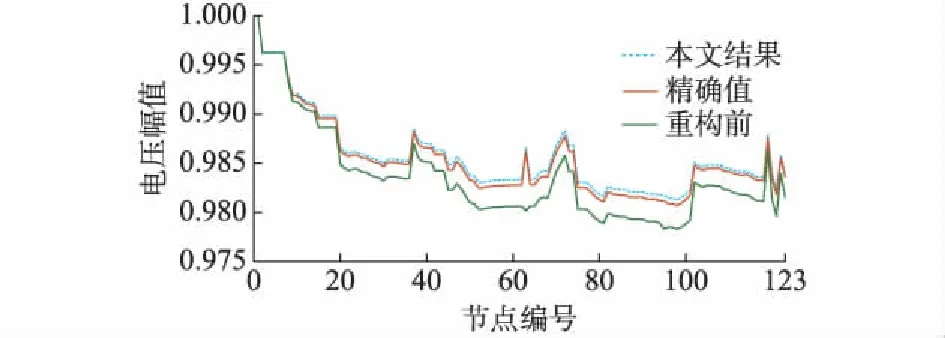
图4 节点电压对比Fig.4 Comparison of node voltage

接下来对优化结果的节点电压误差进行分析。本文预先设置节点电压最佳等距线性化方法的最大逼近误差ε=0.001,仍选择时刻12,A相的节点35至60电压误差情况为例,如附录B图B6(b)所示,在时刻12时,该相的系统所有节点电压误差均小于ε,且其他各时刻的各相电压误差均满足精度要求。

基于各时间断面数据进行传统动态重构,即一天内24个时刻均进行网络重构,将其结果与本文基于日重构决策的重构方法对比,本文方法对系统运行的冲击影响更小,有利于延长开关设备的使用寿命,而传统动态重构需要7次开关操作。网损方面的增长为3.9 kW·h,在可接受范围内。传统动态重构的详细开关动作情况如附录B表B4所示。

4 结语

本文首先对DG出力和节点负荷进行日前短期预测,提出以一天为开关动作周期的日重构决策方式,考虑了配电网运行动态特性,开关状态在重构周期内保持不变。相比于现有动态重构策略,本文重构策略的开关动作次数最少,对配电网运行的冲击也最小;相比于静态重构,本文根据一天内配电网负荷和DG运行的动态特性制定重构方案,在技术和经济层面上更符合实际应用。

以下一日总网损最低为目标函数,加以系统安全稳定运行的约束,建立了基于日重构决策的三相不平衡配电网优化重构模型,并且使用最佳等距分段线性逼近法对原非线性模型实现精度可控的线性逼近。基于改进的33节点和123节点配电网,通过多种方法的对比分析,验证了本文模型的有效性,并且对支路功率和节点电压的线性近似程度进行了误差分析,在保证求解精度的同时实现问题的高效求解。

目前对于三相不平衡配电网的重构研究仅考虑确定的DG出力和负荷功率,未考虑可能存在的不确定性因素对于动态重构的影响。今后可在此研究基础上将DG和负荷的不确定性纳入重构技术,提高配电网重构技术在线应用的适应能力。另一方面,未来配电网运行状态复杂多变,需要结合实际运行特性进一步研究更合理的重构周期。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 陈旭,张勇军,黄向敏.主动配电网背景下无功电压控制方法综述[J].电力系统自动化,2016,40(1):143-151.DOI:10.7500/AEPS20150330005.

CHEN Xu, ZHANG Yongjun, HUANG Xiangmin, et al. Review of reactive and voltage control method in the background of active distribution network[J]. Automation of Electric Power Systems, 2016, 40(1): 143-151. DOI: 10.7500/AEPS20150330005.

[2] 刘东,陈云辉,黄玉辉,等.主动配电网的分层能量管理与协调控制[J].中国电机工程学报,2014,34(31):5500-5506.

LIU Dong, CHEN Yunhui, HUANG Yuhui, et al. Hierarchical energy management and coordination control of active distribution network[J]. Proceedings of the CSEE, 2014, 34(31): 5500-5506.

[3] WANG C, YU H, LI P, et al. EMTP-type program realization of Krylov subspace based model reduction methods for large-scale active distribution network[J]. CSEE Journal of Power & Energy Systems, 2015, 1(1): 52-60.

[4] 李传健,刘前进.考虑风力发电随机性的配电网重构[J].电力系统自动化,2010,34(20):34-39.

LI Chuanjian, LIU Qianjin. Distribution network reconfiguration considering randomness of wind power generation[J]. Automation of Electric Power Systems, 2010, 34(20): 34-39.

[5] 吴泓俭,雷霞,刘斌,等.基于遗传膜算法的含风电机组和电动汽车的配电网分时段动态重构[J].电工技术学报,2016,31(2):196-205.

WU Hongjian, LEI Xia, LIU Bin, et al. Membrane computing based genetic algorithm for dynamic reconfiguration of distribution network with dividing time and considering electric vehicles and wind turbines[J]. Transactions of China Electrotechnical Society, 2016, 31(2): 197-205.

[6] 徐成司,董树锋,孙洲,等.基于网络简化和深度优先遍历的配电网路径搜索算法[J].电力系统自动化,2017,41(20):1-7.DOI:10.7500/AEPS20170605015.

XU Chengsi, DONG Shufeng, SUN Zhou, et al. A path searching algorithm for distribution network based on network simplification and depth first traverse[J]. Automation of Electric Power Systems, 2017, 41(20): 1-7. DOI: 10.7500/AEPS20170605015.

[7] 王倩.含分布式电源的配电网重构[D].北京:华北电力大学,2012.

[8] 朱正,廖清芬,刘涤尘,等.考虑新能源与电动汽车接入下的主动配电网重构策略[J].电力系统自动化,2015,39(14):82-88.DOI:10.7500/AEPS20141217002.

ZHU Zheng, LIAO Qingfen, LIU Dichen, et al. Strategy of distribution network reconfiguration considering wind power and electric vehicle integration[J]. Automation of Electric Power Systems, 2015, 39(14): 82-88. DOI: 10.7500/AEPS20141217002.

[9] ZHANG Dong, FU Zhengcai, ZHANG Liuchun. An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems[J]. Electric Power Systems Research, 2007, 7(7): 685-694.

[10] RABIH A, RAVINDRA S, BIKASH C. Minimum loss network reconfiguration using mixed-integer convex programming[J]. IEEE Transactions on Power System, 2012, 27(2): 2666-2675.

[11] HAMED A, JOSE R. Distribution system optimization based on a linear power-flow formulation[J]. IEEE Transactions on Power Delivery, 2015, 30(1): 25-33.

[12] TIAN Zhuang, WU Wenchuan, ZHANG Boming, et al. Mixed-integer second-order cone programing model for VAR optimisation and network reconfiguration in active distribution networks[J]. IET Generation, Transmission & Distribution, 2016, 10(8): 1106-1115.

[13] 江东林,刘天琪,李樊.采用时段动态划分和分层优化策略的配电网重构[J].电网技术,2012,36(2):153-157.

JIANG Donglin, LIU Tianqi, LI Fan. Dynamic distribution network reconfiguration based on dynamic partition of time intervals and hierarchical optimization[J]. Power System Technology, 2012, 36(2): 153-157.

[14] 刘蔚,韩祯祥.基于时间区间的配电网重构[J].电力系统自动化,2006,30(10):33-38.

LIU Wei, HAN Zhenxiang. Distribution system reconfiguration based on time interval[J]. Automation of Electric Power Systems, 2006, 30(10): 33-38.

[15] 易海川,张彼德,王海颖,等.提高DG接纳能力的配电网动态重构方法[J].电网技术,2016,40(5):1431-1436.

YI Haichuan, ZHANG Bide, WANG Haiying, et al. Distribution network dynamic reconfiguration method for improving distribution network’s ability of accepting DG[J]. Power System Technology, 2016, 40(5): 1431-1436.

[16] MOHAMMAD H, MAHMOUD R, JAVAD S, et al. Duration based reconfiguration of electric distribution networks using dynamic programming and harmony search algorithm[J]. Electrical Power and Energy Systems, 2012, 1(10): 21-29.

[17] 赵静翔,牛焕娜,王钰竹.基于信息熵时段划分的主动配电网动态重构[J].电网技术,2017,41(2):402-408.

ZHAO Jingxiang, NIU Huanna, WANG Yuzhu. Dynamic reconfiguration of active distribution network based on information entropy of time intervals[J]. Power System Technology, 2017, 41(2): 402-408.

[18] 文娟,谭阳红,雷可君.基于量子粒子群算法多目标优化的配电网动态重构[J].电力系统保护与控制,2015,43(16):73-78.

WEN Juan, TAN Yanghong, LEI Kejun. Multi-objective optimization of distribution network dynamic reconfiguration based on integer coded quantum particle swarm optimization algorithm[J]. Power System Protection and Control, 2015, 43(16): 73-78.

[19] HAGHIGHAT H, ZENG B. Distribution system reconfiguration under uncertain load and renewable generation[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2666-2675.

[20] 赵俊华,文福拴,薛禹胜,等.计及电动汽车和风电出力不确定性的随机经济调度[J].电力系统自动化,2010,34(20):22-29.

ZHAO Junhua, WEN Fushuan, XUE Yusheng, et al. Power system stochastic economic dispatch considering uncertain outputs from plug-in electric vehicles and wind generators[J]. Automation of Electric Power Systems, 2010, 34(20): 22-29.

[21] 王成山,郑海峰,谢莹华,等.计及分布式发电的配电系统随机潮流计算[J].电力系统自动化,2005,29(24):39-44.

WANG Chengshan, ZHENG Haifeng, XIE Yinghua, et al. Probabilistic power flow containing distributed generation in distribution system[J]. Automation of Electric Power Systems, 2005, 29(24): 39-44.

[22] MESUT E, FELIX F. Network reconfiguration in distribution system for loss reduction and load balancing[J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.

[23] JOSHUA A, FRANZ S. Convex models of distribution system reconfiguration[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1407-1413.

[24] 王少军,张启荣,彭宇,等.超越函数FPGA计算的最佳等距分段线性逼近方法[J].仪器仪表学报,2014,35(6):1209-1216.

WANG Shaojun, ZHANG Qirong, PENG Yu, et al. Optimal equidistant piecewise linear approximation algorithm for the computation of transcendental functions in FPGA[J]. Chinese Journal of Scientific Instrument, 2014, 35(6): 1209-1216.

[25] 车仁飞,李仁俊.一种少环配电网三相潮流计算新方法[J].中国电机工程学报,2003,23(1):74-79.

CHE Renfei, LI Renjun. A new three-phase power flow methed for weakly meshed distribution systems[J]. Proceedings of the CSEE, 2003, 23(1): 74-79.

[26] 赵晶晶,李新,彭怡,等.基于粒子群优化算法的配电网重构和分布式电源注入功率综合优化算法[J].电网技术,2009,33(17):162-166.

ZHAO Jingjing, LI Xin, PENG Yi, et al. A comprehensive optimization algorithm for injection power of distributed generation and distribution network reconfiguration based on particle swarm optimization[J]. Power System Technology, 2009, 33(17):162-166.

[27] IEEE PES Distribution Test Feeders. IEEE 123 node test feeder[EB/OL]. [2018-01-08]. http://www.ewh.ieee.org/soc/pes/dsacom/testfeeders/.