模块化五电平逆变器子模块开路故障的智能诊断方法

尹桥宣, 段 斌, 沈梦君, 屈相帅

(1. 智能计算与信息处理教育部重点实验室, 湘潭大学, 湖南省湘潭市 411105;2. 湖南省风电装备与电能变换协同创新中心, 湘潭大学, 湖南省湘潭市 411105)

0 引言

模块化多电平变换器(modular multilevel converter,MMC)作为一种新型的柔性一次设备[1],已被广泛应用在电力系统中,显著提升了电能的转换和传输效率,增强了电力系统的调控能力与灵活性[2-3]。MMC的子模块(sub-module,SM)含有大量的功率器件,使得MMC每个子模块都是潜在故障点[4-5]。为了保护子模块电路,减少子模块故障的影响,一些驱动保护电路已被集成到子模块控制器上,如过热、过流、过载继电器[6-8]。但这些保护电路设计复杂且诊断能力较弱,无法识别出某些故障类型,使得保护容易失效[8]。因此,研究一种高效的故障诊断方法对MMC稳定运行至关重要。

近年来,国内外针对多电平逆变器故障诊断的方法大致可划分为3类:①基于数学模型的方法[9];②基于信号处理的方法[10-11];③基于知识的方法[12-13]。基于数学模型的方法,需要构建准确的数学模型进行故障类型识别,而多电平逆变器属于高阶、非线性、强耦合系统,难以构建出准确的数学模型,故基于数学模型的故障诊断方法应用于多电平逆变器存在局限性[14]。基于信号处理的方法主要有基于频谱分析和基于小波变换两种方法：基于频谱分析的方法主要将采集到的信号从时域变换到频域上,提取故障波形的频谱特征,实现故障诊断[15]；而基于小波变换的方法具有良好的时频局部化特性,能够有效地提取故障特征,与其他方法相结合能够完成各种故障诊断任务[16]。尽管这些方法已应用于多电平逆变器故障诊断中,但它们需要许多与特定系统配置相关的先验知识,而且确定实现过程需要不断调整。因此,基于信号处理的方法可能相当耗时且缺乏通用性。基于知识的方法通常先对采样数据进行特征提取,然后利用决策树、神经网络、支持向量机等分类器[17-18]进行故障分类识别。而特征提取过程作为关键步骤,通常很耗时且需要大量的带标签数据获取先验知识,而且特征大多数是手动设计,很难获得故障数据的深层次特征。

深度学习作为机器学习领域的一种新兴方法,以其强大的自动特征提取能力在图像识别、语音识别等领域已取得了显著的成果[19-21]。在深度学习模型中,栈式稀疏自动编码器(stacked sparse auto-encoder,SSAE)作为无监督学习网络,能在有标记数据有限的情况下进行特征学习,而且整体性能要优于卷积神经网络、深度信念网络等模型[21]。因此,本文提出了一种基于SSAE的模块化五电平逆变器(modular five-level inverter,MFLI)子模块开路故障诊断方法。该方法将故障检测与定位问题转化为深度学习擅长的分类问题,利用SSAE进行无监督特征学习,构建原始故障数据的深层特征表达,最后将深层特征连接到Softmax分类器输出故障诊断结果。因此,本文所提出的方法具有如下2个优点:①传统方法耗时的手工特征设计过程被自动特征学习过程替代;②通过无监督特征学习充分利用MFLI在线监测设备收集的大量未标记数据。此外,为了提高该方法的抗噪性能,利用已添加高斯白噪声的数据对SSAE进行训练,以提高其特征表达鲁棒性。

1 MFLI工作原理及故障分析

1.1 MFLI拓扑结构

MFLI基本拓扑结构[22]如图1所示,共有6个桥臂,每个桥臂由4个子模块和1个电抗器(L0)串联而成,每相单元由上桥臂和下桥臂组成。其中每个子模块包括2个IGBT器件T1和T2、2个反并联二极管D1和D2,以及1个直流侧电容器CSM。图中:iarm为子模块输入电流;USM为子模块输出电压;UC为子模块的电容电压;各物理量的参考方向如图1所示。

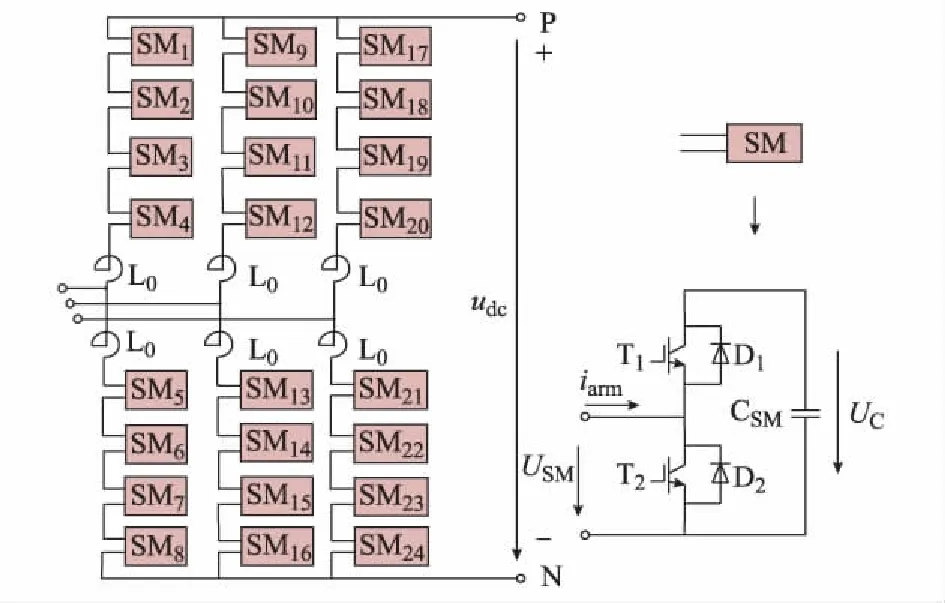
图1 MFLI电路拓扑结构Fig.1 Topology structure of MFLI circuit

1.2 子模块故障特性

MFLI子模块故障通常分为2种类型[23]:短路故障和开路故障。短路故障破坏性较大,因而子模块驱动电路中一般配备了短路保护模块,当短路故障发生时,由本地闭锁该子模块,确保系统仍可正常运行。开路故障危害相对较小,因而不易被立即检测到,从而造成电压电流波形畸变等后果,威胁到系统的正常运行[6-8,24]。因此,本文主要研究子模块中绝缘栅双极型晶体管(IGBT)器件的开路故障,包括T1开路故障、T2开路故障、T1和T2同时开路故障3种类型。子模块开路故障后桥臂电流的正负所对应的子模块输出电压特性与子模块正常运行时有所不同[23],具体区别如下。

1)类型Ⅰ:T1开路故障,如图2(a)所示。对于投入状态下的子模块,当iarm>0时电流流经D1和CSM,电容仍可正常充电,子模块输出电压为UC。但当iarm<0时,电流被迫流经D2,此时电容无法正常放电,子模块输出电压USM=0,与正常状态不同。对于切除状态下的子模块,其运行情况与正常时一致。

2)类型Ⅱ:T2开路故障,如图2(b)所示。对于切除状态下的子模块,当iarm>0时电流流经D1和CSM,电容被充电,子模块输出电压USM=UC,不同于正常状态下的USM=0。其他情况均与正常时一致。

3)类型Ⅲ:T1和T2同时开路故障。类型Ⅲ的故障特性同时包含了类型Ⅰ和类型Ⅱ的故障特性,即在子模块处于投入状态且iarm<0和子模块处于切除状态且iarm>0这两种情况下,电流iarm的流向与子模块输出电压USM的值均与正常状态时不同。

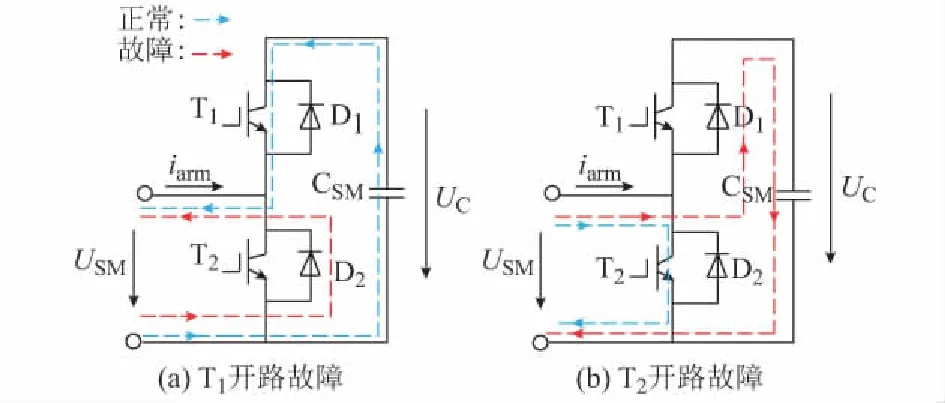
图2 子模块开路故障Fig.2 Open-circuit fault for SMs

由以上分析可知,T1和T2开路故障会导致电容异常充放电,因此在子模块出现开路故障时电容电压会出现波动。现有子模块开路故障检测与定位的方法主要采用人工比较子模块电容电压的方法,即通过计算故障子模块电容电压与正常运行子模块电容电压之间差值实现故障检测与定位[1,6-7]。这类方法不仅需要花费一定的计算时间,而且当桥臂电流很小时,故障子模块电容电压与正常运行子模块电容电压的差值也会很小,故障特征不够明显,使得故障检测与定位工作变得很难。本文将MFLI中子模块电容电压信号组合成24通道序列信号,利用SSAE以无监督方式从中自动提取数量最少且拟合最好的深层次特征信息,减少故障诊断中人工特征提取的工作量,提高故障诊断效率。

2 基于SSAE的MFLI故障诊断方法

2.1 SSAE

自动编码器(auto-encoder,AE)是一种由输入层、隐含层和输出层组成的3层神经网络[25-27],其结构具有对称性,如图3所示。AE通过隐含层对输入数据进行编码,然后由重构输入数据得到输出。通过使重构误差最小,获得最佳的数据隐含层表达。稀疏自动编码器(sparse auto-encoder,SAE)主要在AE的损失函数上添加稀疏约束项,以提高其特征学习能力[25-26]。由于SAE的构造能力有限,所以为了构成表达能力更强的函数,通常将多个SAE依次堆叠构成深度网络结构,即SSAE[27-28]。在SSAE网络结构中,前一个SAE的隐含层输出作为后一个SAE的输入。根据后文3.3节可知,本文所提出的故障诊断模型采用由2层SAE构成的SSAE,即由1个输入层、2个隐含层和1个输出层构成,其结构见附录A图A1。

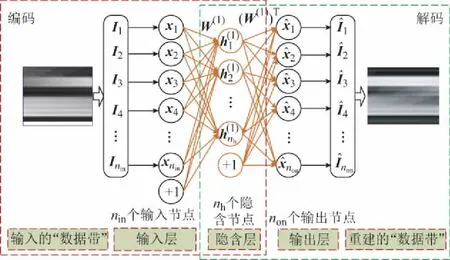
图3 AE结构Fig.3 Architecture of AE

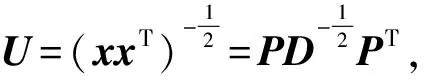
xZCA=Ux

(1)

为便于表示,文中继续使用x表示经过预处理的输入数据xZCA,依次执行编码和解码过程。

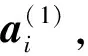
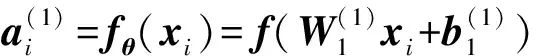
(2)

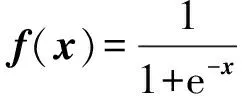
(3)

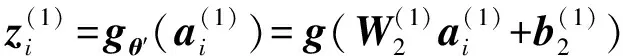
(4)

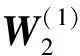
则第1层SAE的损失函数为:

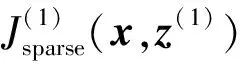
(5)

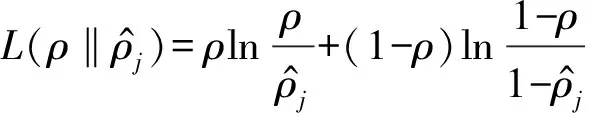
(6)

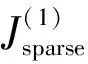
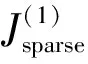
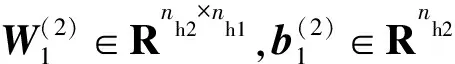
(7)

SSAE的训练过程由无监督预训练和有监督微调2个阶段构成。在预训练阶段,逐层训练每个SAE,得到原始输入的深度特征表达,由此避免传统深度结构容易陷入局部极小值的问题。在微调阶段,将SSAE的所有层作为一个整体来构建代价函数,利用BP算法调整所有层的权值参数,经过微调后的故障诊断的准确度和泛化能力可显著提高。

2.2 Softmax分类器

本文将MFLI子模块开路故障诊断问题转化为分类问题,通过Softmax分类器[28]的输出来判断是否发生故障及故障发生的位置。具体地,将MFLI中24个子模块按照从A相到C相,每相中从上臂到下臂的顺序依次标记为1到24。从子模块故障发生前采样到的样本标记为“正常”,标签为0;从故障发生后采样到的样本标记为“故障”,标签为发生故障的子模块的标号,即1到24中的某个数。把“正常”和24个不同子模块发生“故障”定义为不同的类别,则一共有25种样本类别。因此,只需通过Softmax分类器预测出“数据带”样本的类别,就能判断MFLI中是否有子模块发生故障并确定是哪一个子模块发生故障(即故障位置)。

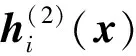
(8)

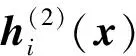
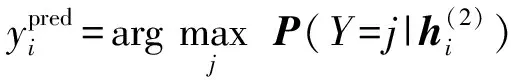
(9)

Softmax分类器的损失函数为:

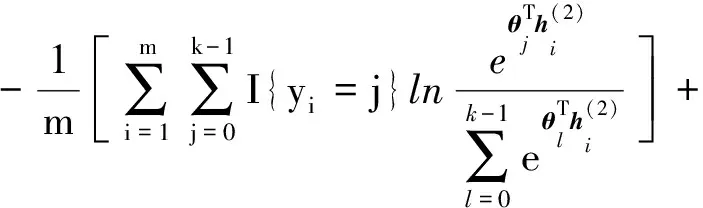
(10)

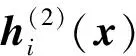
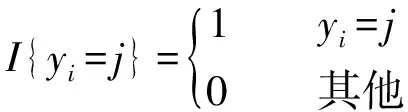
(11)

利用L-BFGS-B优化算法训练Softmax分类器,以最小化损失函数Js(θ)为目标,训练得到最优的参数θ∈Rk×nh2,将参数θ重塑成W(3)∈Rnh2×k。

2.3 基于SSAE的MFLI故障诊断流程

基于SSAE的MFLI子模块开路故障诊断的具体步骤如下。

步骤1:选取MFLI中的24个子模块电容电压信号组合成24通道序列,按照min-max方式对24通道序列信号进行归一化处理。

步骤2:利用大小为24lwindow(lwindow为窗口长度)的滑动窗口按时间顺序等间隔切割24通道序列信号,获得“数据带”样本,即灰度图。将所有24通道序列信号切割获得的灰度图合并成一个样本集,并按照一定比例划分为训练样本集和测试样本集。

步骤3:使用训练样本集训练SSAE网络模型和Softmax分类器,获得最佳参数,得到故障诊断模型。

步骤4:将测试样本集输入已训练好的故障诊断模型进行故障诊断。

3 模型参数调整与分析

3.1 MFLI仿真系统搭建和实验数据获取

为验证所提故障诊断方法的可行性,本文按照图1的MFLI拓扑结构在PSCAD/EMTDC软件环境下搭建仿真系统,系统频率50 Hz,系统容量5.5 MVA,直流侧电压10 kV。通过改变附录A表A1所示的系统参数生成由子模块电容信号组成的24通道序列信号数据集,并尝试所有参数的组合,共收集864个24通道序列信号数据样本。MFLI仿真系统在2.0 s处发生故障,并以20 kHz的采样频率采集0～4 s时间范围内24个子模块电容电压信号,构成24通道序列信号。SM1三种开路故障仿真波形见附录A图A2。为了开展后续基于SSAE的故障诊断实验,首先对24通道序列信号进行归一化预处理,然后利用大小为24lwindow的滑动窗口在每个24通道序列中按时间顺序等间隔采样n个“数据带”样本,最后根据实验需要设置n和lwindow。

在SSAE模型参数调整和分析实验中,窗口长度lwindow和每个24通道序列信号采样样本数量n分别设置为40和100。由于数据带的大小为24×40,因此模型的输入层节点数为960,而“正常”和24个不同子模块共有25种样本类别,则输出层节点数为25。在故障诊断模型中,SAE的权重衰减参数λ设为0.003,稀疏惩罚项权重系数β设为3,Softmax分类器的代价函数中的权重衰减参数λs的值设为0.000 1,模型训练时迭代次数设为400。每个子模块随机抽取6个24通道序列样本,即共144个24通道序列样本,获得一个含有14 400个“数据带”样本的数据集,把该数据集随机划分为10 080个“数据带”样本(即数据集的70%)作为训练集,4 320个“数据带”样本(即数据集的30%)作为测试集进行本节实验,讨论分析故障参数对故障诊断实验效果的影响。

3.2 隐含层神经元数对模型效果的影响

当隐含层神经元的数量较少时,所学习到的特征有限,容易导致模型的特征表达能力不足。反之,又容易导致模型过拟合。通过10折交叉验证法和网格搜索自动调参方法进行相关实验,讨论隐含层神经元数量对故障诊断结果的影响。附录A图A3为当稀疏参数ρ=0.2时SSAE的2个隐含层在不同神经元数目下的测试结果图。由图A3可知,故障诊断准确度会随着神经元数目的增加而增加,而当2个隐含层的神经元数目均为120时实验结果最好,达到97.13%。此外,从图A3中可以看出,隐含层节点数越多时,故障诊断准确度不一定越高,过多的节点数可能会导致SSAE过拟合。

3.3 隐含层数量对模型效果的影响

随着隐含层数量的增加,模型能学习更高层、更抽象的数据特征表示,但隐含层数量过多时又容易导致模型过拟合,因此有必要讨论隐含层数量对故障诊断效果的影响。本文设置SSAE中隐含层的数量分别为{1,2,3},隐含层神经元数分别为{150,120,100,90},且各层神经元数量保持一致,设置稀疏参数ρ=0.2。不同隐含层数量对应的故障诊断实验结果见附录A图A4。从图A4中可以看出,当隐含层数量为2时,实验结果最好,故障诊断准确度为97.13%。当隐含层数量为3时,故障诊断准确度明显下降,说明此时SSAE出现过拟合。由以上分析可知,隐含层数量设置得过大或者过小都会导致故障诊断准确度降低。

3.4 稀疏参数对模型效果的影响

SAE的核心思想是把所有隐含层神经元的平均激活水平限制在较小的范围内,但对于它的稀疏性参数的选择没有给出明确的指示。本文通过10折交叉验证法确定稀疏参数ρ范围为[Smin,Smax]。为了满足稀疏条件,Smax的值选择不能过大。同时,Smin的值也不能过小,否则所有隐含的节点都不能被有效地激活,也会降低特征提取的效率。不同稀疏参数下故障诊断准确度的误差见附录A图A5,结果表明,对于给定的数据集,当稀疏参数设定在[0.15,0.35]之间时,整体故障诊断精度达到96%以上;当参数取得过小,如稀疏参数ρ=0.05时,故障诊断准确度下降到88.15%。而当参数值达到0.4以上时,故障诊断精度会迅速下降,误差大大增加。因此,在本文实验中,稀疏参数会在[0.15,0.35]之间选择。其中ρ=0.2时,实验结果最好,达到97.13%。

4 实验结果分析

4.1 实验结果

从3.1节获得的数据集中为每个子模块随机抽取4个24通道序列信号样本,即共96个24通道序列样本,按照同样的方式生成含有9 600个“数据带”样本的数据集,对完成参数调试的模型进行验证。附录A图A6是当2个隐含层的神经元数目都为120且ρ=0.2时,其故障诊断准确度所对应的混淆矩阵。混淆矩阵的行对应样本所属的真实类别,列对应模型给出样本的预测类别。

从附录A图A6中可以看出,故障诊断精度较高,经计算可得平均正确率为98.09%。出现错误的故障诊断主要是因为MFLI仿真系统中子模块由正常状态突变为故障状态后,电容电压不会立即突变,而是随着充放电过程逐渐发生变化,导致在故障时刻点前后采样到的正常样本和故障样本之间相似性高,容易混淆,导致故障检测与定位出现误差。实验结果表明,基于SSAE的MFLI故障诊断模型能够以很高的准确度完成故障诊断。

4.2 故障诊断时间

为获取故障诊断时间,从3.1节获得的数据集中为每个子模块随机抽取3个24通道信号样本,共72个24通道信号样本,绘制每个信号样本的模型输出。由于本文MFLI仿真实验设定子模块开路故障开始时间为第2 s,因此在24通道序列的1.9～2.4 s时间段内,利用滑动窗口以1 ms的步长从左向右移动,获得500个大小为24×40的“数据带”样本,作为训练好的模型输入,获得故障诊断模型的预测输出并进行滤波操作,最后绘制出每个“数据带”样本的模型输出,如附录A图A7所示。具体地,在检测到故障前,每个“数据带”样本的模型输出为0,即“无故障”类别。当检测到子模块故障后,模型的输出为故障子模块的标号,即1～24之间的某个数。为清楚显示每个“数据带”样本对应的模型输出,在原始输出上添加了一个服从正态分布N(0,0.1)的常数,将所有输出稍微向上或向下移动。本文对各子模块的故障检测时间进行了统计,见附录A图A8。最快检测时间为13 ms,最慢检测时间为52 ms,平均检测时间为31.47 ms。相比于文献[31]利用子模块电容电压值比较的方法定位子模块,故障诊断时间为100 ms,本文具有一定优势。

4.3 对比结果

将本文提出的基于SSAE的故障诊断模型与反向传播神经网络(BPNN)和支持向量机(SVM)等两种方法进行比较分析,其中BPNN输入层节点数为960,2个隐含层节点数分别为512和128,输出层节点数为25。SVM采用“一对多”法实现多值分类,设定径向基函数(RBF)核函数惩罚项参数C=1,核系数γ=0.02,实验得到SSAE,SVM,BPNN的正确率分别为98.09%,86.78%,93.67%。可见,本文方法比其他方法的实验结果在诊断上具有一定的优势。

4.4 抗噪性能

为确保所提出的故障检测与定位方法能够在数据存在噪声和测量误差的情况下仍具有较好的性能,同时验证特征提取过程的泛化性,本文向训练集数据样本添加不同强度的高斯白噪声,对SSAE进行训练,以提高其特征表达的鲁棒性,实验结果如下:噪声强度分别为5%,10%,15%,20%,25%时,正确率分别为96.71%,95.93%,93.84%,93.29%,91.71%。可以看出,当噪声的强度为25%时,故障诊断准确度仍能达到91.71%,说明该方法的抗噪性能较好。

5 结语

在MFLI发生子模块故障后及时完成故障检测与定位,并结合相应的保护策略保障MFLI的正常运行,这一工作具有一定的工程应用价值和现实意义。本文将深度学习技术应用于MFLI故障诊断领域,把故障诊断问题转换成深度学习模型所擅长的分类问题,将MFLI子模块电容电压信号组成24通道序列信号,并沿24通道序列信号移动大小为24×40的采样窗口获得“数据带”样本。然后利用SSAE对“数据带”样本进行无监督学习,自动提取故障深层特征。最后将深层特征连接到Softmax分类器输出故障诊断结果。结果表明,所提出算法平均故障诊断准确度达到了98.09%。此外,向训练集数据样本添加不同强度的高斯白噪声,对SSAE进行训练,提高了其特征表达的鲁棒性。

由于深度学习模型参数调整复杂,选取不当可使模型陷入局部最小或过拟合,影响分类结果。因此,下一步需对参数调整方法进行深入研究。同时考虑获取真实MFLI电路中的数据来验证模型的普适性，以及拓展深度学习理论在电力系统故障诊断领域中的应用。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 张正发,李可军,王卓迪,等.兼具开路故障诊断能力的MMC电容电压测量方法[J].电力系统自动化,2017,41(7):114-119.DOI:10.7500/AEPS20160712008.

ZHANG Zhengfa, LI Kejun, WANG Zhuodi, et al. Measuring method of MMC capacitor voltage with diagnostic ability of open-circuit fault[J]. Automation of Electric Power Systems, 2017, 41(7): 114-119. DOI: 10.7500/AEPS20160712008.

[2] 郭敬梅,曾德辉,王钢,等.基于辅助电路的MMC-HVDC直流故障处理策略[J].电力系统自动化,2016,40(16):90-97.DOI:10.7500/AEPS20151029001.

GUO Jingmei, ZENG Dehui, WANG Gang, et al. Auxiliary equipment based processing strategy for MMC-HVDC DC faults[J]. Automation of Electric Power Systems, 2016, 40(16): 90-97. DOI: 10.7500/AEPS20151029001.

[3] PEREZ M A, BERNET S, RODRIGUEZ J, et al. Circuit topologies, modeling, control schemes, and applications of modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 4-17.

[4] 胡鹏飞,林志勇,周月宾,等.适用于大规模MMC的分布式控制系统及两级均压策略[J].电力系统自动化,2014,38(11):79-84.DOI:10.7500/AEPS20131022006.

HU Pengfei, LIN Zhiyong, ZHOU Yuebin, et al. Distributed control system and two-layer voltage balancing method for large-scale modular multilevel converters[J]. Automation of Electric Power Systems, 2014, 38(11): 79-84. DOI: 10.7500/AEPS20131022006.

[5] 张建坡,赵成勇,郭丽.模块化多电平换流器子模块拓扑仿真分析[J].电力系统自动化,2015,39(2):106-111.DOI:10.7500/AEPS20130821005.

ZHANG Jianpo, ZHAO Chengyong, GUO Li. Simulation analysis on submodule topology of modular multilevel converter[J]. Automation of Electric Power Systems, 2015, 39(2): 106-111. DOI: 10.7500/AEPS20130821005.

[6] YANG Q, QIN J, SAEEDIFARD M. Analysis, detection, and location of open-switch submodule failures in a modular multilevel converter[J]. IEEE Transactions on Power Delivery, 2016, 31(1): 155-164.

[7] DENG F, CHEN Z, KHAN M R, et al. Fault detection and localization method for modular multilevel converters[J]. IEEE Transactions on Power Electronics, 2014, 30(5): 2721-2732.

[8] 李探,赵成勇,李路遥,等.MMC-HVDC子模块故障诊断与就地保护策略[J].中国电机工程学报,2014,34(10):1641-1649.

LI Tan, ZHAO Chengyong, LI Luyao, et al. Sub-module fault diagnosis and the local protection scheme for MMC-HVDC system[J]. Proceedings of the CSEE, 2014, 34(10): 1641-1649.

[9] PEUGET R, COURTINE S, ROGNON J P. Fault detection and isolation on a PWM inverter by knowledge-based model[J]. IEEE Transactions on Industry Applications, 1997, 34(6): 1318-1326.

[10] CHOWDHURY F N, ARAVENA J L. A modular methodology for fast fault detection and classification in power systems[J]. IEEE Transactions on Control Systems Technology, 1998, 6(5): 623-634.

[11] TURPIN C, BAUDESSON P, RICHARDEAU F, et al. Fault management of multicell converters[J]. IEEE Transactions on Industrial Electronics, 2002, 49(5): 988-997.

[12] 龙伯华,谭阳红,许慧,等.基于量子神经网络的电力电子电路故障诊断[J].电工技术学报,2009,24(10):170-175.

LONG Bohua, TAN Yanghong, XU Hui, et al. Fault diagnosis of power electronic circuits based on quantum neural network[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 170-175.

[13] WANG T, XU H, HAN J, et al. Cascaded H-bridge multilevel inverter system fault diagnosis using a PCA and multi-class relevance vector machine approach[J]. IEEE Transactions on Power Electronics, 2015, 30(12): 7006-7018.

[14] 李宁,李颖晖,朱喜华,等.基于混合逻辑动态模型和故障事件识别向量的新型逆变电路故障诊断[J].电网技术,2013,37(10):2808-2813.

LI Ning, LI Yinghui, ZHU Xihua, et al. Fault diagnosis for new inverter circuits based on mixed logic dynamic model and incident identification vector[J]. Power System Technology, 2013, 37(10): 2808-2813.

[15] 陈如清,李强.一种基于频谱分析的可控整流电路故障诊断方法[J].电机与控制学报,2005,9(1):80-85.

CHEN Ruqing, LI Qiang. A method for fault diagnosis in controlled rectifier based on frequency analysis[J]. Electric Machines and Control, 2005, 9(1): 80-85.

[16] 崔江,王强,龚春英.结合小波与Concordia变换的逆变器功率管故障诊断技术研究[J].中国电机工程学报,2015,35(12):3110-3116.

CUI Jiang, WANG Qiang, GONG Chunying. Inverter power switch fault diagnosis technique research based on wavelet and Concordia transform[J]. Proceedings of the CSEE, 2015, 35(12): 3110-3116.

[17] 郑连清,邹涛,娄洪立.电力电子主电路故障诊断方法研究[J].高电压技术,2006,32(3):84-86.

ZHENG Lianqing, ZOU Tao, LOU Hongli. Fault diagnosis of power electronic circuits based on wavelet transform and neural network[J]. High Voltage Engineering, 2006, 32(3): 84-86.

[18] 胡清,王荣杰,詹宜巨.基于支持向量机的电力电子电路故障诊断技术[J].中国电机工程学报,2008,28(12):107-111.

HU Qing, WANG Rongjie, ZHAN Yiju. Fault diagnosis technology based on SVM in power electronics circuit[J]. Proceedings of the CSEE, 2008, 28(12): 107-111.

[19] DAHL G E, YU D, DENG L, et al. Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition[J]. IEEE Transactions on Audio Speech & Language Processing, 2012, 20(1): 30-42.

[20] HANNUN A, CASE C, CASPER J, et al. Deep speech: scaling up end-to-end speech recognition[EB/OL]. [2014-12-19]. https://arxiv.org/obs/1412.5567.

[21] CHEN K, HU J, HE J. A framework for automatically extracting overvoltage features based on sparse autoencoder[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 594-604.

[22] 徐政,屠卿瑞,管敏渊.柔性直流输电系统[M].北京:机械工业出版社,2013.

[23] 李可军,张正发,刘智杰,等.MMC桥臂不对称运行特性分析及子模块故障下的控制策略[J].高电压技术,2016,42(10):3059-3067.

LI Kejun, ZHANG Zhengfa, LIU Zhijie, et al. Characteristics analysis of MMC in arm asymmetrical operation and control strategy under submodule fault[J]. High Voltage Engineering, 2016, 42(10): 3059-3067.

[24] 管敏渊,徐政.模块化多电平换流器子模块故障特性和冗余保护[J].电力系统自动化,2011,35(16):94-98.

GUAN Minyuan, XU Zheng. Redundancy protection for sub-module faults in modular multilevel converter[J]. Automation of Electric Power Systems, 2011, 35(16): 94-98.

[25] TAO C, PAN H, LI Y, et al. Unsupervised spectral-spatial feature learning with stacked sparse autoencoder for hyperspectral imagery classification[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(12): 2438-2442.

[26] XU J, XIANG L, LIU Q, et al. Stacked sparse autoencoder (SSAE) for nuclei detection on breast cancer histopathology images[J]. IEEE Transactions on Medical Imaging, 2016, 35(1): 119-130.

[27] 代杰杰,宋辉,杨祎,等.基于栈式降噪自编码器的输变电设备状态数据清洗方法[J].电力系统自动化,2017,41(12):224-230.DOI:10.7500/AEPS20161201003.

DAI Jiejie, SONG Hui, YANG Yi, et al. Cleaning method for status data of power transmission and transformation equipment based on stacked denoising autoencoders[J]. Automation of Electric Power Systems, 2017, 41(12): 224-230. DOI: 10.7500/AEPS20161201003.

[28] 戴晓爱,郭守恒,任淯,等.基于堆栈式稀疏自编码器的高光谱影像分类[J].电子科技大学学报,2016,45(3):382-386.

DAI Xiaoai, GUO Shouheng, REN Yu, et al. Hyperspectral remote sensing image classification using the stacked sparse autoencoder[J]. Journal of University of Electronic Science and Technology of China, 2016, 45(3): 382-386.

[29] GLOROT X, BORDES A, BENGIO Y. Deep sparse rectifier neural networks[C]// International Conference on Artificial Intelligence and Statistics, April 11-13, 2011, Fort Lorderdale, USA.

[30] ZHU C, BYRD R H, LU P, et al. Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization[J]. ACM Transactions on Mathematical Software, 1997, 23(4): 550-560.

[31] SHAO S, WATSON A J, CLARE J C, et al. Robustness analysis and experimental validation of a fault detection and isolation method for the modular multilevel converter[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3794-3805.