抑制三相四桥臂逆变器共模电压的三维SVPWM控制策略

胡慧慧, 马文忠, 董 磊

(中国石油大学(华东)信息与控制工程学院, 山东省青岛市 266580)

0 引言

在大功率变流系统中,普遍采用脉宽调制(PWM)控制技术的逆变器会产生较大的共模电压,不仅会对电机等负载造成伤害,还会引发共模干扰,影响供电电网电能质量及电网上其他电子设备的正常运行[1-3]。

除了采取加装滤波器[4-5]等被动抑制措施以外,近几年,从逆变器的拓扑结构[6-8]及其控制策略入手进行主动抑制的相关研究方兴未艾。文献[9]提出的三相四桥臂逆变器,通过增加一相桥臂的方式实现了对称工作状态,广泛适用于非线性和不平衡负载供电等领域,相较于传统的三相三桥臂逆变器,抑制共模电压的效果明显。在针对三相四桥臂逆变器控制策略的研究中,文献[10]建立了离散系统的函数模型,并结合预测电流进行控制,降低共模电压的同时减少了输出波形的畸变,但存在模型预测计算量大等问题。文献[11]提出在正弦脉宽调制(SPWM)载波移相的基础上,采用跳变后移的控制策略,确保任何情况下4个桥臂的输出都能达到平衡,但该方法直流电压利用率较低,且输出波形的谐波畸变率较高。目前广泛采用的是三维空间矢量脉宽调制(3D-SVPWM)技术[12-13],因为其具有直流电压利用率高,开关频率较低,数字控制相对简单灵活等优点。

本文借鉴文献[14]的思路,在传统3D-SVPWM控制策略的基础上,进行了优化改进,提出选取参考电压矢量附近两个相反的非零矢量来代替零矢量的方法。仿真结果证明其正确可行,与传统的控制策略相比,在不改变直流电压利用率的情况下,可以有效降低三相四桥臂逆变器输出共模电压的大小。

1 三相四桥臂逆变器及其控制策略

如附录A图A1所示,针对三相四桥臂逆变器的拓扑结构,列写4个回路的KVL方程[15]:

(1)

式中:Vao,Vbo,Vco和Vfo分别为逆变器4个桥臂的输出电压;L为滤波电感;ia,ib,ic和if分别为4个桥臂上流经滤波电感的电流;ZA,ZB和ZC分别为电机每一相的等效阻抗;iA,iB和iC分别为电机每一相的电流;Vno为负载中性点和直流环节两个电容中点之间的电位差。

因为第4个桥臂的存在,给零序电流提供了通路,所以不管三相负载平衡与否,都可以满足ia+ib+ic+if=0,且ZAiA+ZBiB+ZCiC=0,则式(1)中的4式相加可得:

(2)

又因为零点位于直流环节中两个参数一致的电容中间,其与电源地之间的电位差Vog可视为零,所以负载中性点和电源地之间的电位差Vng,也就是共模电压(common-mode voltage,CMV),满足如下关系:

(3)

以开关状态P(仿真时为1)表示上桥臂导通,开关状态N(仿真时为0)表示下桥臂导通,则4个桥臂的开关状态有16种。不同的开关状态对应的共模电压不同,如附录A表A1所示。从表A1可以看出,选择合适的开关状态可以使共模电压为零,即被完全抑制。由于电力电子器件的自身限制及改变开关状态时死区时间的存在,实际中很难完全抑制共模电压,但只要避免选取PPPP和NNNN两个零矢量,就可以把共模电压降低到±Vg/4以内(Vg为直流侧电压),达到有效抑制共模电压的目的。

3D-SVPWM的控制策略源于电机的矢量控制,通过电力电子器件不同开关状态形成的空间矢量,合成逆变器输出的参考电压矢量,从而达到逼近理想电压圆的目的。如图1所示,在α-β-γ坐标系下,16种开关状态构成了一个六棱柱,而六棱柱可分为6个三棱柱[9]。每个三棱柱又分为4个四面体,由此得到24个空间分布的四面体。具体的实现方法为:①判断参考电压矢量位于哪个三棱柱,由图1可以看出,三棱柱的判断与γ轴无关,可将六棱柱投影至α-β平面(如图2所示),转换为确定参考电压矢量在α-β平面上的投影位于哪个扇区;②四面体的判断,确定选取哪三个相邻的非零矢量和两个零矢量来合成参考电压矢量,图2中第4个桥臂的状态需要根据其他三个桥臂的状态确定;③确定上述几个合成矢量在一个控制周期内的作用时序和对应的占空比,选择具体的调制方案,即控制三相四桥臂上电力电子器件的开关时序和作用时间,从而输出可调的PWM电压。

2 改进的3D-SVPWM控制策略

为有效降低共模电压,本文提出选取参考电压矢量附近两个相反的非零矢量来代替零矢量。表1给出了6个三棱柱中24个四面体所对应的两个代替零矢量和三个相邻非零矢量。

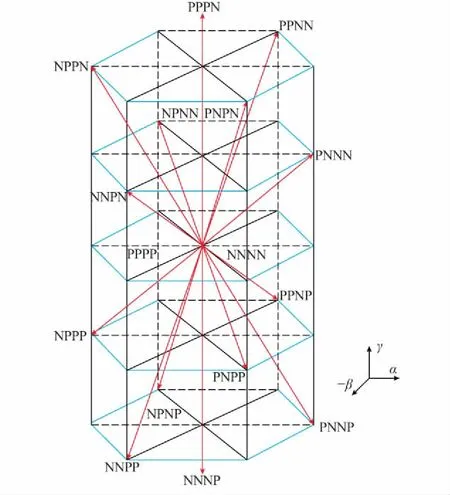
图1 四桥臂开关状态矢量空间分布Fig.1 Space distribution of four-leg switch state vectors

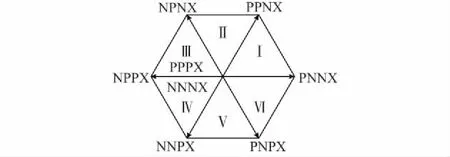
图2 三维空间矢量在α-β平面投影图Fig.2 α-β plane projection of 3D space vector

下面以三棱柱Ⅰ为例进行深入分析,传统3D-SVPWM控制策略选取的三个相邻非零矢量和两个零矢量(PPPP和NNNN)组成的四面体,如图3所示。由表1可知,采用改进控制策略后,四面体a和四面体b均选取PNPN和NPNP代替零矢量,它们在α-β平面上的投影与第Ⅰ扇区的中心线垂直,这也从空间上满足四面体的分布相对平衡。四面体c选取PNNP和NPPN代替零矢量,它们在α-β平面上的投影位于第Ⅰ和第Ⅵ扇区的分界线上。而四面体d选取PPNN和NNPP代替零矢量,它们在α-β平面上的投影位于第Ⅰ和第Ⅱ扇区的分界线上,这是因为三个相邻非零矢量中分别有PPPN和NNNP两个投影在中心的矢量,造成四面体的重心偏移。根据三棱柱和四面体的不同,两个非零矢量的选取具有一定规律性。

表1 代替零矢量的两个非零矢量的选择Table 1 Selection of two non-zero vectors for replacing zero vector

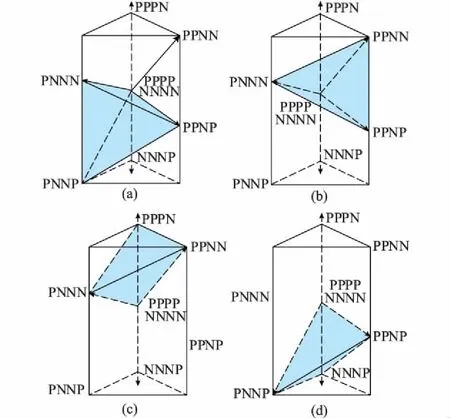
图3 三棱柱Ⅰ中的四面体Fig.3 Tetrahedrons of tri-prism Ⅰ

选定好合成矢量之后,接下来确定各个矢量的作用时序。以Sa,Sb,Sc,Sf分别代表四桥臂开关状态;d1,d2,d3分别代表三个非零矢量在一个开关周期内作用时间的占空比;以d0代表两个零矢量作用时间的占空比。以三棱柱Ⅰ中的四面体a为例,如图4所示,选取PNPN(1010)和NPNP(0101)代替零矢量NNNN(0000)和PPPP(1111),且作用时间相同,则在一个开关周期内输出电压的平均值没有发生变化,这说明改进后的控制策略可保持直流电压利用率不变。

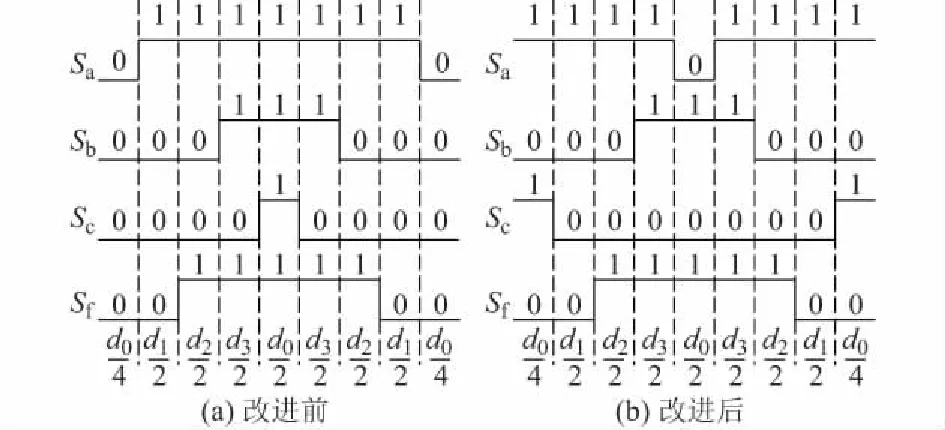
图4 四桥臂开关器件的作用时序和占空比Fig.4 Time sequence and duty ratio of four-leg switching

3 仿真与分析

本文采用MATLAB/Simulink进行建模仿真。系统仿真参数为:直流侧电压400 V;三相滤波电感和中线电感5 mH;三相滤波电容210 μF;三相负载平衡时,每相电阻R=10 Ω,电感L=5 mH;不平衡负载时,A相负载变为R=12 Ω,电感L=7 mH,B相和C相不变;PWM开关频率为5 kHz。

3.1 系统稳定状态下的分析

不论系统带平衡负载还是不平衡负载,3D-SVPWM控制策略改进前后的逆变器三相输出电压和电流几乎没有发生变化(仿真结果如附录A图A2和图A3所示)。系统带平衡负载时,采用传统的3D-SVPWM控制策略输出电压谐波畸变率为1.15%,采用改进的控制策略输出电压谐波畸变率为1.27%;系统带不平衡负载时,采用传统的3D-SVPWM控制策略输出电压谐波畸变率为1.32%,而采用改进的控制策略输出电压谐波畸变率为1.45%。通过分析可知,谐波畸变率的增加是因为传统的3D-SVPWM控制策略每个开关周期以零矢量开始又以零矢量结束(如图4所示),所以输出波形具有对称性,谐波含量相对较少,但是改进的控制策略没有选用零矢量,在开关周期变化时失去了输出电压波形的对称性,也就导致输出电压谐波畸变率略有增加,但仍旧满足国标GB/T 14549-93《电能质量公用电网谐波》所规定的小于5%的要求。

从附录A图A2和图A3中还可以看出,在传统的3D-SVPWM控制策略下,共模电压约在±Vg/2(±200 V)左右,而采用改进的3D-SVPWM控制策略后降低到±Vg/4(±100 V)左右,达到了有效降低共模电压的目的。

3.2 系统状态变化时的分析

附录A图A4(a)为采用改进的3D-SVPWM控制策略,系统由平衡状态转为不平衡状态时输出电压、输出电流及共模电压的变化。显然在0.1 s时,因为负载的不平衡,导致输出电流发生了明显变化,但是输出电压几乎没有改变,同时共模电压也只是略微有些波动,变化并不明显。

如附录A图A4(b)所示为系统突加、突减负载时输出电压、输出电流及共模电压的变化。可以看出,在0.2 s时,负载突然增加,造成了输出电流的增大,在0.4 s时,负载突然减小,输出电流也相应变小。然而整个过程中,输出电压和共模电压几乎没有发生变化,保持恒定。这些都反映出改进后的3D-SVPWM控制策略对动态变化过程同样具有良好的控制效果。

4 结语

本文针对三相四桥臂逆变器提出了一种改进的3D-SVPWM控制策略。在进行参考电压矢量合成的过程中,采用参考电压矢量附近相反的两个非零矢量来代替零矢量的方法。具体的选取原则如下。

1)两个非零矢量单独作用时,产生的共模电压为零。

2)两个非零矢量大小相等,方向相反。

3)两个非零矢量与另外三个相邻的非零矢量之间满足开关状态变化最小,即有最少的开关器件动作。

该方法在不影响合成效果的情况下,避免了零矢量的作用。仿真结果表明,改进后的控制策略不受负载平衡状态和动态扰动等方面的影响,在不改变直流电压利用率的前提下,可有效降低逆变器的共模电压,从而达到主动抑制的目的。

此外,本文所提方法在抑制共模电压的同时,仍然造成了谐波畸变率的小幅增加,如何能够有效解决这一问题将是下一步的研究方向。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 张怡海.PWM逆变器驱动异步电机系统的共模电压研究[D].四川:西南交通大学,2014.

[2] 姜艳姝,于晓洋,艾跃,等.PWM多驱动系统中的共模电压及其抑制[J].电机与控制学报,2010,14(11):44-48.

JIANG Yanshu, YU Xiaoyang, AI Yue, et al. Common-mode voltage and its cancellation in PWM multi-drive system[J]. Electric Machines and Control, 2010, 14(11): 44-48.

[3] HU Anping, XU Dewei, WU Bin, et al. Reference trajectory optimized SVM for high power current source converters to improve harmonic performance and reduce common mode voltage[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3488-3498.

[4] HABETLER T G, NAIK R, NONDAHL T A. Design and implementation of an inverter output LC filter used for dv/dtreduction[J]. IEEE Transactions on Power Electronics, 2002, 17(3): 327-331.

[5] OGASAWARA S, AYANO H, AKAGI H. An active circuit for cancellation of common mode voltage generated by a PWM inverter[J]. IEEE Transactions on Power Electronics, 1998, 13(5): 835-841.

[6] 王志华,尹项根,程汉湘,等.级联型高压变频调速系统共模电压分析[J].电力系统自动化,2003,27(15):58-62.

WANG Zhihua, YIN Xianggen, CHENG Hanxiang, et al. Common mode voltage analysis of cascaded MV-VFD[J]. Automation of Electric Power Systems, 2003, 27(15): 58-62.

[7] 王浩,何晋伟,贾宏杰.面向微网群的多端口电流源变流器共模电压抑制仿真[J].电力系统自动化,2017,41(18):74-79.DOI:10.7500/AEPS20170224006

WANG Hao, HE Jinwei, JIA Hongjie. Common-mode voltage suppression simulation for multi-port current source converter of microgrid clusters[J]. Automation of Electric Power Systems, 2017, 41(18): 74-79. DOI: 10.7500/AEPS20170224006.

[8] 王跃,赵文健,胡耀威,等.T型H桥级联多电平变换器的改进型脉宽调制策略[J].电力系统自动化,2016,40(19):87-93.DOI:10.7500/AEPS20150404002.

WANG Yue, ZHAO Wenjian, HU Yaowei, et al. Improved phase width modulation strategy for T-type H-bridge based cascaded multilevel converter[J]. Automation of Electric Power Systems, 2016, 40(19): 87-93. DOI: 10.7500/AEPS20150404002

[9] ZHANG R, PRASAD V H, BOROYEVICH D, et al. A three-phase inverter with a neutral leg with space vector modulation[C]// Conference Record of IEEE on APEC, February 27, 1997, Atlanta, GA, USA: 851-863.

[10] GARCIA C, RIVERA M, LOPEZ M, et al. Predictive current control of a four-leg indirect matrix converter with imposed source currents and common-mode voltage reduction[C]// Energy Conversion Congress and Exposition (ECCE), September 15-19, 2013, Denver, CO, USA: 982-989.

[11] 黄劲,熊蕊,王志,等.采用三相四桥臂抑制逆变器共模干扰的SPWM控制策略[J].电工技术学报,2003,24(3):110-115.

HUANG Jin, XIONG Rui, WANG Zhi, et al. SPWM control strategy to reduce inverter common-mode interferences based on three-phase four-leg structure[J]. Transactions of China Electrotechical Society, 2003, 24(3): 110-115.

[12] ORTJOHANN E, MOHD A, HAMSIC N, et al. Design and experimental investigation of space vector modulation for three-leg four-wire voltage source inverters[C]// 13th European Conference on Power Electronics and Applications, September 8-10, 2009, Barcelona, Spain: 1-6.

[13] PERALES M A, PRATS M, PORTILLO R, et al. Three-dimensional space vector modulation in abc coordinates for four-leg voltage source converters[J]. IEEE Power Electronics Letters, 2003, 1(4): 104-109.

[14] ZHANG M, ATKINSON D, JI B, et al. A near-state three-dimensional space vector modulation for a three-phase four-leg voltage source inverter[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 5715-5726

[15] 黄劲.基于三相四桥臂逆变器的机驱动系统EMC及可靠性研究[D].武汉:华中科技大学,2009.