基于历史行驶路线的电动汽车充电站布局优化
2018-06-21付凤杰方雅秀董红召陈炜烽
付凤杰, 方雅秀, 董红召, 陈炜烽
(1. 浙江工业大学机械工程学院, 浙江省杭州市 310014; 2. 杭州数元信息科技有限公司, 浙江省杭州市 310012)
0 引言
目前,已经有包括美国、荷兰、挪威、印度、法国和英国等在内的多个国家公布禁售燃油汽车时间表或禁售燃油汽车初步计划。中国工信部于2016年曾发布《乘用车企业平均燃料消耗量与新能源汽车积分并行管理办法(征求意见稿)》,并于2017年启动了燃油汽车退出时间表的研究。这意味着燃油汽车与电动汽车将进入快速此消彼长过程,而充电设施的合理规划和建设是电动汽车电量需求的保障,是进一步促进电动汽车推广和发展的关键。
现有的充电站布局优化模型按照充电需求的计算方法主要分为两类。第一类模型利用交通流量等参数直接计算充电需求[1-4],该类模型侧重于充电站布局方案的优化求解方法,弱化充电需求的计算过程,最终优化方案不符合实际充电需求。第二类模型通过模拟电动汽车出行,对充电需求进行计算,使得优化方案更加合理。例如部分研究根据交通出行分布的特征,包括平均出行距离、平均出行次数以及出行时间概率分布等,利用蒙特卡洛方法模拟电动汽车的出行时间以及出行路线[5-7];部分研究认为,典型交通出行链影响电动汽车的充电行为,并对电动汽车的出行链进行了模拟[8-10]。但是上述出行模拟过程仅考虑所有车辆的出行分布规律,忽略了不同车辆之间的个体差异性,导致电动汽车出行及充电行为的模拟结果与实际相比仍存在较大偏差,相应的充电站布局方案仍然难以满足实际充电需求。因此,越来越多的学者利用车辆的轨迹数据来模拟出行,提高充电需求的计算精度。例如文献[11]在优化电动出租车充电站布局时,利用全球定位系统(GPS)轨迹数据获取出租车停留次数,将日均停留次数作为充电需求[11]。但是出租车GPS数据覆盖率过小,并且出租车出行不能代表所有小汽车或电动汽车的出行。与出租车GPS数据相比,高清卡口能够获取所有通过车辆的信息,许多研究对基于高清卡口的自动车辆识别(ANPR)数据进行处理,获取过往车辆的节点信息和行驶路线等[12-14]。基于ANPR数据的车辆历史行驶路线能够为电动汽车充电需求的计算提供更加合理、精确的模拟基础。
另外,从优化目标出发,充电站优化布局模型可以分为三类。第一类是电动汽车用户最优模型,如电动汽车充电成本最小模型[7,9]、充电次数最少模型[11]和服务最优模型[15];第二类是充电站运营商最优模型,如投资成本最小模型[16-17]和充电车辆数最大模型[18]。这两类模型仅仅考虑了电动汽车用户利益或运营商利益,相应的充电站布局方案实施之后,可能出现运营商亏损,继而无力经营或电动汽车用户充电成本过高,继而放弃电动汽车出行的结果。因此,第三类模型综合考虑电动汽车充电成本和运营商建设成本[19],使得充电站布局方案能够同时满足电动汽车用户和运营商的需求。
综上所述,本文利用基于ANPR数据的车辆历史行驶路线模拟电动汽车的实际出行;在给定一种充电站布局方案后,根据电动汽车的行驶路线、电池类型和剩余里程等信息计算其充电需求;并综合考虑电动汽车的充电成本、运营商的利润和电网负荷,利用遗传算法对充电站选址及定容进行优化;最终确定充电站的最优布局方案。
1 电动汽车出行需求
受出行特点影响,不同类别车辆的充电需求不同,本文将电动汽车分为电动私家车、电动出租车和电动公共汽车三类。由于电动公共汽车有固定的出行路线和发车时刻表,并且往往建设有专用充电站,本文研究对象仅包括电动私家车和电动出租车。若已知一日内电动私家车的出行量、电动出租车的出行量和每辆电动汽车的行驶路线,即可模拟电动汽车的出行,为计算其充电需求提供基础。
1.1 电动汽车出行量
假设城市内电动私家车的保有量和私家车的保有量之比,与电动私家车的出行量和私家车的出行量之比相等,将该比值称为电动私家车占比,即
(1)
式中:QEPV和QPV分别为电动私家车和私家车的保有量;NEPV和NPV分别为电动私家车和私家车的出行量;ηEPV为电动私家车占比。
利用高清卡口数据,将研究区域中一日内出现的私家车车牌总数(重复出现记为1个)作为私家车的出行量NEPV,QPV和QEPV可以从交通部门等获取。因此,可以利用式(1)计算得到NEPV。
同理,利用式(2)计算电动出租车的出行量为:
(2)
式中:ηETX为电动出租车占比:QETX和QTX分别为电动出租车和出租车的保有量;NETX和NTX分别为电动出租车和出租车的出行量。
随着新能源汽车专用牌照的逐步推广和普及,可以根据新能源汽车专用牌照的特点,如车牌颜色和车牌号码,利用高清卡口采集数据直接计算得到各种新能源汽车的出行量。
1.2 车辆历史行驶路线获取
当用户同时拥有燃油汽车和电动汽车时,可能出现用户因电动汽车电量不足选择燃油汽车出行的情况,导致电动私家车的实际出行量有所降低。同时拥有燃油汽车和电动汽车的用户比r2以及用户的选择率rc决定了电动私家车的出行选择系数rsc,即rsc=1-r2rc。因此,本文随机选取NEPVrsc个私家车行驶路线和NETX个出租车行驶路线,用于模拟电动私家车的出行。
为减小计算时间、简化优化过程,本文做出如下两个假设:①充电站、家、公司和商场等建筑均布设在交叉口位置,因此,后文中车辆的行驶路线或充电站的布局方案均用节点集合来表示;②城市路网内,车辆多为短途出行,电动汽车出行受充电时间和续航里程的限制较小,因此在新能源汽车专用牌照普及之前,本文假设电动汽车的出行特点与非电动汽车的出行特点相似。
私家车工作日主要进行通勤出行,因此始发节点、目的节点和停留节点的判别为模拟其充电选择行为提供依据;而出租车一日出行由多次载客出行、多次空载出行和交班构成,应根据日出行距离和行驶路线模拟其充电选择行为,重要节点不存在实际意义,不进行判别。
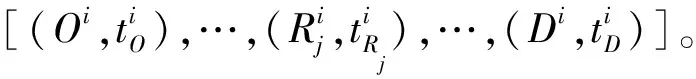
1.2.1高清卡口采集的单车数据
利用高清卡口数据可以获取车辆的车牌号、交叉口编号、进口道方向、进口车道、通过时刻和车辆类型(处理得到)。虽然高清卡口系统日益普及,但是仍有部分交叉口未安装检测设备,会出现车辆采集信息缺失的情况,导致连续两个通过节点并不相邻。以车牌号为“浙AF004Q”的私家车(作者所有,不涉及隐私)为例,一日内高清卡口采集数据如表1所示。因此需要进一步确定其行驶路线。
1.2.2确定行驶路线
高清卡口数据编号规则为:进口方向编号1,2,3和4依次代表东西南北进口,车道编号由内向外(道路黄线到路缘石)依次为1,2,3,…,具体见附录A图A1。由进口方向和车道编号可以确定车辆在当前节点的转向行为,根据车辆的转向行为和最短路径连接非连续通过节点,最终确定车辆行驶路线[20],具体见附录A图A2。
1.2.3确定重要节点
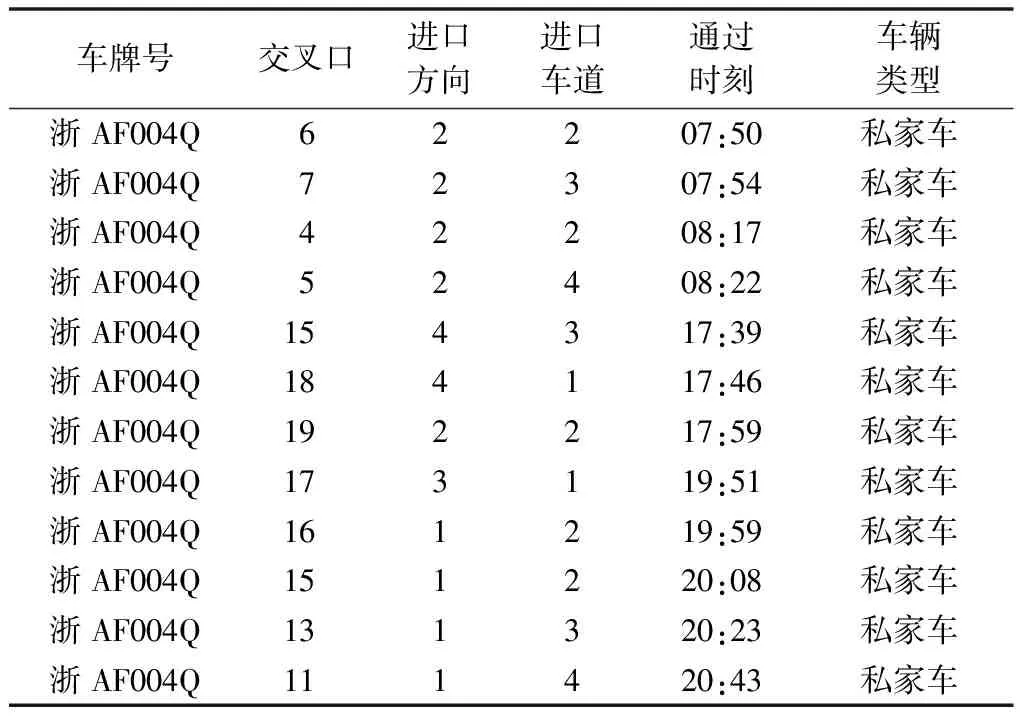
表1 一日内高清卡口采集的单车数据Table 1 Observed data of an individual vehicle in one day from high-definition gate
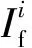
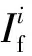
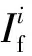
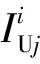
(3)
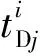
根据路网拓扑结构确定车辆“浙AF004Q”的始发节点和目的节点均为节点6;根据表1所示数据,可以得知车辆在节点5和15通过时刻之差高达557 min,在节点19和17的通过时差为112 min,继而确定节点5和19为两个停留节点。
1.3 电动汽车出行模拟
目前市场上电动汽车的电池类型繁杂,根据续航里程将现有电动私家车电池归为5类,其续航里程分别为150,200,250,300,400 km,5种车型数量比为1∶3∶3∶2∶1;将电动出租车电池归为2类,续航里程分别为200 km和300 km,数量比为6∶4。电动私家车中个人常规充电桩拥有情况为:拥有家用常规充电桩、拥有单位专用常规充电桩和无常规充电桩的电动汽车数量比例为1∶1∶8。将电池类型和个人常规充电桩拥有情况按照上述比例随机分配给电动汽车。
用剩余里程比rr(剩余里程Lr与续航里程Le之比)表示电池的使用状态,一日出行开始时刻电动私家车电池的初始状态各不相同,并非全是满电,即初始剩余里程比各不相等。考虑电池寿命和用户充电习惯,假设初始剩余里程比rr0最小值取为0.1,最大值取为1,并在[0.1,1]之间随机均匀分布。因此,初始剩余里程比的设置可以模拟任意出行日内的任意车辆的初始状态。最终得到每辆电动汽车的出行信息,如表2所示。
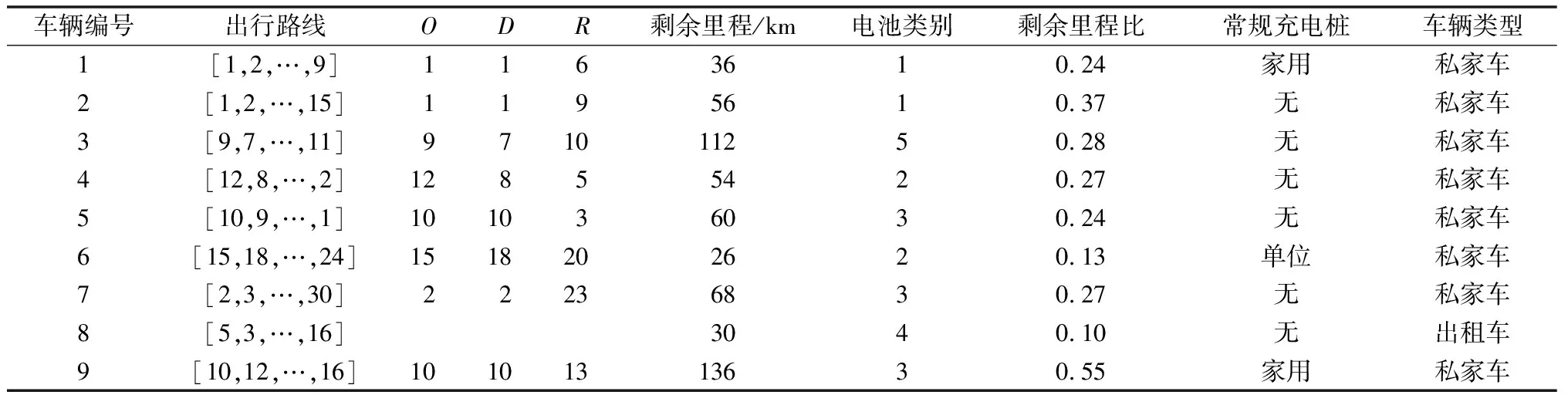
表2 电动汽车出行信息Table 2 Travel information of electric vehicles
2 电动汽车充电需求
电动汽车的充电模式有常规充电和快速充电两种,常规充电时间较长,电池荷电状态从0%~100%往往需要5~8 h;快速充电时间短,电池荷电状态从0%~80%一般需要20~40 min。因此,大部分私家车选择在公司停车场或结束一日出行后在住宅区附近(即出行的停留节点或目的节点)进行常规充电,少部分私家车因应急会选择在出行过程中进行快速充电,大部分出租车由于一日出行距离较长,快速充电成为其电量的主要来源。
2.1 充电行为
2.1.1充电价格
区域电网负荷随时间变化,白天用电负荷较大,春秋季节用电负荷较小(见附录A图A3)。为减小白天电网负荷,应通过定价来诱导电动汽车的充电选择行为:不同功率充电模式、不同充电时段以及不同充电时长下,充电价格应有所不同,充电价格由电费和服务费两部分组成。根据燃油汽车每千米油耗和汽油价格,制定电动汽车的充电价格,具体参照附录A表A1。
2.1.2充电模式选择
利用出行路线中停留时间最大的停留节点将私家车一日出行分为去程和回程。一日出行开始时刻,充电价格、电动私家车的剩余里程数和出行结束时刻决定其充电选择行为,具体情况见图1。图中:LOD为一日往返出行总距离。对于拥有家用常规充电桩的电动私家车,若剩余里程数小于单向出行距离LO,车辆在去程中进行快速充电;若剩余里程大于单向出行距离但是小于往返总距离LOD,车辆在回程中进行快速充电;若剩余里程满足当日出行却不能满足第二日出行,即大于往返出行总距离,却小于双倍往返出行总距离,车辆在出行结束时刻进行常规充电;若剩余里程大于双倍往返出行总距离,车辆当日不进行充电。对于有单位专用常规充电桩和无个人充电桩的电动私家车,充电选择行为略有不同。其中,在剩余里程大于单向出行距离但是小于往返总距离时,前者选择在单位进行常规充电;在剩余里程大于往返出行总距离,却小于双倍往返出行总距离时,前者不进行充电,后者则需要根据实际情况选择在充电站进行常规充电或快速充电。
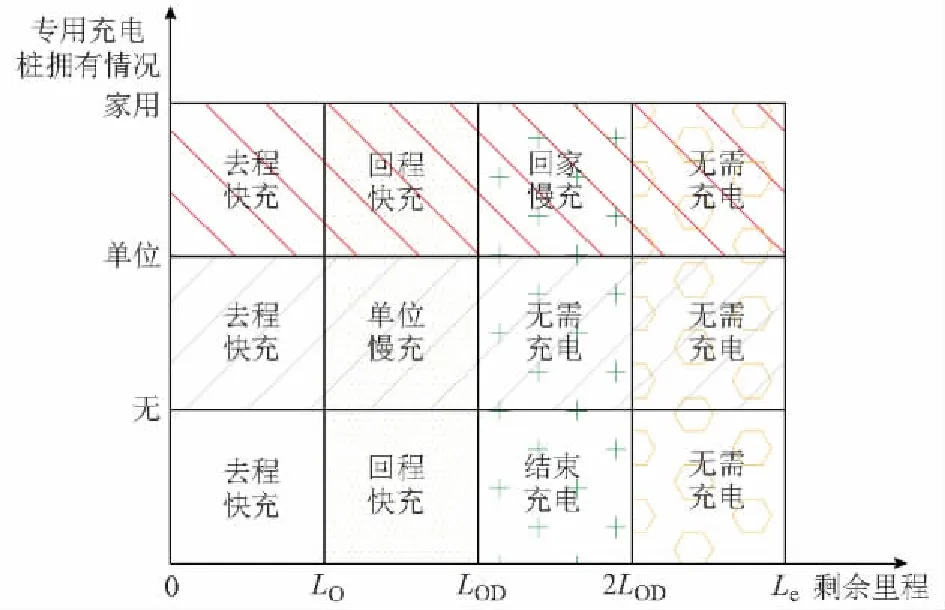
图1 电动私家车剩余里程与充电模式选择Fig.1 Remainder range and charging pattern of private electric vehicle
2.1.3充电时间
车辆出行过程中进行快速充电时,为减小出行行程时间和充电费用,快速充电电量和时间仅需满足当日出行需求,即
(4)
式中:Ef和Tf分别为快速充电电量和时间;Pf为快速充电功率,一般可选30,60,90 kW;e为单位里程耗电量,具体取决于车辆的电池性能;·表示向上取整。
无个人充电桩的电动汽车在出行结束后若选择快速充电,此时车辆往往不考虑出行行程时间,可使得电池电量达到80%(因为达到80%以后必须转为常规充电),此时快速充电电量Ef和时间Tf计算方法如下:
(5)
式中:C为电池容量。
常规充电电量和时间应满足电动私家车由剩余里程到达续航里程,计算方法如下:
(6)
式中:En和Tn分别为常规充电电量和时间;Pn为常规充电功率,一般取值为7 kW。
综上,5种类型电池的快速充电功率和单位里程耗电量指标如附录A表A2所示。
为方便乘客出行,电动出租车一般在空车出行时选择最近充电站进行快速充电。假设剩余里程比rr=0.2时,出租车开始寻找最近充电站,根据其出行路线可以模拟并计算一日内的快速充电需求。每次充电时间的计算方法同样可以用式(5)表示。
2.2 充电成本
电动汽车充电成本的计算不仅要包括空驶成本[9],还应考虑充排队等待和充电费用,即
cuser=cl+cw+cec
(7)
式中:cuser,cl,cw,cec分别为充电总成本、空驶成本、充电站内等待充电的排队损失成本和充电费用。
2.2.1空驶成本
参照文献[9],私家车空驶成本计算方法如下:
cl=cOS+cSD-cOD
(8)
式中:cOS为车辆从始发节点至充电站的出行成本;cSD为车辆从充电站到目的节点的出行成本;cOD为始发节点与目的节点间最短路径的出行成本。出租车由于在空车出行时进行充电,其空驶成本为当前所处节点到最近充电站的出行成本cCS,即c1=cCS。
一般用行驶时间表示出行成本,影响因素为行驶路线上各个路段的长度和路段平均行驶速度,因此出行成本计算方法为:
(9)
式中:Tttm为路段m的平均行程时间;Lm为行驶路线上路段m的长度;vm为路段m的平均速度;M为路段个数。
考虑与充电费用单位一致,本文采用出行过程中的用电损失代表出行成本,计算方法如下:
(10)
式中:vlim,m为路段m的限速;ψh为峰电充电价格;κ为时间价值,当时间小于30 min时,本文取值为25元/h,当时间大于30 min时,取值为40元/h。
2.2.2排队等待损失成本
充电车辆在抵达快速充电站时,若没有空闲充电桩,则需进行排队等待。若等待充电的车辆过多,且剩余里程能够保证车辆达到下一充电站,则车辆更换充电站,否则在该充电站等候充电。某一车辆j的排队等待损失成本的计算步骤如下。
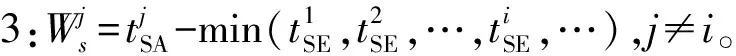
由于常规充电时间较长,当充电车辆抵达常规充电站时,若没有空闲充电桩,车辆直接更换充电站,所以等待损失成本为0,空驶成本增大。
2.2.3充电费用
充电费用取决于充电电量E和充电价格ψ,利用式(11)计算充电费用cec。
cec=Eψ
(11)
式中:ψ为充电价格,不同充电模式和充电时刻,ψ的取值不同,具体参照附录A表A1。
3 优化模型
常规充电需求的计算能够细化快速充电需求,但是由于常规充电桩往往布设在公共停车场,且对配电网影响较小。因此,本文仅给出常规充电桩的最小密度计算方法,充电站的布局优化则针对快速充电站。
根据电动汽车的出行需求和充电需求,可以对充电站进行布局优化,包括优化充电站的数量、充电站选址及定容。本文综合考虑用户充电成本、运营商利润和电网负荷,建立布局优化模型。
3.1 充电桩最小密度计算
充电桩最小密度指标能够为运营商提供基本依据。将整个规划对象看作一个完整区域,并根据交通小区或行政区等标准将其划分为若干子区。根据区域(或各个子区)内的充电需求和面积a计算相应的充电桩最小布设密度。考虑以下两种情况。
1)每个电动汽车都拥有个人常规充电桩(Zp=Nn),则无须考虑常规充电站布设。其中,Nn为需进行常规充电的车辆数,Zp为个人常规充电桩数。
2)部分电动汽车无个人常规充电桩(Zp 3.1.1常规充电桩的最小密度 无常规充电桩的车辆在出行结束后选择居住地附近的常规充电站进行充电,利用电动私家车常规充电开始时刻、充电时间和充电车辆数可以计算得到最小密度,具体步骤如下。 步骤2:令i=i+1,i∈V,j=0。其中,V为车辆i目的节点一定半径内的常规充电车辆的集合,集合V随着上述步骤不断更新。 步骤3:令j=j+1,j≠i,j∈V。 3.1.2快速充电桩的最小密度 (12) (13) 当充电站选址不合理导致电动车辆在剩余里程内无法到达最近充电站,或者充电站规模设置不当,导致电动车辆选择其他充电站时,充电站的运营收入降低。因此影响充电站利润的影响因素有充电站的选址及成本、充电站的数量、充电桩的数量、充电价格。 3.2.1充电站的选址及成本 受地价以及周边用地性质等因素影响,不同地理位置下充电站的建设成本不同。假设充电站s的面积为as,单位面积的地价为φ1,建筑成本为φ2,单个充电桩成本为φ3,年维护运营成本为φ4,其他成本为φ5,则以Y年为限,利用式(14)计算充电站s的成本cs。 (14) 3.2.2运营收入 充电站的收入来源于电动车辆的充电费用,即总充电电量与充电价格之积,充电站s在Y年内的收入为: (15) 式中:φi为电动汽车i充电时充电站的放电成本,放电成本取决于充电站用电容量和放电时刻,峰电和谷电放电成本不同。 充电站的优化布局过程中,需考虑以下约束条件:充电站选址受限、电动车辆剩余电量下限、最近充电站位置、空驶距离最大接受值、最小密度和电网负荷等。 3.3.1充电站选址受限 3.3.2电动车辆剩余电量下限 为保护电动车辆电池寿命,设定车辆能够进行充电时剩余里程比rr≥0.05;车辆初始剩余里程比设为rr0≥0.1。 3.3.3最近充电站位置 车辆i进行快速充电时与最近充电站的距离应小于剩余里程。 3.3.4空驶成本最大忍受值 车辆i进行快速充电的空驶成本应小于其最大忍受值cl,max。 3.3.5最小充电桩个数 充电桩的数量应大于最小充电桩数。 3.3.6用电容量 充电站用电负荷受限于其用电容量,用电容量的设置受限于当前区域配变规模及规划新增规模,而区域内总用电容量小于该区域配变容量。根据配电网现状,将规划区域划分B个子区,每个子区内充电站和充电桩的数量必须满足: (16) 由于不同用户对相同充电成本的接受程度不同,取决于用户的出行成本,成本—收益比常用于评价投资的回报能力,该比值能够更好地反映充电站的盈亏能力,用户的总充电成本和运营商的总收益可能存在较大差距,本文选择用户充电—出行成本比(CTR)与运营商的成本—收益比(CBR)之和为优化目标,提出优化模型M1。即 (17) (18) 在出行模拟和充电需求计算的基础上,利用遗传算法对优化模型进行求解,确定充电站的最佳选址及最佳容量,求解过程如附录A图A4所示。 某城市某一行政区域含有151个信号交叉口和30个可接入负荷点,路网结构如附录A图A5所示。图中圆圈代表可接入负荷点位,主要是指大型商场、交通枢纽等有足够空间和配变容量能够建设充电站的点位。附录A图A5以子区A为例,展示了信号交叉口点位、可接入负荷点位以及路段长度。 根据交通部门基础数据及高清卡口采集数据,经过处理和计算得到机动车出行量等参数:QPV=126 000,NPV=108 000,QEPV=2 098,NEPV=1 798,QTX=1 651,NTX=1 320,QETX=82,NETX=65。 利用上述方法和数据,得到规划区域内充电站的优化布局方案如图2所示,五角星代表充电站,数字表示充电桩数量。为方便后文对比分析,本文将该优化布局方案称为方案1。 图2 规划区域内充电站的优化布局方案1Fig.2 Optimized allocation scheme 1 of charging station in study area 以子区A为例,对优化方案做进一步分析。图3和图4展示了子区A内CTR总和、CBR总和以及优化目标值随布局方案的变化曲线。图4中任意圆圈代表当前充电站数量下的优化布局方案,包括充电站的选址(红色数字表示)和充电桩数量(黑色数字表示)。 图3 CTR总和与CBR总和的变化曲线Fig.3 Variation curves of sums of CTR and CBR 图4 不同充电站布局方案下优化目标值变化曲线Fig.4 Variation curves of objective under different allocation schemes for charging station 由图3可以看出:①CBR总和随着充电站个数的增加而增大,当充电站个数大于5时,CBR总和骤然增加,因为当充电站过多时,部分充电站收益过低,甚至为0;②CTR总和随着充电站个数的增加整体逐渐减小,但是当充电站数取值为5和6时,CTR总和有所不同,因为充电站个数固定时,最优方案的确定同时会受CBR总和的影响。 由图4可以看出:①当充电站个数为3,充电站选址和定容分别为[3,9,42]和[12,11,3]时,对应的优化目标值最小,因此,将其作为最优布局方案;②当充电站个数大于3时,部分充电站内充电桩的数量为2,这是由于充电站数量过多,部分充电站的充电车辆数过少甚至为0,将其充电桩数量设置为最小值2;③当充电站个数大于5时,优化目标值骤然增加,因为CBR总和显著增大。 利用非工作日下的ANPR数据模拟电动汽车出行,最终得到优化布局方案2。由附录A图A6可以看出,方案2下,子区A内充电站的个数和选址相同,充电桩的数量减少;子区B和C内充电站和相应充电桩数量都减少,其中子区B内,南部充电站与原充电站相邻。这是由于非工作日内,车辆出行的出发时刻较为分散,导致充电行为相对分散,每个充电站内充电桩数量减小。因此,可以选择基于历史工作日内车辆的行驶路线对充电站的布局进行优化设计。 随着电动汽车保有量的增长,充电需求随之增加,假设电动汽车保有量的增长率λEPV取决于两个因子:小汽车保有量的增长率λPV(小汽车保有量增长值/上一年机动车保有量)和电动汽车推广率λin(电动汽车保有量比的增长值/上一年电动汽车保有量比),则有 (19) 由于电动汽车保有量和出行量大幅提升,充电站的数量和容量必定随之增加。方案3中,所有可接入负荷点均需建设充电站,同时充电桩数量大大增加(不考虑配变容量情况下),子区A,B,C内充电桩总数分别高达1 883,1 284,1 124。此时,每个充电站内电动汽车充电时排队等待时间过长,用户CTR总和过大。因此,必须大力发展电池技术,否则充电难、充电服务水平低将一直制约电动汽车的发展。 假设Yin年后,电动汽车电池性能有较大提升,相关参数值发生变化,更新为附录A表A3。 此时,最优充电站布局方案下,充电站数量为可接入负荷点数,充电桩总数减少67%,充电站的规模仍然较大。一方面说明电池技术的发展和续航里程的提升使得一日内充电车辆数减少,继而缓解电动汽车充电难的问题;另一方面也说明,续航里程的提升同时会导致充电时间增大,用户CTR总和仍然过大,必须同时建设电池更换站,才能本质上保证电动汽车的电量需求。 本文利用基于ANPR数据的车辆历史行驶路线模拟电动汽车的出行,计算电动汽车的充电需求,以充电汽车CTR与运营商CBR之和最小为优化目标,最终确定充电站的最优布局方案。 1)基于车辆历史行驶路线的电动汽车出行模拟结果与实际更加吻合,能够提供充电需求的计算精度,提高充电站优化布局方案的合理性,并且案例分析验证了优化方法的有效性。 2)相对于非工作日,工作日的ANPR数据更有代表性,更适用于历史路线的获取和电动汽车出行模拟。 3)随着机动车保有量增长和电动汽车的推广,仅仅通过建立更多更大规模的充电站已经无法满足急剧增加的充电需求,电池技术的发展和突破成为关键。 未来的研究工作将从以下三点入手:①考虑充电站、充电桩智能联网,避免电动汽车出现因排队较长而频繁更换充电站的情况,减小电动汽车的充电等待时间,降低充电成本;②改善模型求解方法,降低路网较大或可接入负荷点数较多时,运行时间过长的问题;③考虑电池更换站与快速充电站同时建设情况下的优化布局问题。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 参考文献 [1] CHEN Z, LIU W, YIN Y. Deployment of stationary and dynamic charging infrastructure for electric vehicles along traffic corridors[J]. Transportation Research Part C: Emerging Technologies, 2017, 77: 185-206. [2] SATHAYE N, KELLEY S. An approach for the optimal planning of electric vehicle infrastructure for highway corridors[J]. Transportation Research Part E, 2013, 59(11): 15-33. [3] 李如琦,苏浩益.基于排队论的电动汽车充电设施优化配置[J].电力系统自动化,2011,35(14):58-61. LI Ruqi, SU Haoyi. Optimal allocation of charging facilities for electric vehicles based on queuing theory[J]. Automation of Electric Power Systems, 2011, 35(14): 58-61. [4] 贾龙,胡泽春,宋永华,等.高速路网上电动汽车充电站布点优化[J].电力系统自动化,2015,39(15):82-89.DOI:10.7500/AEPS20140528007. JIA Long, HU Zechun, SONG Yonghua, et al. Planning of electric vehicle charging stations in highway network[J]. Automation of Electric Power Systems, 2015, 39(15): 82-89. DOI: 10.7500/AEPS20140528007. [5] 刘耀辉.城市电动汽车充电站选址与定容方法研究[D].上海:上海电力学院,2016. [6] 宋阳.电动汽车充电站布局优化研究[D].成都:西南交通大学,2016. [7] 刘锴,李昂,孙小慧.电动汽车充电站布局优化研究[J].城市交通,2016,14(4):64-69. LIU Kai, LI Ang, SUN Xiaohui. Optimizing spatial distribution of EV charging stations [J]. Urban Transportation of China, 2016, 14(4): 64-69. [8] 徐青山,蔡婷婷,刘瑜俊,等.考虑驾驶人行为习惯及出行链的电动汽车充电站站址规划[J].电力系统自动化,2016,40(4):59-65.DOI:10.7500/AEPS20150704006. XU Qingshan, CAI Tingting, LIU Yujun, et al. Location planning of charging stations for electric vehicles based on drivers’ behaviours and travel chain[J]. Automation of Electric Power Systems, 2016, 40(4): 59-65. DOI: 10.7500/AEPS20150704006. [9] 陈静鹏,艾芊,肖斐.基于用户出行需求的电动汽车充电站规划[J].电力自动化设备,2016,36(6):34-39. CHEN Jingpeng, AI Qian, XIAO Fei. EV charging station planning based on travel demand[J]. Electric Power Automation Equipment, 2016, 36(6): 34-39. [10] 温剑锋,陶顺,肖湘宁,等.基于出行链随机模拟的电动汽车充电需求分析[J].电网技术,2015,39(6):1477-1484. WEN Jianfeng, TAO Shun, XIAO Xiangning, et al. Analysis on charging demand of EV based on stochastic simulation of trip chain[J]. Power System Technology, 2015, 39(6): 1477-1484. [11] 党杰,汤奕,宁佳,等.基于用户意愿和出行规律的电动汽车充电负荷分配策略[J].电力系统保护与控制,2015,43(16):8-15. DANG Jie, TANG Yi, NING Jia, et al. A strategy for distribution of electric vehicles charging load based on user intention and trip rule[J]. Power System Protection and Control, 2015, 43(16): 8-15. [12] 付凤杰,龚越,王殿海,等.基于高清智能卡口路段行程时间的数据质量分析[J].浙江大学学报(工学版),2016,50(9):1761-1767. FU Fengjie, GONG Yue, WANG Dianhai, et al. Data quality analysis of link travel time based on HD smart gate[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(9): 1761-1767. [13] MA D, LUO X, LI W, et al. Traffic demand estimation for lane groups at signal-controlled intersections using travel times from video-imaging detectors[J]. IET Intelligent Transport Systems, 2017, 11(4): 222-229. [14] SUN Y, ZHU H, ZHOU X, et al. VAPA: vehicle activity patterns analysis based on automatic number plate recognition system data[J]. Procedia Computer Science, 2014, 31: 48-57. [15] TU W, LI Q, FANG Z, et al. Optimizing the locations of electric taxi charging stations: a spatial-temporal demand coverage approach[J]. Transportation Research Part C, 2016, 65: 172-189. [16] 刘自发,张伟,王泽黎.基于量子粒子群优化算法的城市电动汽车充电站优化布局[J].中国电机工程学报,2012,32(22):39-45. LIU Zifa, ZHANG Wei, WANG Zeli. Optimal planning of charging station for electric vehicle based on quantum PSO algorithm[J]. Proceedings of the CSEE, 2012, 32(22): 39-45. [17] YANG J, DONG J, HU L. A data-driven optimization-based approach for siting and sizing of electric taxi charging stations[J]. Transportation Research Part C: Emerging Technologies, 2017, 77: 462-477. [18] XI X, SIOSHANSI R, MARANO V. Simulation-optimization model for location of a public electric vehicle charging infrastructure[J]. Transportation Research Part D: Transport & Environment, 2013, 22(4): 60-69. [19] GHAMAMI M, ZOCKAIE A, YU N. A general corridor model for designing plug-in electric vehicle charging infrastructure to support intercity travel[J]. Transportation Research Part C: Emerging Technologies, 2016, 68: 389-402. [20] 付凤杰.基于自动车牌识别数据的城市道路行程时间估计[D].杭州:浙江大学,2017.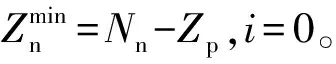
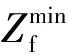
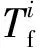
3.2 充电站运营商利润
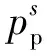
3.3 约束条件
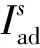
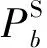
3.4 优化模型
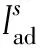
3.5 模型求解
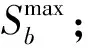
4 数值分析
4.1 案例基本信息
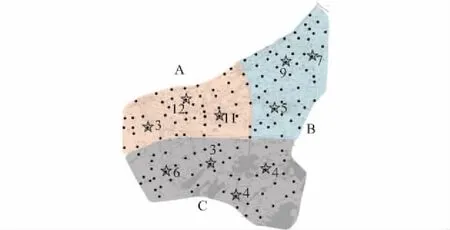
4.2 优化方案
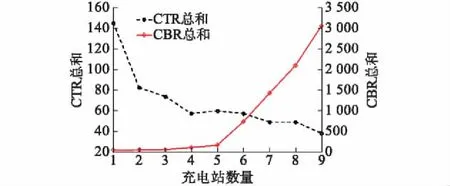
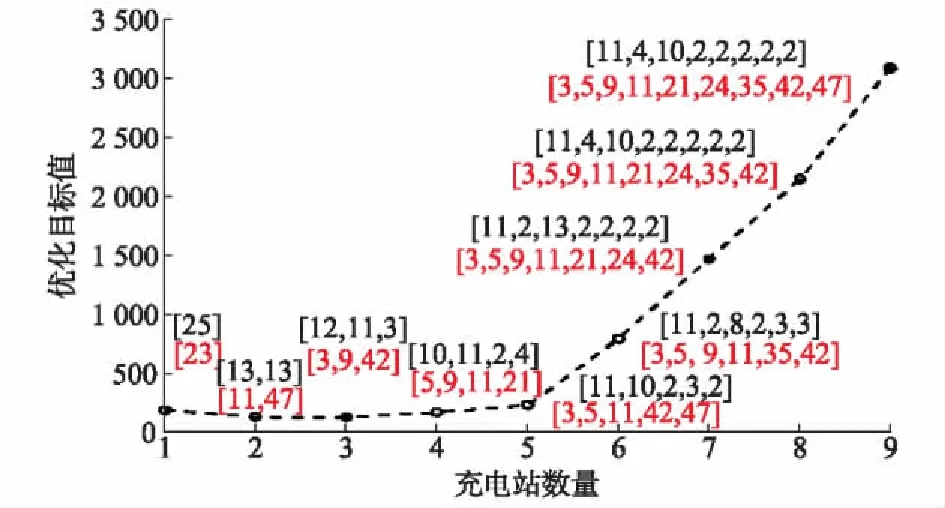
4.3 工作日/非工作日布设方案对比分析
4.4 电池技术发展对预测方案的影响
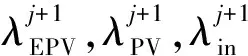
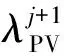
5 结语
