具有电力需求预测更新的智能电网实时定价机制

代业明, 高红伟, 高 岩, 袁光辉

(1. 青岛大学数学与统计学院, 山东省青岛市 266071; 2. 上海理工大学管理学院, 上海市 200093;3. 上海财经大学信息管理与工程学院, 上海市 200433)

0 引言

智能电网能够通过先进双向通信技术,鼓励用户参与需求侧管理(demand side management,DSM),并运用激励机制和价格响应发挥需求侧的电力市场作用[1-2]。基于价格的需求响应是指用户响应市场电价变化而做出的电力需求调整,是需求响应的关键方法,主要包括分时电价、尖峰电价和实时定价(real-time pricing,RTP)等[3]。随着先进智能计量技术的快速发展,能够反映用户实时电力需求的RTP是适合竞争性电力市场最直接和有效的工具,是近几年智能电网领域的研究热点之一。

国内外关于RTP的研究如下:①研究用户如何对RTP自动响应,以较低费用达到理想满意程度[4];②研究RTP如何由售电商制定,而不考虑用户对预测价格的潜在反应[5-6];③使用优化理论研究整个社会福利最大化的电力供需匹配问题[7-9];④博弈方法被用于研究RTP问题[10]。已有采用博弈方法来研究RTP的文献大多考虑用户之间或供电商之间的同层次竞争[4,10-12],而现实中的电力系统则呈现出多层次结构特征。如文献[13]将售电商与用户之间的策略互动生成Stackelberg博弈研究RTP问题,但售电商和用户均被视为单一形式;文献[14-17]均通过建立不同的博弈模型研究多个供电商与多个用户之间的需求响应和RTP问题,并分别从信息完全或带有个人隐私角度进行了分析,但都基于历史数据预先预测用户电力需求信息,忽视了用户电力需求信息存在实时更新的事实。特别是随着智能电网技术的进步和社会经济发展,能源需求信息变动更加频繁,受传输时间滞后以及设备故障等不确定性因素影响,可能导致实时用电需求信息传递的延迟[18],从而影响电力调度与调频以至于对电力供求平衡带来不良影响。

为了维护电力系统的稳定性和精确估计用户实时用电信息,电力需求信息预测实时更新可以作为一种重要手段加入智能电网RTP决策中。目前常用的需求信息更新方法多采用贝叶斯更新方法[19],常用于供应链网络和最优存储领域[20-22],然而在智能电网领域特别是需求侧管理中尚无相关文献。

本文通过将贝叶斯更新方法引入智能电网实时电力需求预测中,使用调整后的用户社会福利函数,并根据总收益与总成本之差构造售电商利润函数,讨论当系统存在电力需求信息预测更新且售电商与用户可以共享观测信息时,通过观察当前时段实际用电数据,运用贝叶斯更新方法对已有先验信息进行更新,修正电力需求分布,最后建立博弈模型研究RTP问题。

1 系统模型

考虑由一个售电商和多个用户组成的智能电网系统。售电商从电力现货市场购买电力然后卖给用户,每个用户安装有一个能量管理控制器(energy management controller,EMC)来通过双向连通网络与售电商进行实时互动,合理安排电力使用。假设一个运行时间循环被分成K个时段,在每个时段t(t∈{1,2,…,K}中,售电商接受用户的电力需求并将实时价格发送给用户的EMC,一般这里取K=24,即每个时段为1 h。

电力用户集合用RN={1,2,…,N}表示,售电商制定有利于自己利益的价格,用pt来表示其在第t个时段的报价,N个用户在此时段的电力实时需求可用xt=(xt,1,…,xt,i,…,xt,N)表示。售电商根据服务的全部用户实时电力需求采购电力并制定使自己利润最大化的价格,并告之所有用户。本文假定售电商在电力批发市场能够采购到足够的电力供用户使用。

1.1 用户的效用函数

用户i的效用体现其满意度大小,应为关于用电量的凹函数,且具有边际收益递减特征,于是选择二次函数作为效用函数[4-5,14]：

(1)

式中:ωt,i>0为随用户和时段变化的参数;α为事先给定的参数。

定义用户i的社会福利函数[4-5]如下:

Uc,i(xt,i)=γWi(xt,i,ωt,i)-ptxt,i

(2)

式中:γ为一个正参数。

1.2 售电商的利润函数

售电商的收益来自t时段的电价和所有用户的用电量,于是售电商利润函数[4-5]为:

(3)

式中:pH为售电商的单位购电成本,为定值。售电成本忽略不计。

2 贝叶斯更新方法

在信息化大数据时代,信息的实时更新与反馈成为竞争的关键要素,贝叶斯方法[19]是解决上述电力需求信息不确定问题的一种有效方法。与传统电力系统电力需求预测方法不同,贝叶斯方法基于先验信息和有限的样本信息不断更新当前的需求信息,降低预测误差。近年来,贝叶斯更新方法被众多国内外学者所青睐。

2.1 电力实时需求的贝叶斯更新方法

在电力市场中,假设电力需求是一个随机变量X,期望为E,E也是一个随机变量,其概率分布密度函数fE(e)已知,称之为电力需求期望的先验概率密度函数,表示售电商对于电力市场中电力需求期望的了解程度,例如,当知道电力市场的需求期望接近于某一固定值e时,那么E就极可能是一个具有较小方差且服从正态分布的随机变量,通常需求期望E的常见分布有均匀分布、正态分布等[23-24]。当电力市场需求期望E给定,即E=e时,电力市场需求变量X的条件概率分布fX|E=e(x)为一个已知的分布,其常用形式有泊松分布、正态分布、伽马分布等[23-24]。

若电力需求期望E的概率密度函数fE(e)及需求X的条件概率密度函数fX|E=e(x)均已知时,即可求出电力需求X的先验概率密度函数为:

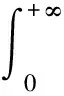
(4)

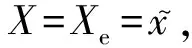
(5)

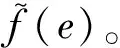
(6)

此即随机电力需求X的后验概率密度函数。

2.2 电力需求预测的贝叶斯更新过程

由2.1节可以得知,fE(e)和fX|E=e(x)均为正态密度函数,且fE(e)～N(μ,τ2),fX|E=e(x)～N(e,σ2),则电力需求X的先验概率密度函数为：

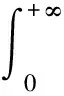
(7)

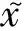
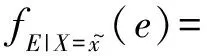
(8)

最后，求出电力需求X的后验概率密度函数为[25]:

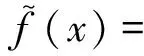
(9)

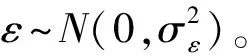
3 需求预测更新下博弈模型的生成与分析

主从博弈模型[26]已被广泛应用于存在不同层次结构的竞争性决策中。售电商首先报价,然后用户基于电价做出自己的决策,因此将用户和售电商之间的策略互动行为生成为一主多从博弈模型进行分析。

3.1 博弈模型的建立

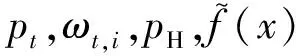
电力需求信息预测更新后售电商的期望利润函数为:

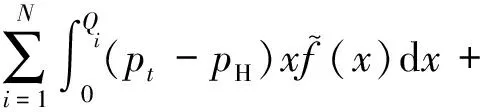
(10)

用户i的期望福利函数为:

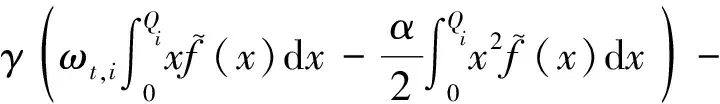
(11)

易知Uc,i为关于Qi的凹函数。

生成的博弈模型如下:

(12)

(13)

3.2 博弈求解及分析

售电商作为领导者首先确定电价pt,用户作为从属者确定各自最优用电量Qi,这是典型的二层规划问题。由式(11)可知,式(13)所示问题实际是一个凸优化问题,因此其解存在且唯一,得到如下命题。

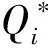
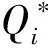
定理1电力需求预测更新下生成的主从博弈模型均衡解存在。

证明根据命题1可知下层用户间非合作博弈唯一的纳什均衡解存在,将其代入上层优化问题后,由命题2可知解也存在,于是该主从博弈模型的均衡解存在。

考虑下层用户一阶最优性条件可得∂Uc,i/∂Qi=0,即

(14)

可得下层对于上层决策变量的最优反应函数为:

(15)

式中:

将式(15)代入式(10)后,由售电商期望利润最大化一阶最优性条件dUd/dpt=0,解得:

(16)

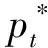
(17)

于是存在电力需求预测更新的最优实时电价与用户的最优用电量被确定。

4 无电力需求更新下博弈模型的生成与分析

无电力需求预测信息更新时,售电商作为主从博弈模型的领导者率先报价pt,用户作为从属者决定用电量xt,i,由前文可知售电商的利润函数为:

(18)

用户的社会福利函数为:

Uc,i(xt,pt)=γWi(xt,i,ωt,i)-ptxt,i

(19)

博弈模型生成如下:

(20)

(21)

求解可得:

(22)

以上即是不存在电力需求信息预测更新时,得到的t时段最优实时电价与用户电力需求量。

5 数值仿真分析

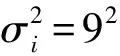
首先,考察随着购电成本pH增加时,在有无电力需求信息更新时的最优实时电价、用户社会总福利和售电商利润的变化趋势图。由图1可见,随着购电成本pH的增加,售电商最优实时电价随之增加,此时带来用户社会总福利降低。但是对比发现,在本文提出的具有需求信息预测更新的RTP机制下,当实时电价相同时用户有着更高的社会总福利,用户能够以较低的电价购买和满足电力需求,从而可以给用户带来更大的满意度,这正是智能电网实施需求侧管理的目的所在,有利于促进用户更好地参与需求侧管理。同时也发现,鉴于上述分析,图2中当电价较低时,用户电力需求增加,导致售电商利润增大,说明考虑电力需求预测信息更新的RTP机制对售电商更有利。

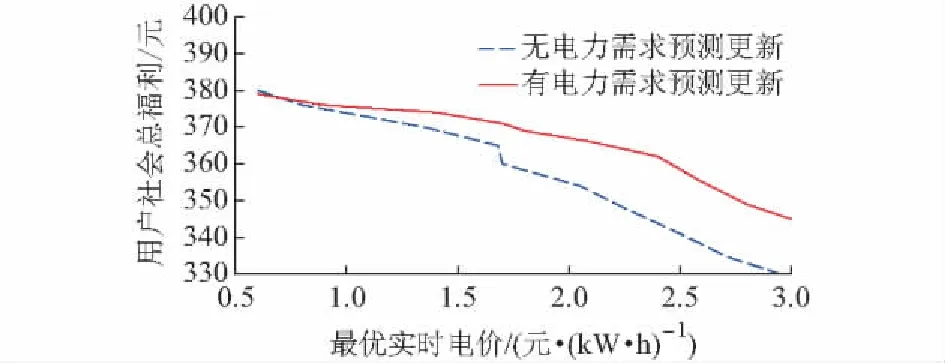
图1 有无电力需求信息更新时售电商实时电价与用户社会总福利Fig.1 Real-time price of retailer and total social welfare of users with and without information updates of power demand

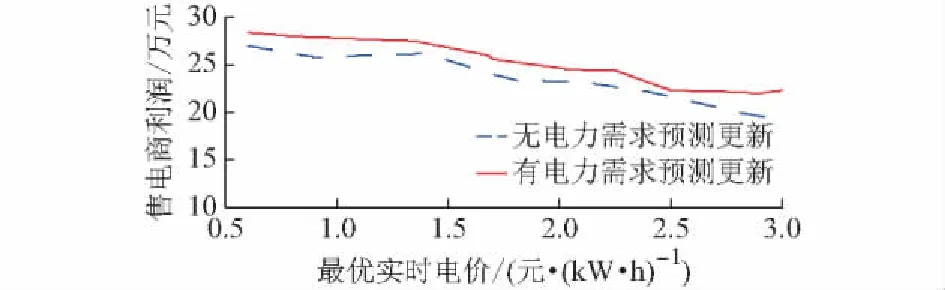
图2 有无电力需求信息更新时售电商实时电价与利润Fig.2 Real-time price and profit of retailer with and without information updates of power demand

为了分析多阶段下考虑电力需求预测信息更新带来的影响,设定pH=0.5,其余参数保持不变,考察24 h下售电商实时电价、利润以及全部用户社会总福利对比情形。由图3可知,在24 h内,考虑电力需求预测更新下的实时电价总体相对较低,可见信息的更新总体有利于实时电价的降低,但是通过图4和图5可知,其增加了售电商的利润及用户社会总福利,电力需求信息预测更新在多时段能给用户带来较大满意度且可持续,从而证明了本文所建模型的有效性与合理性。

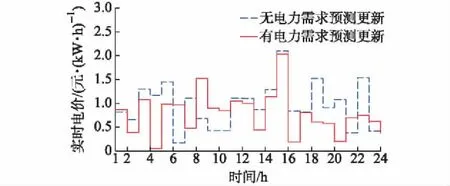
图3 有无电力需求信息更新时24 h实时电价Fig.3 Real-time price in 24 h with and withoutinformation updates of power demand

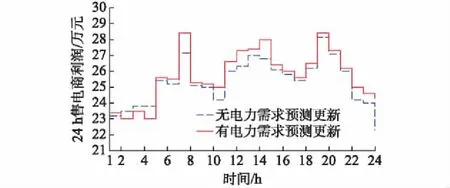
图4 有无电力需求信息更新时24 h售电商利润Fig.4 Profit of retailer in 24 h with and without information updates of power demand

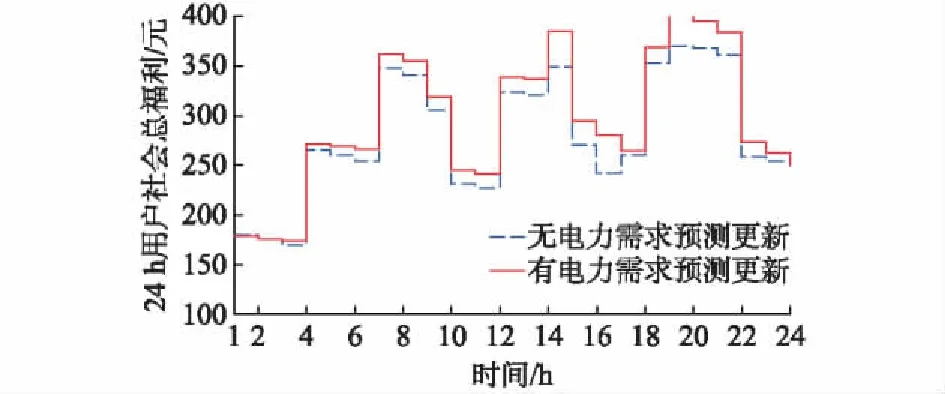
图5 有无电力需求信息更新时24 h用户社会总福利Fig.5 Total social welfare of users in 24 h with and without information updates of power demand

6 结语

本文针对智能电网环境研究了电力需求预测信息更新情形下基于主从博弈的RTP定价机制问题。通过对比研究和数值仿真分析,发现电力需求预测信息更新更有利于促使用户参与需求侧管理,提高用户满意度和售电商利润。售电商应该从定价策略以及与用户的交互作用中,加强对用户需求响应的研究,充分发挥电力需求信息预测更新的实践作用。随着新的预测技术的发展,用更加精确的预测技术代替贝叶斯预测更新方法会更有利于RTP机制的制定。

从电力市场竞争的角度去探究,本文还可以做更多的拓展,比如考虑电力需求信息预测更新下多个售电商之间的寡头博弈模型,寡头之间预测信息共享或不共享以及非合作下分别探讨电力市场中的实时电价,能够使得研究更加贴近实际。作为电力市场中的三类主体,售电商、发电商与用户之间的相互博弈能够对完善电力调度和电力的区域分配起到指导作用。

本文研究获得青岛市博士后应用研究项目(2016033)的资助,谨此致谢。

参考文献

[1] YAO Liangzhong, YANG Bo, CUI Hongfen, et al. Challenges and progresses of energy storage technology and its application in power systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(4): 519-528.

[2] 李立浧,张勇军,陈泽兴,等.智能电网与能源网融合的模式及其发展前景[J].电力系统自动化,2016,40(11):1-9.DOI:10.7500/AEPS20150912002.

LI Licheng, ZHANG Yongjun, CHEN Zexing, et al. Merger between smart grid and energy-net: mode and development prospects[J]. Automation of Electric Power Systems, 2016, 40(11): 1-9. DOI: 10.7500/AEPS20150912002.

[3] CARAMANIS M C, BOHN R, SCHWEPPE F C. Optimal spot pricing: practice and theory[J]. IEEE Transactions on Power Apparatus and Systems, 1982, 10(9): 3234-3245.

[4] MOHSENIAN-RAD A H, WONG V W S, JATSKEVICH J, et al. Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid[J]. IEEE Transactions on Smart Grid, 2010, 1(3): 320-331.

[5] 代业明,高岩.基于智能电网需求侧管理的多售电商实时定价策略[J].中国电机工程学报,2014,34(25):4244-4249.

DAI Yeming, GAO Yan. Real-time pricing strategy with multi-retailers based on demand-side management for the smart grid[J]. Proceedings of the CSEE, 2014, 34(25): 4244-4249.

[6] 张晓萱,薛松,杨素,等.售电侧市场放开国际经验及其启示[J].电力系统自动化,2016,40(9):1-8.DOI:10.7500/AEPS20151128001.

ZHANG Xiaoxuan, XUE Song, YANG Su, et al. International experience and lessons in power sales side market liberalization[J]. Automation of Electric Power Systems, 2016, 40(9): 1-8. DOI: 10.7500/AEPS20151128001.

[7] SAMADI P, MOHSENIAN-RAD H, SCHOBER R, et al. Advanced demand side management for the future smart grid using mechanism design[J]. IEEE Transactions on Smart Grid, 2012, 3(3): 1170-1180.

[8] 舒畅,钟海旺,夏清.基于优化理论市场化的日前电力市场机制设计[J].电力系统自动化,2016,40(2):55-62.DOI:10.7500/AEPS20150922003.

SHU Chang, ZHONG Haiwang, XIA Qing. Day-ahead electricity market design based on market interpretation of optimization theory[J]. Automation of Electric Power Systems, 2016, 40(2): 55-62. DOI: 10.7500/AEPS20150922003.

[9] 曾鸣,杨雍琦,向红伟,等.计及需求侧响应的电力系统鲁棒优化规划模型[J].电力系统自动化,2016,40(17):137-145.DOI:10.7500/AEPS20150615001.

ZENG Ming, YANG Yongqi, XIANG Hongwei, et al. Robust optimization planning model of power system considering demand response[J]. Automation of Electric Power Systems, 2016, 40(17): 137-145. DOI: 10.7500/AEPS20150615001.

[10] SAAD W, HAN Z, POOR H V, et al. Game theoretic methods for the smart grid[J]. IEEE Signal Processing Magazine, 2012, 29(5): 86-105.

[11] IBARS C, NAVARRO M, GIUPPONI L. Distributed demand management in smart grid with a congestion game[C]// IEEE International Conference on Smart Grid Communications, October 4-6, 2010, Gaithersburg, USA: 495-500.

[12] DAI Yeming, GAO Yan. Real-time pricing decision based on leader-follower game in smart grid[J]. Journal of Systems Science and Information, 2015, 3(4): 348-356.

[13] 代业明,高岩.具有多类资源多类用户智能电网实时定价决策[J].系统工程理论与实践,2015,35(9):2315-2323.

DAI Yeming, GAO Yan. Real-time pricing decision-making in smart grid with multi-type users and multi-type power sources[J]. Systems Engineering—Theory & Practice, 2015, 35(9): 2315-2323.

[14] CHAI Bo, CHEN Jiming, YANG Zaiyue, et al. Demand response management with multiple utility companies: a two-level game approach[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 722-731.

[15] KAMYAB F, AMINI M, SHEYKHHA S, et al. Demand response program in smart grid using supply function bidding mechanism[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1277-1284.

[16] MAHARJAN S, ZHU Quanyan, ZHANG Yan, et al. Dependable demand response management in the smart grid: a Stackelberg game approach[J]. IEEE Transactions on Smart Grid, 2013, 4(1): 120-132.

[17] 代业明,高岩,高红伟,等.智能住宅小区的需求响应主从博弈模型[J].电力系统自动化,2017,41(15):88-94.DOI:10.7500/AEPS20161122008.

DAI Yeming, GAO Yan, GAO Hongwei, et al. Leader-follower game model for demand response in smart residential grid[J]. Automation of Electric Power Systems, 2017, 41(15): 88-94. DOI: 10.7500/AEPS20161122008.

[18] 代业明,高红伟,高岩.考虑信息延迟的智能电网实时定价和算法[J].工业工程与管理,2017,22(2):96-102.

DAI Yeming, GAO Hongwei, GAO Yan. Real-time pricing and algorithm considering information delay in smart grid [J]. Industrial Engineering and Management, 2017, 22(2): 96-102.

[19] CLAYTON D, KALDOR J. Empirical Bayes estimates of age-standardized relative risks for use in disease mapping[J]. Biometrics, 1987, 43(3): 671-681.

[20] DING Xiaomei, PUTERMAN M L, BISI A. The censored newsvendor and the optimal acquisition of information[J]. Operations Research, 2002, 50(3): 517-527.

[21] 宋华明,杨慧,罗建强,等.需求预测更新情形下的供应链Stackelberg博弈与协调研究[J].中国管理科学,2010,18(4):86-92.

SONG Huaming, YANG Hui, LUO Jianqiang, et al. Supplier buyer Stackelberg game and supply chain coordination with demand forecast updating[J]. Chinese Journal of Management Science, 2010, 18(4): 86-92.

[22] 李娟,黄培清.基于长期或短期战略下的两期供应链合同分析[J].管理科学学报,2010,13(2):33-40.

LI Juan, HUANG Peiqing. Analysis of two-period supply chain contracts based on strategies of long-term or short term[J]. Journal of Management Science in China, 2010, 13(2): 33-40.

[23] MILTENBURG J, PONG H C. Order quantities for style goods with two order opportunities and Bayesian updating of demand: Part Ⅰ no capacity constraints[J]. International Journal of Production Research, 2007, 45(7): 1643-1663.

[24] IYER A V, BERGEN M E. Quick response in manufacturer-retailer channels[J]. Management Science, 1997, 43(4): 559-570.

[25] BERGER M, HAIMOWITZ A, VAN TOSH A, et al. Quantitative assessment of pulmonary hypertension in patients with tricuspid regurgitation using continuous wave Doppler ultrasound[J]. Journal of the American College of Cardiology, 1985, 6(2): 359-365.

[26] MYERSON R B, Game theory: analysis of conflict [M]. Boston, USA: Harvard University Press, 1991.