含新能源接入的区域电网低碳电力调度方法
2018-06-21徐青山蒋贤强娄藕蝶
黄 煜, 徐青山, 蒋贤强, 娄藕蝶, 蒋 菱
(1. 东南大学电气工程学院, 江苏省南京市 210096; 2. 国网天津市电力公司电力科学研究院, 天津市 300384)
0 引言
近年来,随着能源需求的持续增长,环境问题日益凸显。推行节能减排,发展低碳经济是应对当前气候变暖、雾霾危机的有效措施,也是可持续发展的必由之路。目前,中国电力行业作为CO2排放大户,占全国碳排放总量的比重超过40%。因此,在电网层面,建立高效、完善的碳排放管理机制,发展低碳电力潜力巨大,受到社会广泛关注[1-3]。
当前的减排措施可以分为两大类:发电侧可再生能源的接入及需求侧管理[4-5]。由于电力行业的碳排放量主要源自发电侧,再加上与需求侧资源频繁进行交互会带来额外费用,因而积极发展以风电光伏为代表的清洁能源,在综合考虑环境因素、电网安全性和经济性的基础上,尽量提高发电侧新能源并网比重,制定最优的低碳调度方案无疑是更好的选择。对于含新能源发电的优化调度问题,国内外学者已经做了大量的研究。文献[6]在传统的低碳经济调度模型基础上考虑了风电预测误差的影响。文献[7]中的调度模型计及了环境约束,并重点分析了碳补集电厂的运行特性和经济效益。另外,文献[8]还制定了风—火电系统联合协调调度方案。
尽管新能源在节能减排方面作用显著,其出力的间歇性和波动性也会给电网带来诸多不确定因素,进而降低整个系统的安全性和可靠性。概率潮流是电力系统不确定性分析的重要工具,其通过概率统计方法得到系统潮流的分布信息,能够计及各种随机因素场景,全面反映电网的运行工况,便于调度人员发现系统薄弱环节和潜在风险[9]。文献[10-11]将概率潮流方法分为三类:模拟法、近似法和解析法。以蒙特卡洛仿真(Monte Carlo simulation,MCS)为代表的模拟法原理简单、通用性强且精度最高,但计算规模过大、耗时长。近似法包括点估计法[12]、一次二阶矩法等,以及解析法中的半不变量法(cumulant method,CM)[13-14]等计算速度快,但局限性较大,精度难以保证,且易受随机变量类型及系统维数的制约。目前,求解含随机输入变量或机会约束的概率最优潮流问题主要以MCS和点估计法为主,难以同时兼顾计算精度和效率。
基于上述分析,本文引入区域碳排放量平衡的概念[15],通过控制不同区域之间的碳排放量实现整个地区的碳排放平衡。采用基于随机响应面法(stochastic response surface method,SRSM)的概率潮流,得到含多个关联新能源电站的电网潮流分配情况。提出带模糊满意度决策的改进帝国主义竞争算法(imperialist competitive algorithm,ICA)求解文中建立的多目标优化模型,并根据系统运行人员的不同需求得到折中调度方案。
1 考虑区域碳排放平衡的低碳电力调度模型
1.1 目标函数
传统的低碳优化调度模型包含2个优化目标:成本最低及碳排放总量最少。在接入有风电、光伏等新能源的系统中,其函数表达式如下。
1)平均发电成本
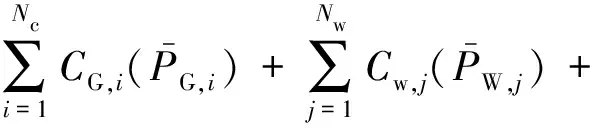
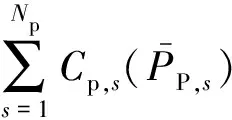
(1)
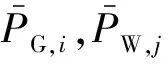
2)平均碳排放量
(2)
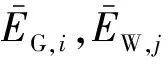
为了实现不同区域间的碳排放量平衡,还要最小化式(3)的目标函数。
3)平均区域碳排放差异量
(3)
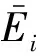
1.2 约束条件
1)功率平衡约束
(4)
式中:PG,i,PW,i,PP,i,PL,i分别为节点i上所有火电机组、风电场、光伏电站及负荷的有功出力;QG,i,QW,i和QL,i分别为火电机组、风电场、负荷的无功功率,光伏电站的无功功率为0;Vi为节点i的电压幅值;θij为节点i,j之间的相角差;Nb为节点个数;Gij和Bij分别为节点i,j之间的电导和电纳。
2)火电机组出力约束
(5)
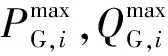
3)节点电压约束
(6)
4)支路功率约束:
(7)
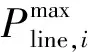
事实上,本文的区域电网低碳调度模型实质是一个多目标概率最优潮流问题,可分为两个部分:含新能源的概率潮流和多目标优化。概率潮流用于处理约束条件中含机会约束的不等式(式(6)和式(7)),将越限部分作为惩罚项添加到原目标函数中,再通过多目标优化算法进行求解。需要说明的是,在实际工程中,整个电网的各个区域应由调度部门事先根据地理位置进行合理划分,尽量保证各区域间的环境、经济及负荷水平基本一致,避免由于划分不当,不同区域碳排放量差异过大,导致最终的优化结果失去意义。
2 基于随机响应面法的概率潮流
2.1 SRSM简介
由于上述模型中含有随机状态量(Vi,Pline,i)的机会约束,需要先求得各节点电压及支路功率的概率分布,本节采用文献[16]提出的基于SRSM的概率潮流方法,其本质为利用多项式混沌展开建立系统响应的概率模型。相较于常用的MCS、点估计法等,SRSM只需对少量配置点进行确定性潮流计算,极大提高了计算效率,同时,其避免了解析法[13-14]中的线性化假设、级数逼近和难以计及相关性等局限,从而保证了较高的计算精度。文中首次将SRSM嵌入于概率最优潮流问题的求解中,具体包含以下3个步骤。
1)随机变量的标准化,设PW,PP和PL分别表示风电、光伏和负荷的有功出力,根据各自的功率特性服从不同的概率分布。利用边缘变换[10]可以将系统所有输入变量转换为只服从标准正态分布的随机变量:
(8)
式中:n为系统输入随机变量个数;Xi为X=[PW,PP,PL]中第i个输入变量;ξi为标准正态变量;Fi(·)和Φ(·)分别为Xi和ξi的累积分布函数(CDF)。
2)输出响应的多项式混沌展开,当输入变量通过式(8)全部表示为一系列标准正态变量ξ=[ξ1,ξ2,…]后,系统的输出响应模型可近似展开为:
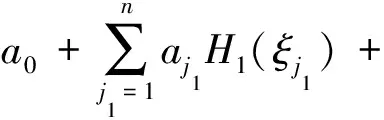
(9)
式中:a0,aj1,aj1j2和aj1j2j3为待定系数;ξj1,ξj2和ξj3均为标准正态变量;Hm为m阶Hermite多项式。
一般而言,m取2或3足以满足工程应用下的精度要求。为方便起见,文中取m=2,则输出变量Y的二阶展开式Y2为:
(10)
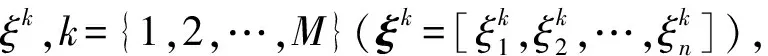
2.2 相关性处理
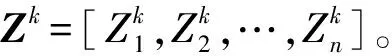
Zk=Lξkk=1,2,…,M
(11)
式中:L为下三角矩阵,可通过对Z的协方差矩阵RZ进行Cholesky分解得到。
RZ=LLT
(12)
式中:RZ由输入随机变量X的协方差矩阵RX按文献[17]中的经验公式修正后得到。
第2步则是对中间变量Z按式(8)作边缘变换,得到服从给定分布的关联输入变量X的样本点,继而求得输出响应样本Yk和未知系数ai。
2.3 整体流程
综合以上步骤,基于SRSM含关联输入变量的概率潮流整体流程如下。
1)输入电网参数、网络拓扑结构及系统输入随机变量(包括风电场、光伏电站和负荷)的概率分布参数。
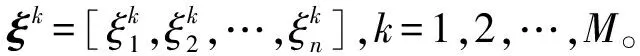
3)采用Nataf变换将所有配置点从标准正态空间转换到原始空间,得到一系列关联输入变量的样本点。
4)利用Matpower工具箱对每个输入样本点进行确定性潮流计算,得到对应的输出响应量Y(包括节点电压、支路功率、网损等)的样本点。
5)通过配置点及其对应的输出响应样本求解多项式的未知系数ai,得到输出变量Y的多项式混沌展开表达式。
3 多目标优化模型的求解
对于文中第1节建立的多目标区域碳排放模型,传统的求解方法有非支配排序遗传算法(non-dominated sorting genetic algorithm, NSGA)及其各种改进版本。然而,遗传算法(GA)存在固有收敛速度慢且易陷入局部最优解的缺陷,因此,本文借鉴免疫算法的思想,提出一种带克隆进化算子的改进ICA,并在此基础上,采用交互式模糊满意度决策方法得到模型的“最优解”。
3.1 多目标改进ICA
ICA是由Atashpaz-Gargari和Lucas受帝国主义殖民竞争机制启发于2007年提出的一种智能优化算法[18]。类比GA中的染色体,ICA的主体是国家(分为帝国主义国家和殖民地),其通过帝国内部的同化改革进行局部搜索,利用帝国间的竞争机制实现全局寻优,两步协同配合,极大地提升了寻优效率,相较于常用的GA、粒子群算法(particle swarm optimization,PSO)等,普遍收敛速度更快。但原始的ICA(OICA)过程中,由于帝国之间缺乏有效的信息交互,每次迭代中帝国势力变化不明显。为此,我们引入克隆进化算子,对势力较强的国家进行克隆繁殖,并通过克隆群体的高频变异和随机交叉,以取代势力较弱的国家,从而能够有效引导算法向最优解方向搜索,提高全局寻优能力。具体改进措施如下。
1)克隆
将当前生成的帝国主义国家按势力(适应度)大小降序排列,每个国家分别克隆NC,i次,势力越大则克隆群体个数越多。
NC,i=floor(λNcol,i)
(13)
式中:floor(·)为向下取整函数;λ为克隆系数,其值决定了克隆群体的大小,太小会使克隆效果不明显,太大又会影响收敛速度;Ncol,i为第i个帝国主义国家的殖民地个数。
2)变异
对第i个帝国的克隆群体Xclo,i进行变异,产生新的变异群体Hi。
(14)
(15)
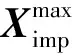
3)交叉
将变异群体Hi随机划分为4个一组,每组进行交叉计算,即
Ki=Hi,1-Hi,2+Hi,3-Hi,4
(16)
4)选择
取Ki和Hi中势力最大的m个克隆变异个体取代当前势力最小的m个帝国主义国家。
上述改进方法中的克隆进化算子虽然显著加快了帝国竞争与合并的速度,却也增加了ICA陷入局部最优的风险。因此,在每次迭代中使帝国以概率pm进行合并,适当减小pm能够解决算法易早熟收敛的问题,进一步提升ICA的整体性能。参照NSGA过程,可以相应得到一种多目标改进ICA,其具体步骤如下。
步骤1:输入电网参数,各随机变量的分布参数及改进ICA的参数(包括初始国家个数Npop、最大迭代次数kmax等)。
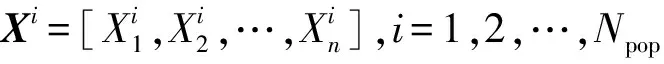
步骤3:进行原始的ICA操作,包括帝国间的同化、革命、竞争及合并过程[18-19]。
步骤4:采用克隆进化算子对帝国间进行操作。
步骤5:调整新的帝国主义国家使其满足式(5)的约束并进行概率潮流计算。根据式(6)和式(7)的机会约束,引入惩罚项JV和JP。
(17)
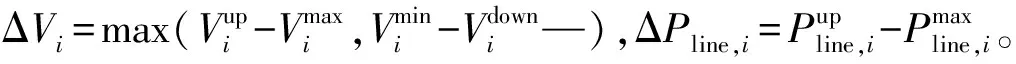
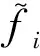
(18)
式中:μ1和μ2为惩罚项系数。
步骤6:对于每个国家计算新的目标函数值,利用Pareto支配理论从帝国主义国家中选择出非劣解集。
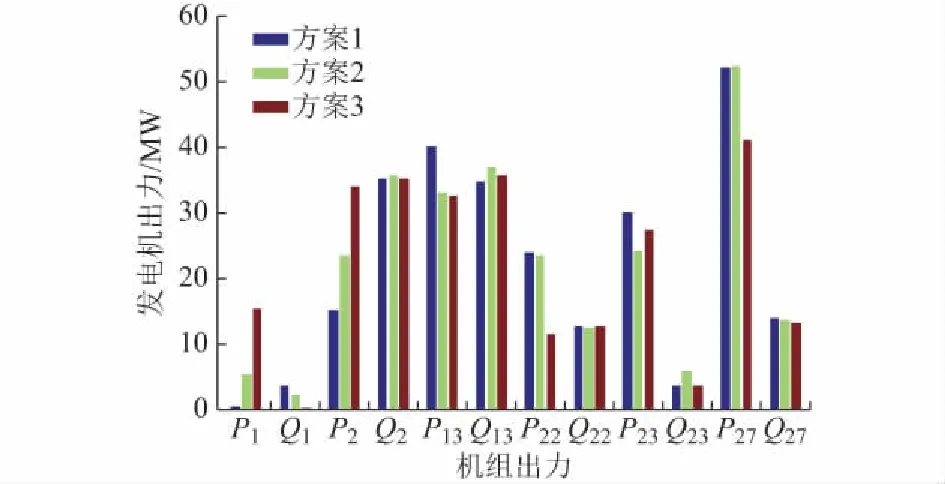
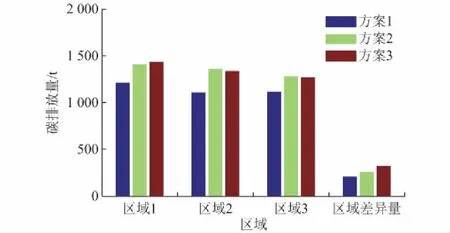
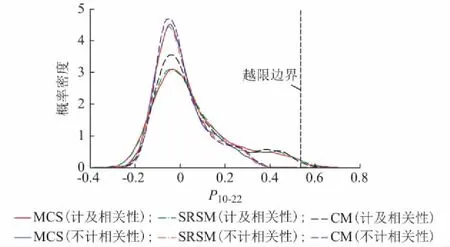
步骤7:检验算法终止判据,若迭代次数k 为了找出一个折中的“最佳”方案,本文采用文献[20-21]中的交互式模糊满意度决策方法,首先构造表征目标函数满意度的logistic隶属度函数(区间[0,1]的单调减函数),其值能够量化决策者的满意度,隶属度越大表示越倾向于接受。 i=1,2,3;X∈Ω (19) 式中:Ω为X的可行域;U(·)为线性归一化函数;εi和χi均为Lfi的参数,用于确定fi的模糊值及中间点的大小,这里取εi=10,χi=0.5。 根据决策者的主观需求,定义每个目标函数的参考隶属度Lr,i,其值取区间[0,1]内的任意实数,可以表示相应目标函数的重要程度,Lr,i越大,fi越重要。通过求解式(20)的极小—极大化问题,可以得到基于决策者需求的最优解,即 min{max(|Lr,i-Lfi(X)|)}i=1,2,3;X∈Ω (20) 值得注意的是,文献[21]证明了若X*为式(20)的最优解,其也必为多目标问题(式(1)至式(7))的一个非劣解。因此,可直接用3.1节所求得的Pareto最优解集替代可行域Ω,从中选出“最佳”决策方案。 本文在主频为2.63 GHz,运行内存为2 GB的intel i3个人计算机上,利用MATLAB 2014b仿真平台分别对Matpower 30 节点系统和江苏省某区域实际电网进行算例测试。 附录A给出了Matpower 30节点测试系统的网络拓扑,系统内含6台火电机组、41条支路、20个负荷节点并且分为3个区域。假设所有机组均为火电机组,具体运行参数见附录B。各负荷节点的功率参数为一天24 h的平均负荷,其随机波动服从正态分布,标准差为相应均值的15%。为简化计算,假设负荷的功率因数角恒定,cosφ=0.95。 在节点11处接入一座容量为50 MW的光伏电站,其有功出力可近似为Beta分布(α=β=0.9)。系统内还有两座装机容量为100 MW的完全相同的风电场,假设风速均服从尺度参数为8.09、形状参数为2.17的Weibull分布,风机输出特性可表示为文献[22]中的分段函数。为了比较不同风电接入位置对机组发电调度结果的影响,分别模拟以下3种方案:①风电场位于节点17和节点5;②风电场位于节点17和节点16;③风电场位于节点17和节点26。 考虑风电场及负荷间的相关性,设两座风电场的风速相关系数为0.6,同一区域的负荷之间相关系数均为0.4,而不同地区的负荷则相互独立。其余参数设置如下:置信度cV=cl=0.95;参考隶属度Lr1=Lr2=Lr3=1;惩罚项系数μ1=μ2=1 000;改进ICA的相关参数见附录C表C1。 图1给出了方案1下多目标问题的Pareto最优前沿。由图可知,总碳排放量控制得越少,所需费用也越高。在同等碳排放水平下,维持区域碳排放量平衡(f3越小)会使费用成本直线上升。另外,图中的前沿曲线范围跨度较大,表明可供决策者选择的机组调度方案很多。 图1 目标函数的Pareto前沿Fig.1 Pareto front set of the objective functions 表1比较了3种风电接入方案下的优化结果,包括优化后各机组的有功出力及相应的目标函数值。可以看到,方案1下的f1,f2和f3均最小,优化结果最好,尤其是区域碳排放差异量这一指标明显低于方案2和3。具体各机组出力及区域碳排放量的对比情况如图2、图3所示。由图2可见,碳排放强度越大的机组(P1,P2和P22),计划发电量越小。且有风电接入的区域内,火电机组的出力均有不同程度的减小。越经济的机组,出力减小得越少。图3则能看出,方案1的碳排放总量及差异量均小于方案2和方案3,这是由于区域1的两个火电机组碳排放强度最大,在其同一区域内接入风电场能最大程度上限制该区域的碳排放量,从而更好地维持地区间的碳排放平衡。 表1 不同方案下的模糊优化结果Table 1 Fuzzy optimization results under different cases 为了验证SRSM在概率潮流计算方面的精度和效率,本文以支路10-22的有功功率P10-22为例,在方案1下与MCS和CM得到的概率密度(probability density,PD)曲线进行比较。由图4可知,当不计相关性时,三种方法所得结果基本一致。然而,在考虑输入变量相关性的情况下,CM的图线在顶部存在较大偏差,且左侧尾部区域相较于MCS和SRSM偏小,可能会导致低估系统的运行风险,使得支路过载率超出式(8)的机会约束。而SRSM的结果始终与MCS保持吻合,并且SRSM与CM的计算效率相当(1.046 s和0.671 s),远小于MCS的耗时(682.5 s)。由于实际场景中,集群风电场或光伏电站的关联性往往很强,且系统规模增大导致计算负担更重,相比于传统的MCS和CM,SRSM在计算精度和效率方面的优势将更加明显。 附录D比较了本文改进ICA与其他智能算法(OICA,GA和PSO)对单目标函数f3的迭代收敛曲线,由图中可见,通过前150次迭代,所有算法基本都寻找到了最优解。其中,所提算法收敛速度最快,前10次迭代已基本收敛,寻优能力较改进前有了显著提升,说明新引入的克隆进化算子十分必要。 图2 不同方案下的机组出力Fig.2 Outputs of generators under different cases 图3 不同方案下的区域碳排放量Fig.3 Regional carbon emissions under different cases 图4 不同方法下支路10-22有功的PDFig.4 PDs of line 10-22 under different methods 附录E图E1为江苏省电力调度中心提供的江苏南通市某区域实际电网的拓扑图,系统共有34个节点、48条支路。对节点依次编号,其中将节点1和2(上级变电站的出口母线)视为无穷大电源,在计算中等效为平衡节点。图中A,B,C三点分别为华启风电场、龙海风电场和东凌风电场。根据地理位置将网络划分为3个区域,具体每个区域所包含的节点如附录E表E2所示。 由于实际工程中往往需要根据决策者的需求确定各目标的优先级,通过改变参考隶属度的值可以灵活调节各目标函数的权重。表2给出了不同参考隶属度下实际电网的优化仿真结果,其中碳排放强度为日均碳排放量与24倍负荷功率的比值,其值可以反映一个地区的污染程度。 表2 不同参考隶属度下的模糊优化结果Table 2 Fuzzy optimization results under different reference membership values 由表2可以看出,当f1和f2具有相同的优先级时(Lr1=Lr2=1),改变f3的隶属度对于f1,f2优化结果的影响较小,而f3变化明显(Lr3越大,f3的值越小)。因此,我们可以在保持总发电成本和碳排放量基本不变的前提下,通过增大Lr3,尽量减少区域碳排放的不平衡量。 本文建立了一种基于多目标概率最优潮流的区域电网低碳电力调度模型,与传统的低碳经济调度模型相比,引入区域碳排放差异量作为新的优化目标以平衡不同地区间的污染状况。为应对新能源广泛接入对电网静态安全的挑战,提出了带模糊满意度决策的改进ICA,并结合基于SRSM的概率潮流方法对模型进行求解,主要结论如下。 1)利用SRSM计算系统节点电压和支路潮流的概率分布,能够克服MCS计算规模大及CM在计及输入变量相关性时精度不足的缺陷,保证最优解满足电压和有功出力的机会约束。 2)新能源电站的位置会影响模型的优化结果,将新能源电站接入高负荷密度地区或碳排放强度较大的火电厂附近能够最大程度上减少区域间的碳排放不平衡量,防止局部地区过污染。 3)通过对各目标函数参考隶属度的灵活设置,可以满足调度人员不同的需求,做出最佳的调度决策。 本文成果可用于指导新能源广泛接入地区的火电机组调度,并为新能源场站选址方案的评估提供新的思路。后续将进一步研究考虑碳补集电厂及需求侧资源的调度模型[23],更全面地实现对区域电网碳排放量的综合管理。 感谢东南大学优秀博士学位论文培育基金对本文的资助! 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 参考文献 [1] 卫志农,张思德,孙国强,等.基于碳交易机制的电—气互联综合能源系统低碳经济运行[J].电力系统自动化,2016,40(15):9-16.DOI:10.7500/AEPS20151109004. WEI Zhinong, ZHANG Side, SUN Guoqiang, et al. Carbon trading based low-carbon economic operation for integrated electricity and natural gas energy system[J]. Automation of Electric Power Systems, 2016, 40(15): 9-16. DOI: 10.7500/AEPS20151109004. [2] LIU Z, GUAN D, WEI W, et al. Reduced carbon emission estimates from fossil fuel combustion and cement production in China[J]. Nature, 2015, 524(7565): 335-338. [3] RUI M A, KAI L I, XUAN L I, et al. An economic and low-carbon day-ahead pareto-optimal scheduling for wind farm integrated power systems with demand response[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(3): 393-401. [4] ZENG B, ZHANG J, YANG X, et al. Integrated planning for transition to low-carbon distribution system with renewable energy generation and demand response[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1153-1165. [5] 程耀华,张宁,康重庆,等.考虑需求侧管理的低碳电网规划[J].电力系统自动化,2016,40(23):61-69.DOI:10.7500/AEPS20160411014. CHEN Yaohua, ZHANG Ning, KANG Chongqing, et al. Low carbon transmission expansion planning considering demand side management[J]. Automation of Electric Power Systems, 2016, 40(23): 61-69. DOI: 10.7500/AEPS20160411014. [6] 闫柯柯.基于碳交易的含风电场电力系统低碳经济调度研究[D].秦皇岛:燕山大学,2014. [7] JI Z, KANG C, CHEN Q, et al. Low-carbon power system dispatch incorporating carbon capture power plants[J]. IEEE Transactions on Power Systems, 2013, 28(4): 4615-4623. [8] WANG S, YU D, YU J, et al. Optimal generation scheduling of interconnected wind-coal intensive power systems[J]. IET Generation, Transmission & Distribution, 2016, 10(13): 3276-3287. [9] LE D D, BERIZZI A, BOVO C. A probabilistic security assessment approach to power systems with integrated wind resources[J]. Renewable Energy, 2016, 85: 114-123. [10] 徐青山,黄煜,刘建坤,等.采用混合高斯模型及边缘变换技术的蒙特卡洛随机潮流方法[J].电力系统自动化,2016,40(16):23-30.DOI:10.7500/AEPS20151207007. XU Qingshan, HUANG Yu, LIU Jiankun, et al. Probabilistic load flow method using Monte Carlo simulation based on Gaussian mixture model and marginal transformation[J]. Automation of Electric Power Systems, 2016, 40(16): 23-30. DOI: 10.7500/AEPS20151207007. [11] 刘宇,高山,杨胜春,等.电力系统概率潮流算法综述[J].电力系统自动化,2014,38(23):127-135.DOI:10.7500/AEPS20131014017. LIU Yu, GAO Shan, YANG Shengchun, et al. Review on algorithms for probabilistic load flow in power system[J]. Automation of Electric Power Systems, 2014, 38(23): 127-135. DOI: 10.7500/AEPS20131014017. [12] DELGADO C, DOMINGUEZ-NAVARRO J A. Point estimate method for probabilistic load flow of an unbalanced power distribution system with correlated wind and solar sources[J]. International Journal of Electrical Power & Energy Systems, 2014, 61: 267-278. [13] ZHANG P, LEE S T. Probabilistic load flow computation using the method of combined cumulants and Gram-Charlier expansion[J]. IEEE Transactions on Power Systems, 2004, 19(1): 676-682. [14] 黄煜,徐青山,卞海红,等.基于拉丁超立方采样技术的半不变量法随机潮流计算[J].电力自动化设备,2016,36(11):112-119. HUANG Yu, XU Qingshan, BIAN Haihong, et al. Cumulant method based on Latin hypercube sampling for calculating probabilistic power flow[J]. Electric Power Automation Equipment, 2016, 36(11): 112-119. [15] WANG X, GONG Y, JIANG C. Regional carbon emission management based on probabilistic power flow with correlated stochastic variables[J]. IEEE Transactions on Power Systems, 2015, 30(2): 1094-1103. [16] REN Z, LI W, BILLINTON R, et al. Probabilistic power flow analysis based on the stochastic response surface method[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2307-2315. [17] XIAO Q. Dimension reduction method for probabilistic power flow calculation[J]. IET Generation, Transmission & Distribution, 2015, 9(6): 540-549. [18] ATASHPAZ-GARGARI E, Lucas C. Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition[C]// Proceedings of the IEEE Congress on Evolutionary Computation, September 25-28, 2007, Singapore. [19] 黄煜,徐青山,刘建坤,等.含分布式电源的改进配电网随机潮流计算[J].华南理工大学学报:自然科学版,2017,45(4):44-50. HUANG Yu, XU Qingshan, LIU Jiankun, et al. Improved probabilistic load flow calculation of distribution grids with distributed generation[J]. Journal of South China University of Technology, 2017, 45(4): 44-50. [20] 卫志农,向育鹏,孙国强,等.计及碳排放含有碳捕集电厂电网的多目标动态最优潮流[J].电网技术,2012,36(12):11-17. WEI Zhinong, XIANG Yupeng, SUN Guoqiang, et al. Carbon emission-considered multi-objective dynamic optimal power flow of power system containing carbon-capture plant[J]. Power System Technology, 2012, 36(12): 11-17. [21] CHEN Y L, LIU C C. Interactive fuzzy satisfying method for optimal multi-objective VAR planning in power systems[J]. IEE Proceedings-Generation, Transmission and Distribution, 1994, 141(6): 554-560. [22] MOSHARI A, EBRAHIMI A, FOTUHI-FIRUZABAD M. Short-term impacts of DR programs on reliability of wind integrated power systems considering demand-side uncertainties[J]. IEEE Transactions on Power Systems, 2016, 31(3): 2481-2490. [23] LI Jianming, WEN Jinyu, HAN Xingning. Low-carbon unit commitment with intensive wind power generation and carbon capture power plant[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(1): 63-71.3.2 模糊满意度决策
4 算例分析
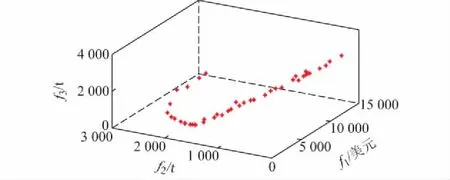
4.1 Matpower 30节点系统

4.2 江苏某区域实际电网

5 结语
