从一道美国数学月刊问题谈起
2018-06-21山东省威海职业学院信息工程系
中学数学教学 2018年3期
山东省威海职业学院信息工程系
姜卫东 (邮编:264210)
设a、b、c、S表示△ABC的三边长和面积.则有[1]

①
这是著名的外森比克(Weisenböck)不等式.
①已有很多种形式的加强,其中最著名的是费-哈不等式

②
最近,罗马尼亚的Nicusor Minculet在《美国数学月刊》2017年第6-7期[2]给出(1)的另一种加强,即如下问题
问题11990:在△ABC中,有
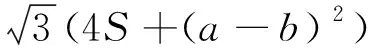
③
注意到文[1,第46至47页]在证明(1)的过程中,已经得到

④
显然④比③更强.
注记由④等价变形,可得
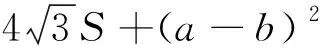
⑤
此即文[4]的主要结论.
现再给出④的一个有趣加强,即下面的
定理1设a、b、c、S表示△ABC的三边长和面积.则
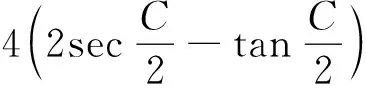
⑥
证明在△ABC中,根据面积公式和余弦定理,有

从而

从而定理1成立.

将⑥等价变形,可得如下的结论:
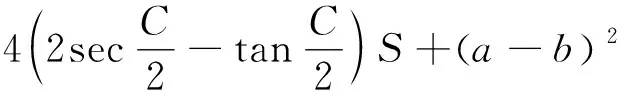
⑦
⑦显然是⑤的一种加强.
联想到安振平老师在《三十个有趣的不等式问题》[3]一文中的问题(29):
设△ABC的三边分别为a、b、c,面积为S,求证:

⑧
受定理1的启发,我们给出⑧的一个加强.
定理2设△ABC的三边分别为a、b、c,面积为S,则:
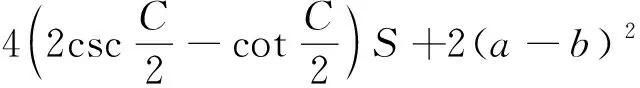
⑨
证明由余弦定理及三角形面积公式,可得
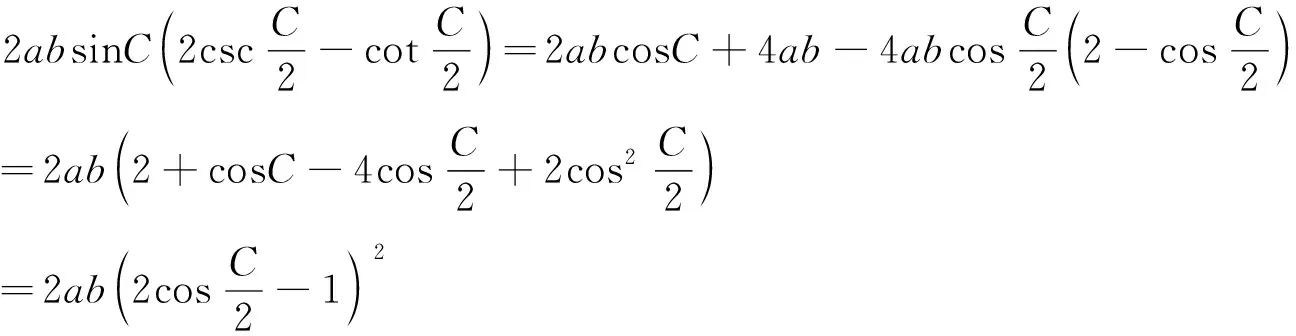
定理2证毕.
推论

⑩
1 O.Bottema等著,单墫译,几何不等式,北京大学出版社,1991
2 American Mathematical Monthly, Vol. 124, No. 6, Jun 2017
3 安振平,三十个有趣的不等式问题[J],中学数学教学参考,2011(11)上旬:58
4 王燕,外森比克不等式的一个有趣加强[J].中学数学教学,2007(4):61
