把握本质规律 提升备考效益——以《坐标系与参数方程》复习为例

福建省闽清教师进修学校

黄如炎 (邮编：350800)

在高考新课程全国卷中，坐标系与参数方程以中档题定位，由于入题容易成为多数考生首选．三角函数(或数列)、立体几何、坐标系与参数方程是平时高考复习中最有成效，也是考生高考时志在必得的三道中档题．2017年高考福建全省理科第(17)题三角函数平均7.05，第(18)题立体几何平均7.45，第(22)题坐标系与参数方程仅平均4.38；文科第(17)题数列平均5.44，第(18)题立体几何平均4.75，第(22)题坐标系与参数方程仅平均3.18[1]．因此教师有必要深入研究教材、考纲、考情、学情，把握坐标系与参数方程的本质与高考考查规律，让学生熟练掌握三种形式方程间的互化，灵活选择适合的坐标系和方程，运用三角函数、解析几何、不等式等知识解决问题，切实提高坐标系与参数方程的复习效益，使坐标系与参数方程成为高考分数的增长点．

1 高考考查规律

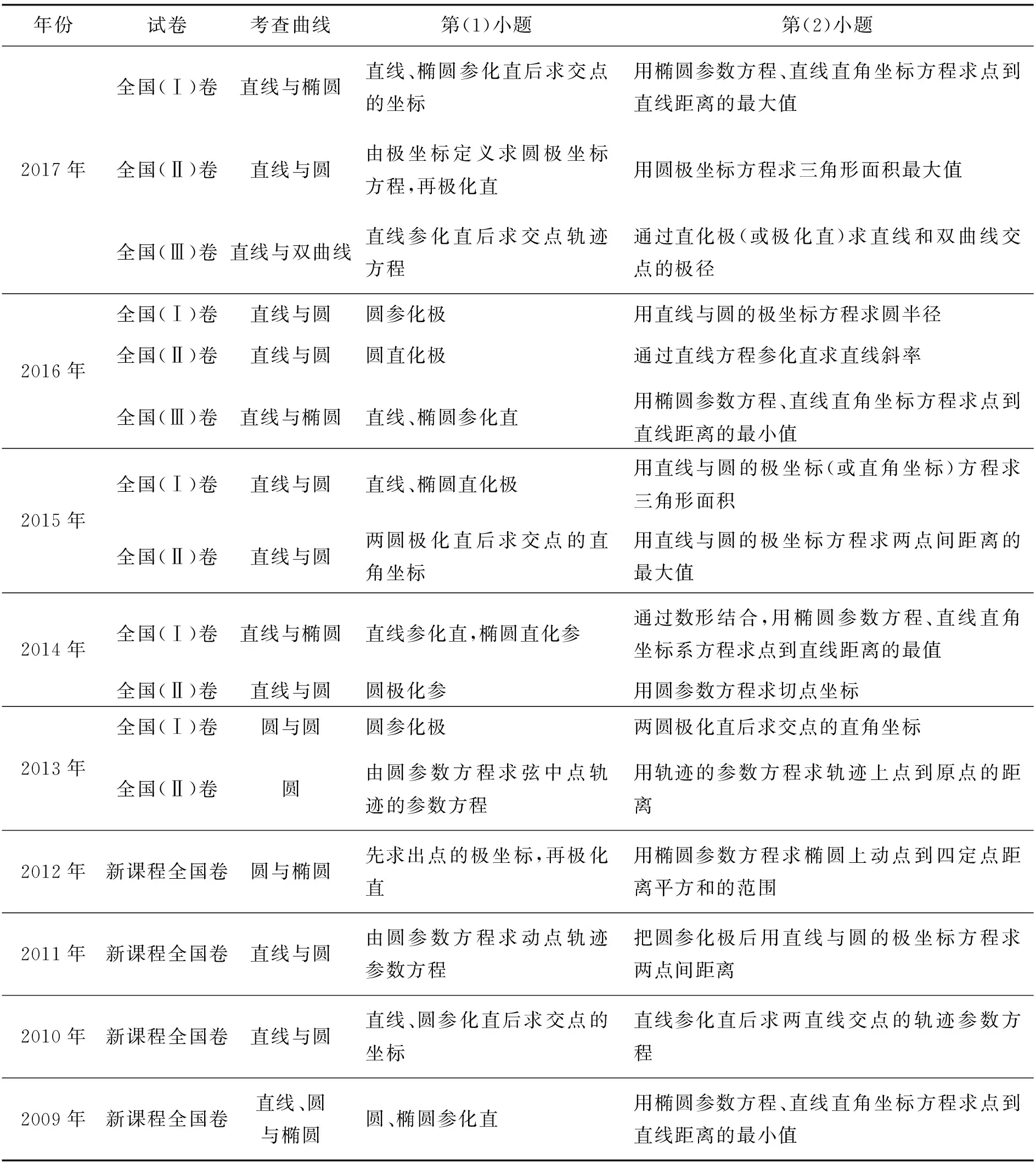
表1 高考全国卷坐标系与参数方程考查情况

从上表发现全国卷坐标系与参数方程的考查颇具规律，考查载体基本上是直线、圆和椭圆．第(1)小题主要考查直角坐标方程、参数方程、极坐标方程间的互化，大多是参数方程和极坐标方程与直角坐标方程间的互化，这种互化只需一次即可完成，但也有考查二次互化即参数方程与极坐标方程间的互化，需先化为直角坐标方程后再化为极坐标方程或参数方程．第(2)小题主要考查选择适合的坐标系或方程，运用三角函数、解析几何、不等式等知识求距离、面积、轨迹和点坐标等问题，而且常用第(1)小题互化结果，即第(1)小题对第(2)小题有提示铺垫的作用．

2 熟练方程互化

3 把握数学本质

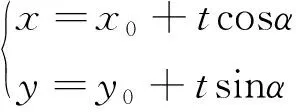
4 强化模拟训练

根据历年坐标系与参数方程的高考考情，教师应把握当年高考走向，精心设计贴近高考又富有新意的例题、习题和考题，做到讲透，练熟．由于选做题安排在最后，要求学生不可依序答题，在完成第一道解答题后就要做坐标系与参数方程，以增加考试的信心和愉悦感，避免因前面难题影响了考试心情甚至无时间完成这道稳操胜券的选做题．

(1)求曲线C的极坐标方程；

(2)求OA·OB的最小值．

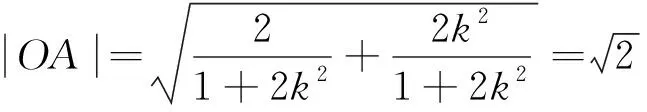
评注本题选择极坐标避免分类讨论且计算量小，体现了极坐标系求解的优越性．

例2在直角坐标系xoy中，曲线C1方程为(x-1)2+y2=1,曲线C2方程为

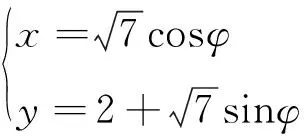
(1)求C2的极坐标方程；

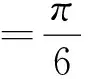
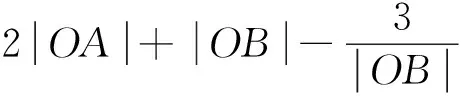
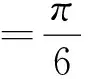
(3)设A(ρA,α)，B(ρB,α)，由于ρA=2cosα,

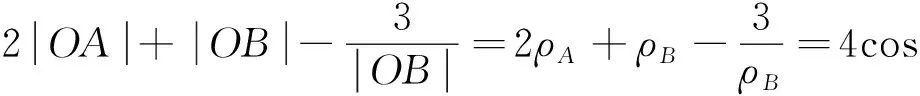
评注本题若选择直角坐标计算量极大，很难求解.

(1)求C1内接矩形周长的最大值；

(2)若直线l与x轴相交于P点，与C1相交于A、B两点，求PA·PB．

解析(1)为减少字母个数，椭圆C1内接矩形顶点的坐标应设为参数坐标形式，设C1内接矩形在第一象限的顶点坐标为(2cosθ,sinθ)，根据椭圆对称性，椭圆内接矩形周长为

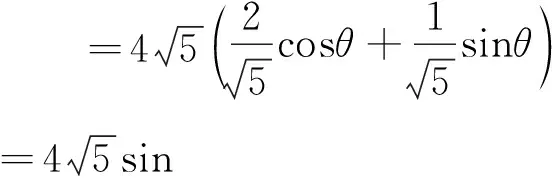
评注本题第(1)小题不再起铺垫提示的作用，对给出的椭圆直角坐标方程和直线极坐标方程需转化为哪种形式的方程考生需要判断.直线参数方程的应用高考尚未考过，应引起师生的注意.

1 福建教育考试院．2017年福建省普通高考学科评价报告[M]．福州：福建教育出版社，2017