采用投影螺旋搜索的改进粒子群算法

高嘉乐,邢清华,李龙跃,范成礼

(空军工程大学防空反导学院,710051,西安)

受鸟群捕食的行为启发,Kenney等于1995年提出了粒子群优化(PSO)算法[1-2],这种算法具有收敛速度快、结构简单等特点,由于它对许多优化问题表现出较高的求解效率而受到国内外广泛的关注[3-5]。但是在求解高维空间的复杂问题时,PSO算法容易早熟且陷入局部最优,在多峰值函数的求解问题中表现更为明显。针对这一问题,很多学者对PSO算法进行优化和改进,主要集中在参数调整和与其他智能算法相结合两个方面。增加随机搜索范围和频率的方式可以避免PSO算法陷入局部最优,采用的方法如模糊逻辑[6]、混沌理论[7]、变化临域粒子辅助更新[8]等。大部分改进算法将基本PSO算法与全局搜索能力较强的智能算法结合,例如多种群方法[9]、人工蜂群(ABC)算法[10]、布谷鸟算法[11]、采用螺旋样式的涡流搜索(VS)算法等。

目前,螺旋搜索(SS)主要应用于反潜搜索路径规划、磁盘阵列搜索等领域,但在连续函数优化方面应用较少。文献[12]提出了一种螺旋粒子群搜索算法,采用了一种螺旋样式的搜索行为以解决PSO早熟问题,这种方法的参数是随机设置的,并且搜索区域尺寸固定,相当于在一个固定尺度搜索空间中的随机搜索,虽然可以避免陷入局部最优,但效率不高。与螺旋搜索样式相似,文献[13]提出一种涡流样式的算法,以当前种群个体为中心在一个衰减半径的区域内进行随机搜索,尽管搜索范围衰减,但这种搜索方式仍然是一种无目的的搜索。文献[14]提出了量子涡流算法,将涡流搜索行为投影到Bloch球面中,投影搜索行为可以有效地避免在搜索后期大范围的无目的的搜索。

螺旋搜索具有很好的全局搜索能力,但是参数多、后期搜索效率低,因此在连续空间的最优化问题中应用较少。针对上述问题,提出了一种基于投影空间的螺旋搜索的粒子更新算法(SSPSO),并应用于粒子群算法中以解决早熟问题。为了增强算法的寻优能力,引入自适应算子选择方法和混沌变异策略。仿真实验表明,本文算法能够以较少的迭代次数收敛,且具有较高的寻优精度和寻优稳定性。

1 基本粒子群算法

粒子群算法的基本概念源于鸟群捕食行为。在粒子群算法中,每一只鸟看作一个粒子,食物是适应度,头鸟则是每一代的全局最优解,所有粒子向着全局最优解进行收敛。每个粒子的速度和位置更新公式为

(1)

(2)

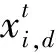
2 基于螺旋搜索的粒子群算法

2.1 螺旋搜索策略

智能算法的搜索方式主要有随机搜索和个体合作两种方法。随机搜索可以分为两种:一种是全局随机搜索,这种方法简单但搜索效率低;另一种是小范围的随机扰动,这种方法是在上一代优秀个体周围进行小范围的随机搜索,搜索效率高且特别适用于求解多峰值问题。个体合作通常用于加快收敛,在优秀个体周围进行搜索容易寻找到更优的个体,但是这种方法也最容易陷入局部最优。受VS算法的启发,结合上述两种搜索策略,本文提出了一种新的螺旋搜索方式。

由于搜索行为是建立在螺旋样式的曲线上,对于螺旋曲线的选择没有固定的要求,本文仅以双曲螺旋线为例

(3)

式中:w是旋转角度,w∈(-∞,0)∪(0,+∞);θ1和θ2是位置扰动参数,θ1、θ2∈(-1,1)。当w趋近于0时,曲线可以近似看作为一条直线;当w趋近于无穷时,曲线则是呈螺旋的样式收敛到(0,0)点。依据上述分析,只要旋转角度不趋近于0,曲线即可呈现螺旋样式。为了便于计算,选取一个整数作为旋转角度的下界,本文设w∈(2π,+∞),使收束曲线呈螺旋形状。

文献[12]中的螺旋搜索方法采用绝对尺度的螺旋曲线在决策空间搜索,搜索后期依然还有很大的搜索范围,虽然绝对尺度的螺旋搜索具有全局搜索的功能,但搜索到更好的个体难度较大。受文献[14]启发,本文提出了一种相对尺度的搜索,即将搜索投影到一个固定的螺旋曲线的空间中,使得搜索尺度随着搜索过程的进行而变化,效率更高。

2.2 基于螺旋搜索的粒子更新

依据个体合作策略选择两个粒子进行合作,一个是当前粒子xi,另一个在种群中随机选择粒子xj。然后在螺旋曲线上随机选择一个点(a1,b1)作为xi的投影点,(a1,b1)称为第一投影点;xj投影到(0,0),(0,0)为第二投影点。假设点(a1,b1)的旋转角度取值w1,在螺旋曲线上生成一个点作为新个体(a2,b2),(a2,b2)的旋转角度w2取值公式为

w2=w1+Lπ

(4)

式中:L是角度控制参数。螺旋搜索示意图如图1所示。图1中2个三角点分别是螺旋线的起点和终点,它们的旋转角度w=2π和w=10π,依据式(3)计算2个点的位置,在图1中标注为三角点。新粒子在螺旋线的投影为(a2,b2)。当L趋近于+∞时,(a2,b2)趋近于(0,0),(a2,b2)在决策空间映射的个体与(0,0)对应的xj相似度增高。当w趋近于+∞时,螺旋线上点的变化趋于0,此时变异差别极小,搜索能力可以忽略不计。

为了避免对个体周围进行过度的局部搜索,定义起始点的旋转角度w1和控制参数L的取值范围,w1∈(2π,10π)和L∈(0,500)。两个参数的下限依据旋转角度w的取值范围定义。w1主要用于确定第一投影点的位置,是螺旋搜索行为的起点。在实验过程中发现,w1对于搜索过程影响不大，因此定义w1是(2π,10π)范围内的随机数。随机生成的目的是为了保证每次搜索行为的随机性,最大限度地避免重复个体的生成。L是螺旋搜索的主要参数,L过大偏重于对第二投影点的周围进行搜索,L过小偏重全局搜索。在实际的参数测试过程中,L的上界较小时对于搜索影响不大,但是L超过500时,算法的搜索效率下降,因此将其上限设为500。

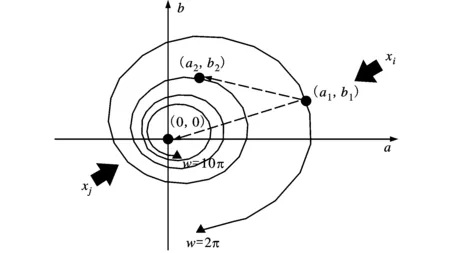
图1 螺旋搜索示意图

螺旋搜索每次只选择粒子的一个维度,即将粒子的一个维度投影到螺旋线(a1,b1)上,得到新生成粒子的两个候选解

(5)

由式(3)可以看出,当w取值趋于π/2的整数倍时,a或b趋近于0。在求解式(5)之后,两个候选解可能超出决策空间的范围,为了避免此类现象发生,选取两个候选解中速度v较小的解作为粒子的下一代解的速度,速度和粒子位置更新如下式

(6)

(7)

从螺旋搜索粒子更新方式可以看出,螺旋搜索的全局寻优策略的优势主要有不同维度变异无相关性和反向搜索能力两方面。对于不同维度变异无相关性来说,每一维度搜索的结果都是不同的,虽然新粒子需要两个父代个体的信息才能产生,但新粒子的速度方向与两个父代个体的连线方向没有直接关系,两个方向呈现正交关系都是可能的。对于反向搜索能力来说,如果新粒子的投影点(a2,b2)与父代个体(a1,b1)在对角象限上,由式(5)可知,新粒子的速度方向为负,即在决策空间上的位置与xj的方向相反,而速度小于2倍的xi与xj之间的距离。

2.3 基于混沌扰动策略的参数设置

完全随机搜索是一种相对低效的但是简单的全局搜索行为,而小概率的扰动可相对高效地提高算法的寻优能力。本文为螺旋搜索行为设置了多个随机参数,这些参数通过扰动促使搜索行为不重复。本文的随机扰动参数主要有4个:第一投影点位置参数w1,曲线扰动参数θ1和θ2,以及控制参数L。

为了提高搜索效率,将混沌思想引入螺旋搜索中,选择经典的Logistic映射[16],计算公式为

zt+1=4zt(1-zt)

(8)

式中:zt∈[0,1]为混沌变量,正整数t为迭代次数。

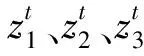
(9)

(10)

(11)

(12)

理论上这种经典的Logistic映射的值域是一个闭区间。为了避免取到参数的边界值,本文添加参数重新生成机制,即如果参数在混沌变异的过程中产生边界值,那么随机取值重新开始混沌变异。

2.4 自适应算子选择

传统PSO个体更新策略具有良好的收敛性,但容易陷入早熟;螺旋搜索具有良好的扰动性,能够提高算法全局寻优能力,但是在收敛速度方面不如传统PSO的更新策略。本文提出一种自适应算子选择策略,在搜索阶段的初期以较大的概率选择传统的PSO粒子更新策略,提高算法的收敛速度,在后期以较大的概率选择螺旋搜索方式,以避免搜索陷入局部最优。定义算子选择概率

(13)

式中:T表示最大迭代次数。在自适应算子选择策略中,首先产生一个随机数,r3∈(0,1)区间,如果随机数小于P,则采用传统PSO更新策略,否则使用螺旋搜索。

2.5 算法描述和分析

下面对算法步骤进行详细描述。

输入:加速因子c1和c2、惯性权重因子c0、种群规模N、最大迭代次数T。

输出:全局最优解pg。

步骤1初始化种群粒子位置和速度;

步骤2计算种群的适应度值,并寻找个体历史最优解pi和全局最优解pg;

步骤3依据2.4节中的自适应算子选择策略,生成随机数r3,如果r3

步骤4使用式(3)和式(4)更新粒子速度与位置,转至步骤7;

步骤5依据2.3节混沌扰动策略生成螺旋搜索参数;

步骤6使用螺旋搜索更新粒子速度与位置;

步骤7更新个体历史最优解pi和全局最优解pg;

步骤8迭代终止条件判断,若满足,转至步骤9,否则转至步骤3;

步骤9输出全局最优解pg,算法结束。

3 实验分析

3.1 测试函数及参数设置

从文献[17]选取常用的高维测试函数检验本文算法性能,测试函数的名称、编号、搜索范围以及理论最优解见表1。其中f1为单峰可分离函数;f2～f5为单峰不可分离函数;f6～f7为多峰不可分离函数;f8～f10为旋转多峰不可分离函数。

将本文提出的SSPSO算法与基本PSO算法、VS算法[13]、量子衍生涡流(QIVS)算法[14]对比。其中,PSO的c0设为0.729,学习因子c1和c2设为0.747,VS和QIVS的参数采用自适应方法生成,无需设置。在仿真中,种群规模N=100,最大迭代次数T=200,测试函数维度n=30。4种算法在10个测试函数中运行30次,将每种算法在每个测试函数上运行结果的平均值、标准差和平均运行时间trun进行比较。仿真实验运行环境为64位Win7操作系统,CPU为Core i5 3.30 GHz,RAM为4 GB。

表1 测试函数描述

3.2 测试和结果分析

4种算法的对比结果见表2,其中黑体的数据为对比结果最优值。从表2中可以看出,本文提出的算法性能良好,10个测试函数中,有8个测试函数得到结果最好。QIVS算法比PSO算法和VS算法的运行结果好,但与SSPSO算法相比只在f5和f8上获得了最好结果,且QIVS算法的平均值与SSPSO算法的结果在同一个数量级。比较PSO算法和VS算法的平均值,PSO算法总体上略优于VS算法。VS算法的不定向变异虽然不容易陷入局部最优,但是其搜索效率是最低的,因此在有限的迭代次数中表现较差。

图2给出了4种算法在迭代过程中的收敛曲线。VS算法整体表现最差,在测试函数f1、f4～f10都是在100次迭代以后才收敛,而且寻优能力相对较弱。PSO算法具有较好的性能,表现出较好的寻优能力,在f1～f3、f5和f10能够以较少的迭代次数收敛。在收敛速度方面,PSO算法弱于QIVS算法和SSPSO算法,在寻优精度方面,PSO算法在f4、f6、f9表现明显不如QIVS算法和SSPSO算法。

(a)f1

(b)f2

(c)f3

(d)f4

(e)f5

(f)f6

(g)f7

(h)f8

(i)f9

(j)f10

表2 4种算法运行结果的平均值和标准差对比

PSO、QIVS、SSPSO 3个算法在f4、f6、f7和f94个测试函数中寻优性能差异明显,其中SSPSO算法能够以较少的迭代次数收敛,且具有明显优于其他3种算法的寻优能力。

表3给出了4种算法在10个测试函数运行时的平均运行时间。PSO算法和VS算法的运行时间在同一个量级,但是PSO算法比VS算法略好。而本文算法和QIVS算法则相对花费较长时间。

表3 4种算法平均运行时间对比

4 结 论

为解决高维空间中复杂多峰函数的优化问题,本文提出了基于投影空间的螺旋搜索粒子更新方式,并引入自适应算子选择和混沌策略,提出了投影螺旋搜索粒子群算法。通过测试函数的实验分析,本文提出的算法在性能上优于传统PSO算法,具有较高的求解精度,能够以较少的迭代次数收敛,适合于求解具有连续空间复杂多峰值特点的工程应用问题。下一步工作主要采用大量的仿真实验和逆向推导的方法优化算法参数设置以及研究不同的投影点选取对于搜索的影响。

参考文献:

[1] KENNEDY J,EBERHART R C. Particle swarm optimization [C]//Proceedings of the IEEE International Conference on Neural Networks. Piscataway,NJ,USA: IEEE,1995: 1942-1948.

[2] EBERHART R,KENNEDY J. A new optimizer using particle swarm theory [C]//Proceedings of the International Symposium on Micro Machine and Human Science. Piscataway,NJ,USA: IEEE,1995: 39-43.

[3] 张卿祎,王兴伟,黄敏. 基于PSO和SA混合优化的智能容错QoS路由机制 [J]. 东北大学学报(自然科学版),2017,38(3): 325-330.

ZHANG Qingyi,WANG Xingwei,HUANG Min. An intelligent fault-tolerant QoS routing mechanism based on PSO and SA hybrid optimization [J]. Journal of Northeastern University(Natural Science),2017,38(3): 325-330.

[5] WITEK H A,CHOU C P,MAZUR G,et al. Automatized parameterization of the density-functional tight-binding method: II Two-center integrals [J]. Journal of the Chinese Chemical Society,2016,63(1): 57-68.

[6] OLIVAS F,VALDEZ F,CASTILLO O,et al. Dynamic parameter adaptation in particle swarm optimization using interval type-2 fuzzy logic [J]. Soft Computing,2016,20(3): 1057-1070.

[7] XU Xiaolong,RONG Hanzhong,TROVATI M,et al. CS-PSO: chaotic particle swarm optimization algorithm for solving combinatorial optimization problems [J]. Soft Computing,2016,2018(22): 1-13.

[8] SUN Wei,LIN Anping,YU Hongshan,et al. All-dimension neighborhood based particle swarm optimization with randomly selected neighbors [J]. Information Sciences,2017,405(9): 141-156.

[9] PORNSING C,SODHI M S,LAMOND B F. Novel self-adaptive particle swarm optimization methods [J]. Soft Computing,2016,20(9): 3579-3593.

[10] LI T H S,LIN C J,KUO Pinghuan,et al. Grasping posture control design for a home service robot using an ABC-based adaptive PSO algorithm [J]. International Journal of Advanced Robotic Systems,2016,13(10): 1-15.

[11] LI Xiangtao,YIN Minghao. A particle swarm inspired cuckoo search algorithm for real parameter optimization [J]. Soft Computing,2016,20(4): 1389-1413.

[12] 滕弘飞,张英男. 螺旋粒子群优化算法的研究简报 [EB/OL]. (2012/4/10)[2017-06-23]. http: //www. docin.com/p-379958059.html.

[14] 李盼池,卢爱平. 量子衍生涡流搜索算法 [J]. 控制与决策,2015,31(6): 990-996.

LI Panchi,LU Aiping. Quantum-inspired vortex search algorithm [J]. Control and Decision,2015,31(6): 990-996.

[15] CLERC M,KENNEDY J. The particle swarm: explosion,stability and convergence in a multi-dimensional complex space [J]. IEEE Transactions on Evolutionary Computation,2002,6(2): 58-73.

[16] LIU Bo,WANG Liang,JIN Yihui,et al. Improved particle swarm optimization combined with chaos [J]. Chaos,Solitons and Fractals,2005,25(5): 1261-1271.

[17] 纪震,廖惠连,吴青华. 粒子群算法及应用 [M]. 北京: 科学出版社,2009: 73-113.