采用弧映射的双层对象分布算法

聂世强,伍卫国,崔金华,薛尚山,刘钊华

(西安交通大学电子与信息工程学院,710049,西安)

对象存储系统由于可扩展和易管理等特点,已经发展成为主流存储系统架构。常见的对象存储系统有Red Hat公司的Ceph存储系统[1]、Facebook的Cassandra存储系统[2]等。对象存储系统中对象是读写的基本单位。客户端调用对象分布算法将对象分布到对象存储设备(OSD)。高效简洁的对象分布算法可以均衡I/O负载、自适应系统的变化、提高数据可靠性[3]。

对象分布算法是对象存储系统的核心组件,针对对象分布问题已有很多研究。为了解决对象分布的均匀性问题，提出一致性哈希算法[4]、层次化一致性哈希算法[5]、双模对象分布算法[6]、Crush算法[7]、分层对象分布算法[8]、随机切片算法[9]等。为了提高存储I/O性能和降低数据热点问题,Xu等提出了EDP算法以保证去重存储系统中均匀读[10];Jouini等提出了适用于文档存储的副本放置算法[11];Gao等提出了根据数据的访问频率分布对象算法[12];Shen等提出了一种应用于BCube网络拓扑结构的提高数据修复速率的对象分布算法[13];Qin等提出了对象分布算法分别针对纠删码存储中降级读和写性能进行优化[14],以上提及的对象分布算法虽然各具特色,但是在对象存储系统的应用中受到诸多约束,不具有普适性。本文利用存储系统批量扩容和删除的特点,设计了弧映射双层对象分布(TMHR)算法。将同一批次的多个存储节点划分为子集群,对象分布过程中,TMHR算法首先采用可扩展的子集群哈希(SHFC)算法选择存放对象的子集群,其次采用随机置换算法在目标子集群内计算存放对象的存储节点。该算法可以在较短时间内计算任意对象的目标OSD节点,保证对象均匀分布,迁移较少的对象以适应OSD节点的动态变化。

1 问题定义

设存储系统以子集群为单位进行扩容和删除,扩容、删除的第i个子集群用Ci表示,其权值用wi表示,wi是子集群Ci内节点容量、性能等特征的量化,根据具体需求赋予权值不同的含义。如以存储容量为量化标准,则1 TB的存储节点和500 GB的存储节点的权值之比为2∶1。Ci拥有的存储节点数为mi。初始时存储系统仅包括子集群C0,所有子集群用子集群集合C表示,所有子集群数用k表示。对象数为y(y≥1),每个对象拥有唯一的识别符,对象数理论上无限,且对象数远远大于节点数。

2 TMHR算法

利用存储系统批量扩容、删除的特性,TMHR算法采用双层映射模式,存储节点按照加入系统的批次被分为多个子集群,相同的子集群内节点性能、容量相似。客户端读写对象时只需要从存储系统获取当前子集群和节点的描述信息,客户端在本地完成对象和其存储节点映射关系的计算,即在子集群间采用SHFC算法以权值为概率选取目标子集群,在目标子集群内采用随机置换算法等概率选择目标节点。

2.1 子集群间SHFC算法

基于动态区间映射算法和随机切片算法两者都将对象存储在以区间为单位的逻辑单元中,两种算法的时间复杂度与区间数均正相关。系统扩容过程中两种算法都会产生大量小区间,虽然随机切片算法提出了4种减小区间碎片化的策略,但是区间数仍然较大,极大地影响了系统I/O性能。为了解决系统扩容造成的区间碎片化问题,SHFC算法将对象和子集群的哈希值映射在半径为R的环形空间,根据子集群的权值将整个环形空间分为相应比例的弧,每个子集群负责存储映射在弧上的对象,并将最大相邻弧合并策略应用于系统的扩容、删除过程。

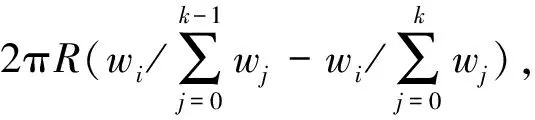
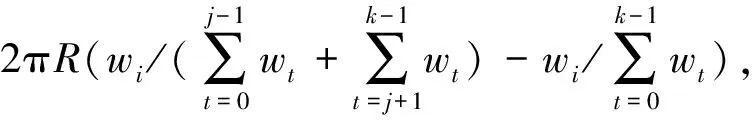
当映射在子集群Ci上的弧序列需要重映射部分弧到子集群Cj时,设需要迁移的弧长为L,设子集群Ci上的弧序列为{a1,a2,…,ae},则最大相邻弧合并策略会尽可能的从子集群Ci的弧序列中找到多个弧au(1≤u≤e)之和的长度接近L。当需要对存在的弧切割时,切割满足如下条件的弧,该弧切割后可以与目标子集群Cj的弧合并,同时该弧是所有满足条件的弧中最长的弧。

存储系统扩容、删除子集群后,SHFC算法不需要重新分割整个环形区间,而是更新发生变化的弧和子集群之间的映射关系,这种策略使重映射的弧长度最短,从而使需要迁移的对象最少。

2.2 子集群内随机置换算法

子集群内的对象分布采用随机置换算法降低计算时间开销。随机置换算法实现了对副本机制的支持,保证同一对象的多个副本均匀分布在OSD节点上。计算对象x的第r个副本存放节点的函数为

f(x,r,m)=(hash(x)+rp)modm

(1)

式中:x是对象的标识符;r是小于m的副本数;p和m都是质数,且满足p>m。m默认等于子集群Ci(0≤i≤k-1)的节点数mi,但是如果子集群Ci的节点数mi并非质数,则m取大于mi的最小质数。式(1)对序列{0,1,…,m-1}进行随机置换生成等概率的新序列,对象x的第t(0≤t≤r-1)个副本存放在新序列的第t位。若新序列的第t位序号大于节点数mi,则顺次选择下一位。存储系统的扩容和删除等都是批量操作,很少或者几乎不会出现单个存储节点加入、删除的情况,单个存储节点故障失效后很快会被替换,子集群内的节点数是维持不变的,因此不需要考虑子集群内的节点变化情况。

3 算法理论分析

3.1 公平性和自适应性分析

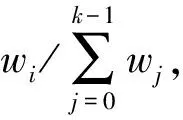
以下证明随机置换算法满足公平性。第2.2节中随机置换算法的核心思想可以用式(1)表示,式(1)可以分解为如下3个运算操作

d=hash(x)modm

(2)

h=rpmodm

(3)

l=(d+h)modm

(4)

式(2)表示以对象x为种子生成随机数,取模映射在{0,1,…,m-1}整数范围内,其值为d。式(3)表示以对象的副本为特征值对序列{0,1,…,m-1}随机置换,文献[15]指出,如果gcd(b,c)=1,bp≡gmodc并且p是解,那么p一定是唯一解,因此可以得出对象x的副本数r和h存在一一映射关系。式(4)表示将置换后的整数序列循环右移了d位得到l。综上可得,式(1)以对象x和副本数r为特征值,将序列{0,1,…,m-1}等概率随机置换生成新序列。若m与子集群Ci的节点数mi相等,则任意节点被选中的概率是1/mi,若m是大于mi的最小质数,重复依次选择下一位,则任意节点被选中的概率是(1/m)·(m/mi)=1/mi,因此随机置换算法满足公平性。

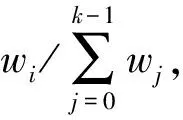
3.2 复杂度分析

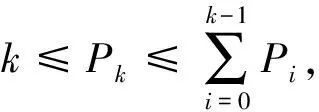
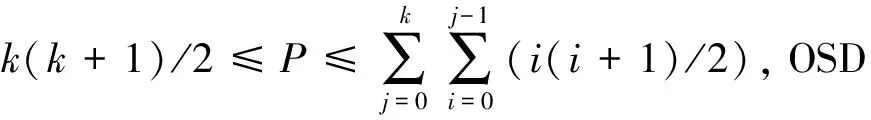
4 实验对比分析

在计算时间、均匀性、公平性和自适应性4个方面比较TMHR算法、一致性哈希算法和随机切片算法,实验的操作系统为ubuntu 14.04 LTS系统,采用python语言实现3种算法。

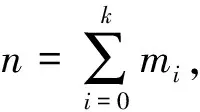
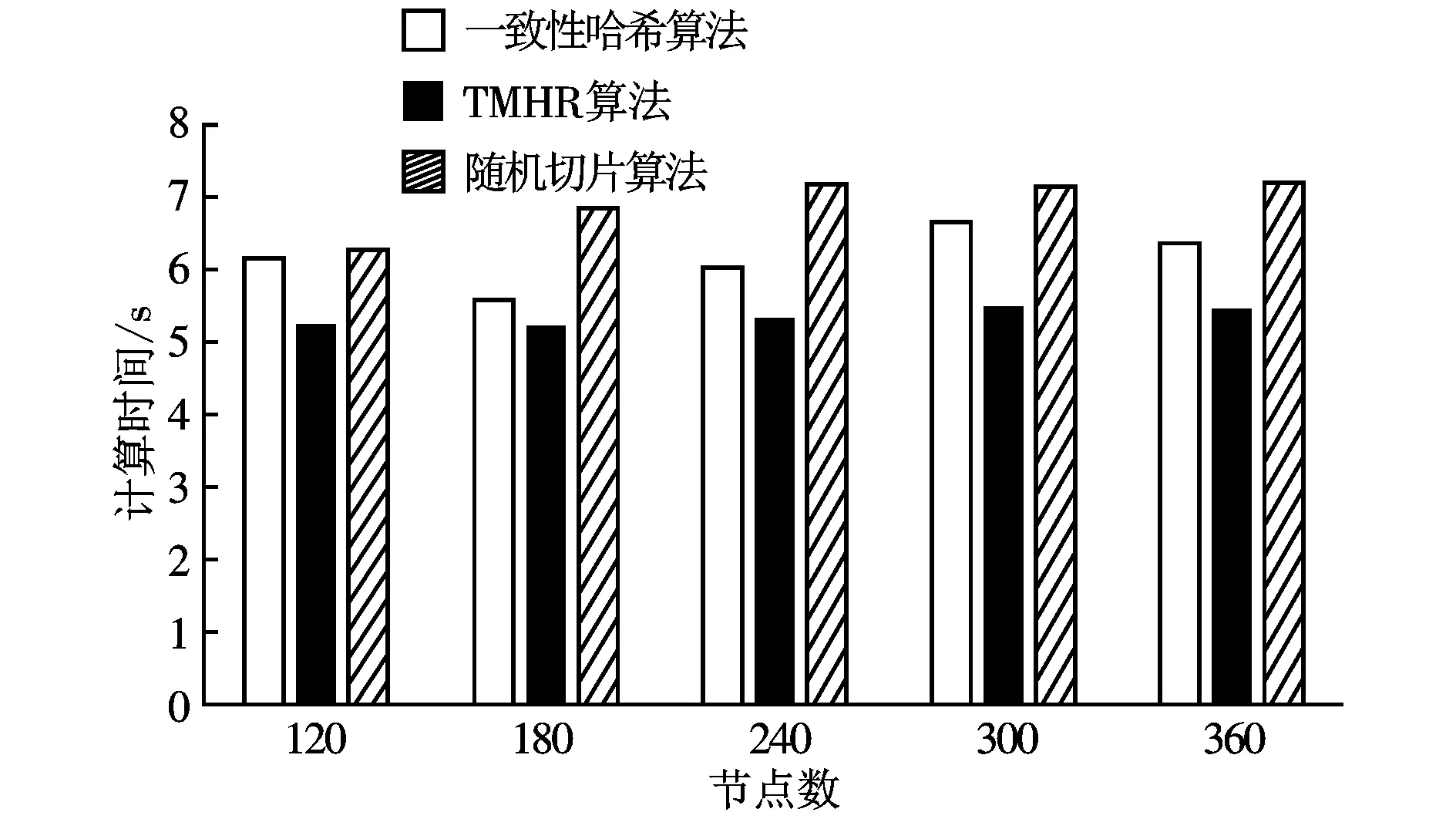
图1 对象分布时间开销的比较

图2给出了将15万个对象分布到由25个节点组成的存储系统后的对象分布情况,25个节点共分为5个子集群,每个子集群包括5个节点,子集群与子集群之间的OSD节点是异构的,5个子集群的权值比为1∶2∶3∶4∶5,从图2可以看出,对象在0～4号子集群内是均匀分布的,子集群间呈现比例分布,也就是说异构环境中对象的分布会随加入OSD节点特性的变化而变化,因此本文算法是完全适应于异构环境的。

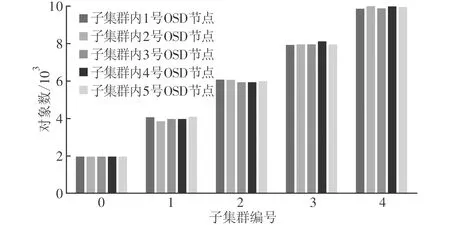
图2 不同权值OSD组成的子集群间对象数比较

图3给出了由120～360个节点组成的存储系统中3种算法分别分布100万个对象的均匀性比较。从图3可以看到,TMHR算法和随机切片算法的方差比一致性哈希算法的方差小,即这两种算法对象分布的更加均匀,有效保证了存储节点的负载均衡。TMHR算法和随机切片算法都可以通过理论证明节点分配的对象数和其权值成正比,并且TMHR算法将对象进行双层映射细粒度分布,比随机切片算法分布更加均匀。一致性哈希算法只是将节点、对象随机分布到环形空间,当数据量较大时对象才能均匀分布,因此其公平性相对较差。

图3 对象分布算法的公平性比较

实验模拟比较一致性哈希算法、TMHR算法在存储系统批量扩容、删除后对象的迁移量,对象迁移量越少表示算法自适应性越好。图4、5给出了180个节点组成的存储系统扩容、删除后每个节点的对象迁移量。存储系统中每5个节点为1个子集群。图4是模拟存储系统的61～120号节点失效后剩余节点的对象迁移量。存储系统中预先已分布了100万个对象,因此理论上可以计算得到在节点删除前每个节点存储的对象数为106/180≈5 555个。在节点删除后,每个节点存储的对象数为106/120≈8 333个,则被删除的节点平均迁移2 778个对象到剩余的节点。从图4可以看出,TMHR算法在1～60号节点和121～180号节点的变化量在2 800左右,实际迁移量和理论值相近,而一致性哈希算法在1～60号节点和121～180号节点的变化量在5 000～6 700左右波动,迁移量较大。此外,61～120号节点的迁移量表示在节点删除前节点的对象数,可以看出在删除前TMHR算法的对象分布相对均匀,每个节点都大致分布了5 500个对象,和理论值5 555大致相等,而一致性哈希算法每个节点分布的对象数波动较大,公平性较差。

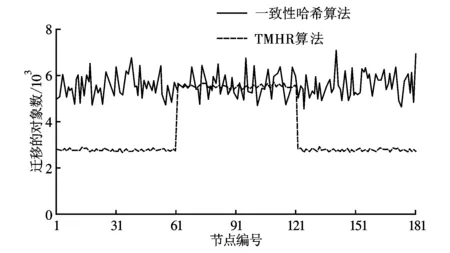
图4 61～120节点失效后的数据迁移量比较

如图5所示是模拟180个节点组成的存储系统加入60个节点后1～180号节点的对象迁移量。系统扩容前每个节点分配的对象数为106/180≈5 555个。在节点增加后,每个节点存储的对象数为106/240≈4 166个,因此扩容后每个节点都要迁移5 555-4 166=1 389个对象到新加入节点。从图5可以看出,TMHR算法中每个节点的对象迁移量和理论值相近,且每个节点迁移量也大致相等,而一致性哈希算法对象迁移量波动较大。

图5 节点增加后的数据迁移量比较

通过模拟实验,从图1～5可以得出如下结论:与一致性哈希算法和随机切片算法相比,TMHR算法在对象分布时间上分别缩短了20%和28%,较快的对象分布有利于客户端快速读写对象,提高系统性能;实验结果表明,TMHR算法可以使对象分布的更加均匀,保证系统负载均衡;当系统扩容、删除后,可以迁移较少的对象以保证对象均匀分布。

5 结 论

大数据时代下,对象分布算法对于对象存储系统的性能影响更加显著。目前,大部分对象分布算法无法在公平性、自适应性、高效性和简洁性取得一定的平衡,很难应用于EB级混合异构存储系统中。本文提出了一种高效简洁的TMHR对象分布算法,算法支持权值和副本机制,在具有较低的时间复杂度的前提下,兼顾了算法的公平性、高效性、简洁性和自适应性。实验模拟结果表明,与一致性哈希算法和随机切片算法相比,TMHR算法在对象分布时间上分别缩短了20%和28%,数据的分布也更加接近于理论情况,对象迁移量方面更加接近理论最优值。异构存储系统中对象分布数量与OSD节点的权值成正比,因此TMHR算法更加适用于异构对象存储系统。

参考文献:

[1] WEIL S A,BRANDT S A,MILLER E L,et al. Ceph: a scalable,high-performance distributed file system [C]//Proceedings of the 7th Symposium on Operating Systems Design and Implementation. New York,USA: ACM,2006: 307-320.

[2] LAKSHMAN A,MALIK P. Cassandra: a decentralized structured storage system [J]. ACM SIGOPS Operating Systems Review,2010,44(2): 35-40.

[3] FACTOR M,METH K,NAOR D,et al. Object storage: the future building block for storage systems [C]//Proceedings of the 2005 IEEE International Symposium on Mass Storage Systems and Technology. Piscataway,NJ,USA: IEEE,2005: 119-123.

[4] KARGER D,LEHMAN E,LEIGHTON T,et al. Consistent hashing and random trees: distributed caching protocols for relieving hot spots on the world wide web [C]//Proceedings of the 29th ACM Symposium on Theory of Computing. New York,USA: ACM,1997: 654-663.

[5] ZHOU J,XIE W,GU Q,et al. Hierarchical consistent hashing for heterogeneous object-based storage [C]//Proceedings of the 14th IEEE International Symposium on Parallel and Distributed Processing with Applications. Piscataway,NJ,USA: IEEE,2016: 1597-1604.

[6] XIE W,ZHOU J,NOBLE J,et al. Two-mode data distribution scheme for heterogeneous storage in data centers [C]//Proceedings of the 2015 IEEE International Conference on Big Data. Piscataway,NJ,USA: IEEE,2015: 327-332.

[7] WEIL S A,BRANDT S A,MILLER E L,et al. CRUSH: controlled,scalable,decentralized placement of replicated data [C]//Proceedings of the 2006 ACM/IEEE Conference on Super-Computing. Piscataway,NJ,USA: IEEE,2006: 31.

[8] 陈涛,肖侬,刘芳. 对象存储系统中一种高效的分层对象布局算法 [J]. 计算机研究与发展,2012,49(4): 887-899.

CHEN Tao,XIAO Nong,LIU Fang. An efficient hierarchical object placement algorithm for object storage systems [J]. Journal of Computer Research and Development,2012,49(4): 887-899.

[9] MIRANDA A,EFFERT S,KANG Y,et al. Random slicing: efficient and scalable data placement for large-scale storage systems [J]. ACM Transactions on Storage,2014,10(3): 1-35.

[10] XU M,ZHU Y,LEE P P C,et al. Even data placement for load balance in reliable distributed deduplication storage systems [C]//Proceedings of the 23th IEEE International Symposium on Quality of Service. Piscataway,NJ,USA: IEEE,2016: 349-358.

[11] JOUINI K. Distorted replicas: intelligent replication schemes to boost I/O throughput in document-stores [C]// Proceedings of the 2017 IEEE/ACS International Conference on Computer Systems and Applications. Piscataway,NJ,USA: IEEE,2017: 25-32.

[12] GAO Y,LI K,JIN Y. Compact,popularity-aware and adaptive hybrid data placement schemes for heterogeneous cloud storage [J]. IEEE Access,2017,5(99): 1306-1318.

[13] SHEN Z,LEE P P C,SHU J,et al. Encoding-aware data placement for efficient degraded reads in XOR-coded storage systems [C]// Proceedings of the 35th IEEE Symposium on Reliable Distributed Systems. Piscataway,NJ,USA: IEEE,2016: 239-248.

[14] QIN Y,AI X,CHEN L,et al. Data placement strategy in data center distributed storage systems [C]// Proceedings of the 2016 IEEE International Conference on Communication Systems. Piscataway,NJ,USA: IEEE,2017: 1-6.

[15] STINSON D R. Combinatorial designs: constructions and analysis [M]. Berlin,Germany: Springer-Verlag,2003: 56-57.