压缩式冷水机组节能优化研究

温海棠,吴爱国,尚羽佳

(天津大学电气自动化与信息工程学院,300072,天津)

作为中央空调系统的核心部分,冷水机组能耗在中央空调系统中比重较大,其中约50%～60%用于制冷机组产生冷量,20%～30%用于冷冻水与冷却水的输配。因此,降低冷水机组能耗是建筑节能工作的重要内容[1]。

目前,很多学者对冷水机组进行了建模与工作点优化计算,以实现机组节能运行,很多先进的建模方法和智能优化算法也已引入到冷水机组优化设计中。文献[2]基于最小二乘法建立了冷水机组在线模型;文献[3]以总能耗为目标函数对冷水机组进行了负荷的优化分配;文献[4]建立了较为精确的冷水机组机理模型,并获得了不同热负荷下系统的优化设定值;文献[5]采用简化性能指标计算冷却水温度的优化设定点，在室外温度大范围变化工况下可以取得4%以上的节能效果;文献[6]建立了制冷机组、水泵和冷却塔等装置的简化数学模型，并在此基础上得到了冷冻水和冷却水的优化设定点，使系统整体能耗减少约0.73%～2.55%;文献[7]采用人工神经网络建立机组模型，并采用粒子群算法与逆神经网络结合的方法优化机组控制参数；文献[8]建立了机组能耗模型,并利用遗传算法进行负荷最优分配以及冷冻水温度优化设定;文献[9]采用一种混合稳态机理模型描述冷水机组各变量的相互关系,通过遗传算法求取系统的优化设定值,在此基础上,采用分散优化算法对优化问题进行求解,从而将求解时间缩短为原来的1%左右[10]。

在保证制冷机组稳定运行的前提下,进一步提高制冷机组运行效率是减小冷水机组整体能耗的有效途径。蒸发器过热度是表征制冷机组运行效率与稳定性的重要参数,设定较低的过热度可以增加蒸发器的有效换热面积,提高制冷机组运行效率,但根据最小稳定过热度(MSS)理论[11],当蒸发器过热度过低时,系统参数会出现严重振荡。目前,大部分研究未充分考虑蒸发器过热度对系统的影响,导致无法保证系统稳定性或者不能充分挖掘制冷机组的节能潜力。

本文通过建立压缩式冷水机组系统稳态机理模型,以机组总能耗最小为优化目标,基于最小稳定过热度理论[11],提出了一种改进过热度约束条件,根据系统负荷取对应负荷下MSS值为过热度约束下限,并采用遗传算法求解系统设定值。实验结果表明,本文提出的优化方法可以有效扩大寻优范围,在保证系统稳定运行的同时进一步提高机组运行效率。

1 冷水机组稳态模型

压缩式冷水机组主要包含3个子系统,即冷冻水系统、制冷机组系统和冷却水系统,如图1所示。

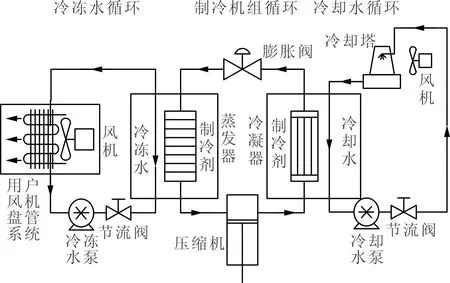
图1 压缩式冷水机组结构示意图

水循环系统的主要动力来自冷冻水泵与冷却水泵,水泵通过消耗电能来维持水介质循环流动,实现与制冷剂的换热。制冷机组是冷水机组的核心部分,主要由压缩机、冷凝器、节流阀及蒸发器4部件组成,其基本工作原理可以通过图2所示的制冷循环压焓(p-h)图表示。

图2中:o点为临界点;ob为饱和液体线,其左侧为过冷区;oc为饱和蒸汽线,其右侧为过热区;ob与oc之间的区域称为两相区。液态制冷剂在蒸发器内不断从冷冻水吸热蒸发为气态,制冷剂温度保持恒定(5—6),气态制冷剂进入过热区继续吸热升温(6—1),1点与6点的温度差即为蒸发器出口的过热度。压缩机消耗电能对气态制冷剂做功,将制冷剂压力由蒸发压力pe升高到冷凝压力pc(1—2);气态制冷剂在冷凝器内向冷却水放热将蒸汽冷却为液态(2—4);液态制冷剂经节流阀节流,压力重新降为蒸发压力(4—5)。

图2 压缩式制冷机组循环压-焓图

为实现冷水机组整体优化,首先需要根据制冷循环建立系统的稳态模型,以便在优化计算过程中确定系统变量。建模过程中出现的制冷剂温度、焓值及密度等物性参数均通过美国国家标准计量局(NIST)开发的REFPROP软件[12]查询。

1.1 蒸发器模型

根据上述对制冷循环过程的分析,可将蒸发器内部按制冷剂状态分为两相区与过热区两部分,如图3所示。

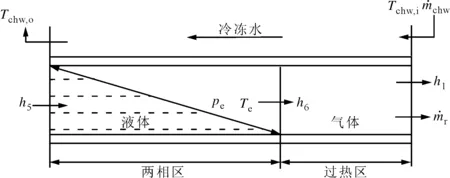
图3 蒸发器相区原理图

本文采用实际工程中应用比较广泛的对数平均温差(LMTD)法计算制冷剂侧与水侧温差,并取LMTD校正因数为1,则蒸发器的稳态传热方程可以表示为

(1)

(2)

其中,Ue,sp与Se,sp分别为蒸发器过热区传热系数与传热面积,Ue,tp为两相区传热系数。由于Ue,sp与Ue,tp可以分别由制冷剂侧与水侧传热系数直接求出,因此式(2)中未知量仅为Se,sp,而Se,sp可以通过过热区内制冷剂侧与水侧能量平衡方程求得

(3)

式中:Tchw,avg为冷冻水平均温度。

过热区与两相区制冷剂侧传热系数由Nusselt’s theory关联式[13]表示

(4)

(5)

冷冻水侧传热系数均由Shah关联式[11]表示

(6)

式中:参数B通过冷却水平均温度计算

B=1 496+22Tw,avg

(7)

蒸发器模型另一个独立方程为制冷剂侧与冷冻水侧能量平衡方程

(8)

1.2 压缩机模型

压缩机质量流量可以表示为[14]

(9)

式中:f、Vcom及ρi分别为压缩机频率、理论输气量和入口制冷剂密度;ηvol为压缩机体积效率,根据下式计算

ηvol=0.98-0.085[(pc/pe)1/1.18-1]

(10)

另一方面,压缩机对制冷剂做功可表示为[14]

Qcom=

(11)

式中:ccom,q,1、ccom,q,2为与压缩机特性有关的常数,通过实验辨识得到。因此,压缩机能量守恒方程为

(12)

1.3 冷凝器模型

根据制冷机组整体能量守恒方程,冷凝器释放热量可以表示为

Qc=Qe+Qcom

(13)

与蒸发器类似,冷凝器内制冷剂侧与冷却水侧的整体热平衡方程可表示为

(14)

式中:Tclw,i为冷却水入口温度;Tclw,o为冷却水出口温度。

冷凝器过热区与两相区是其进行热交换的主要区域,为简化建模及求解过程,冷凝器模型只考虑两相区与过热区,忽略过冷区的影响。因此,根据冷凝器制冷剂侧与冷却水侧的稳态传热方程,可得到冷凝器模型的另一个独立方程

(15)

式中:Sc与Uc分别为冷凝器整体传热面积及换热系数,Uc可表示为过热区与两相区整体传热系数的平均值

(16)

与蒸发器类似,冷凝器过热区传热面积Sc,sp可以通过过热区内制冷剂侧与水侧能量平衡方程求得

(17)

过热区与两相区制冷剂侧传热系数分别由式(4)～式(7)计算。

1.4 过热度模型

在确定系统主要运行参数后,通过蒸发压力pe及蒸发器出口焓h1即可计算蒸发器出口过热度。蒸发器过热度为蒸发器出口温度与饱和温度之差

Tsh=T1(pe,h1)-Te(pe)

(18)

式中:Tsh为过热度;Te为制冷剂蒸发压力下饱和温度;T1为蒸发器出口过热蒸汽温度,为蒸发压力与出口焓值的函数。

式(1)、式(8)、式(12)～式(15)和式(18)构成冷水机组稳态模型,模型输入输出状态如图4所示。在冷水机组控制中,通常将蒸发压力、过热度及冷凝压力作为被控变量,其中过热度可由蒸发压力及蒸发器出口焓值计算,若机组制冷量以及外部输入已知,即可通过机组模型确定系统运行状态。为简化求解过程,本文选择制冷机组内部参数蒸发压力pe、冷凝压力pc及压缩机频率fcom作为优化自由变量。

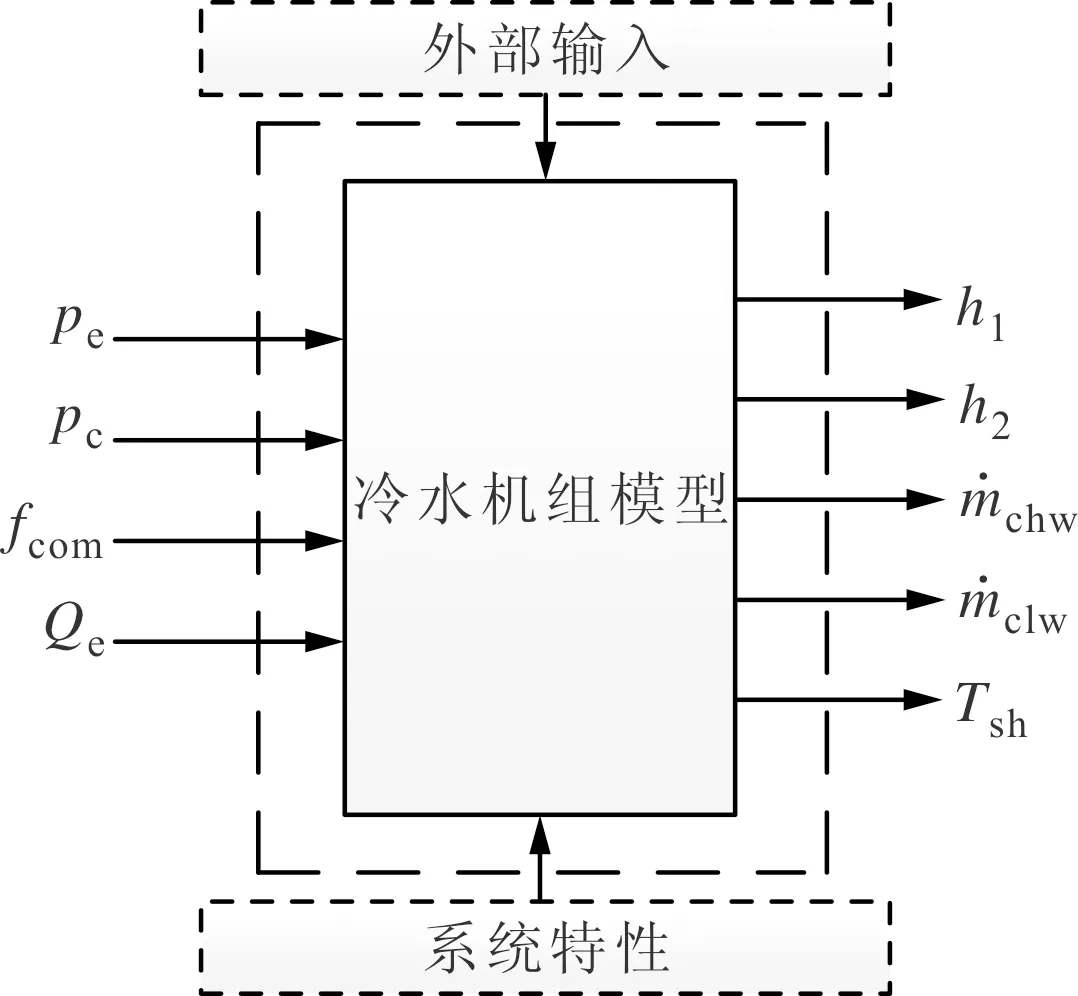
图4 冷水机组模型结构

2 优化问题及求解

冷水机组耗能部件主要是压缩机、冷冻水泵及冷却水泵,降低机组能耗直接体现为3部分功耗之和最小,故优化目标函数可表示为如下形式

minWtotal=Wcom+Wchw+Wclw

(19)

式中:Wcom为冷水机组总功率;Wcom、Wchw及Wclw分别为压缩机、冷冻水泵及冷却水泵功耗。

2.1 压缩机及水泵功耗模型

压缩机功耗为理论功耗与功率系数之比

(20)

其中功率系数为

ηcom,p=ccom,η,1+ccom,η,2(pc/pe)ccom,η,3

(21)

式中:ccom,η,1、ccom,η,2、ccom,η,3为与压缩机特性有关的常数。

冷冻水泵功耗可表示为冷冻水质量流量的多项式形式

(22)

与冷冻水泵类似,冷却水泵功耗与冷却水质量流量的关系如下

(23)

式(22)、式(23)中参数分别由实际数据拟合得到。

2.2 约束条件

冷水机组优化问题中的约束条件可分为自由变量约束、中间变量约束及过热度约束,其中自由变量约束可表示为

(24)

中间变量约束为

(25)

较低的过热度设定值可有效提高制冷机组的运行效率,这导致了过热度优化值通常较低。然而由于MSS的存在,现有优化方法中过热度约束相对比较保守,过热度约束下限通常会高于最大热负荷对应的MSS值。考虑到MSS随热负荷的下降而降低,本文将当前负荷对应的MSS取为过热度约束下限,并随工作条件变化动态改变。这样,更富弹性的过热度约束可以有效增大寻优空间,在进一步挖掘制冷机组节能潜力的同时保证系统的稳定运行。因此,最小化过热度约束如下式所示

TMSS≤Tsh≤20

(26)

式中:TMSS为对应热负荷下MSS值。

2.3 MSS曲线的实验获取

为了在提高系统运行效率的同时保证系统稳定,需要通过实验获得制冷机组在不同制冷量下的MSS值,具体步骤如下。

(1)在每一压缩机频率下给定一个较高的过热度初始设定值,待系统稳定后检测冷冻水流量、供回水温差,计算系统稳态制冷量。

(2)逐渐减小过热度设定值,如图5所示,可以看到,随着过热度设定值的不断降低,过热度在调节过程中的波动幅度会逐渐增大。当设定值减小到某一临界值后,过热度会出现等幅振荡,此临界过热度设定值加0.1 ℃即为该制冷量下系统的MSS值。

(3)逐渐降低压缩机频率(由50 Hz下降到30 Hz),并重复步骤(1)、(2)即可得到不同制冷量下的MSS值。

(4)根据上述实验所得到的数据,利用Matlab工具箱将MSS值与对应制冷量进行多项式拟合,拟合值与实验值对比见图6,拟合公式如下

(27)

图5 制冷量22 kW时MSS的获取过程

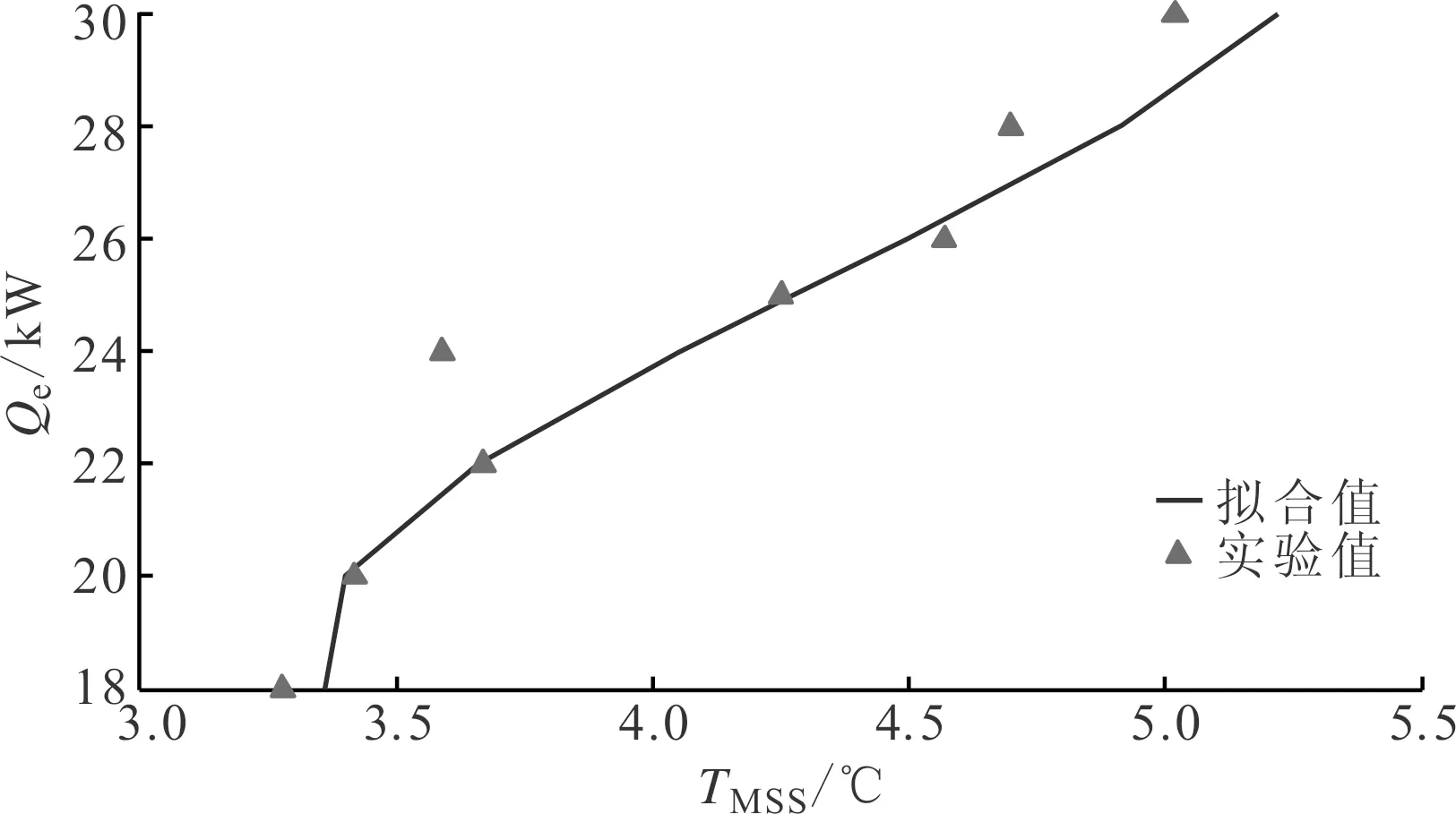
图6 不同制冷量下MSS拟合值及实验值对比

2.4 优化问题的求解

遗传算法具有较强的全局搜索能力和求解动态复杂系统的能力,本文采用遗传算法寻求不同工况下冷水机组的最优设定点,实现系统各部分功耗的最优分配。以最小化机组总功耗Wtotal为优化目标,设计适应度函数以保证优化结果在可行域内[8]。函数式如下

(28)

式中:Ktotal为惩罚函数。采用遗传算法进行优化的具体流程如图7所示。

图7 采用遗传算法进行优化的流程

3 结果与讨论

为验证本文所提出的改进过热度约束对于降低系统能耗的作用,在不同工况条件下设计两组对比实验,一组将过热度约束设为目前常见形式7 ℃～25 ℃,另一组采取本文提出的改进过热度约束,就两种过热度约束实验结果进行对比。

实验装置为图2所示的压缩式冷水机组,通过可编程电加热器模拟实际负荷变化,实验装置详细描述见文献[15]。实验过程中,通过压缩机-蒸发压力、电子膨胀阀-过热度以及冷却水泵-冷凝压力控制回路,将上述3个优化变量保持在优化设定值,以上3个控制回路均采用PI控制算法。冷水机组整体运行效率由所需制冷量与系统整体功耗之比(综合制冷性能系数)表征

(29)

式中:SCOP机组综合制冷性能系数。

3.1 变负荷工况对比实验

在变负荷工况对比实验过程中,环境温度为27.5 ℃,冷却水回水温度23.4 ℃,热负荷由16 kW逐渐上升到30 kW,综合制冷性能系数及过热度对比结果如图8与图9所示。

图8 两种优化方法下综合制冷性能系数对比结果

图9 两种优化方法下过热度对比结果

由图8可见,随着制冷量的升高,系统综合制冷性能系数逐渐降低。采用本文提出的改进过热度优化方法,系统的综合制冷性能系数由3.01逐渐下降到2.43,但在整个制冷量变化过程中均高于现有的优化方法。在热负荷为22 kW时优化幅度最大,约为1.89%;在热负荷为26 kW时最小,仍约为1.05%。

由于较低的过热度可有效降低压缩机运行功耗,因此两种方法的过热度优化值基本达到过热度约束下界。由图9可以看到,现有优化方法过热度优化值均为7 ℃,本文方法的过热度优化值随着制冷量的降低逐渐减小,而且基本沿着MSS线变化(个别工作点略高于对应的MSS)。因此,在热负荷较低的工况下,寻优范围较大,节能效果较为明显;随着热负荷增大,特别是大于26 kW后,两种方法的过热度优化值差距减小,节能效果也更为接近。

图10给出了两种优化方法下蒸发压力、冷凝压力及压缩机频率的优化结果;图11比较了两种优化方法下压缩机及水泵功耗。从图10a、图10b可以看到,在部分负荷下,本文优化方法比现有优化方法得到的冷凝压力优化值更低,蒸发压力值更高。这是由于在最小过热度约束条件下,过热度寻优范围扩大的结果,例如假设系统已经工作在现有优化方法得到的设定点,过热度为7 ℃,若要在保证制冷量不变的条件下进一步降低过热以提升系统能效,则需要增加膨胀阀开度并减小压缩机频率,从而使冷凝压力下降,蒸发压力上升。这样,在压缩机频率及压缩比同时减小的共同作用下,压缩机的功耗得以进一步降低,如图11a所示。

(a)蒸发压力

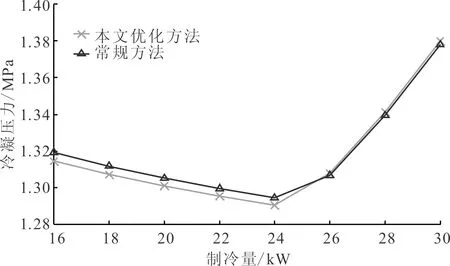
(b)冷凝压力

(c)压缩机频率图10 两种优化方法下系统运行工作点对比

(a)压缩机功耗

由于主要通过优化制冷机组内部运行参数提升冷水机组运行效率,因此并不需要牺牲水泵功耗。由图11b也可以看到,在不同热负荷工况下,两种优化方法下水泵功耗较为接近,本文优化方法下水泵功耗甚至更低。综上所述,本文优化方法在合理分配制冷机组及水循环系统功耗基础上,进一步挖掘了制冷机组的节能潜力,提升了冷水机组的整体运行效率。

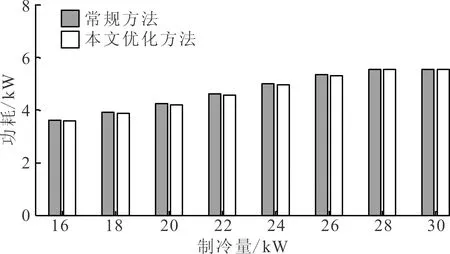
(b)水泵功耗图11 两种方法压缩机及水泵功耗的对比

3.2 负荷与环境温度变化工况对比实验

为进一步检验本文优化方法的实际节能效果,在热负荷与环境温度均变化的工况下设计对比实验。这里以天津某建筑实际数据为基础,用电加热器模拟实际热负荷。图12为该建筑一天24 h热负荷的变化情况,图13为天津夏季环境温度变化的典型情况,可以看到,由于墙体隔离作用,实际热负荷变化比环境温度滞后约1 h,这是因为但是两者的变化趋势基本一致。这是因为当热负荷与环境温度较高时,压缩机与水泵将更多的热量由冷冻水输送到高温冷却水需要做更多的功,在增加制冷成本的同时导致节能空间减小。

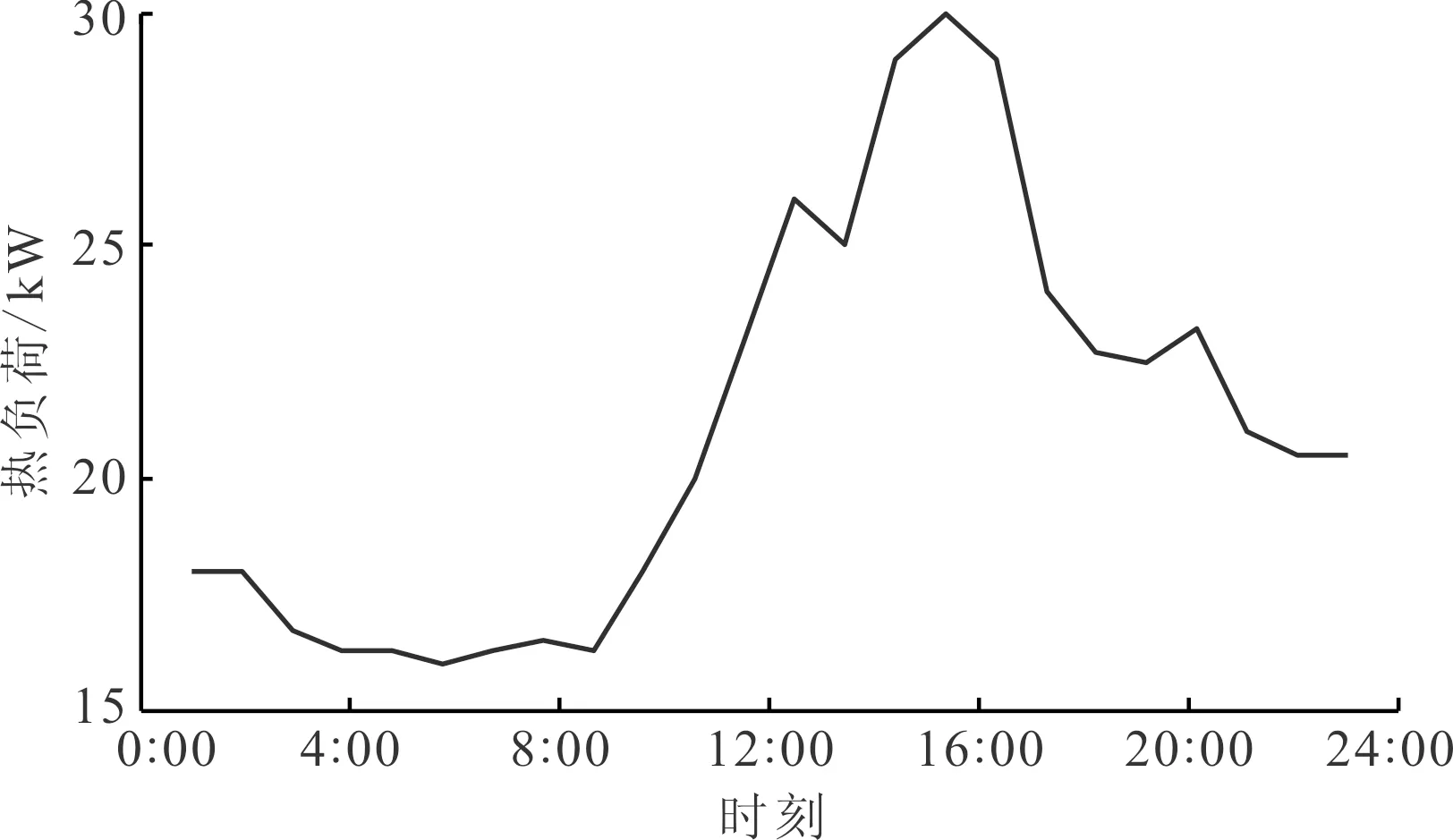
图12 天津某建筑热负荷曲线

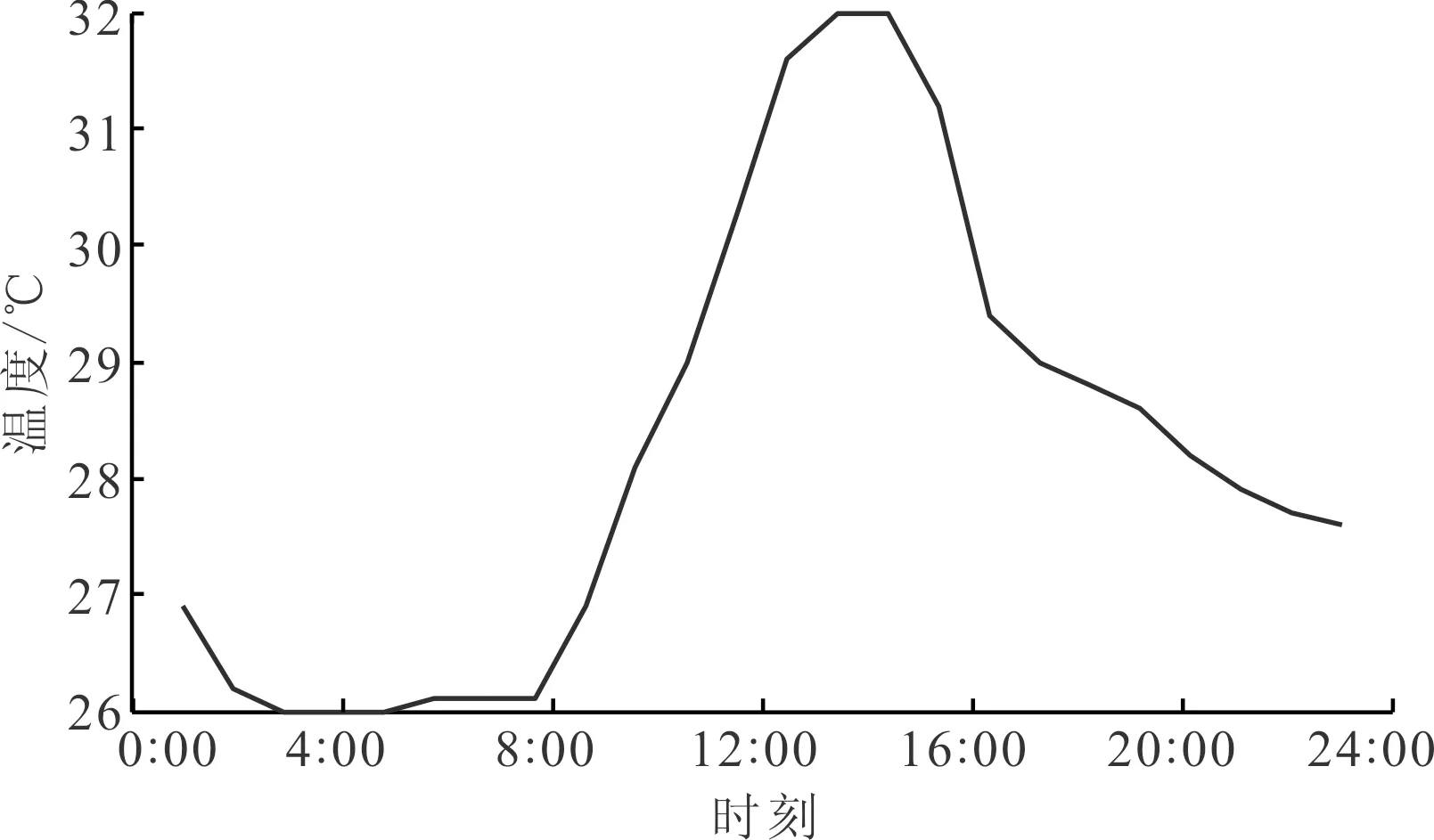
图13 天津夏季环境温度典型曲线

图14给出了两种优化方法在一天内综合制冷性能系数的对比结果,可以看到,在所有时间点,本文方法的系统运行效率均高于现有优化方法。在热负荷及环境温度相对较高的14:00～16:00时间段,两种方法的综合制冷性能系数较低且非常接近,而在制冷成本较低的其他时段,综合制冷性能系数相对较高,且本文方法对综合制冷性能系数的提升较为明显。

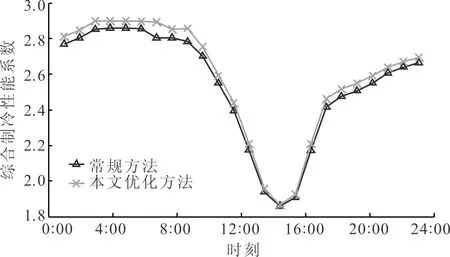
图14 综合制冷性能系数对比结果

最后,为进一步说明在不同时间点改进过热度约束所带来的节能效果,图15给出了工作时段8:00～20:00中,本文方法的系统整体功耗及节能效果。从中可以看到,与现有优化方法相比,本文优化方法在所有时间点均进一步降低了冷水机组整体功耗。在制冷成本较高的14:00～16:00时平均节能约0.85%,而在上午9:00可进一步减少系统整体功耗达3.2%,在工作时段的平均节能量为1.92%。

图15 工作时段中本文方法的系统功耗及节能效果

4 结 论

本文根据热力学定律建立了压缩式冷水机组稳态机理模型。在考虑到蒸发器过热度对系统运行效率及稳定性影响的基础上,提出了改进过热度优化方法。与现有优化方法进行了一系列对比实验表明:①改进过热度约束可以有效扩大寻优范围,从而比现有优化方法进一步降低了系统整体功耗,引入MSS值为冷水机组的稳定运行提供了理论保证;②由于系统MSS值随着负荷的降低而降低,因此本文方法在部分负荷下可取得更为明显的节能效果;③在夏季典型工况下的工作时段,比现有优化方法实现平均节能1.92%。本文的研究结果对节约压缩式冷水机组运行成本、增强运行稳定性具有一定的实际意义。

参考文献:

[1] JIANG Y. Chinese building energy consumption situation and energy efficiency strategy [J]. New Architecture,2008(2): 4-7.

[2] 陈丹丹,晋欣桥,杜志敏,等. 多台冷水机组联合运行空调系统的负荷优化分配 [J]. 上海交通大学学报,2007,41(6): 974-977.

CHEN Dandan,JIN Xinqiao,DU Zhimin,et al. The optimal loading strategy of multiple chillers in HVAC systems [J]. Journal of Shanghai Jiaotong University,2007,41(6): 974-977.

[3] 闫秀英,孟庆龙,任庆昌,等. 联合运行冷水机组负荷优化分配及仿真研究 [J]. 暖通空调,2007,37(11): 18-21.

YAN Xiuying,MENG Qinglong,REN Qingchang,et al. Optimal load sharing strategy for multiple-chiller systems and its simulation [J]. Journal of HV&AC,2007,37(11): 18-21.

[4] NAVARRO-ESBRIJ J,GINESTAR D,BELMAN J M,et al. Application of a lumped model for predicting energy performance of a variable-speed vapour compression system [J]. Applied Thermal Engineering,2010,30(4): 286-294.

[5] LIU C W,CHUAH Y K. A study on an optimal approach temperature control strategy of condensing water temperature for energy saving [J]. International Journal of Refrigeration,2011,34(3):816-823.

[6] MA Z J,WANG S W. Supervisory and optimal control of central chiller plants using simplified adaptive models and genetic algorithm [J]. Applied Energy,2011,88(1):198-211.

[7] 王亚昆,吴爱国,董娜. 吸收式制冷机组逆神经网络设定优化 [J]. 西安交通大学学报,2018,52(1): 123-142.

WANG Yakun,WU Aiguo,DONG Na. A set point optimization method for absorption chiller based on inverse neural network [J]. Journal of Xi’an Jiaotong University,2018,52(1): 123-142.

[8] 闫唯嘉,任庆昌,闫秀英. 基于遗传算法的冷水机组负荷分配与出水温度的优化 [J]. 制冷与空调(北京),2011,11(2): 37-40.

YAN Weijia,REN Qingchang,YAN Xiuying. Load distribution of chillers and the optimum of its outlet water based on genetic algorithm [J]. Refrigeration and Air-Conditioning,2011,11(2): 37-40.

[9] ZHAO L,CAI W J,DING X D,et al. Model-based optimization for vapor compression refrigeration cycle [J]. Energy,2013,55(55): 392-402.

[10] ZHAO L,CAI W J,DING X D,et al. Decentralized optimization for vapor compression refrigeration cycle [J]. Applied Thermal Engineering,2013,51(1/2): 753-763.

[11] FALLAHSOHI H,CHANGENET C,PLACE S,et al. Predictive functional control of an expansion valve for minimizing the superheat of an evaporator [J]. International Journal of Refrigeration,2010,33(2): 409-418.

[12] LEMMON E W,HUBER M L,MCLINDEN M O. NIST standard reference database 23: reference fluid thermodynamic and transport properties (REFPROP): version 8.0 [EB/OL]. (2007-11-02) . http://users.ugent.be/～mvbelleg/literatuur%20SCHX%20-%20Stijn%20Daelman/ORCNext/Supercritical/Software %20EES/REFPROP8.pdf.

[13] SHANG Y J,WU A G,FANG X,et al. Dynamic simulation of electronic expansion valve controlled refrigeration system under different heat transfer conditions [J]. International Journal of Refrigeration,2016,72: 41-52.

[14] DING X D,JIA L,CAI W J,et al. A hybrid modeling for the real-time control and optimization of compressors [C]// 2009 4th IEEE Conference on Industrial Electronics and Applications. Piscataway,NJ,USA: IEEE,2009: 3256-3261.

[15] SHANG Y J,WU A G,FANG X. A study on the modeling of the minimal stable superheat for a variable speed refrigeration system [J]. International Journal of Refrigeration,2015,59: 182-189.