油套管回收车辆路径问题及基于清除小生境差分演化求解算法研究

潘雯雯，郭海湘,2,3, 杜天松, 刘 晓, 王德运

(1.中国地质大学经济管理学院，湖北 武汉 430074；2. 国土资源部国土资源战略研究重点实验室，湖北 武汉 430074；3. 中国地质大学中国矿产资源战略与政策研究中心，湖北 武汉 430074)

1 引言

车辆路径问题(Vehicle Routing Problem，VRP)是由Dantzig和Ramser[1]于1959年首先提出来的，很快引起了相关学者的高度重视。VRP[2-3]作为供应链与物流管理科学研究的主要内容之一，是短期决策，具有很强的时效性。就是说，若能在有效时间内确定最优的车辆路径方案，能有效地节约成本或增加收益；否则，可能会造成一定的损失。随着物流业的快速发展，VRP已广泛应用于危险品运输、应急物流、速递、电商配送[4-6]等方面。按照车辆服务的方向可将VRP分为正向物流VRP和逆向物流VRP。这其中，逆向物流VRP是VRP研究的一个重要分支。逆向物流VRP主要应用于废弃物回收、资源再回收[7-8]等方面。很多学者也研究了同时送取VRP[9-10]，其中送是正向物流，取是逆向物流。

随着社会的发展，国内石油消费量逐年增加：由2011年消费石油4.64亿吨增至2016年消费石油5.76亿吨；而国际石油价格逐年降低：由2011年为111.26美元/桶降至2016年55.21美元/桶，这导致石油利润空间在不断缩小。因此，油田资源的有效利用、成本的合理节约成为油田工作重心之一，油田运输规划将对油田的生产效益产生一定的影响。油田注水系统和输送原油的管道网络布局成为油田运输规划研究的主要内容之一[11-12]。而陆上油田开采过程中所需物资和油田的部分产品均由车辆完成运输，所以VRP仍是陆上油田运输最重要的内容：达列雄[13]针对油田灾害事故救援物资需求量大、待救援点多等特点，研究了油田灾害事故应急资源调度问题，在确保救援效果的情况下尽可能降低成本；王鑫[14]对胜利油田物资配送问题的研究不仅提高了油田物流效率，而且有效地降低了油田物流成本。戴永寿等[15]针对采油厂特种车辆数目少、作业任务多、调度复杂且人工安排结果差的问题，提出了一种基于改进k-means和遗传算法的多目标分阶段求解的特种车优化调度方法，可在现有车辆不足的情况下尽可能多地完成上报的需求不同的任务，并减少车辆的行驶距离。海上油田开采过程中，原油调度、钻井平台所需的物资配送、人员输送等都可能采用船只，所以车辆(船只/船舶)运输问题也是海上油田运输的主要部分。Hennig等[16]基于将原油从生产基地运送到炼油厂的现实问题，研究带时间窗的海上油田车辆路径问题。Cuesta等[17]根据海上油气运输背景提出同时取送的多车型(船舶)车辆路径问题。Carotenuto等[18]研究周期性燃油配送车辆路径问题。

国内研究油田VRP的文献较少，而研究油田逆向物流VRP的相关文献更少。但是煤矿等相关行业VRP的研究对油田VRP的研究具有一定的借鉴意义，杨娟等[19]在在考虑客户服务优先级、车辆装载率、危险物资不能混装等约束条件下研究煤矿企业的物资配送问题。虽然目前有少数学者研究油田逆向物流VRP，但是均未考虑回收价值这一决定性因素。实际上，在油田逆向物流VRP决策中，决策者会考虑回收物资所花费的成本是否低于回收物资本身的价值，即待回收物资是否值得花费人力、物力、财力回收，若没有回收价值，理性情况下就不会回收。在油田油套管回收的决策中，就有此类问题存在。例如：中国石油化工集团公司华北分公司鄂尔多斯盆地南部(简称“鄂南”)的物资装备供应中心每次配送的油管和套管(简称“油套管”)比钻井的需求量多，多数情况这些油套管是无法完全使用完，并且在钻井工作中油套管用量较大，费用较高。若将剩余的油套管随意放置会导致资源的极大浪费、增加成本，但不合理的回收决策往往会导致回收所耗资源远超过待回收物资本身，失去了回收油套管的意义。因此如何在确保油套管的回收意义的基础上得到合理的油套管回收方案是该企业面临的一个现实性问题。

现要对鄂南油区内各油井多余的油套管进行回收。鄂南油区现有红河油田、泾河油田、渭北油田和洛河油田四个油田，石油资源探明率仅2.36%，勘探潜力巨大，是中石化华北分公司的重要石油开采区[20]。在当前生产中，有94口钻井有剩余油套管，现要求回收这些剩余油套管，并确保回收的意义。确保油套管的回收意义是本文的重点和难点。因此，本文将油套管回收价值这一重要影响因素量化到油套管回收VRP模型中，并设计基于清除小生镜技术的差分演化算法(简称jDE_Niche算法)求解数学模型。从而得到合理的油套管回收方案。

2 数学模型

油管和套管是油田开采作业中的关键物资。为了避免由于物资不足造成生产中断，物资供应部门会配送比计划需求量更多的油套管。在少数油井，多配送的油套管会被使用；但其他油井会有剩余的油套管。若将剩余的油套管长期放置于施工场所不使用，会导致这些油套管无法使用，造成资源浪费，所以，油田考虑回收剩余的油套管。但是，油田覆盖范围广，油井位置分散，造成油套管回收成本较高。若油套管的回收成本高于油套管本身的价值，那么就失去了油套管回收的意义和价值。因此，本文建立了考虑油套管回收价值的VRP模型。

为了更清晰地描述本文油套管回收问题，现做以下说明：

(1)每口油井只被一个车辆服务；

(2)无车辆数量限制。

N表示节点的集合，其中包括1个油套管回收站(用No表示)和94口油井；K表示运输车辆的集合；c表示油套管的运输单价；z表示车辆空载部分的惩罚成本；dij表示任意节点i到节点j的行车距离；Vij表示车辆在节点i和j之间时的装载量；pi表示在节点i的油套管回收量；Qk表示第k种车型的最大装载量；ri表示节点i被回收油套管的折旧率；wi表示节点i被回收油套管的购买费用。

决策变量：

xijk=

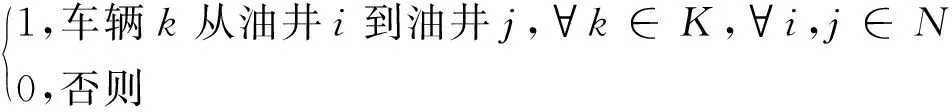
数学模型：

(1)

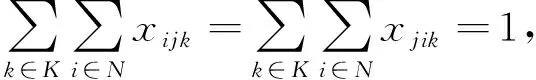
(2)

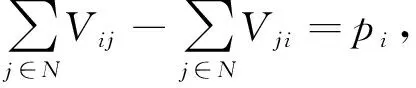
(3)

(4)

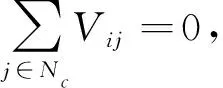
(5)

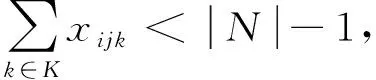
(6)

xijk∈{0,1}，∀i,j∈N,∀k∈K

(7)

Vij≥0，∀i,j∈N

(8)

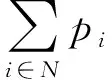
上述数学模型只是考虑了车辆非满载部分的惩罚成本的VRP模型，并没有考虑油套管回收价值的约束。下面描述油套管回收价值约束，如式(9)。

(9)

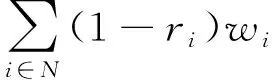
3 算法设计

VRP是NP难的问题，当问题规模扩大时，精确算法的求解时间会随指数增长，这将直接影响决策的时效性。智能算法是众多学者们解决NP难问题的常用方法，进化算法是其中有效的一类。其中，差分演化算法(Differential Evolution Algorithm，DE)是一种对于非线性问题进行全局优化的算法，具有参数少、容错性好、易于编码等优点[21]。而且，在不改变算法结构的情况下，对算法的参数进行调整可以增强算法的全局搜索能力并加快其收敛速度：Ali和Törn[22]提出了缩放因子自适应调整的DE，Brest和Greiner[23]在Ali和Törn[22]的基础上提出了缩放因子和交叉因子自适应调整的DE——jDE算法。jDE能有效地提高算法的优化能力，所以本文改进jDE算法。

变异操作是算法进化操作过程中产生新个体的主要方式，DE的基本变异策略包括DE/rand/1和DE/best/1，其中DE/rand/1是随机的变异过程，保证了变异结果的多样性，但变异过程没有方向性；DE/best/1是在种群中最优个体的基础上变异，但变异结果缺乏多样性。所以，本文考虑将清除小生镜技术融入变异操作过程中，既遵循“优胜劣汰”的原则，也有效地确保种群变异的多样性；设计了jDE_Niche算法。种群初始化和进化操作是算法的主要内容，其中种群初始化包括染色体的编码和解码，进化操作包括变异、交叉和选择操作。

3.1 种群初始化

本文编码采用客户排列和隐型车辆模式，即染色体编码只体现客户的服务顺序，不直接显示车辆信息，根据车辆装载能力和客户需求按客户服务顺序分配车辆；并设计两种车辆分配方式。其中第一种车辆分配方式：首先预设车辆装载率阈值；一条路径可由多种车型服务，每种车型根据其装载能力不同服务不同数量的客户点，然后判断服务该路径的每种车型的装载率，(a)若两种(或两种以上)车型的装载率达到阈值，则优先选择载重量较大的车型；(b)若只有一种车型的装载率达到阈值，则选择此车型；(c)若所有车型的装载量均未达到阈值，则选择装载率最高的车型；在确定第一条路径服务车型后，仍然使用该原则选择第二条路径服务车型，依此类推至所有客户的需求被满足。第二种车辆分配方式：遍历能满足所有客户需求的车辆组合，优先选择车辆数量少、平均装载率高的组合完成服务。本文在实验部分，基于相同的算法设置，比较两种不同的车辆分配方式对算法求解的影响。

图1是一个随机生成的染色体，按基因位数值进行排序得到客户服务顺序，其中整数表示客户编号，括号内的实数表示客户需求。现有装载能力为4、10、15的三种车型，采用两种车辆分配方式的示意见表1和表2，其中被选择的车型已加粗。

3.2 进化操作

DE对染色体的主要操作依次是变异操作、交叉操作和选择操作，本文将清除小生镜技术融于变异操作过程。

小生镜机制的思想是“物以类聚，人以群分”；首先将种群分为多个类(小生镜)；然后在种群内、种群间进行进化操作，产生新种群；进化过程中同类个体间存在竞争，不同种群间有信息交换。清除小生镜技术是选取每个小生镜中最优个体组成当前种群的子种群——最优个体群；其中既有原始种群中较优的个体，也不失种群的多样性。

图1 算法染色体编码示意图

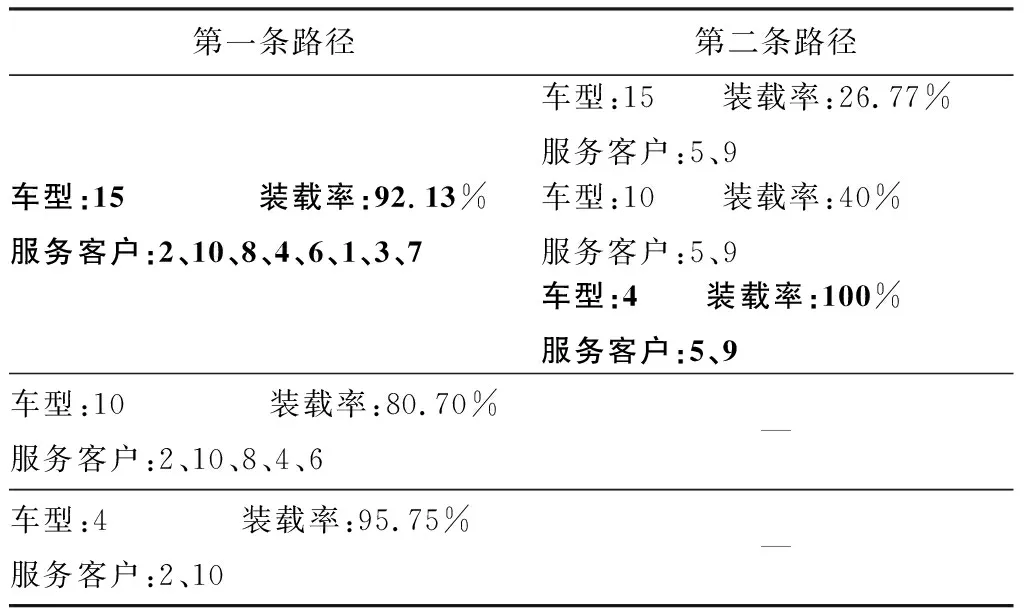
第一条路径第二条路径车型:15 装载率:92.13%服务客户:2、10、8、4、6、1、3、7车型:15 装载率:26.77%服务客户:5、9车型:10 装载率:40%服务客户:5、9车型:4 装载率:100%服务客户:5、9车型:10 装载率:80.70%服务客户:2、10、8、4、6—车型:4 装载率:95.75%服务客户:2、10—

注：车辆装载率阈值为90%，表中第二条路径的车型选择基于第一条路径车型分配结果。

本文在变异操作前，选出优秀个体群——winner集，流程如表3所示。为了便于操作，小生镜容量取值为1；小生镜半径的取值为(0,1)。

DE的差分就是体现在变异操作上，本文采用基于清除小生镜技术的DE/rand/1模式进行变异，如式(10)所示：

Vk,G=Xw,G+F(Xr1,G-Xr2,G)

(10)

其中Xw,G是从winner集中随机选取的个体，Xr1,G、Xr2,G是当前种群中随机挑选出的个体且k≠r1，k≠r2，r1≠r2，Vk,G是变异后的个体，缩放因子F是自适应调整参数。变异操作见图2。

表2 第二种车辆分配方式示意表

注：括号内表示被服务的客户编号。

表3 清除小生镜技术流程

本文交叉操作采用二项式交叉模式(见图3)，其中交叉概率Cr为自适应参数，且jrand=10。选择操作采用贪婪选择策略，如图4。

4 算例分析

4.1 背景分析

中国石油化工集团公司华北分公司鄂南油区现有一个油套管回收处理中心，要回收鄂南油区94口油井共剩余173.77吨油套管，其中每根油管、套管的长度都在8～13米的范围内，每米油管、套管的平均重量分别为10千克和48千克，所以每根油管、套管的重量分别在80到130千克和384到624千克，每口油井剩余油套管的量如表4。

图2 染色体变异操作示意图

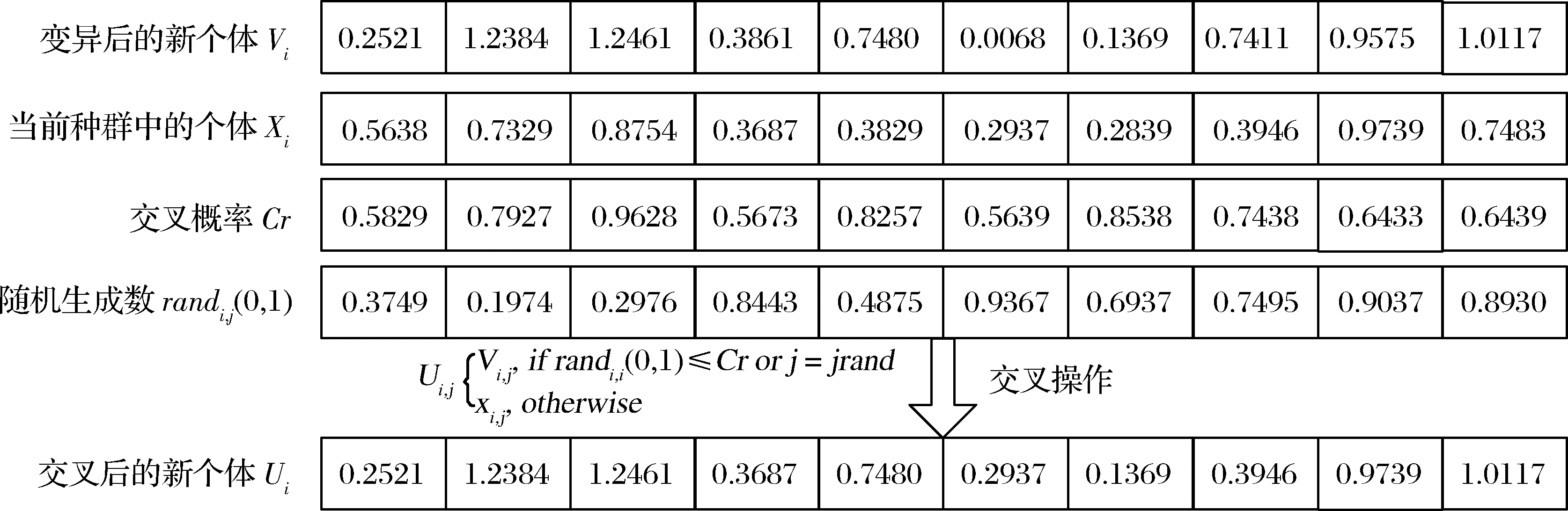
图3 染色体交叉操作示意图

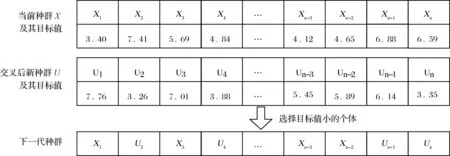
图4 种群选择操作示意图

本文采用平均年限法对油套管进行折旧。由于鄂南油区油套管在油井的放置年限为五年，没超过五年的油套管可回收维护供油井使用，放置超过五年的无法继续使用。油套管的折旧率公式为：

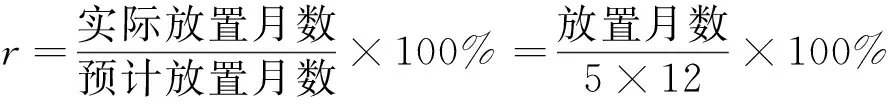
(11)

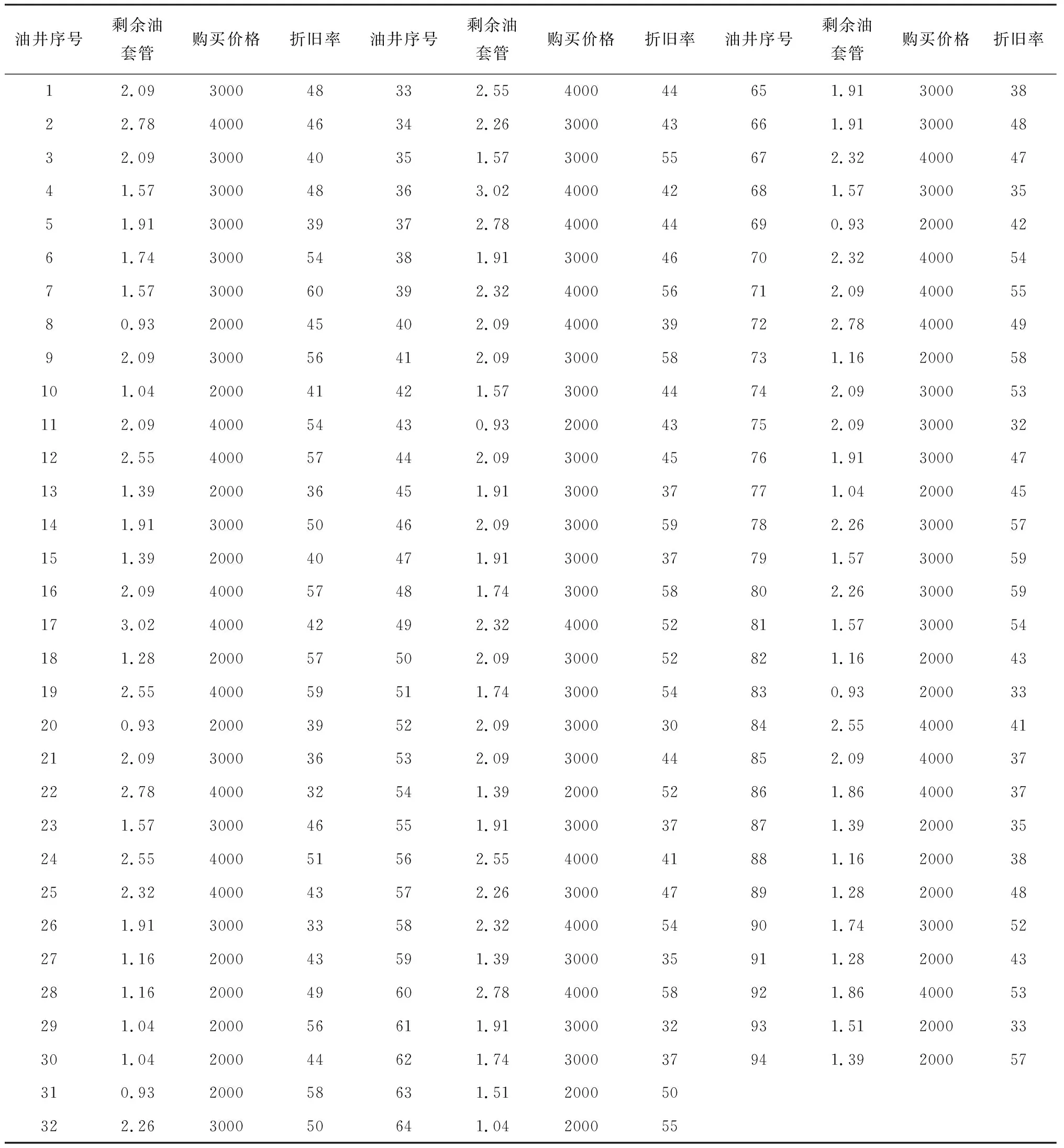
表4 油井的剩余油套管的量及折旧率

注：剩余油套管的单位为：吨；购买价格的单位为：元；折旧率的单位为%。

由表4数据可求得，待回收油套管的当前价值15.03万元。回收油套管的车辆类型共有三种，其载重量分别为4吨、10吨和15吨。在路径优化过程中，当车辆装载率达到装载阈值时，优先选择载重量大的车型安排路径；当三种车型的装载率均未达到装载阈值时，优先选择装载率最大的车型安排路径。本文油套管回收过程中车辆的运输距离数据来源于回收站与油井、油井与油井间的实际驾车距离(由于距离矩阵维度较大，本文不再具体展示)，而非两点间的欧氏距离。

4.2 参数测试

为了检验本文设计的jDE_Niche算法的优化能力，首先分别使用遗传算法(GA)、基本差分演化算法(DE)、参数自适应差分演化算法(jDE)和本文的jDE_Niche算法求解第二部分的模型，并比较不同算法的求解结果。其中不同算法求解过程中种群大小、迭代次数等参数取值相同，采用相同的编码、解码方式，变异模式和交叉模式，求解结果见表5。

表5 算法求解结果的比较

如表5所示，jDE_Niche算法比遗传算法花费更短的时间，求解得到更优的结果，只有装载率稍低于GA的求解结果；算法的收敛效果对比如图5所示，从图中可以看出本文算法的收敛速度更快。jDE_Niche算法较DE和jDE对装载率有小幅度的提高，求解过程花费了更长的时间，但其求解所得费用较DE降低了31.6%，较jDE降低了近11%。所以，本文设计的算法在较小时间代价下取得了更优的结果，说明了本文对差分演化算法的改进是合理的，且改进后的算法能有效地求解油田VRP。

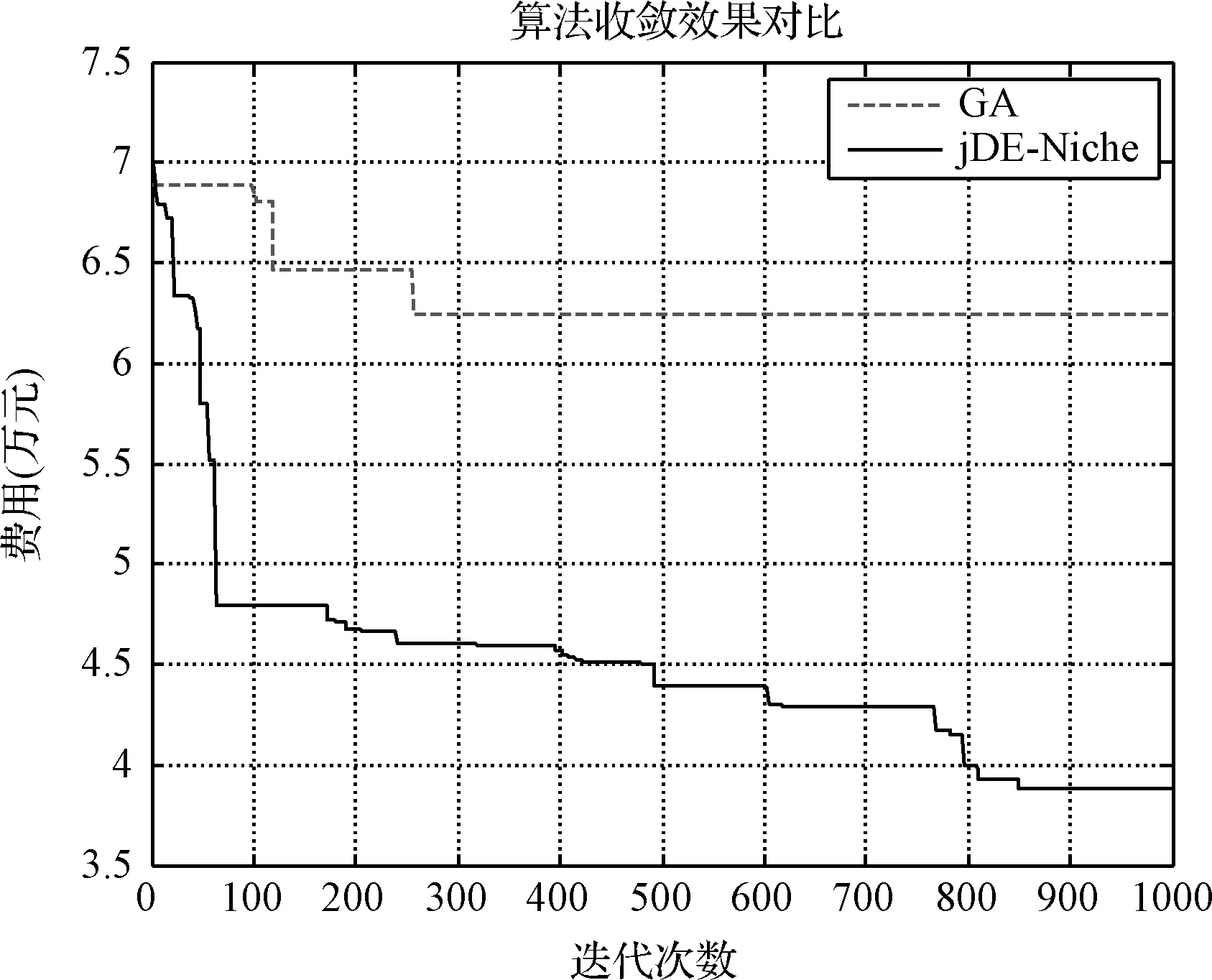
图5 算法的收敛效果对比图

在算法设计部分，本文介绍了两种染色体解码方式，首先对两种解码方式进行测试，并比较其求解效率。对于现有的94口油井的油套管回收问题，算法的部分参数如表6所示，采用本文3.1部分介绍的两种不同解码方式(其中第一种方式的装载量阈值取90%)，计算求得相应的目标函数值(总费用)、平均装载率和求解时间，结果见表7。

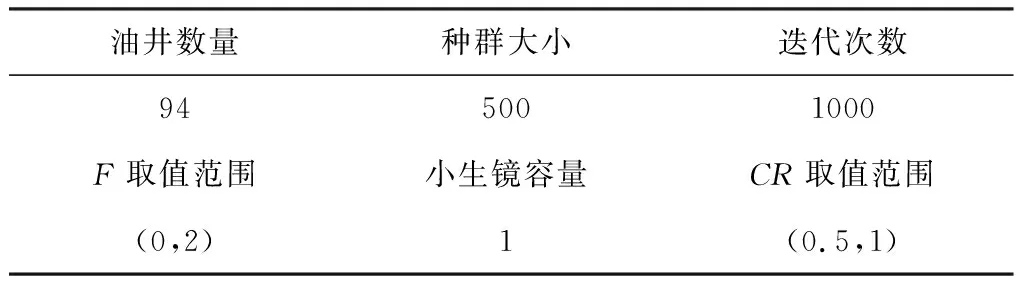
表6 算法相关参数设置

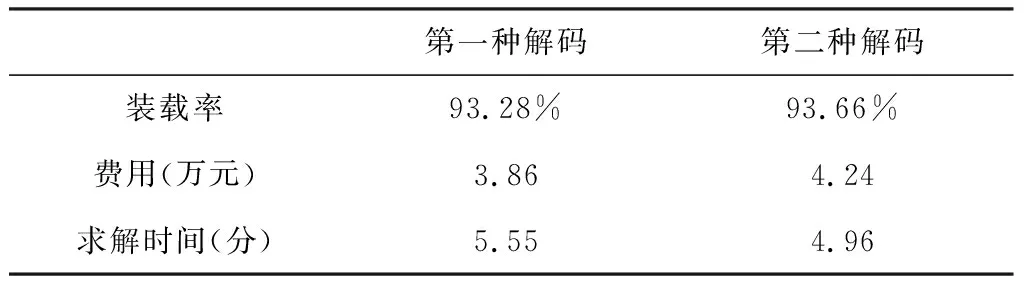
表7 两种解码方式的计算结果

如表7所示，两种解码方式得到的车辆平均装载率均超过93%，没有明显的差别；第一种解码方式求得的费用较第二种解码方式改进了约9%；显然，第一种解码方式需要更多的求解时间。对于装载率，两种解码方式都没有明显的优势；就费用而言，本文第一种解码方式求得的解优于第二种解码方式，基于此，本文采用第一种解码方式，并测试不同的装载率阈值设置对算法求解效果的影响，即其他参数不变，以装载率阈值为唯一可变参数求解，结果见表8。

由表8可知，不同的装载率阈值取值，车辆的平均装载率均超过91%，这说明在当前的算法设置中，装载率阈值的取值对车辆平均装载率的影响不大。费用受装载率阈值的影响表现为：阈值小于等于60%时，费用均超过4万元；阈值大于等于70%时，费用基本保持一致，为3.85或3.86万元。装载率阈值为70%、80%和90%时费用更低，取90%车辆的平均装载率更高，且在实际优化过程中倾向于设置更高的装载率阈值以确保车辆装载率，所以本文取装载率阈值为90%。

清除小生镜技术中的参数——小生镜半径的取值为(0,1)，所以本文对小生镜半径分别取0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8和0.9，求解结果见表9。

表8 装载率阈值不同取值情况下的计算结果

表9 小生镜半径不同取值情况下的计算结果

由表9中费用随小生镜半径取值不同的变化趋势来看，当小生镜半径取值为0.2和0.8时，费用较低；而且，小生镜半径取0.8时车辆平均装载率较高，所以本文小生镜半径取值为0.8。

综上所述，本文采用3.1部分所介绍的第一种解码方式，取装载率阈值为90%，小生境半径为0.8，其他参数如表6所示，求解鄂南油区油套管回收VRP。

4.3 结果分析

本文设计的jDE_Niche算法花费5.57分计算得油套管回收方案(见表10)，其中总运输费用为3.72万元，远低于待回收油套管的价值15.03万元。算法迭代过程中目标函数的收敛情况见图6。

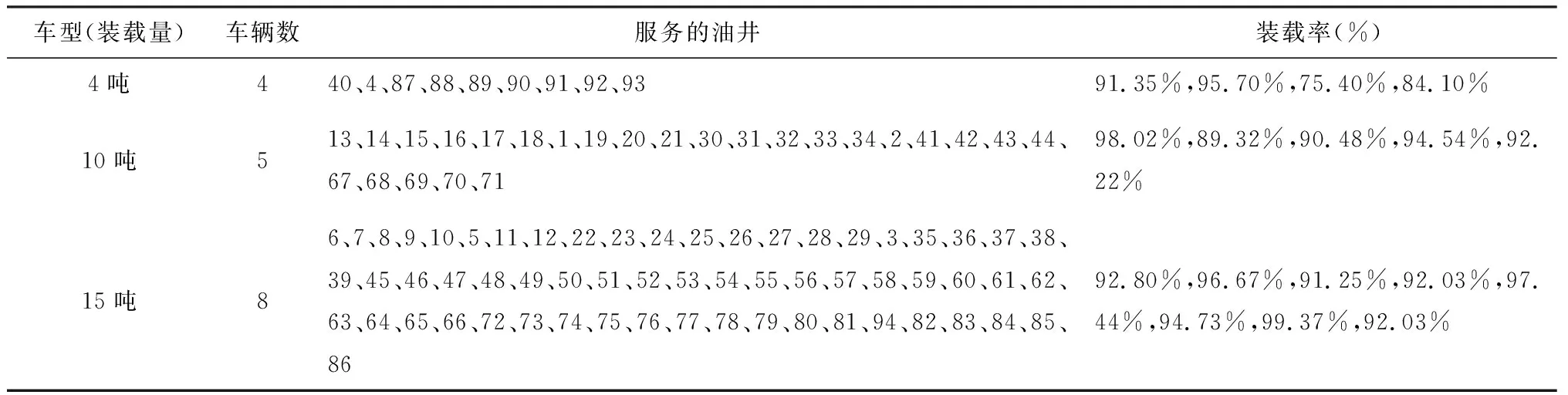
表10 油套管的回收方案

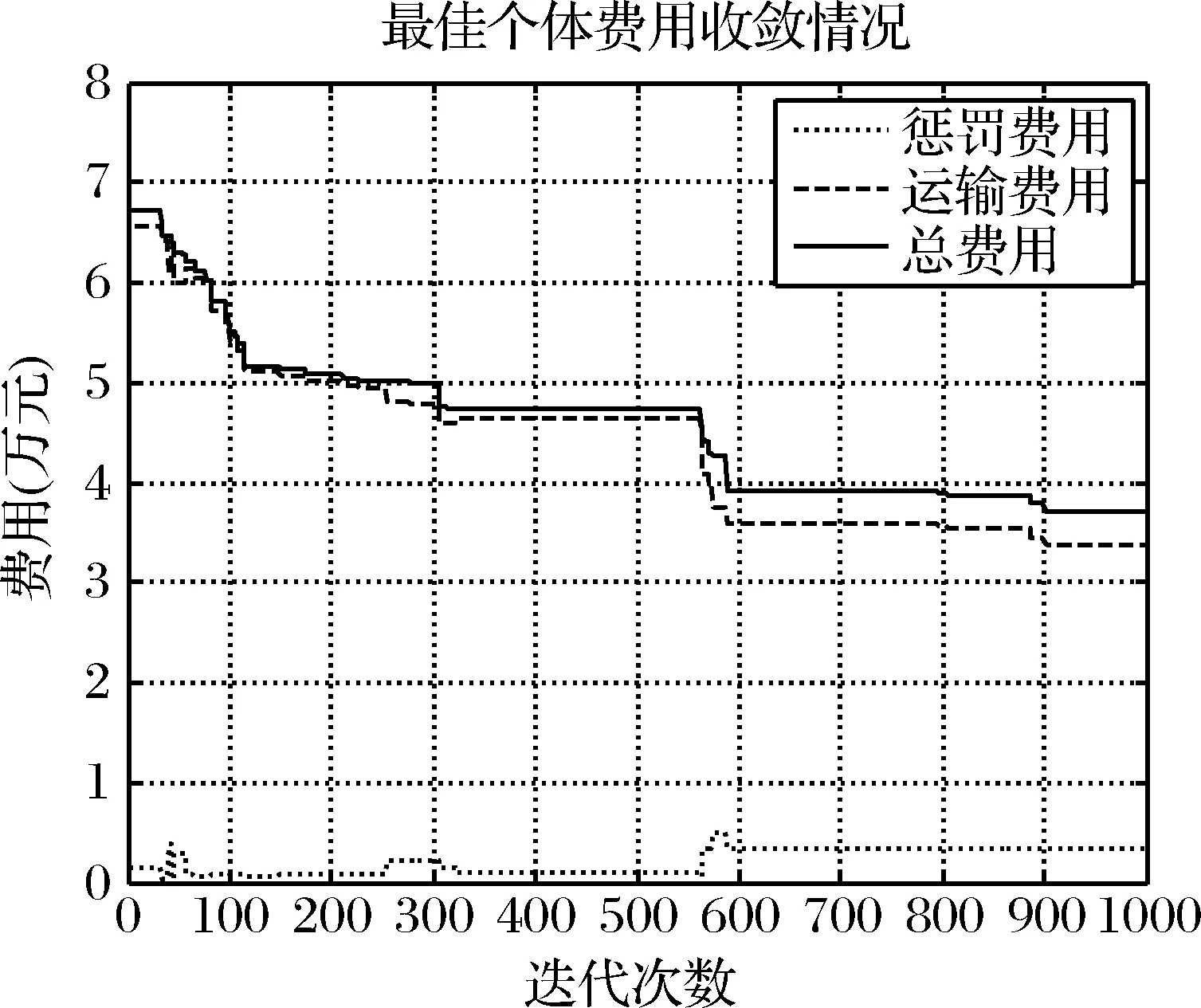
图6 最优目标函数的收敛情况

图6中总费用逐渐得到优化，最终的优化结果为3.72万元。表10中第一列是车型，第二列是该车型使用的车辆数，第三列是该车型所有车辆服务的油井，第四列是每辆车对应的装载率。此次回收油套管共需17辆车，平均装载率为92.2%。在回收方案中，不同的车型负责的路径数量存在差异性，这与油套管回收站的位置、油井位置和每口油井油套管的剩余量有关。

5 灵敏度分析

在优化模型的过程中，首先要求确定模型中的输入参数。本文取油田某一情景下的问题进行优化，当情景发生变化，输入参数也会随之变化，此时模型可能会失效。为了验证模型的鲁棒性，本文进行灵敏度分析。灵敏度分析是检测输入参数变化时模型的求解结果。

5.1 费用分析

为了检测运输价格对模型结果的影响，本文随机改变运输价格为：现有运输单价×α，α是一个随机值且α∈[0.5，1.5]。当α接近于1，表示运输单价变化小；当α=0.5，表示运输单价仅是当前实际单价的一半；当α=1.5，表示运输单价增加了一半。结果见表11和图7。

表11 运输单价的变化对求解结果的影响

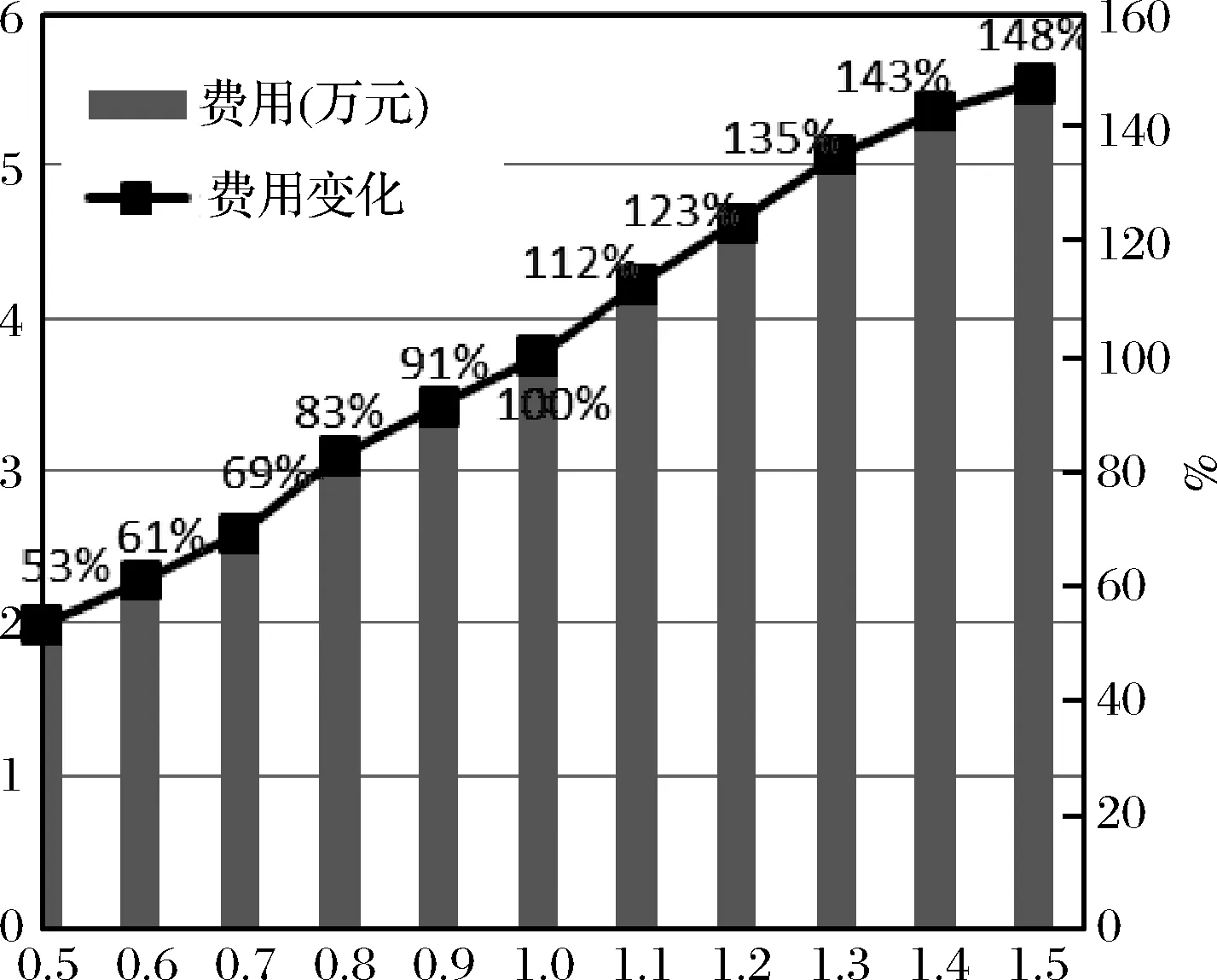
图7 运输单价的变化对求解结果的影响

如表11所示，车辆数、装载率和求解时间不受运输单价变化的影响。图7横坐标表示α的取值，左边纵坐标表示费用，右边纵坐标表示费用的变化率。图7显示费用增减的比例与运输单价的增减比例基本一致。

5.2 需求分析

为了检测各油井待回收油套管的量对模型结果的影响，本文随机改变各油井待回收油套管的量为：现有待回收量×β，β是一个随机值且β∈[0.5，1.5]。当β接近于1，表示待回收油套管的量变化小；当β=0.5，表示待回收油套管仅是实际待回收量的一半；当β=1.5，表示待回收油套管是实际待回收量的1.5倍。结果见表12和图8。

表12 待回收油套管的变化对求解结果的影响

图8 待回收油套管量的变化对求解结果的影响

图8横坐标表示β的取值，纵坐标表示所求结果的变化率。表12和图8显示待回收油套管量的变化对回收油套管所需车辆数目的影响最大，且其变化幅度较大。当β<1时，车辆的平均装载率较高，β>1时，车辆的装载率下降，但总的变化幅度较小。费用和求解时间都是随着β的取值变化小幅上升，且当0.9≤β≤1.3时，费用变化较小，这表示当油井待回收油套管的量在[当前待回收量×0.9，当前待回收量×1.3]这个范围内时，油套管回收费用变化不大。

6 结语

现有的油田物流系统的研究中，油田逆向物流VRP的研究较少。本文首先考虑油井剩余油套管的回收价值构建了油套管回收VRP模型，设计jDE_Niche求解数学模型，然后以中石化华北石油局鄂南油区94口油井的油套管回收问题为例，优化分析。本文的研究结果表明：(1)本文设计的算法用于求解油田实际问题时在求解时间和收敛速度上具有明显的优势。(2)在算法优化过程中采用本文设计的第一种解码方式，将装载率阈值设置为90%、小生镜半径设置为0.8时，算法的效果更优。(3)车辆数、装载率和求解时间不受运输单价变化的影响，只有回收费用直接受运输单价影响，且随运输单价同比例增减。(4)待回收油套管量的增加，会引起车辆装载率降低，回收费用、优化时间和车辆数目增加，其中所需车辆数目的变化最大。本文的模型和算法对于进一步补充和完善逆向物流VRP有一定的意义，也对油田行业有节约资源、降低成本的现实意义；其中本文的模型适用于回收成本较高逆向VRP，jDE_Niche算法可用于求解实际应用VRP。在未来的研究工作中，将在模型中考虑车辆数量约束、油套管回收量的动态变化、考虑油套管回收后的维护费用等特征；而且也会对算法的参数(如小生镜容量等)进行更多的测算。

参考文献：

[1] Dantzig G B, Ramser J H. The truck dispatching problem[J]. Management Science, 1959, 6(1): 80-91.

[2] 刘云忠,宣慧玉. 车辆路径问题的模型及算法研究综述[J]. 管理工程学报,2005,19(1): 124-130.

[3] Eksioglu B, Vural A V, Reisman A. The vehicle routing problem: A taxonomic review[J]. Computers & Industrial Engineering, 2009, 57(4): 1472-1483.

[4] Kara B Y, Verter V. Designing a road network for hazardous materials transportation[J]. Transportation Science, 2004, 38(2): 188-196.

[5] Zheng Yujun, Ling Haifeng. Emergency transportation planning in disaster relief supply chain management: A cooperative fuzzy optimization approach[J]. Soft Computing, 2013, 17(7): 1301-1314.

[6] 李琳, 刘士新, 唐加福. B2C 环境下带预约时间的车辆路径问题及多目标优化蚁群算法[J]. 控制理论与应用, 2011, 28(1): 87-93.

[7] Fleischmann M, Bloemhof-Ruwaard J M, Dekker R, et al. Quantitative models for reverse logistics: A review[J]. European journal of operational research, 1997, 103(1): 1-17.

[8] 张群,卫李蓉. 逆向物流网络设计研究进展[J]. 中国管理科学,2016,24(9):165-176.

[9] Savelsbergh M W P, Sol M. The general pickup and delivery problem[J]. Transportation Science, 1995, 29(1): 17-29.

[10] Männel D, Bortfeldt A. A hybrid algorithm for the vehicle routing problem with pickup and delivery and three-dimensional loading constraints[J]. European Journal of Operational Research, 2016, 254(3): 840-858.

[11] 罗叶新, 张宗杰，王喜，等. 油田地面集输系统布局优化模型[J]. 油气储运, 2014, 33(9): 1004-1009.

[12] Wei L, Jiang H, Liu Y. Hybrid Genetic-Simulated Annealing Algorithm of Location-Allocation Optimization of Looped Gathering and Transportation Pipe Network[C]//Proceedings of the Fifth International Conference on Natural Computation,Tianjin, China, August 14-16,2009.

[13] 达列雄. 基于HS算法的油田事故应急资源调度系统[J]. 计算机与数字工程, 2015, 43(02): 232-234.

[14] 王鑫. 基于四层架构的网络化共同配送体系研究——以胜利油田物流配送为例[J]. 物流技术, 2014,(3): 67-71.

[15] 戴永寿, 李韶光, 李立刚, 等. 基于改进 k-means 和遗传算法的油田特种车辆优化调度[J]. 计算机应用, 2016, 36(S1): 86-89.

[16] Hennig F, Nygreen B, Furman K C, et al. Alternative approaches to the crude oil tanker routing and scheduling problem with split pickup and split delivery[J]. European Journal of Operational Research, 2015, 243(1): 41-51.

[17] Cuesta E F, Andersson H, Fagerholt K, et al. Vessel routing with pickups and deliveries: An application to the supply of offshore oil platforms[J]. Computers & Operations Research, 2017, 79: 140-147.

[18] Carotenuto P, Giordani S, Massari S, et al. Periodic capacitated vehicle routing for retail distribution of fuel oils[J]. Transportation Research Procedia, 2015, 10: 735-744.

[19] 杨娟,袁可红，郭海湘，等. 煤矿危险物资多趟配送车辆路径问题[J]. 系统管理学报, 2013, 22(5): 728-736.

[20] 梁全胜, 王雪飞, 梁卫卫, 等. 鄂尔多斯盆地南部中生界原油地球化学特征及油源分析[J]. 高校地质学报, 2014, 20(2): 309-316.

[21] Storn R, Price K. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.

[22] Ali M M, Törn A. Population set-based global optimization algorithms: Some modifications and numerical studies[J]. Computers & Operations Research, 2004, 31(10): 1703-1725.