直线参数方程的推导与参数t的意义

辽宁省抚顺市德才高级中学 陈贵军

笔者在从事一线教学过程中，讲授高中数学人教B版选修4-4 《极坐标与参数方程》时，发现同学们在2.2.1直线的参数方程中，应用参数t的意义求解问题始终不能得心应手，不少同学只是机械的记忆与模仿例题去解题，不知其所以然。笔者认为，其直接原因是同学对参数t意义理解不透彻，而导致这种现象的根本原因是直线参数方程的推导过程中，没有突出参数t的意义造成的。本文中，介绍一下笔者认为更为合理的直线参数方程的推导过程，希望能够对各位老师或同学研究直线的参数方程略有帮助，若有不当之处欢迎各位老师和同学批评指正。

首先，我们先回顾曲线的参数方程的定义：

设在平面上取定了一个直角坐标系xoy把坐标表示为第三个变量t的函数，并且对于t的每一个值，由所确定的点都在一条曲线C上，而曲线C上的任意一点上都可由t得某个值通过得到，则称就叫做这条曲线的参数方程。其中，变量t叫做参数。

下面，我们来研究直线的参数方程及其应用。

已知直线l经过定点，倾斜角为，设直线l上异于定点的任意一点。

若点M位于定点M0的上侧，如图1，设，则有，从而始终有下式成立。

若点M位于定点M0的下侧，如图2，设，则有，从而始终有下式成立。

当直线主要经过二、四象限时，研究方法相同。

结合以上情况，我们就可以得到直线的参数方程：

参数t的几何意义：

（1）|t|表示参数t对应的点到M定点M0的距离，即。

（2）因为倾斜角，所以，因此，当参数时，表示点M位于定点M0的上侧；当参数时，表示点M位于定点M0的下侧。

新知体验：

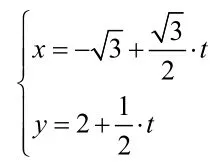
(1)分别求时对应的点

(2)求直线l的倾斜角；

(3)求直线l上的点对应的参数t，并说明t的几何意义.

例题2：已知直线L经过点、倾斜角为，

1）求直线l的参数方程；

（2）求直线l和直线的交点到点的距离。

二、常用结论：

已知，直线l：(t为参数)与曲线交于两点A,B两点，对应的参数分别为ti,t2，则

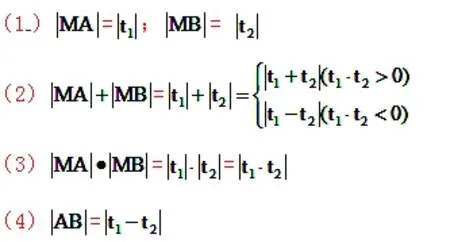
说明：因为参数方程本质上仍为直角坐标方程，因此中点公式依然成立。在本文中就不加以证明了。

例3：经过点，倾斜角为的直线l与圆相交于两点A,B，求的值。

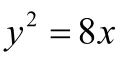
(1)求

(2)求的中点M的坐标及.（答案：16，(6,4)，