浅谈初中数学教学中合情推理能力的培养

上海市第五十四中学 苗 伟

数学对发展推理能力的作用，人们早就深信不疑。但是，长期以来数学教学注重采用“形式化”的方式发展学生的演绎推理能力，忽视了合情推理能力的培养。应当指出，数学需要演绎推理，更需要合情推理。科学结论（包括数学的定理、法则、公式等）的发现往往发端于对事物的观察、比较、归纳、类比即通过合情推理提出猜想，然后再通过演绎推理证明猜想正确或错误。

波利亚说，数学的创造过程与任何其它知识的创造过程一样，在证明一个定理之前，先得猜想、发现出这个定理的内容，在完全作出证明之前，先得不断检验、完善、修改所提出的猜想，还得推测证明的思路，你先得把观察到的结果加以综合，然后加以类比，你得一次又一次地进行尝试。在这一系列的过程中，需要充分运用的不是论证推理，而是合情推理。

《数学课程标准（2011年版）》指出：“教师在教学过程中，引导学生通过观察、尝试、估算、归纳、类比、画图等活动进行合情推理，发现一些规律，猜测某些结论，增强发现和提出问题的能力，以及解决问题的基本思路”。

下面，笔者结合自己多年的教学实践，从课内课外两个方面浅谈如何培养学生的合情推理能力。

一、在课内教学中创设问题情境培养学生的合情推理能力

【实例1】 分数除法法则

发现结论：

甲数除以乙数（0除外），等于甲数乘以乙数的倒数。

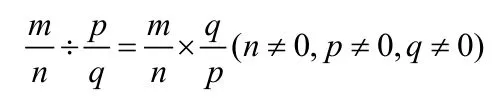
证明结论：

根据除法的商不变性质，

【实例2】一元二次方程的根与系数的关系

发现结论：

①填写下列表格

观察上表，你能得到什么启发？

②猜想：关于X的一元二次方程， x1、x2是其两个实根。，

证明结论：

对于一元二次方程， x1、x2是其两个实根。

【实例3】切线长定理

发现结论：

在透明纸上画出图（1）：设P是⊙O外任意一点，PA、PB是⊙O的两条切线，A、B是切点。

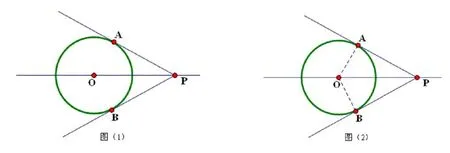
让学生操作：沿直线OP将图（1）对折，启发学生思考，或者组织学生交流。

通过操作，追问学生能得出什么结论？

学生应该较容易发现：.这是通过实例发现图形性质的过程，实际上，这也是证明的基本思路。启发学生由特殊到一般，通过合情推理得出切线长定理的结论：过圆外一点所画的圆的两条切线长相等。

证明结论：

如图（2），联结OA、OB，因为PA、PB是 ⊙O的切线，所以,即△POA和△POB都是直角三角形。又因为OA=OB且OP=OP，所以△POA和△POB全等。于是有 PA=PB，

㉑赵海乐:《是国际造法还是国家间契约——“竞争中立”国际规则形成之惑》，《安徽大学学报》(哲学社会科学版)2015年第1期。

由此可见，数学教学过程中必须给学生提供探索交流的空间与时间，组织引导学生“经历观察、实验、猜想、证明等数学活动。”把推理能力的培养有机地融合在数学教学活动的各个过程中。

只要教师有了这样的意识，不仅在课内，在课外的习题中也经常碰到这样的例子。

如：

观察：12+21=33

23+32=55

34+43=77

①你发现了什么结论？请写出你的观点。

②你能证明你得到的结论吗？

解：①一个两位数将个位数字与十位数字对调后，得到新数与原数的和，一定能被11整除。

验证：51+15=66=6×11

②证明：设这个两位数为（10x+y），则新数为(10y+x)。

其解答过程有计算、观察、归纳、猜想、证明等过程，既培养了学生合情推理能力，也培养了学生演绎推理的能力。

二、在课外学习中设计分层作业培养学生的合情推理能力

林崇德认为推理能力分为四级水平：第一级，直接推理水平。具体表现为套公式、用单个概念直接推出结论。第二级，间接推理水平。需要对条件进行变换、化归，多步骤地进行推理得出结论。第三级，迂回推理水平。分析前提，提出假设，并进行反复验证后才导出结论。第四级，综合推理水平。能根据需要选择相应的推理方式，推理过程简练、合理。既然学生的推理能力水平不同，就有必要通过作业分层，有针对性的发展学生的推理能力。

一般认为，分层作业是指优化的弹性作业结构，它针对学生的学习水平层次进行分类，目的是使不同层次学生的学习得到不同程度的提高。分层作业是与统一要求的作业相对立的一种作业类型。

分层作业的设计也就是要在合理地对学生分层的基础上，体现优等生、中等生和学困生的学习差异，保护每一个学习群体的心智发育水准，安排与其学习能力、掌握能力范围内相符合的适度作业。

总之，培养合情推理的基本途径是：观察为基础；联想为桥梁；想象为动力；创新为目的。要设置现实的、有意义的、富有挑战性的问题，引导学生参与“过程”；要精心组织、设计形式多样的分层作业，并真正鼓励学生、尊重学生、学生合作。这样，就能拓宽发展学生合情推理能力的空间，从而有效地发展学生的合情推理能力。对于学生，它不但能使学生学到知识，会解决问题，而且能使学生掌握在新问题出现时该如何应对的思想方法。对于老师，研究合情推理教学能提高自己的业务水平，增加课堂教学的趣味性，使教学更加有条理。