《二次函数的应用——抛物线中的线段》教学设计

湖南省衡东县霞流镇中学 罗祝岐

学情分析：

农村的初中学生多为留守儿童，学习基础较差，而且参差不齐。针对学生特点，因此本节课每组题都有两个环节。一是落实求二次函数最值的复习、检测及过手，二是二次函数的建模。循序渐进地先过手基本知识点再进行建模。

学习目标：

1.对全章的主要数学思想和方法有一个全面、系统的掌握；

2.结合中考固定题型，能根据中考题型中的已知条件分析问题，应用这些数学思想方法，把问题落脚到某一具体的知识点（公式法、配方法、二次函数的顶点坐标、对称轴、最值），并解决抛物线中的线段问题。

3.培养小组合作的精神。

学习重点：

1.对实际问题进行建模（函数）

2.掌握分别用公式法与配方法求二次函数的顶点坐标、对称轴、最值。

学习难点：

如何把已知问题进行建模（函数）

导学过程：

一、自主探究（课前完成）

1.分别用公式法和配方法，求出下列二次函数对应抛物线的顶点坐标，对称轴，及x为何值时， y有最值，最值是多少？

（1）y=x2-2 x+3（2）y=-2x2-8x+2

2.(2014重庆中考25题改编)

如图，抛物线y=-x2-2x+3 的图象与x轴交于A、B两点

（ 点A在点B的左边），与y轴交于点C，点D为抛物线的顶点。

（1）求点A、B、C的坐标；

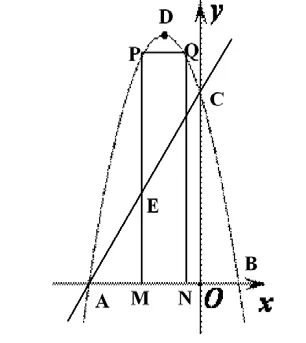
(2) 点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，如图，点P在点Q左边，求矩形PMNQ的最大周长为多少，并求此时点M，点E,点P的坐标。

【（2）的变式训练】点M为线段AB上一点（点M不与点A、B重合），过点M作

x轴的垂线，与直线AC交于点E，求PE的最大值，并求此时点E的坐标。

【设计理由】二次函数是中考必考，前面两节课我们明确了考点，大多数同学掌握了知识点。本课时来攻克中考当中二次函数的固定题型,故设计第2题。2题（2）小题的变式及后面的课堂检测都是设计的列“长度相关”的代数式。家庭作业则设计的列“面积相关”的代数式。变式的设计深入浅出，利于学生过手方法的同时增加自信。又由于此类题中涉及到找二次函数顶点，求最值是计算易错点，所以特意设计第1题。

【使用说明】学生独立复习题目相关知识点，课前独立完成。

二、幻灯片引入(2分钟)

播放一组上学期做过的半期，期末练习及考试试卷，凸显出25题

【设计理由】引导学生从做过的套题中，认识到本节课训练题型的重要。

【使用说明】播放幻灯片，引导学生发现。

三、合作探究、小组展示（时间：18分钟）

【设计理由】培养小组学习共同体，利用小组的力量，首先自己解决学生互助就能解决的问题，然后找出需要老师帮助解决的问题

【使用说明】

1.小组讨论自学内容10分钟，组长组织对答案，并收集本组未解决的问题

2.各小组抽牌得到一个序号，一个序号对应一个自学内容

3.讨论七八分钟的时候老师开始收集各小组未解决的问题，老师确定哪些自学内容需要展评。

4.抽到需要展评题目的小组派同学展评，展评时间8分钟。展评成功后小组加相应的分值（分别为1,2,3分），抽到全班基本已经过手，不需要展评自学内容的小组直接加1分。

四、达标检测，小组评比（时间：18分钟）

1.求出二次函数y=-x2+5x对应抛物线的顶点坐标，对称轴，及x为何值时， y有最值，最值是多少？

2.（2013重庆中考25题改编）如图，已知抛物线y=x2+bx+c的图象与x轴的一个交点为B（5，0），另一个交点为A，且与y轴交于点C（0，5）.

（1）求直线BC与抛物线的解析式；

（2）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值。

【设计理由】检测学生掌握情况， 1题为2题打好了计算基础，是2题的计算易错点，2题是本节课重点也是难点，需要根据已知条件分析问题，把问题落脚到某一具体的知识点上。

【使用说明】

1.独立完成10分钟。

2.老师简要评讲答案，交换批改，组长出错扣1分，小组四人及以上正确加1分。批改时间4分钟。

3.同学们自己改错，组长下位询问每个组员的掌握情况，作下记录，课后跟进帮助。时间4分钟。

五、课时小结（时间：2分钟）

【设计理由】归纳总结，回忆巩固知识点的同时形成方法。

【使用说明】从两方面引导学生归纳：1.知识点；2.思想方法

六、作业布置

如图，抛物线y=ax2+bx+6与x轴交于A、B两点，与y轴交于点C，已知A(-1,0)、B(3,0)。

(1)求抛物线及直线BC的解析式；

(2) M为抛物线上一动点，过点M作y轴的平行线交直线BC于D,求当MN=2.5时点M的坐标。

(3)若P为抛物线上位于直线BC上方的一点，求△PBC面积S的最大值，

【设计理由】类比解决抛物线中线段问题的思想方法进行自学，尝试独立探索解决抛物线中的面积问题，不但进一步巩固所学知识方法， 同时也为下节课的学习内容展开自学探究，有承上启下的作用。