K均值聚类算法的研究与优化

陶 莹，杨 锋，刘 洋，戴 兵

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

数据挖掘在实际应用中的主要任务之一是聚类分析，其是数据挖掘中一个很热门的研究领域，同时与其他学科的研究方向有很大的交叉性[1]。聚类分析可以发现数据隐含的结构，对数据进行自动归类，从而得到数据的大致分布，在诸多领域为决策提供支持信息[2]。

K均值聚类算法是聚类分析方法中一种基本的划分式方法[3]。由于该算法简便易懂，且计算速度较快，通常被作为大样本聚类分析的首选算法[4]。

但是一般的K均值聚类算法初始聚类中心的选择是随机的，这样会导致聚类结果的不稳定。而且算法中k的值需要人为提前设定，k值设定的合理与否会直接影响聚类的效果[5]。此外，噪声和离群点也会对聚类效果产生影响，使得聚类中心偏离主要数据区域[6]。因此，文中针对K均值聚类算法的随机性较强的特点进行改进。

1 K均值聚类算法

1.1 算法基本思想

首先在整个数据集中任意选择k个数据作为初始聚类中心，然后计算其他数据对象与k个聚类中心的距离，将数据对象划分到距离最近的聚类中心所在的聚类域。所有数据划分好后，重新计算k个聚类中每个聚类的全部数据对象的平均值，该平均值所在的数据点成为新的聚类中心。最后进行多次迭代，直到连续两次的聚类中心相同，说明此时数据对象类别划分完毕，即得到k个聚类[7]。

1.2 算法评价准则—误差平方和

评价聚类效果，可以定义一个数据对象和其所在聚类域的目标函数。通过目标函数的取值情况评价聚类效果[8]。常用的聚类算法评价准则是中心误差的平方和，即：

(1)

其中，Xu是数据u的全部属性值所构成的矢量；k是聚类个数；m1,m2,…,mk是k个聚类中心对应的矢量；cj是聚类中心为mj的聚类域。

聚类中心矢量mj表示为：

(2)

其中，Nj为聚类域cj中数据的个数。

式1中，目标函数J代表k个聚类里的全部数据与其聚类中心mj之间的误差平方和，值越小表明聚类中数据的集中性越好，即得到的聚类效果越好[9]。

1.3 算法局限性分析

(1)K均值聚类算法中的k值(待聚类簇的个数)必须由用户输入。

k值必须是用户最先确定，即分为多少个聚类。但是在一些实际情况下，合适的聚类数目k用户也是未知的，在这种情况下，就需要运用其他办法来获得到聚类的数目[10]。

(2)k个聚类中心的选择是随机的。

一般K均值聚类算法初始中心是随机选择的，然后进行聚类和迭代，并最终收敛达到局部最优结果[11]。因此，聚类结果对于初始中心有着严重的依赖，随机选择初始中心会造成聚类结果有很大的随机性。

(3)K均值聚类算法对于噪声和离群点数据非常敏感。

K均值聚类算法中每个聚类的中心都由每个聚类里所有数据求均值得到。当有与其他数据不一致的数据或者差异比较大的数据时，计算出的聚类的中心易受干扰，偏离主要数据区域，影响聚类效果。因此，K均值聚类算法对数据中的噪声和离群点非常敏感[12-13]。

2 全局K均值聚类算法

2.1 算法基本思想

全局K均值聚类算法从k=1的聚类开始，即先求出所有数据的聚类中心m。当k=2时，将聚类中心m作为其中一个初始聚类中心，然后依次将数据集的每个点作为另一个聚类的初始中心，即运行n次K均值聚类算法，计算误差平方和J后，取值最小的点确定为第二个聚类中心，其中聚类后得到了新的聚类中心m1，m2。如果k=3,4,…,n，以此类推[14]。

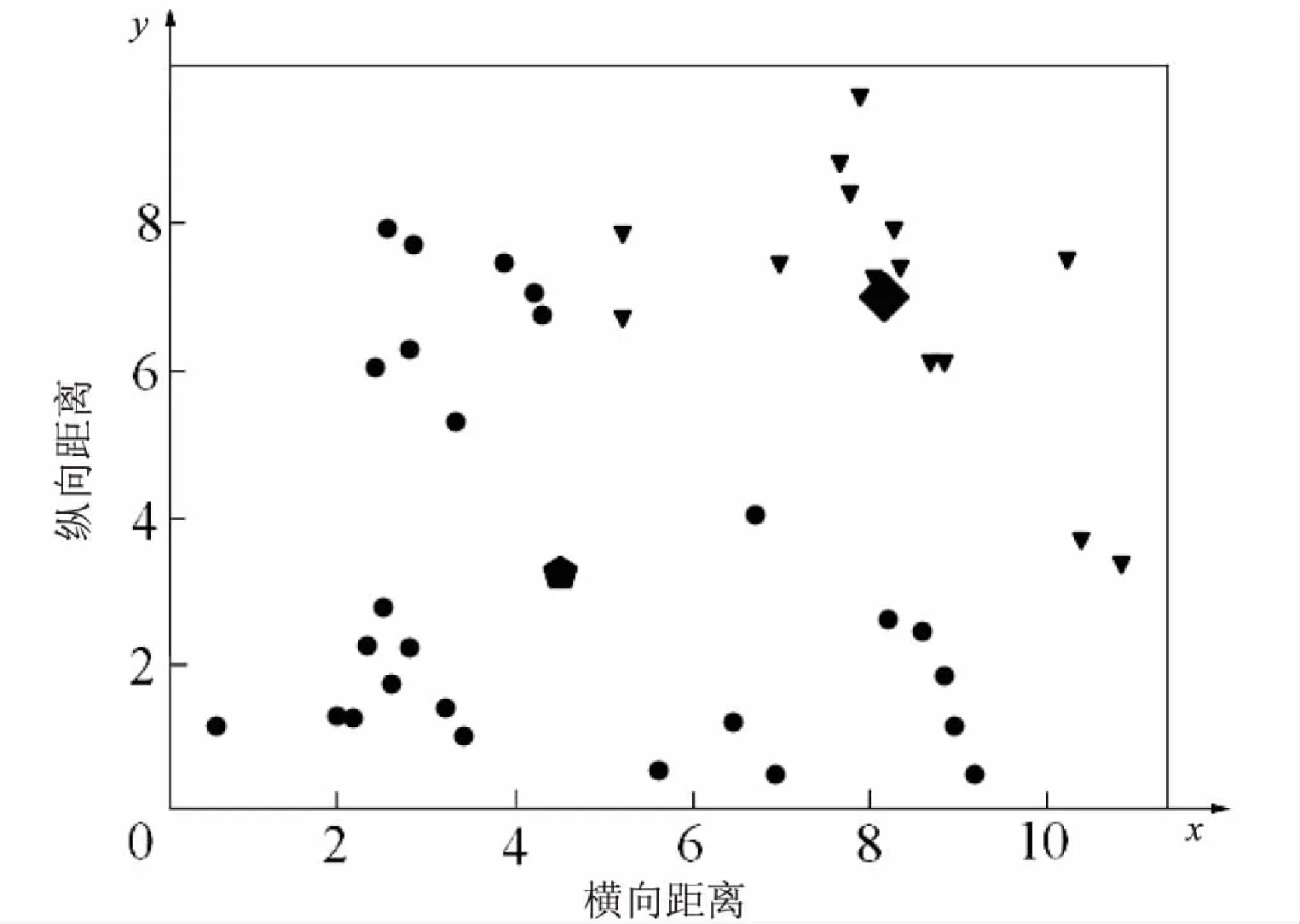
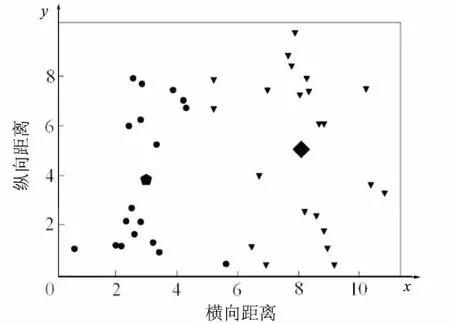
全局K均值聚类算法最终得到了所有k(k

2.2 实验数据分析

当k=2时，对40个数据重复使用K均值聚类算法得到4种不同的结果，如表1和图1～4所示。根据误差平方和评价准则，最好的实验结果是实验一，其误差平方和是112.92386462，但K均值聚类算法本身的不稳定性使得每次产生不一样的聚类结果，不一定是最优的，甚至是很差的聚类结果。

表1 K均值聚类算法4次实验结果

图1 K均值聚类结果一

图2 K均值聚类结果二

图3 K均值聚类结5三

图4 K均值聚类结果四

下面使用改进的K均值聚类算法即全局K均值聚类算法对数据进行实验。当k=1时，得到聚类中心m=[-0.20740458，0.0553751]，再用m分别和每一数据点为中心进行K均值聚类算法。实验数据见表2。

表2 全局K均值聚类算法实验数据

全局K均值聚类的结果如图5所示。

图5 全局K均值算法聚类结果

与K均值聚类算法相比，全局K均值聚类算法的误差平方和J=112.923113，改善了K均值聚类算法的随机性所导致不理想结果的可能性。全局K均值聚类算法不受初始聚类中心位置的影响，并且通过一种确定有效的方法能够最小化误差平方和。

3 结束语

聚类算法发展到今天，已经衍生出了多种算法。其中，经典的K均值算法作为划分聚类算法中最基础的算法，由于其高效性和简单性被广泛应用于各领域[16]。然而，K均值算法也有其固有的局限性，而很多针对K均值算法的改进都极大地降低了算法本身的性能，这显然是得不偿失的[17]。对此，文中对K均值聚类算法进行了改进，降低了算法的不稳定性，提高了聚类的有效性。

参考文献：

[1] 周 涛,陆惠玲.数据挖掘中聚类算法研究进展[J].计算机工程与应用,2012,48(12):100-111.

[2] 盘俊良,石跃祥,李娉婷.一种新的粒子群优化聚类方法[J].计算机工程与应用,2012,48(8):179-181.

[3] ABDEYAZDAN M.Data clustering based on hybrid K-harmonic means and modifier imperialist competitive algorithm[J].Journal of Supercomputing,2014,68(2):574-598.

[4] HUNG C H,CHIOU H M,YANG Weining,et al.Candidate groups search for K-harmonic means data clustering[J].Applied Mathematical Modelling,2013,37(24):10123-10128.

[5] 丁祥武,郭 涛,王 梅,等.一种大规模分类数据聚类算法及其并行实现[J].计算机研究与发展,2016,53(5):1063-1071.

[6] 万 静,张 义,何云斌,等.基于KD-树和K-means动态聚类方法研究[J].计算机应用研究,2015,32(12):3590-3595.

[7] 罗军锋,锁志海.一种基于密度的k-means聚类算法[J].微电子学与计算机,2014,31(10):28-31.

[8] 王 涛,卿 鹏,魏 迪,等.基于聚类分析的进程拓扑映射优化[J].计算机学报,2015,38(5):1044-1055.

[9] SAHOO A K,ZUO M J,TIWARI M K,et al.A data clustering algorithm for stratified data partitioning in artificial neural network[J].Expert Systems with Applications,2012,39(8):7004-7014.

[10] 贾洪杰,丁世飞,史忠植.求解大规模谱聚类的近似加权核k-means算法[J].软件学报,2015,26(11):2836-2846.

[11] 朱建宇.K均值算法研究及其应用[D].大连:大连理工大学,2013.

[12] GÜNGÖR E,ÖZMEN A.Distance and density based clustering algorithm using Gaussian kernel[J].Expert Systems with Applications,2017,69:10-20.

[13] 赵 丽.全局K-均值聚类算法研究与改进[D].西安:西安电子科技大学,2013.

[14] 雷小锋,谢昆青,林 帆,等.一种基于K-Means局部最优性的高效聚类算法[J].软件学报,2008,19(7):1683-1692.

[15] 张建萍.基于计算智能技术的聚类分析研究与应用[D].济南:山东师范大学,2014.

[16] AHMAD A,HASHMI S.K-harmonic means type clustering algorithm for mixed datasets[J].Applied Soft Computing,2016,48:39-49.

[17] TU Chunhao,JIAO Shuo,KOH W Y,et al.Comparison of clustering algorithms on generalized propensity score in observational studies:a simulation study[J].Journal of Statistical Computation and Simulation,2013,83(12):2206-2218.