基于神经网络的光栅信号软件细分技术的研究

汤 攀，张厚武，何 勇

(贵州大学 计算机科学与技术学院，贵州 贵阳 550025)

1 概 述

光栅位移传感器是精密的光栅测量系统,适用于大量程的精密测量，并在医疗设备、仪器制造、机械生产、武器研制等方面起着重要作用[1]。随着精密加工技术与超精密加工技术的发展，对测量精度的要求越来越高，而常用的50线/毫米经济型的光栅传感器，它的精度为20 μm，难以达到精密测量的要求。因此需要对光栅传感器输出的信号进行细分来提高测量的精度。

朱维娜等[2]提出了一种基于DSP的光栅细分技术，以DSP为主芯片，实现对25线光栅尺不低于10倍细分计数；胡晓东等[3]提出运用FPGA为主芯片，既提高了解位移算法的正确性，也提高了运算速度；李怀琼等[4]提出了一种采用数字信号处理与软件计算的细分方法，实现莫尔条纹八细分；王冠雅等[5]提出对采集到的信号进行分析时,使用软件细分的方法,实现了光栅信号的80倍细分。但是以上的细分方法都是基于硬件实现的，实现起来复杂，并且很难对其进行扩展。

目前主流的细分技术主要有：四细分、电阻链移相细分、锁相倍频细分、幅值分割细分、神经网络细分[6-7]。将以上五种细分方法从细分倍数、优点、缺点以及应用方面进行分析对比，选择出适合的细分方法。对比分析如表1所示。

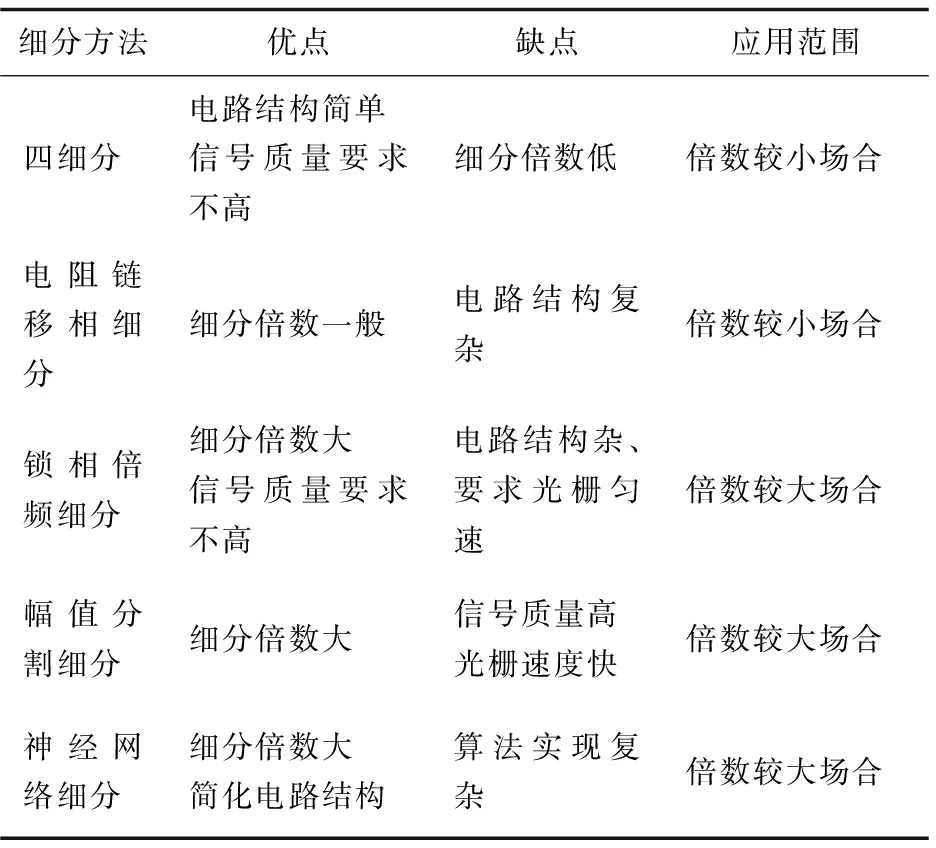
表1 光栅信号细分方法的对比分析

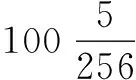
2 细分原理

2.1 测量系统总体设计

光栅传感器输出的四路相位相差90°的正弦信号送至差动放大电路，既可以消除偶次谐波的影响，也能消除直流电平带来的误差，然后得到两路相位相差90°的正弦信号，再送至整形电路将原始光栅信号转换成方波信号，将方波信号送入FPGA进行四细分、辨向和可逆计数，完成大数计数的功能，单片机读取FPGA计数器的值，并运用串口COM6传给后台；与此同时，送至AD模块进行AD采样，然后传给串口COM7，后台直接读取串口COM7的AD值，送入神经网络细分程序完成小数细分。最后结合大数值和小数值计算出总位移量。

2.2 细分原理

选用50线/mm的经济型光栅尺，光栅尺移动一条刻线相当于光栅信号移动一个周期(一个周期的正弦信号)，即移动了20 μm。通过FPGA将整形后得到与光栅信号周期一致的方波信号进行计数，即可求得所测的大数值，实现硬件四细分。设不足1/4个周期的位移值表示为d，则具体位移可表示为：

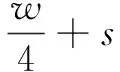
(1)

其中，k为大数计数值；s为不足1/4周期的微位移值；w为光栅的栅距。

为了获得精位移值s，需对不足1/4个周期的小数部分进行高倍细分。只能运用光栅输出的正余弦信号才能进行高倍细分。由于光栅传感器输出的正余弦信号幅值较小，若直接运用细分效果不佳，故需先对光栅输出的四路相位相差900的正弦信号进行放大处理，得到近似正弦和余弦信号：

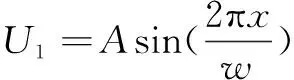
(2)

(3)

从公式中可以看出，电信号和光栅位移存在一定的函数关系，即光栅传感器移动的位移x可通过测量的电压U值计算得出。精细分就是运用光栅信号的电压幅值与位移值之间的数学关系，通过对信号进行A/D采样转换，再运用查表或者数学关系式计算出微位移[8]。文中的精细分是运用神经网络算法实现的。由于正、余弦信号线性度不好，特别是在峰值附近时，只有光栅尺的位移变化量较大才能产生一个微小的电压变化，如果直接将采集的正余弦信号作为网络输入，则从细分原理上会带来很大误差。设计用式4作为输入量：

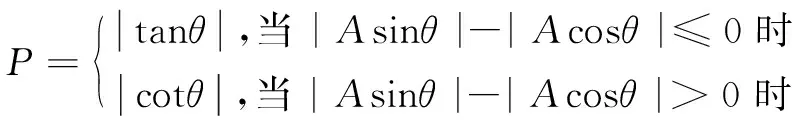
(4)

根据以上分段函数图像的对称性，|Asinθ|-|Acosθ|>0时的微位移值仍可用(0，π/4]训练的模型得出，故只需对(0，π/4]区间内的样本进行训练，得到网络模型。具体关系如表2所示，其中x表示神经网络的直接输出量。

表2 Asinθ|-|Acosθ|、网络输入、输出量的关系

3 BP神经网络结构和算法设计

3.1 BP神经网络

郭雨梅等[9]提出只有一个隐层的三层神经网络,只要隐节点足够多，就可以以任意精度逼近一个非线性函数。故文中选取三层BP神经网络对光栅信号进行精细分。当然隐层节点数并不是越多越好，根据实验误差最小，选取最合适的隐层节点数。

3.2 样本点选取及学习过程

为了消除幅值不稳定性带来的影响，选取[P,S]作为训练样本的输入,P为上一节介绍的分段函数。实际的样本数据由精度较高的光栅位移系统测出。光栅传感器输出的两路互补正弦信号经A/D转换后，判断|Asinθ|-|Acosθ|的正负，确定网络的输入量,再送入神经网络子程序，经过神经网络程序，得出对应1/4周期内的微位移量。每1/4周期对应的区间依次为(0°,90°)、(90°,180°)、(180°,270°)、(270°,360°)，根据分段函数P的对称性，可将(0°,90°)、(90°,180°)、(180°,270°)、(270°,360°)四个区间通过区间(0°,45°)的神经网络模型进行计算。根据系统要求，可确定采用一个输入一个输出的神经网络模型。第1层为输入层；第2层为隐含层，传递函数选取S型“tansig”;第3层为输出层，传递函数选取“purelin”[10-12]。BP神经网络训练过程复杂，耗时时间长，故文中设计将样本数据在MATLAB中运用neff函数创建一个名为net的BP神经网络模型，并运用train函数进行训练，得出各层的权值和阈值。将这些权值和阈值作为初始值存入寄存器，然后再编写神经网络细分子程序进行运算，得出最终细分结果。在编写神经网络子程序时需要用到以下公式：

(5)

(6)

y=f(s2)

(7)

其中，LW1j、bj、IWj1、oj分别为输入层到中间层的权值、中间层各神经元阈值、中间层到输出层的权值、输出层各神经元阈值。

隐含层的传递函数为S型激活函数，输出层的传递函数为线性函数，故得到式8：

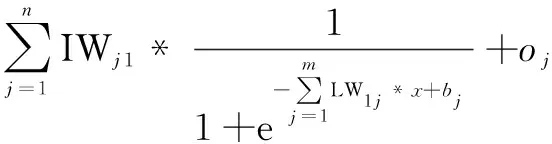
(8)

BP神经网络的隐含层节点数，根据经验可以参照以下公式进行设计。

(9)

其中，h为隐含层节点数；a为输入节点数；b为输出节点数；c为1～10之间的调节常数。由此可知隐含层节点数范围为[2,12]。

不同节点数的网络训练误差如表3所示。

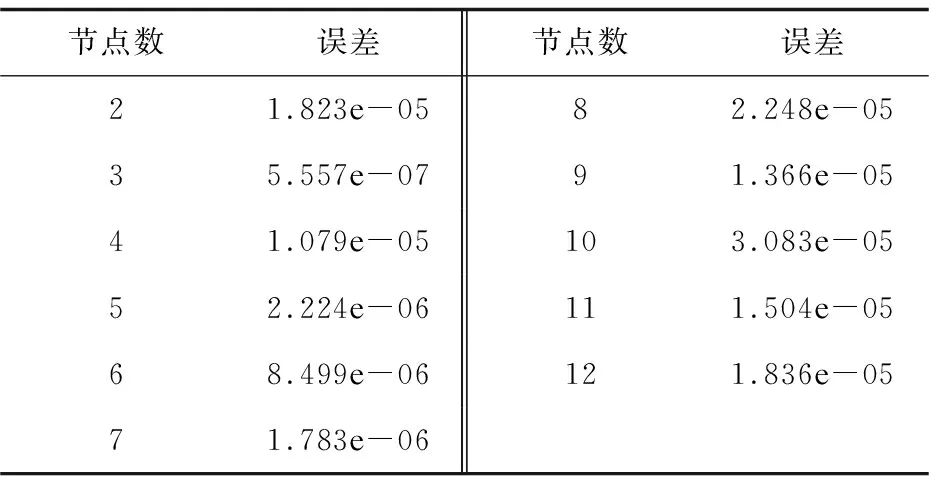
表3 不同节点数的网络训练误差

从表3可以看出，隐含层节点数越多，网络性能并非越好。当隐含层节点数从9增加到12时，误差反而增大。而隐含层节点数为3时误差最小。故选用一个隐层节点数为3的三层网络模型。

4 改进的BP神经网络算法设计

由于BP神经网络算法本身的原因，学习过程可能收敛于局部极小点。而遗传算法是一种自适应全局优化概率搜索算法[13-16]。该算法从很多点开始并行工作，不是局限于一点，故能有效防止搜索过程收敛于局部最优解。前面介绍了网络结构最优的设计，在此基础上，再运用遗传算法的全局搜索能力，搜索到最优的网络权值和阈值。遗传算法主要包括染色体编码与解码，个体适应度的检测评估，选择，交叉，变异等。遗传算法可描述为：

(1)确定种群的大小N为40，交叉概率设为0.7，变异概率设为0.01；根据网络结构，产生N个(LW,IW),通过二进制编码，将(LW,IW)中每一个权值转换成二进制编码，然后组合构成一个完整的染色体。产生N个权值的取值范围为[-20,20],阈值的取值范围为[-10,10]的染色体，将得到由N个染色体构成的初始群体C。

(2)计算出每个个体的适应度fi,再按赌轮盘法进行优质个体的选择，产生新种群。

(3)根据算术交叉方式以及确定的交叉概率，把部分基因进行交换，形成新个体。

(4)通过基因中的某一位变异，可以防止种群陷入超平面，根据设置的变异概率进行变异操作。

(5)重复步骤2～4，直到误差对连续几代种群趋于稳定或不超过某一阈值，则进化计算结束。经过上述方法优化，获得一个接近最优的权值和阈值，再运用BP算法再次寻优，采用梯度下降法，得到网络最优解。

5 硬件设计

该系统硬件主要包括差分放大电路、整形电路、粗细分模块和AD模块。FPGA主要实现四细分、辨向、计数以及神经网络子程序、综合数据处理等功能。

5.1 FPGA选型

文中选用ALTERA公司的Cyclone IV系列芯片，型号为EP4CE6F17C8，是256脚的FBGA封装。这款FPGA可以利用其扩展口直接连接到ADDA模块、摄像头、4.3寸液晶屏、音频模块等等，使用起来极其方便。

5.2 粗细分模块

光栅每移动一个栅距输出一个正弦波。粗细分就是将这一个正弦波分为4段，即四细分。四细分主要是通过辨向与计数的原理来实现的。光栅尺输出的信号，经过前端模拟电路的处理，将得到两路互补的方波信号进行计数，这两路方波信号分别经过两个D触发器，第一个触发器D与第二个触发器D延时一个时钟周期。电平状态按照0010-1011-1101-0100顺序循环变化时，进行加计数操作，即光栅尺正向运动;电平状态按照0001-0111-1110-1000顺序循环变化时，进行减计数操作，即光栅尺反向运动。

5.3 放大器的设计

光栅输出的正弦信号有漂移值，而漂移值会影响精度的提高，故文中设计用两个四运放LM324N对光栅信号进行处理。

5.4 A/D转换模块设计

光栅输出信号经过预处理电路处理(由于篇幅有限，不再详细介绍)，得到两路互补正弦信号U1和U2。AD模块部分采用了两片ADI公司的AD9226将模拟信号转换成12 bit的数字信号，文中运用两片AD芯片能同时对以上两路信号进行处理，减小了AD转换需等待的误差。经过预处理电路后的信号电压变化在-5～5 V之间，而AD9226芯片其电压输入范围为1.0～3.0 V，故文中运用衰减电路来实现上述要求，转换公式为：Vout=1/5Vin+2。AD922的数据转换速率最高为65 MHz，光栅尺的截止频率f=v/w,文中选用的光栅尺速度v不超过120 m/min,栅距为0.02 mm。假设信号周期为100 kHz,根据采样定理，采样频率至少大于200 kHz,实验中采样频率设置为50 MHz,满足设计要求。经过AD转换后得到数字信号，以给FPGA处理。AD采样模块程序运用Verilog HDL语言实现。

5.5 通讯模块设计

将光栅尺最终测得的位移值通过串口通信发送给PC端。硬件设计采用Silicon Labs CP2102GM芯片作为USB和UART电平转换的桥梁,USB接口采用Micro USB接口。引脚RXD接FPGA的M2脚，引脚TXD接FPGA的N1脚，引脚RXD是从PC发送给FPGA的串行数据,引脚TXD是从FPGA发送给PC的串行数据。通讯主要采取串行数据传输方式，消息帧主要由起始位、数据位、校验位等组成。串口发送程序包含3个程序：时钟产生程序clkdiv.v、串口发送程序uarttx.v和串口发送测试程序。这三个程序都是用Verilog HDL语言建模实现的。

6 软件设计

细分系统的硬件设计完成后，还需对其进行软件设计。在Quartus II开发环境下，运用Verilog HDL语言编程。光栅信号经过一系列的硬件电路处理后，由FPGA完成四细分并对AD模块进行采样，通过两个串口分别将计数器的值和采集的值传给上位机，然后由上位机读取串口的数据，判断细分方法的选择，最后得出相应细分方法测得的位移值。FPGA和上位机的软件流程分别如图1和图2所示。

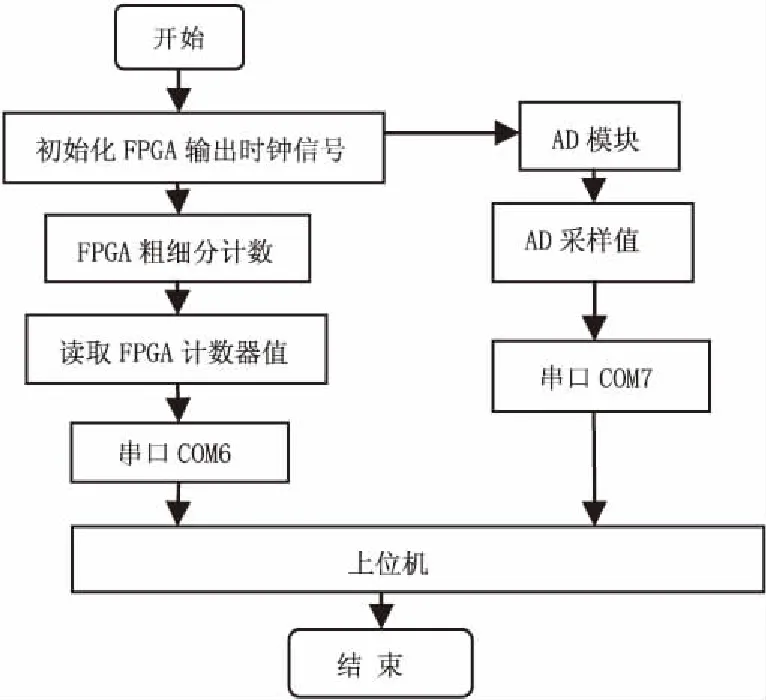
图1 FPGA软件程序流程

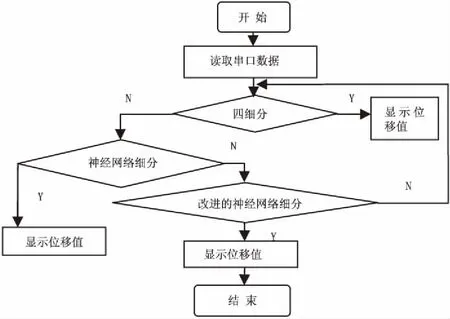
图2 上位机软件程序流程

7 实验结果分析

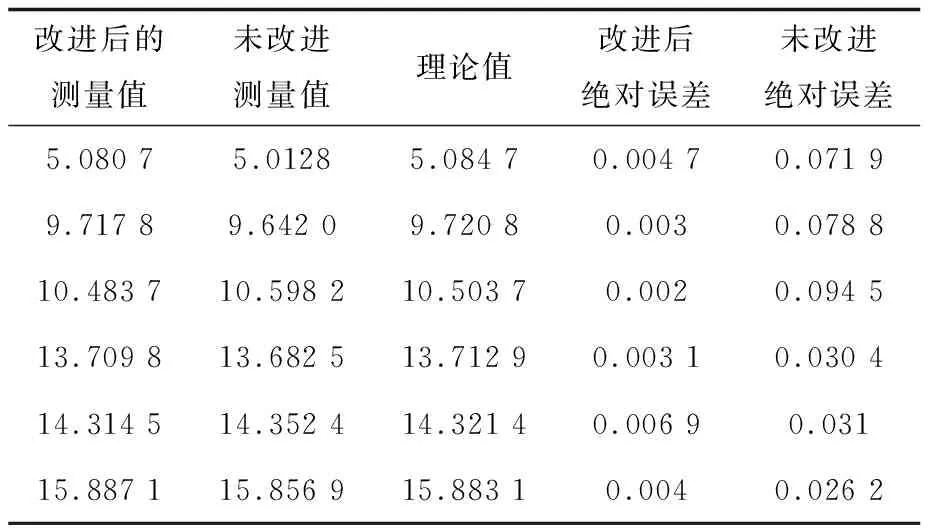
根据上述细分方案，编写上位机测控软件，采集非样本点的数据进行位移理论计算，实验数据如表4所示。从表中可以看出，实际位移值和理论值的绝对误差远小于10-2数量级范围，满足系统要求。改进后的神经网络细分算法测量值的绝对误差比未改进的测量值的绝对误差小，说明改进算法提高了光栅测量的精度，验证了文中细分算法的可行性，提高了系统的稳定性和细分倍数。

表4 理论值与实际值对比

μm

8 结束语

文中详细论述了如何运用软硬件相结合的细分方法(硬件细分采用四细分，软件细分采用BP神经网络细分)来提高光栅的细分倍数，并对神经网络算法进行了改进。通过采集非样本点数据进行测试，验证了该细分方法的可行性，并可简化硬件结构,提高系统的可靠性和抗干扰能力,具有一定的实用价值。该神经网络软件细分技术具有一定的创新性，同时也对硬件实现神经网络细分算法较复杂的问题提供了新的解决途径，但目前只是初步完成了提高细分倍数的目的，还未对光栅测量系统进行优化。未来的研究重点是对其误差进行自动补偿。

参考文献：

[1] 李金艳.基于幅值采样技术的光栅信号细分的研究[D].哈尔滨：哈尔滨理工大学,2013.

[2] 朱维娜.基于DSP2812的光栅细分技术研究[D].成都:西南交通大学，2012.

[3] 胡晓东.基于FPGA与单片机的高精度电子经纬仪光电信号处理系统研制[D].南京：南京理工大学，2004.

[4] 李怀琼,陈 钱,王 钰.新型光栅信号数字细分技术及其误差分析[J].计量学报,2001,22(4)：281-283.

[5] 张金杰.鉴相法光栅位移测量系统的研究[D].沈阳:沈阳工业大学,2008.

[6] 于 耕，马晓梅，郭华鹏．圆光栅测角系统信号细分电路设计[J]．电子设计工程，2012,20(15):99-102.

[7] 金建新．输出正交正弦波的光栅尺在位移测量中的脉冲细分原理[J]．自动化仪表,2002,23(1):17-19.

[8] SANCHEZ-BREA L M,MORLANES T.Metrological errors in optical encoders[J].Measurement Science and Technology,2008,19(11):115104.

[9] 郭雨梅,关 蕊,钟 媛.基于径向基神经网络的光栅细分方法[J].沈阳工业大学学报，2011,33(2):193-197．

[10] 丁 旭,李彬华,杨晓晗.一种基于FPGA的光栅信号细分方法[J].传感技术学报,2016,29(6):846-853.

[11] HU Haijiang, ZHANG Fengdeng. Advanced bidirectional subdivision algorithm for orthogonal fringes in precision optical measurement instruments[J].International Journal for Light and Electron Optics,2012,123(15):1322-1325．

[12] 关 蕊.基于神经网络的莫尔条纹信号细分方法与应用[D].沈阳:沈阳工业大学,2010.

[13] 雷英杰，张善文，李续武,等.遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005.

[14] SUN Q,CHE W G,WANG H L.Bayesian regularization BP neural network model for the stock price prediction[M]//Foundations and applications of intelligent systems.Berlin:Springer,2014:521-531.

[15] GURESEN E,KAYAKUTLU G,DAIM T U.Using artificial neural network models in stock market index prediction[J].Expert Systems with Applications,2011,38(8):10389-10397.

[16] ROVITHAKIS G A,CHALKIADAKIS I,ZERVAKIS M E.High-order neural network structure selection for function approximation applications using genetic algorithms[J].IEEE Transactions on Systems,Man and Cybernetics,2004,34(1):150-158.