面向非平衡类问题的k近邻分类算法

郭华平,周 俊,邬长安,范 明

(1.信阳师范学院 计算机与信息技术学院,河南 信阳 464000; 2.郑州大学 信息工程学院,郑州 450000)(*通信作者电子邮箱hpguo_cm@163.com)

0 引言

非平衡类问题是机器学习与模式识别中的一个重要研究方向[1],其表现为一个类的实例数(多数类或者负类)远多于另一个类(少数类或者正类)的实例数[2]。在一些实际应用中,正确识别少数类实例往往比正确识别多数类实例更具价值,如在信用欺诈检测中,只有少数案例属于欺诈案例,如何正确识别这些欺诈案例更加重要[3]。然而传统分类方法如k近邻、决策树、后馈神经网络、支持向量机等通常试图学习具有高准确率的分类模型,这往往导致学习到的模型不能充分考虑到少数类实例的特征,进而忽略甚至错误分类少数类实例[4]。实际上,针对非平衡类问题,准确率不是一个理想的评价指标,召回率(recall)、g-mean、 f-measure以及AUC(Area Under ROC Curve)等常用于评估算法在非平衡类问题上的性能[5]。

处理非平衡类问题的方法大致可以分为两类[6]:

1)基于数据的方法。通过对训练集重抽样以平衡数据集的分布,进而使学习到的模型更倾向于发现少数类特征。该方法不需要对算法本身作过多调整,只需对数据集进行针对性处理。常用的基于数据的方法可分为两种类型:a)重采样,旨在通过对数据集重新采样以减小类不平衡对分类造成的不利影响,通常分为过抽样、欠抽样和组合抽样三种方法。过抽样通过创建新的少数类样本来平衡训练数据集,如随机过抽样[7]和合成少数类过抽样(Synthetic Minority Over-sampling TEchnique, SMOTE)算法[8]等,其中SMOTE是一种广泛使用的过抽样技术,其在少数类样本及其同类近邻样本的连线上创建新的少数类样本以平衡数据分布。欠抽样通过移除一些多数类样本以平衡训练数据集,如随机欠抽样、EasyEnsamble[9]等。组合抽样则是二者的组合[10]。b)数据空间加权，旨在通过利用误分类代价信息来调整训练集分布。Wang等[11]基于此使用非对称误分类代价矩阵提出了一种基于SVM的组合分类方法。

2)基于算法的方法。通过调整已有算法的学习过程以增强分类器识别少数类的能力。该方法需要对算法本身及其应用领域有深刻的理解,并了解其在不平类问题上适应性差的原因。常用的方法包括使用核变换以增强分类器的区分能力[12],将训练目标转换为倾向于正确分类少数类实例的目标函数[13]等。

针对非平衡类问题,本文提出一种基于划分的k近邻(Partition-basedk-Nearest Neighbor, PkNN)算法以提高k近邻模型在少数类上的性能，它是一种特殊的基于数据的非平衡类学习算法。在学习阶段,PkNN使用划分算法(如K-Means、层次聚类等)划分多数类数据集为多个簇,然后将少数类数据集分别与每个簇合并构成一组新的训练数据集,在每个新的训练集上训练一个k近邻模型,因此,该方法构造了一个包含多个k近邻模型的分类器库。之所以这样做的原因是:划分后,在合并的数据集上,多数类和少数类实例的分布更加均衡,如图1所示。在预测阶段,使用划分算法K均值(K-Means)算法、层次聚类(Hierarchical Clustering, HC)等从分类器库中选择一个模型用于预测待分类样本的类别。另外,为了提高模型性能,将SMOTE应用到PkNN的学习过程中。KEEL数据集[14]上的实验结果表明,PkNN能有效提高k近邻分类方法在评价指标recall、g-mean、 f-measure和AUC上的性能;同时,过抽样能进一步提高k近邻的泛化能力,并明显优于其他高级算法。

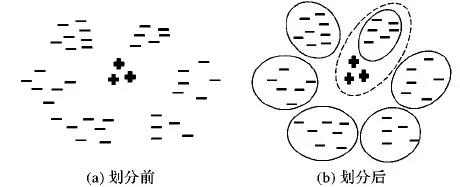
图1 多数类数据集划分前后数据的特征

1 面向非平衡类的k近邻分类算法

1.1 PkNN算法流程与伪码

图2给出了PkNN模型学习和预测过程示意图。在学习(训练)阶段,PkNN首先处理数据集,采用划分算法(如K-Means)将多数类数据集Dmaj划分为m个簇{Ci|i=1, 2,…,m}使得∪Ci=Dmaj,Ci∩Cj=∅,i≠j;然后,PkNN将少数类数据集Dmin分别与每个簇Ci合并得到一个新的训练集Cnew,i=Dmin∪Ci,并在Cnew,i上学习一个k近邻分类模型kNNi。因此PkNN学习了一个包含m个k近邻模型的分类器库。在预测阶段,PkNN使用学习阶段学习的划分模型从分类器库中选择模型预测未知类标号样本x的类别。

算法1给出了PkNN算法伪代码。在训练阶段,PkNN首先将训练数据集分离为多数类和少数类两部分(第1)行),并将多数类数据集划分为m个簇(第2)行);然后,PkNN将每个簇和少数类数据集合并得到一个新的训练集,用于训练一个k近邻模型(第3)～6)行)。在预测阶段,PkNN使用划分阶段学习的划分方法将待预测样本x映射到相应的簇(第7)行),使用相应的k近邻模型预测x的类标号(第8)行)。

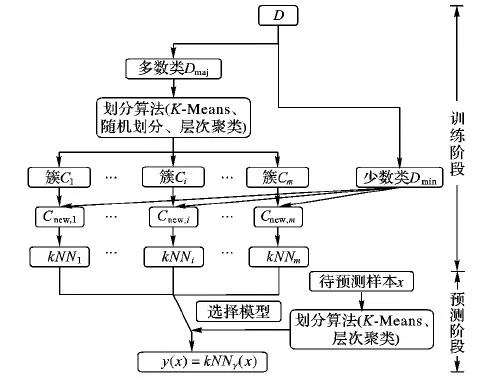
图2 PkNN模型学习和预测过程示意图

算法1 PkNN算法。

训练阶段:

输入 训练集D;划分的簇数目m。

输出 预测模型PkNN。

1) 设Dmaj和Dmin分别为D中的多数类和少数类集合;

2)C=Partition(Dmaj,m);

//划分Dmaj为m个簇,即:C={Ci|i=1, 2,…,m}

3) forCiinCdo

4)Cnew,i=Ci∪Dmin;

5)kNNi= Learner(Cnew,i);

6) end for

预测阶段:

输入 待分类样本x;kNN模型近邻数k。

输出 样本x所属类别y。

7)γ=Partition(x);

//取得x所属的簇标号;

8)y=kNNγ(x,k)

//在相应kNN模型中预测x的类别;

returny

算法1中值得注意的是如何选择划分方法(第2)行和第7)行)。本文分别采用K-Means算法、随机划分法以及层次聚类方法划分多数类数据集。

1.2 基于K-Means数据划分法

K-Means算法是一种经典的聚类算法,因其简单、适应性强的特点,广泛应用于多种实际问题当中[15]。该算法是一种基于平方误差的聚类算法[16],对于给定的样本集D={x1,x2, …,xn},算法的最终目标是学习到的簇C={C1,C2, …,Cm}具有最小化平方误差,形式化地:

(1)

其中:

(2)

μj为簇Cj簇心(均值向量);|Cj|为簇Cj中样本的个数。直观地看,式(1)在一定程度上刻画了簇内样本围绕簇心的紧密程度,值越小则簇内样本相似度越高。

K-Means采用迭代方法来近似优化式(1),具体过程如下:1)从D中任选m个样本作为初始簇心{μ1,μ2,…,μm};2)对于每个样本xi∈D,计算其与各簇心μj(1≤j≤m)的距离dij=‖xi-μj‖,并将xi归并到具有最小距离diλ对应的簇Cλ中,即Cλ=Cλ∪ {xi};3)重复过程2)直到D中所有样本都处理完毕;4)利用式(2)更新每个簇的簇心,若μj′≠μj则更新簇心μj为μj′,否则保持簇心不变;5)重复步骤2)～4),直至所有簇的簇心都不再变化。

本文算法PkNN将K-Means算法应用到多数类样本集的划分过程中(参见算法1第2)行),并使用欧氏距离计算样本与簇心间的距离,形式化地

(3)

同样地,在预测阶段,PkNN使用欧氏距离(式(3))预测样本x所属簇的标号γ(参见算法1第7)行),即

(4)

然后使用相应的模型kNNγ预测待测样本x的类标号。

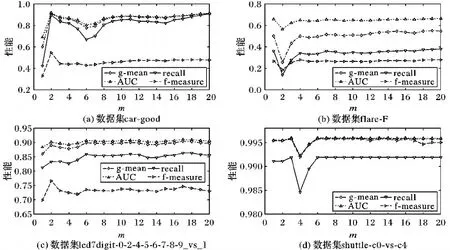
图3 KM-kNN在四个数据集上的性能与m取值的关系

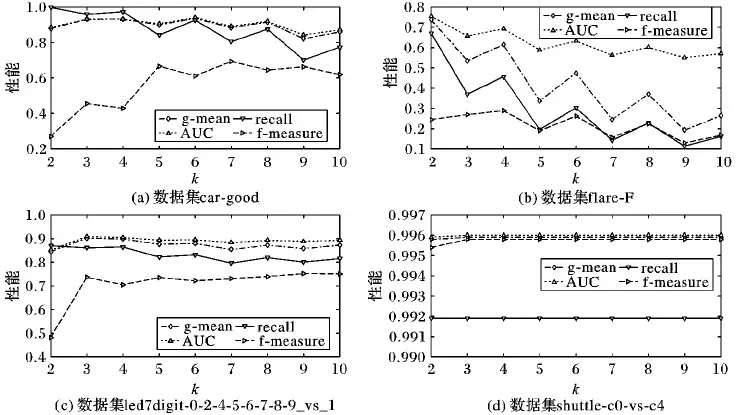
图4 KM-kNN在四个数据集上的性能与k取值的关系

1.3 随机数据划分法

随机划分法是最简单的一种数据划分方法,其将任意一个多数类样本随机地划分到某一个簇中,即对于每一个样本x∈Dmaj,在区间[1,m]内随机对x赋以一个簇标号λ,再x将并入相应的簇Cλ=Cλ∪{x}中,即可完成对Dmaj的随机划分。

本文算法PkNN将随机划分方法应用到多数类数据集的划分过程中(参见算法1第2)行)。为了算法预测方便,本文使用式(2)计算每个划分的中心。在预测阶段,PkNN使用式(3)(欧氏距离)和式(4)获得样本x距离最近的簇的簇标号γ(参见算法1第7)行),然后采用相应的预测模型kNNγ预测样本x所属的类别。

1.4 基于层次聚类数据划分法

层次聚类(Hierarchical Clustering, HC)也是一种广泛使用的聚类算法,其在不同的层次对数据集进行聚类,从而形成树形的聚类结构[17]。本文算法PkNN采用自下而上凝聚策略的层次聚类划分多数类数据集:首先将数据集中每一个样本看作一个初始簇,然后在算法运行的每一步中找出距离最近的两个簇进行合并,不断重复该过程,直至达到预设的簇个数。PkNN采用簇间最小距离来度量两个簇之间的距离,形式化地:

d(Ci,Cj)=

其中dist(x,z)为样本x和z的欧氏距离。与随机数据划分法类似,为了算法预测方便,本文使用式(2)计算每个簇的中心。在预测阶段,PkNN使用式(3)(欧氏距离)计算待预测样本x与簇心的距离,根据最近距离确定x所属的簇标号γ,然后采用相应的预测模型kNNγ预测样本x所属的类别。

2 参数学习

在算法1中,需要注意两个输入参数,即划分多数类数据集的簇数m和kNN的近邻数k。本章使用K-Means算法作为划分方法讨论这两个参数。

图3展示了在四个数据集上m(簇数)对模型性能的影响，其中KM-kNN表示使用K-Means对数据进行划分，然后直接在划分后的数据集上学习k近邻模型(参考3.1节)。图3结果获得方式:在数据集上执行10次10折交叉验证,并将模型性能的平均值作为最终输出结果。这里设置近邻数k=3。

从图3可以看出,划分方法能有效提高k近邻模型在非平衡类问题上的性能(m=1表示直接在未划分的实例集上学习k近邻模型)。另外,通过观察图3可以发现当m=「Nmaj/Nmin×2⎤(Nmaj和Nmin分别表示数据集多数类与少数类样本的个数)时,模型在四个数据集上均取得较好的分类性能。该结果与期望结果m=Nmaj/Nmin(每个簇的样本数与少数类样本数比例为1∶1)并不一致,其原因是:划分算法不能保证各个簇大小相当,其中一些小簇样本数可能远小于少数类样本数,这会降低模型的性能。故在后面的实验中,本文取其划分的簇数为m=「Nmaj/Nmin×2⎤。

图4展示了在四个数据集上k(近邻数)对模型在recall、g-mean、 f-measure和AUC性能上的影响。图4所有的结果获得方法与图3一致。从图4可看出，当k取值为3时,四个模型的分类性能均可达到较优的效果,故本文取定k=3,并将其应用到后续的实验中。

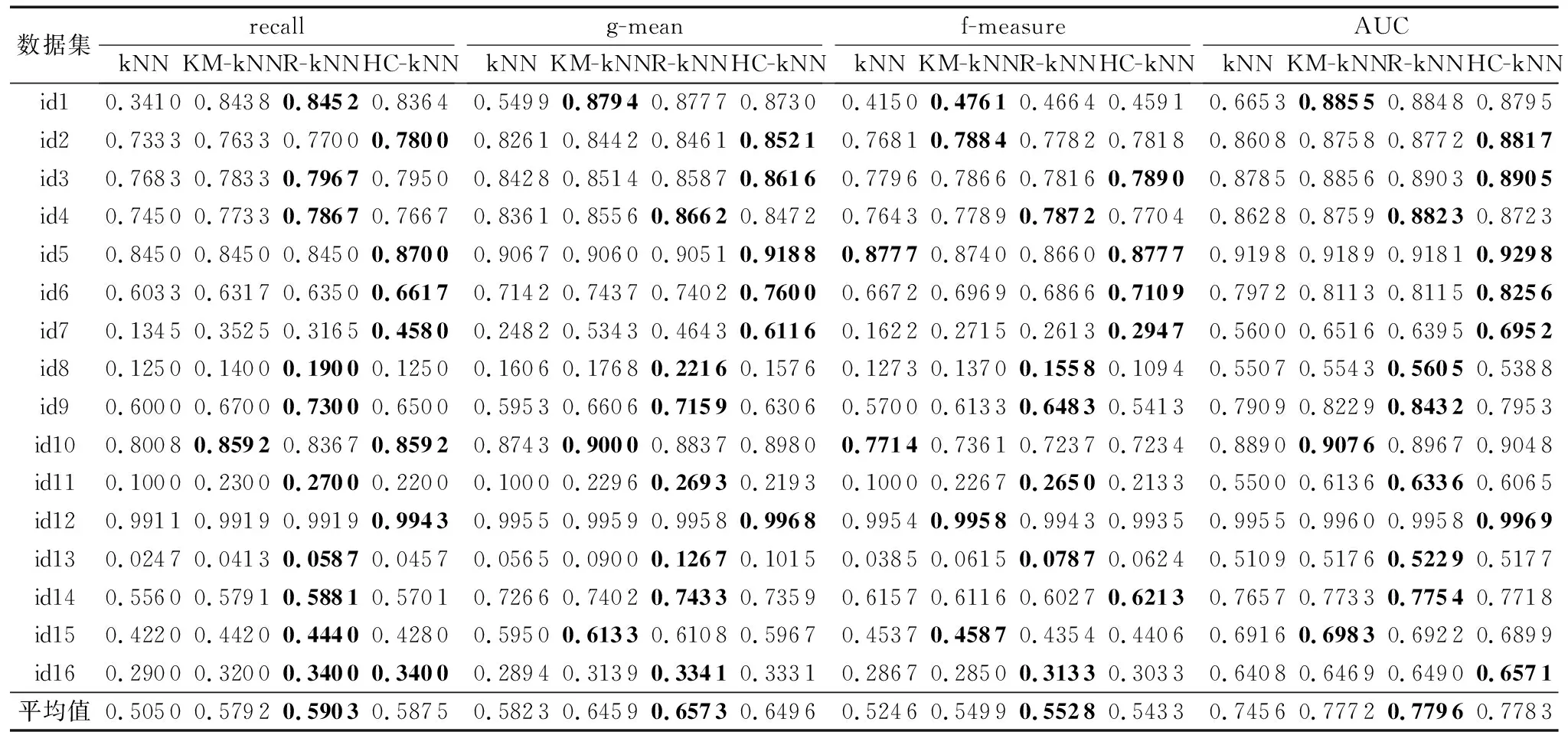
表2 kNN、KM-kNN、R-kNN和HC-kNN在recall、g-mean、 f-measure和AUC上性能比较

注:性能最优的结果加粗表示。

表1 实验数据集

3 实验

3.1 数据集和实验设置

本文从KEEL机器学习数据库中随机选取16个非平类数据集进行实验,数据集的相关描述如表1所示,其中Exs、Atts和IR分别表示数据集的实例个数、属性个数和不平衡度(多数类与少数类实例数目的比例)。对于每个数据集,采用10次10折交叉验证来测试模型的分类性能,因此,在每个数据集合上实际共计构建了100个模型。

为评估本文提出的面向非平衡类问题的k近邻分类算法的分类性能,本文设计了两组实验:

1)PkNN的三种具体实现模型KM-kNN、R-kNN和HC-kNN与传统的kNN模型相比较：KM-kNN表示基于K-Means数据划分法的k近邻分类算法；R-kNN表示基于随机数据划分法的k近邻分类算法；HC-kNN表示基于层次聚类的k近邻分类算法。

2)将过抽样技术SMOTE应用到PkNN中,检测抽样技术对PkNN的影响,选择KM-kNN作为PkNN算法的代表。

过抽样技术设置划分簇数m=「Nmaj/Nmin×2⎤,k近邻中的近邻数k=3,其中Nmaj和Nmin分别表示多数类和少数类实例数(参见第2章)。

3.2 PkNN的性能

为评估本文算法的分类性能,把提出的面向不平衡类问题的k近邻分类方法的三种具体模型(即KM-kNN、R-kNN和HC-kNN)与kNN算法进行比较。

表2显示了模型分别在评估指标recall、g-mean、 f-measure和AUC上的性能。从表2可看出：本文提出的面向非平衡类问题的分类算法的三种具体模型各项指标平均值良好，且相差不大。传统kNN算法仅在f-measure指标中有一次在id10中是最优的(id5中与HC-kNN并列最优)，所有指标中的平均值均最差。该实验结果表明,本文算法能很好地适应不平衡类环境,有效地提高了模型识别少数类样本的能力。本文算法对模型分类性能影响的关键因素是对数据集进行划分,而非具体某种划分方法。

3.3 抽样技术对PkNN的影响

为了检测抽样技术对PkNN的影响,本文将KM-kNN与SMOTE相结合,并比较算法KM-kNN、SM-kNN和SM-KM-kNN的性能:

1)KM-kNN(K-Means+kNN)为表示基于K-Means数据划分法的k近邻分类算法(参考3.1节)。

2)SM-kNN(SMOTE+kNN)为使用SMOTE直接预处理原始训练数据集,然后在处理过的数据集上学习k近邻模型。

3)SM-KM-kNN(SMOTE+KM-kNN)为KM-kNN在学习每个k近邻模型前,使用SMOTE过抽样方法处理新创建的训练数据集(算法1第4)行和第5)行之间),然后学习k近邻模型。

表3给出了KM-kNN、SM-kNN和SM-KM-kNN在recall、g-mean、 f-measure和AUC上的性能。从表3可以看出：本文提出的PkNN算法(以KM-kNN为例)与SM-kNN性能相当；而SM-KM-kNN的分类性能明显优于前两者,各项指标的平均值均最优。

该结果表明:1)划分方法与抽样技术对kNN性能提升效果相当;2)SMOTE抽样技术能显著提升PkNN的性能;3)将抽样技术和划分方法有效地结合能更好地提升k近邻在非平衡类问题上的性能。

注:性能最优的结果加粗表示。

4 结语

本文提出一种基于划分的面向非平衡类问题的k近邻分类算法。与传统的k近邻方法不同,在学习阶段,该算法使用划分方法将多数类数据集划分为多个簇,将每个簇与少数类数据集合并构建新的相对平衡的训练集集合;然后在集合的每个成员上训练一个k近邻模型,进而获得k近邻模型库。在预测阶段,使用学习到的划分方法选择库中的模型预测样本类标号。另外,还将过抽样技术SMOTE应用到该算法中,以进一步提高该算法的性能。相关实验结果表明:1)本文算法能显著提升k近邻在非平衡类问题上的泛化能力;2)基于划分的方法与基于SMOTE的过抽样技术在处理非平衡问题上的能力相当(针对k近邻算法);3)SMOTE能进一步提升基于划分的k近邻算法在非平衡类问题上的泛化能力。

参考文献(References)

[1] GUO H, LI Y, SHANG J, et al. Learning from class-imbalanced data: review of methods and applications [J]. Expert Systems with Applications, 2017, 73: 220-239.

[2] LIN W, TSAI C, HU Y, et al. Clustering-based undersampling in class-imbalanced data [J]. Information Sciences, 2017, 409: 17-26.

[3] SANZ J, BERNARDO A D, HERRERA F, et al. A compact evolutionary interval-valued fuzzy rule-based classification system for the modeling and prediction of real-world financial applications with imbalanced data [J]. IEEE Transactions on Fuzzy Systems, 2015, 23(4): 973-990.

[4] CHAWLA N, JAKOWICZ V N, KOTCZ A. Editorial: special issue on learning from imbalanced data sets [J]. ACM Special Interest Group on Knowledge Discovery and Data Mining Explorations, 2004, 6(1): 1-6.

[5] 郭华平, 董亚东, 毛海涛, 等. 一种基于逻辑判别式的稀有类分类方法[J]. 小型微型计算机系统, 2016, 37(1): 140-145.(GUO H P, DONG Y D, MAO H T, et al. Logistic discrimination based rare-class classification method[J]. Journal of Chinese Computer Systems, 2016, 37(1): 140-145.)

[6] SUN Y, WONG A K C, KAMEL M S. Classification of imbalanced data: a review [J]. International Journal of Pattern Recognition and Artificial Intelligence, 2009, 23(4): 687-719.

[7] TAHIR M A, KITTLER J, MIKOLAJCZYK K, et al. A multiple expert approach to the class imbalance problem using inverse random under sampling [C]// Proceedings of 8th International Workshop on Multiple Classifier Systems. Berlin: Springer, 2009: 82-91.

[8] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique [J]. Journal of Artificial Intelligence Research, 2002, 16: 321-357.

[9] LIU X, WU J, ZHOU Z. Exploratory undersampling for class-imbalance learning [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 2009, 39(2): 539-550.

[10] LI P, QIAO P, LIU Y. A hybrid re-sampling method for SVM learning from imbalanced data sets [C]// FSKD 2008: Proceedings of the Fifth International Conference on Fuzzy Systems and Knowledge Discovery. Washington, DC: IEEE Computer Society,2008: 65-69.

[11] WANG B X, JAPKOWICZ N. Boosting support vector machines for imbalanced data sets [J]. Knowledge and Information Systems, 2010, 25(1): 1-20.

[12] ZHANG Y, FU P, LIU W, et al. Imbalanced data classification based on scaling kernel-based support vector machine [J]. Neural Computing and Applications, 2014, 25(3/4): 927-935.

[13] GUO H, LIU H, WU C, et al. Logistic discrimination based on G-mean and F-measure for imbalanced problem [J]. Journal of Intelligent and Fuzzy Systems, 2016, 31(3): 1155-1166.

[14] ALCALA-FDEZ J, FERNANDEZ A, LUENGO J, et al. KEEL data-mining software tool: data set repository, integration of algorithms and experimental analysis framework [J]. Journal of Multiple-Valued Logic and Soft Computing, 2011, 17(2/3): 255-287.

[15] OLIVEIRA G V, COUTINHO F P, CAMPELLO R J G B, et al. Improvingk-means through distributed scalable metaheuristics [J]. Neurocomputing, 2017, 246: 45-57.

[16] BERKHIN P. A survey of clustering data mining techniques [J]. Grouping Multidimensional Data, 2006, 43(1): 25-71.

[17] RUI XU, DONALD C. WUNSCH II. Survey of clustering algorithms[J]. IEEE Transactions on Neural Networks, 2005, 16(3): 645-678.