附件机匣振动力学行为及寿命分析

殷 缘 ，杨 劢 ，信 琦 ，陈云霞

（1.北京航空航天大学可靠性与系统工程学院，北京100191；2.中国船舶工业系统研究院，北京100094；3.中国航发沈阳发动机研究所，沈阳110015）

0 引言

航空发动机附件机匣是航空发动机的重要部件，对其力学行为和寿命进行分析以获得可靠性和寿命指标结果至关重要。附件机匣在工作时，不仅受到轴承载荷、自身和安装附件重力的影响，同时由于齿轮系统高速转动产热以及喷油散热使得其始终处于较复杂的温度场中[1]，且由于附件机匣内部齿轮系统啮合传动以及在安装、运行过程中的误差和故障等因素导致其处于复杂的振动环境中[2]。考虑到附件机匣工作环境的复杂多样性，以及同时承受机械载荷、振动载荷以及热载荷，李锦花等结合MASTA软件和ANSYS软件计算同时受到轴承载荷和传动附件安装弯矩影响下壳体的变形[3]；郭梅等将轮齿啮合时变刚度和静传递误差产生的啮合力作为系统振动激励，采用有限元方法分析附件机匣系统的振动响应[4]；吴鸿等采用有限元方法建立附件机匣壳体稳态热分析模型，给出壳体的温度场分布[5]。然而，上述研究仅包含机械载荷、振动或者温度场中的某一方面，不能全面反映其在复杂工作环境和热固条件下的振动载荷情况。热、固、振载荷会影响附件机匣应力分布等力学行为，从而影响其疲劳寿命。因此，在热、固、振条件共同作用下进行附件机匣的力学行为以及寿命建模分析是十分重要的。

本文基于有限元软件ANSYS Workbench，同时考虑附件机匣壳体自身重力和固定约束条件、轴承载荷、温度场以及振动载荷作用，在不同工况下进行附件机匣壳体力学行为分析，计算得到附件机匣应力响应PSD谱，并根据应力响应PSD谱采用雨流循环计数方法对附件机匣寿命指标进行估计。

1 力学行为建模及分析

在热、固、振多载荷耦合作用下，运用ANSYS Workbench对其力学行为进行建模及分析。

1.1 模型定义、边界以及输入条件

1.1.1 模型定义

在实际工作环境中，各种负载悬挂在附件机匣两侧，对其力学行为分析产生影响。因此，在CAD模型上添加质点块(point mass)来定义负载对附件机匣的惯性影响，如图1所示。

图1 模型定义

图1定义模型中各负载的质量以及在局部坐标系中的位置见表1。

1.1.2 边界条件

进行ANSYS有限元仿真时，边界条件指运动边界上方程组的解应该满足的条件。针对附件机匣的边界条件为吊耳处固定约束。

表1 负载附件的质量以及坐标

1.1.3 输入条件

进行附件机匣热、固、振耦合作用下的力学行为分析，涉及机械载荷、振动载荷和热，因此输入条件有：机匣重力、温度场、轴承载荷、PSD谱。

根据ANSYS FLUENT产热分析，得到附件机匣壳体上各部位温度，并采用EXCEL拟合得到附件机匣温度分布函数。环境温度设置为90℃，在附件机匣中部建立局部坐标系，以该坐标系为基准添加温度，温度变化图线如图2所示。

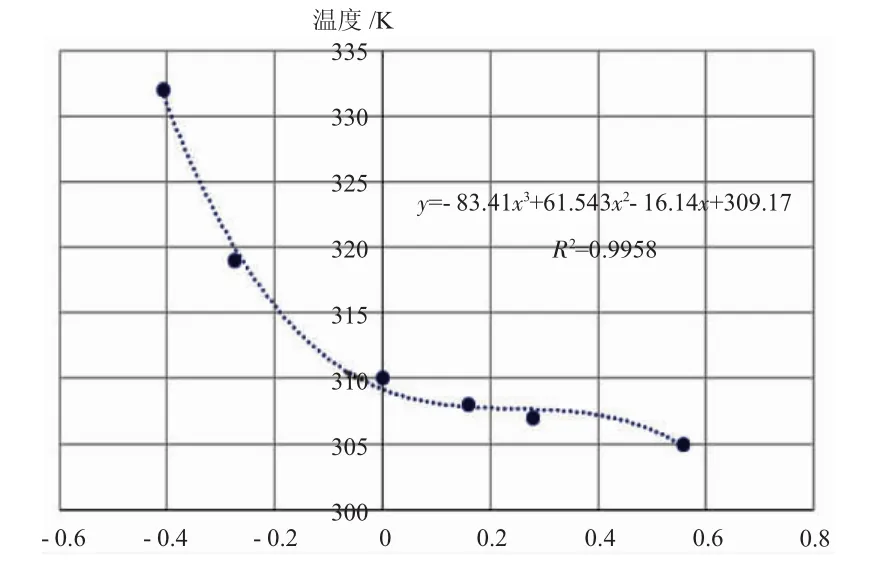
图2 附件机匣不同部位的温度

因此，温度变化函数为

式中：x为附件机匣与坐标原点的相对位置；y为该部位的温度值。

图3 附件机匣温度场

加载温度场到附件机匣上，如图3所示。附件机匣内部共有10个齿轮轴，每个轴两端各有1个轴承，仅承受径向力。采用LMS Virtual Lab.Motion进行整体仿真，选取每个轴承的最大径向力并加载到附件机匣上，具体数值见表2。

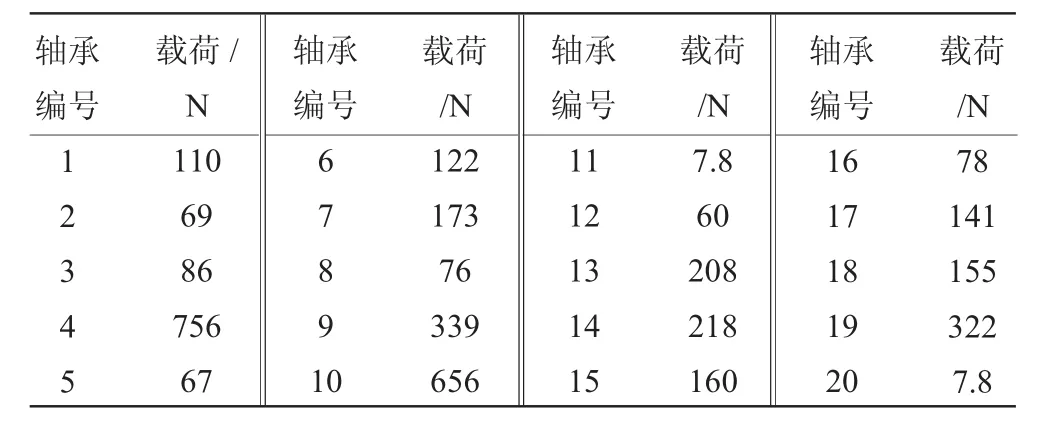
表2 轴承载荷

随机振动输入的加度素功率谱频率范围为0～2000 Hz，各频段振动量值见表3。

表3 该工况下每频段振动量值

1.2 网格划分

附件机匣壳体几何机构较为复杂，建议采用快速自动生成的四面体网格进行划分。此外，在划分网格时选择合适的网格大小对求解的精度以及求解速度十分重要。

结合附件机匣实际尺寸，使用全局8 mm、全局16 mm、附件机匣两侧(平板处)32 mm其余8 mm、两侧16 mm其余8 mm 4种尺寸划分网格，结果见表4。

表4 网格划分结果相关参数

其中，畸变度(skewness)为网格质量的重要参数，指单元相对其理想形状的相对扭曲的度量，是1个值在0(极好的)到1(无法接受的)之间的比例因子。根据表4可知，不同网格尺寸得到的畸变度最大值和平均值基本接近；节点数和单元数为尺寸8 mm的最少，选择较少节点和单元的尺寸可以提高运算速度。

对于8 mm所得的单元和节点数比16 mm得到的少，其原因在于8 mm时的平滑参数(transition)设置为fast，而16 mm设置为slow。若8 mm网格尺寸设置为slow则会输出过多单元，导致计算量太大而不能进行模态分析；若16 mm设置为fast则网格质量太低不足以比较。而网格尺寸为8 mm时畸变度为0.95的单元所占比例最小，因此8 mm的网格尺寸最理想，其对应的机匣局部网格划分结果如图4所示。

图4 附件机匣网格

1.3 预应力模态分析

模态分析用来计算结构的振动特性，包括固有频率和振型。由于ANSYS随机振动分析采用模态叠加法，因此随机振动分析前必须进行模态分析。本文中静力学分析设置的边界和输入条件使结构中存在预应力，会导致结构刚度变化进而影响模态分析及后续振动分析结果。因此，在进行预应力模态分析时需考虑机匣载荷和温度对结构刚度的影响。

设置PSD谱最高频率为2000 Hz，进行15阶模态分析，固有频率结果皆小于500 Hz。因此，为保证响应结果的精确性分析，在前45阶模态中，第1、6、15、45阶固有频率结果见表5。

1.4 随机振动响应输出

根据仿真计算的薄弱位置的应力响应PSD谱进行寿命分析。根据随机振动理论，响应PSD谱可以由单自由度系统的传递函数H（ω）根据输入（激励）PSD谱通过模态叠加方法计算得到。第i个自由度的响应PSD谱由以下3部分组成：

动态部分

拟静态部分

协方差部分

式中：n为振型数；r1、r2分别为节点数和基础PSD谱数。

单自由度的传递函数根据不同的输入PSD谱和响应类型有不同形式。本文中输入为加速度PSD谱，输出为应力PSD谱，其传递函数形式为

式中：ω为外激励频率；ωj为第j阶模态的自然圆弧频率。

采用ANSYS Workbench得到最大等效应力结果见表6。

表6 最大等效应力计算结果

从表6中可知，振动谱沿Z轴方向等效应力最大，如图5所示。

图5 等效应力

从图中可见附件机匣壳体的应力最大点（即薄弱位置），从而能够输出薄弱位置的正应力σx、σy、σz和剪应力 τxy、τyz、τzz的响应 PSD 谱。

应力响应PSD谱如图6（a）所示。已知功率谱密度值-频率值关系曲线下面积的开方即为均方根值（RMS）[6]。从图 6（a）中可见，σx响应 PSD谱的 RMS皆远大于其余应力，并且各应力频率主要集中于90～150 Hz，将该频率区间图像放大，如如图 6（b）所示，发现σz和σyz的RMS远小于其余应力。

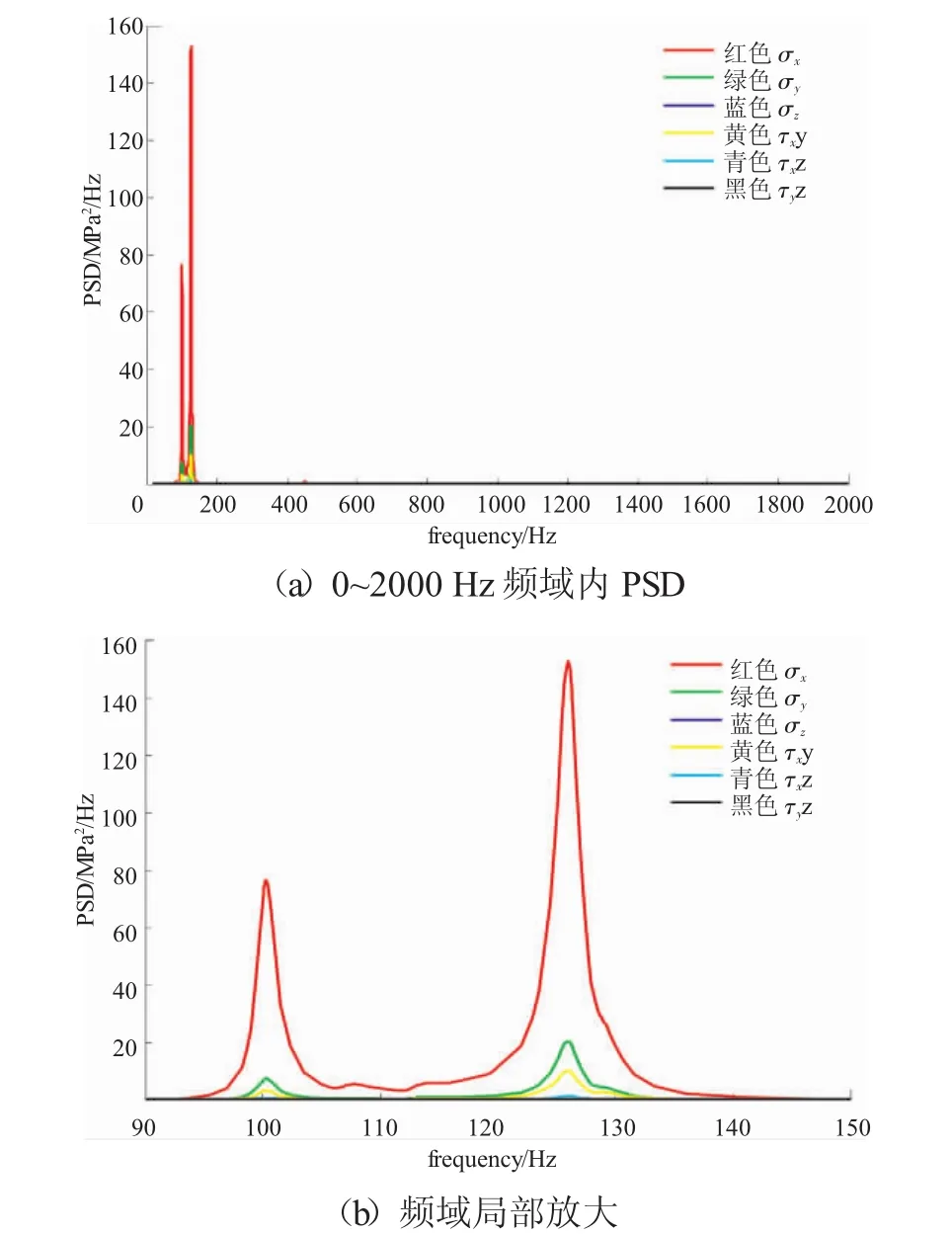
图6 应力响应PSD谱

2 寿命建模及分析

2.1 雨流循环计数方法

根据第1.4节输出的响应PSD谱，采用雨流循环计数法（RFC）计算寿命。RFC是循环计数法的1种。循环技术法指在已知峰值概率密度函数的情况下，对应力峰值进行循环计数得到幅值信息，然后进行寿命计算。常用的循环计数法还有变程计数法（RC）和水平穿越计数法（NB）[7]。

雨流计数法是公认最好的疲劳损伤估计方法，但其计算过程比较繁琐，准确解析式很难给出[8-9]。然而，在任意平稳高斯过程中，线性损伤准则有效的情况下，雨流计数损伤总是处于2种损伤值之间[10-11]

式中为雨流计数损伤；DRC为变程计数损伤；DNB为水平穿越计数损伤。

从式（6）中可知，估计雨流计数损伤可以通过在其上下界中找到1个合适的中间点。因此，D.Benasciutti和R.Tovo提出雨流计数损伤可以由和加权线性组合得到[12]

变程计数法和水平穿越计数法[13]计算疲劳损伤的近似公式为

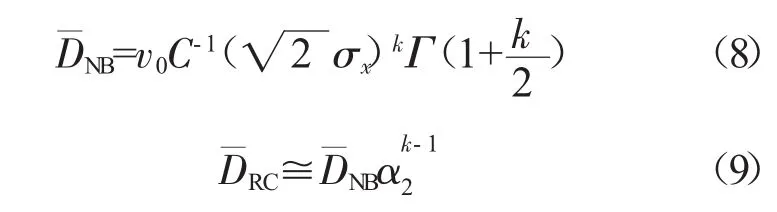
式中：υ0为谱密度函数Sx（ω）的平均上跨率

式中：λm为单边谱密度函数Sx（ω）的谱距

方差由 λ0决定

C和k为S-N曲线中的参数

权重b的选择取决于响应的谱密度函数。D.Benasciutti和R.Tovo给出b的表达式为

其中

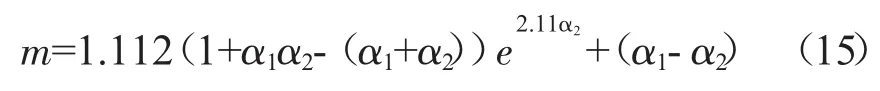
对于谱密度函数 Sx（ω），α1/α2为其带宽参数，取值为[0,1][14]。

2.2 线性疲劳累计损伤理论

根据线性疲劳累积损伤理论，计算附件机匣的总损伤量从而给出其疲劳寿命[15]。

式中：D为总损伤量；Di为单个循环造成的损伤。

线性疲劳累计损伤理论假定损伤量D=1时试件将发生疲劳破坏。因此，疲劳寿命为

2.3 疲劳寿命计算

根据得到的响应PSD谱（图6），运用雨流循环计数法并采用MATLAB编程计算附件机匣的疲劳寿命。由于σx响应PSD谱RMS远大于其余应力，根据σx响应PSD谱计算附件机匣的损伤以及疲劳寿命，结果见表7。

根据6个应力的响应PSD谱计算其单位时间内的损伤，再叠加计算所有功率谱造成的单位时间损伤，从而得到附件机匣总损伤以及寿命结果，见表8。

表7 损伤及疲劳寿命计算结果

从表7、8中可知，2种计算方式的结果非常接近，表明 RMS非常小的 σy、σz，τxy、τyz、τzz对附件机匣的损伤以及寿命计算结果影响很小。

3 结论

本文综合考虑附件机匣复杂的工作环境，包括自身重力和固定约束条件、轴承载荷、温度场以及振动载荷，分析计算附件机匣壳体在机械载荷、温度并施加随机振动谱得到的应力响应PSD谱，结合雨流循环计数方法计算附件机匣壳体的疲劳寿命。在寿命计算时，对比单独采用RMS最大的应力PSD谱和采用所有应力PSD谱计算得到的寿命结果分别为3.25828×106min和3.25823×106min，相差仅为50 min。因此，可以选用RMS最大的PSD谱计算附件机匣的疲劳寿命。

[1]吕亚国，刘振侠，路彬，等.航空发动机附件机匣热分析研究[J].润滑与密封,2011,36（10）：62-80.LU Yaguo,LIU Zhenxia,LU Bin,et al.Thermal analysis of aeroengine accessory gearbox[J].Lubrication Engineering,2011，36（10）：62-80.(in Chinese)

[2]王桂华，刘海年.航空发动机成附件振动环境试验剖面确定方法研究[J].推进技术，2013，34（8）：1101-1107.WANG Guihua,LIU Hainian.Study on formulating method for vibration environment test profiles of aeroengine accessories[J].Journal of Propulsion Technology，2013，34（8）：1101-1107.(in Chinese)

[3]李锦花，史妍妍，张茂强，等.航空发动机附件机匣壳体变形分析[J].航空发动机，2013，39（3）：59-72.LI Jinhua,SHI Yanyan,ZHANG Maoqiang,et al.Analysis of accessory gearbox housing distortion for aeroengine[J].Aeroengine，2013，39（3）：59-72.(in Chinese)

[4]郭梅，陈聪慧，王建军，等.发动机附件机匣结构系统振动特性[J].航空动力学报，2013，28（7）：1607-1612.GUO Mei,CHEN Chonghui,WANG Jianjun.Vibration characteristics of accessory gearbox structure system of engine [J].Journal of Aerospace Power，2013，28（7）：1607-1612.(in Chinese)

[5]吴鸿，李国权，齐乐华.基于ANSYS的附件机匣抽油口润滑油温度计算[J].航空发动机，2006，32（3）：31-35.WU Hong,LI Guoquan,QI Lehua.Lubrication temperature calculation of the oil outlet for accessory gearbox based on ANSYS[J].Aeroengine，2006，32（3）：31-35.(in Chinese)

[6]郑志国，王宇峰.随机振动中的参数介绍及计算方法[J].电子产品可靠性与环境试验，2009，26（7）：45-48.ZHENG Zhiguo,WANG Yufeng.Introduction of parameters in random vibration and their calculation[J].Electronic Product Reliability and Environmental Testing，2009，26（7）：45-48.(in Chinese)

[7]王明珠.结构疲劳振动寿命分析方法研究[D].南京:南京航空航天大学,2009.WANG Mingzhu.Research on life analysis method for structure vibration fatigue[D].Nanjing：Nanjing University of Aeronautics and Astronautics,2009.

[8]Petrucci G，Zuccarello B.On the estimation of the fatigue cycle distribution from spectral density data [J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science，1999，213（8）：819-831.

[9]Petrucci G,Di Paola M,Zuccarello B.On the characterization of dynamic properties of random processes by spectral parameters[J].Journal of Applied Mechanics，2000，67（3）：519-526.

[10]Rychlik I.Note on cycle counts in irregular loads[J].Fatigue and Fracture and Engineering Materials and Structures，1993，16（4）：377-390.

[11]Frendahl M,Rychlik I.Rainflow analysis:Markov method[J].International Journal of Fatigue，1993，15（4）：265-272.

[12]Benasciutti D,Tovo R.Comparison of spectral methods for fatigue analysis of broad-band Gaussian random processes[J].Probabilistic Engineering Mechanics，2006，21（4）：287-299.

[13]Rychlik I.On the narrow-band approximation for expected fatigue damage[J].Probabilistic Engineering Mechanics，1993，8（1）：1-4.

[14]Lutes L D,Sarkani S.Stochastic analysis of structural and mechanical vibrations[M].Oxford：Butterworth-Heinemann,2003：261-272.

[15]姚起杭，姚军.工程结构的振动疲劳问题[J].应用力学学报，2006，23（1）：12-15.YAO Qihang,YAO Jun.Vibration fatigue in engineering structures[J].Chinese Journal of Applied Mechanics，2006，23（1）：12-15.(in Chinese)