航空发动机直通型篦齿径向变形稳健性优化

陈志英，李建福，周 平，刘 勇

（北京航空航天大学能源与动力工程学院，北京100191）

0 引言

篦齿封严结构凭借着结构简单以及在高温和高转速下具有高可靠性等优点在航空发动机中得到了广泛应用[1]。其封严质量直接影响发动机的效率及可靠性，众多学者对影响其封严质量的影响因素进行了大量的研究。纪国剑[2]针对几种典型篦齿封严结构，研究了结构尺寸、压比及转速等参数对篦齿封严特性的影响规律。胡旭东等[3]对篦齿进行了泄漏性实验研究并得出篦齿的封严间隙是影响其密封效果的因素之一。张勃等[4]研究了篦齿几何参数对对流换热系数的影响，得出篦齿封严间隙是影响其变化的主要因素。杜发青等[5]通过研究篦齿几何参数对泄漏特性的影响，发现封严间隙对泄漏特性影响显著。而对于航空发动机涡轮篦齿结构而言，转子运转时在外载荷的作用下产生的径向变形会导致封严间隙变化，进而影响封严效果[6-7]。以上文献研究表明封严间隙变化对封严特性有重要的影响，而篦齿径向变形又是导致封严间隙变化的主要原因，因此对篦齿在动态下的径向变形进行准确估计有助于更加合理地控制封严间隙。由于在工程实践中篦齿结构尺寸、材料以及载荷等参数具有不确定性，因此使得动态下的篦齿径向变形会呈现不确定性，从而影响封严间隙的估计。因此在进行篦齿径向变形计算时必须考虑参数不确定性的影响才更加符合工程实际。

稳健性设计可以有效降低参数变化对目标响应的影响程度[8-9]，其在航空航天领域得到了广泛应用[10-12]，优化结果表明优化后的目标响应对参数变化的敏感性降低。因此对篦齿结构径向变形进行稳健性设计将有效降低参数变化对篦齿径向变形的影响程度，从而准确评估运转状态下的封严间隙变化。对于复杂结构的稳健性优化而言，直接利用有限元方法进行优化求解将非常耗时，不能很好地满足工程应用的需要。而近似模型方法如Kriging、支持向量机以及多项式响应面的出现，很好地解决了复杂结构的优化效率问题，并在工程计算中得到了广泛应用[13-15]。对于高度非线性复杂函数关系的拟合，支持向量机与其他近似模型相比具有小样本、预测精度高等特点[16]，更加适合复杂模型的工程应用计算。

本文提出一种基于最小二乘支持向量机模型的稳健性优化方法，对篦齿结构径向变形进行稳健性优化设计。首先利用LS-SVM模型建立参数与篦齿径向变形之间的近似函数模型，并进行参数灵敏度分析。考虑到输入参数中尺寸变量为区间变量，而其他参数为随机型变量的情况，选择分位数区间法[17]建立稳健性优化模型，然后对建立好的稳健性优化模型进行优化求解。

1 稳健性优化模型

1.1 最小二乘支持向量机

最小二乘支持向量机（LS-SVM）是一种针对非线性函数拟合的高精确度近似模型方法[18]，假定一个样本训练集{xi,yi}（i=1,2,…,N），其中xi∈Rn为样本输入，yi∈Rn为样本输出。根据统计学理论通过把支持向量机的不等式约束变为等式约束，并用平方损失函数代替不敏感损失函数，可得到最小二乘支持向量回归机的数学模型[19]

式中：e=[e1,…,eN]，为预测值与真实值之间的误差；c∈R+，为用来控制模型复杂度和训练误差的正则化参数；φ（xi）为把输入空间中的非线性拟合问题转化为线性拟合问题的变换函数。

求解式（1）之前需要构造一个Lagrange函数

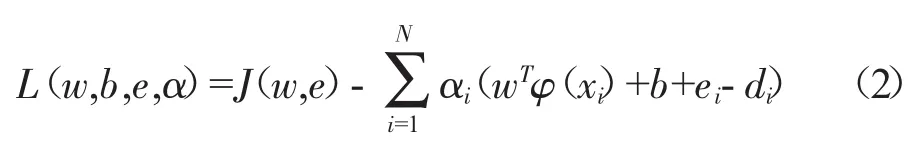
式中：a=[a1,…,aN]T，为 Lagrange 乘子。

式（2）的最优化条件即 Kuhn-Tucker（KT）条件[20]为求解得

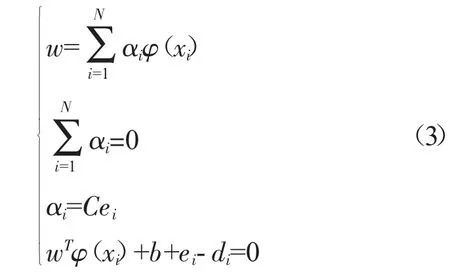
对式（3）中的线性方程组进行求解可得LS-SVM近似模型

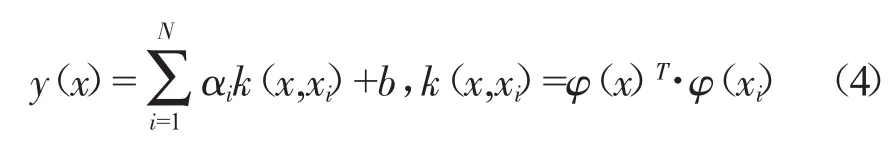
式中：k（x,xi）=φ（x）T·φ（xi），为核函数。

1.2 稳健性优化模型的建立

稳健性优化通过选择合适水平的设计参数使得所有参数变化对目标响应影响程度降低，提出的基于LS-SVM与概率分位数区间方法的稳健性优化技术流程如图1所示。

图1 基于LS-SVM与概率分位数区间法的稳健性优化过程

图1描述了稳健性优化模型建立的过程，其核心点包括：用有限元方法对篦齿结构进行径向变形确定性分析，在考虑各参数不确定性分布的情况下利用拉丁抽样法抽取若干样本，利用抽取的样本建立参数与目标响应之间的LS-SVM近似模型。近似模型与有限元方法相比，在保证一定的计算精度的情况下，可以大大减少优化迭代时间，提高计算效率。

考虑到近似模型预测误差以及各参数具有不同的分布特性，选用分位数区间模型[17]建立稳健性优化模型。分位数区间模型的使用可降低由于参数分布不同以及近似模型计算误差对目标响应统计结果的影响，提高计算结果的可信度。

2 篦齿径向变形的稳健性优化

选取某发动机涡轮转子篦齿封严结构，篦齿环与转子左侧套筒之间为面-面接触式连接，具体结构如图2（a）所示。图2（a）左侧为篦齿封严结构局部示意图，从图中可以看出篦齿封严间隙c随着篦齿径向变形而发生变化。

2.1 有限元模型与参数

首先利用UG软件对选取的某发动机涡轮转子与篦齿结构进行建模，然后导入有限元软件ANSYS中进行热-机械耦合径向变形分析，建立的有限元计算模型如图2（b）所示。其中涡轮盘材料牌号为GH4033，涡轮叶片材料牌号为K419，篦齿材料牌号为GH742。接触问题采用面-面接触并用罚函数法求解，接触摩擦系数取0.3。有限元分析过程中温度载荷通过给定盘心以及叶尖温度以函数插值方式加入到涡轮转子。

图2 直通型篦齿结构

由于篦齿环与涡轮盘套筒的面-面连接特点，涡轮盘套筒的径向变形与篦齿环的径向变形相互影响。在不影响涡轮转子径向尺寸链初始设计的情况下，选取涡轮盘部件5个位置的尺寸作为设计参数，具体选取位置如图2（a）所示。其中X1为轮盘辐板中间位置的轴向尺寸，X2和X3分别为轮盘左侧和右侧套筒边缘到轮盘中心线的轴向尺寸。综合考虑涡轮部件许用强度以及部件质量，以设计参数的初始设计值为优化区间上限进行质量约束，以轮盘强度为约束设定设计参数优化区间下限，具体数值见表1，表中的上限和下限表示设计参数设计点的优化区间，所有尺寸设计点的不确定性区间均为[-0.001 mm,+0.001 mm]。

表1 设计参数的优化区间

考虑到运转状态下转子转速以及温度不确定性对篦齿径向变形的影响，将转子转速ω、盘心温度t1、叶尖温度t2也作为随机变量，具体数值见表2[21]。而涡轮盘、涡轮叶片以及篦齿的材料参数也具有不确定性,因此选择弹性模量E、密度ρ、热传导率λ、线性膨胀系数α作为材料的随机参数，具体数值见表3[22]。

表2 随机参数温度以及转速均值及标准差

表3 涡轮叶片、涡轮盘、篦齿材料的随机参数均值及标准差

2.2 LS-SVM模型的建立

首先利用有限元方法对篦齿径向变形进行计算抽取150组训练样本，然后采用LS-SVM模型建立参数与变形之间的近似函数。利用有限元方法随机抽取10组样本对建立的LS-SVM近似模型进行预测精度验证，验证结果如图3所示。通过计算得到预测值与验证样本均方根的误差为4.5×10-3，其最大相对误差小于1%。

2.3 参数灵敏度分析

考虑到LS-SVM近似模型难以求导，文中选用Morris方法求解参数对变形的灵敏度[23]，并假设各参数之间相互独立。求解的参数灵敏度如图4所示。

图4中1～3依次为设计参数Xi（i=1,2,3），可以看出设计参数中X1灵敏度最大；其次为X2和X3。4～6分别为转速ω、盘心温度t1、叶尖温度t2的灵敏度；7～18依次为涡轮叶片、涡轮盘、篦齿的密度ρ，以及线性膨胀系数α、弹性模量Ε、热导率λ的灵敏度。

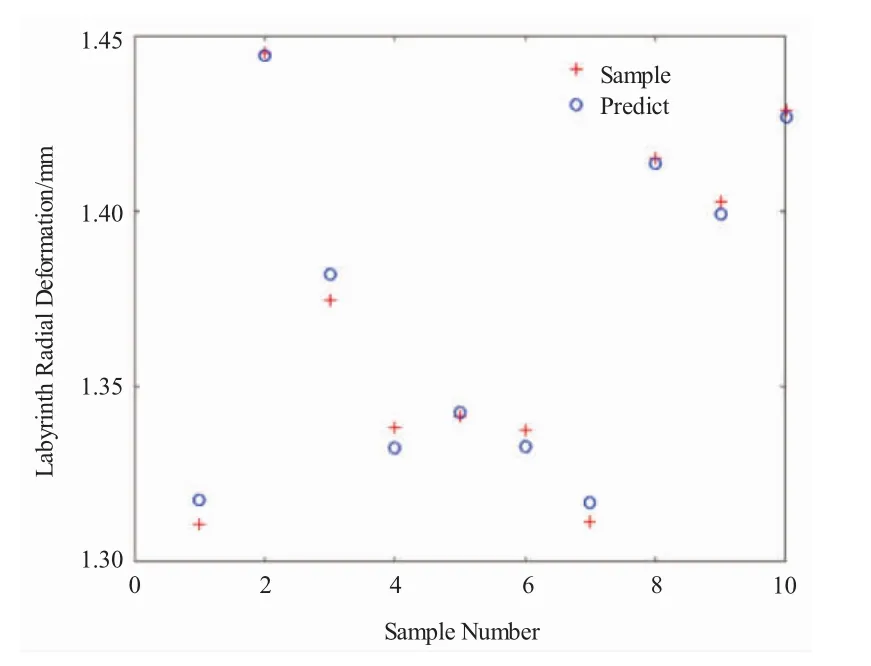
图3 LS-SVM预测值与验证样本

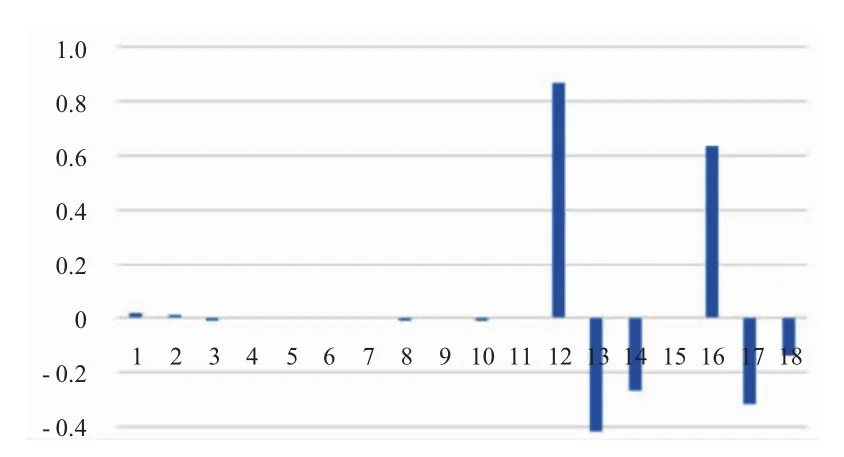
图4 参数灵敏度分析结果

从图4中可见，涡轮盘线膨胀系数的影响最大，篦齿环的线性膨胀系数的影响次之，这是由于在运转情况下，涡轮盘与篦齿环装配处的涡轮盘左侧套筒的径向变形量小于篦齿环的径向变形量，因此轮盘左侧套筒的径向变形对篦齿径向变形起主导作用；其次，涡轮盘和篦齿弹性模量以及热传导率的影响也较为明显，而其余参数对变形影响相对于以上参数都较小。

2.4 篦齿径向变形的稳健性优化模型

对于工程实际而言，虽然数据呈现某种分部特性，但其不确定性区间也是有界的，并不是随着分布特性一直延伸。因此选用工程常用的[μ-3σ,μ+3σ]区间来描述其不确定性波动范围，对于正太分布而言，将其转换为分位数区间，其模型为[W0.0013,W0.9987]。因此，对建立好的LS-SVM近似模型进行蒙特卡洛法进行104次抽样分别计算W0.0013和W0.9987分位数进而计算分位数区间值，建立好的优化模型为

式中：X为设计参数向量，其优化区间见表1；z为随机参数向量，见表为分位数区间；函数 g（X，z）与g*分别为转子应力与许用应力值。

2.5 结果与分析

建立好稳健性优化模型后，采用果蝇优化算法[24]对优化模型进行优化迭代求解，优化前后蒙特卡洛抽样后的篦齿径向变形直方图如图5所示，其中图5（a）为优化前，图5（b）为优化后。优化前后参数与概率分位数区间数值见表4。从图5中可见，优化前后的直方图中间部分基本服从正态分布，而边缘数据呈现出一定的离散随机性，如果直接采用概率标准差作为优化目标结果将随着边缘数据离散随机程度呈现一定的随机性。而概率分位数区间的方法可以剔除边缘数据影响，因此统计结果将更为稳定和精确。

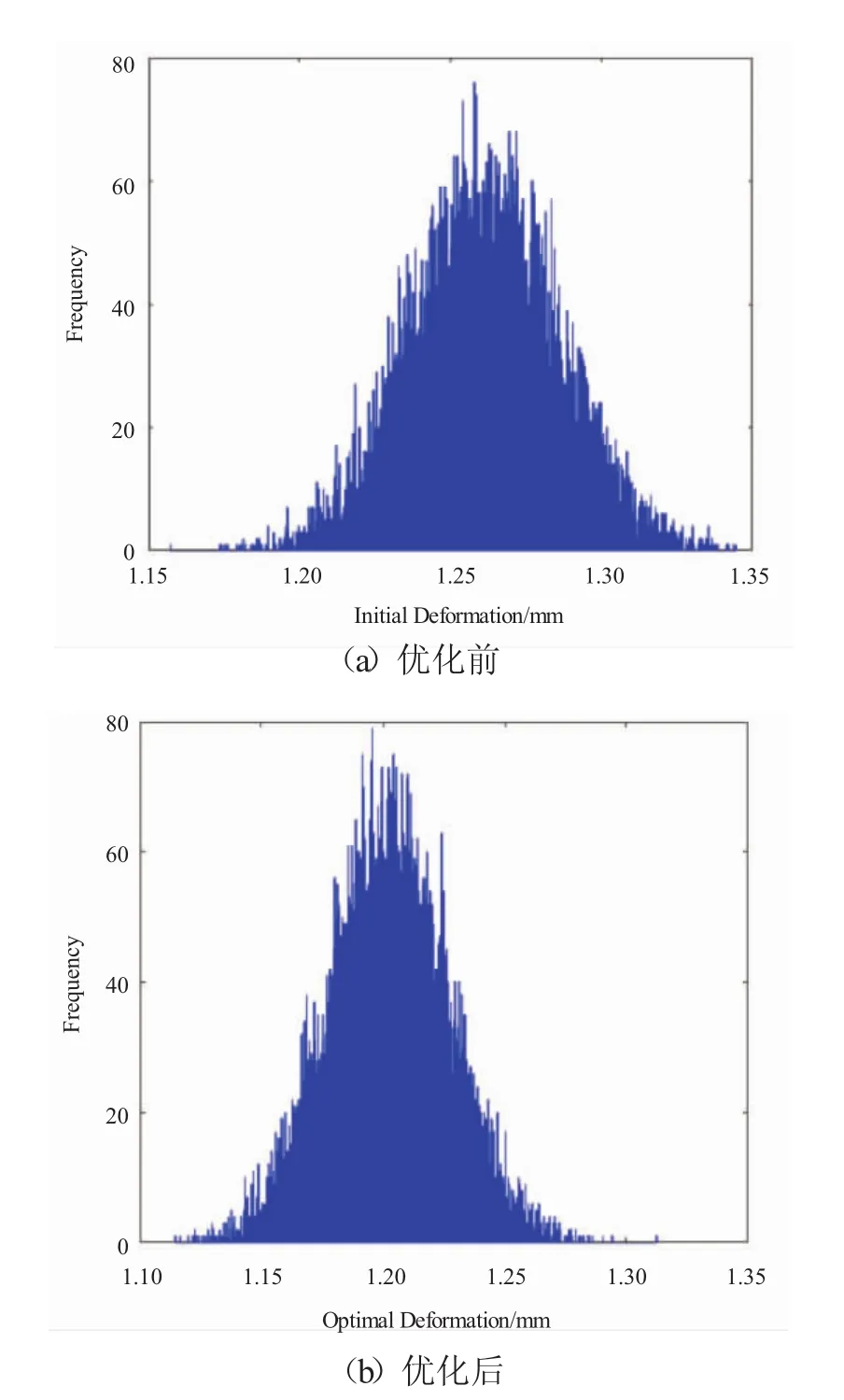
图5 蓖齿径向变形

表4 稳健性优化前后的结果

从表4中可见，优化后的径向变形分位数区间比优化前减少了6%，有效降低了篦齿径向变形对参数变化的敏感性，可以更为精确地估计发动机运转状态下封严间隙变化的情况，并为合理控制封严间隙提供一定的参考。

为了更直观地反映稳健性优化后参数对篦齿径向变形的影响程度，根据图4选取篦齿径向变形相对较大的参数，对其优化后的参数灵敏度进行求解并与优化前进行对比，具体数值见表5。

表5 优化前后参数灵敏度的分析结果

表5中材料参数下标d和l分别表示涡轮盘和篦齿，从优化前后灵敏度数据来看，对篦齿变形影响较大的参数的灵敏度值都有不同程度的减小。优化前后灵敏度分析的结果也验证了基于概率分位数区间的稳健性优化方法的有效性。

3 结论

（1）本文针对篦齿结构，在考虑参数不确定性的情况下，对篦齿转子结构径向变形进行了稳健性优化，优化后的分位数区间比优化前减少了6%，有效降低了参数变化对篦齿径向变形的影响程度，为合理设计以及控制篦齿封严间隙提供了一定参考。

（2）提出的基于LS-SVM模型的稳健性优化方法可有效地解决篦齿等复杂结构在进行优化分析时迭代时间较长的问题，在保证计算精度的情况下可提高计算效率。

（3）在后续计算中还需对篦齿封严静子结构径向变形进行分析，以便对篦齿封严间隙进行精确估计。

[1]王洪玉,秦朝烨,褚福磊,等.航空发动机直通型篦齿封严鼓筒气动力分析[J].工程力学,2013，30(12):267-274.WANG Hongyu,QIN Zhaoye,CHU Fulei,et al.Aerodynamic analysis of straight-through labyrinth seal of the drum of an aeroengine[J].Engineering Mechanics,2013,30(12):267-274.（in Chinese）

[2]纪国剑.航空发动机典型篦齿封严泄漏特性的数值和实验研究[D].南京：南京航空航天大学,2008.JI Guojian.Numerical and dxperimental investigation of sealing characteristics on typical labyrinth seals in aeroengine[D].Nanjing:Nanjing University of Aeronautics and Astronautics，2008.（in Chinese）

[3]胡东旭,贾力,杨立新.篦齿封严泄漏特性的实验 [J].航空动力学报,2014,29（3）:549-555.HU Dongxu,JIA Li,YANG Lixing.Experiment on leakage characteristics in labyrinth seal[J].Journal of Aerospace Power,2014,29（3）:549-555.（in Chinese）

[4]张勃,吉洪湖,杜发青,等.基于正交法的直通篦齿封严齿形几何参数对换热特性影响的试验研究 [J].机械工程学报,2013,49（4）:134-139.ZHANG Bo，JI Honghu，DU Faqing，et al.Orthogonal design experimental investigation of effect of tip geometrical parameters on heat transfer of straight-through labyrinth[J].Journal of Mechanical Engineering,2013,49（4）:134-139.（in Chinese）

[5]杜发青,吉洪湖,帅海山,等.齿形几何参数对直通篦齿封严泄漏特性影响的正交实验[J].航空动力学报,2013,28（4）:825-831.DU Faqing,JI Honghu,SHUAI Haishan,et al.Orthogonal experiment of effect of fin geometrical parameters on leakage of straight-through labyrinth seals[J]Journal of Aerospace Power,2013,28（4）:825-831.（in Chinese）

[6]王鹏飞,刘玉芳,郭文,等.高转速对直通型篦齿封严特性影响的试验研究[J].燃气涡轮试验与研究,2007，20（2）:45-48.WANG Pengfei,LIU Yufang，GUO Wen，et al.Influence of high rotational speeds on the labyrinth sealing characteristics[J].Gas Turbine Experiment&Research,2007，20（2）:45-48.（in Chinese）

[7]Waschka W,Wittig S,Kim S.Influence of high rotational speeds on the heat transfer and discharge coefficients in labyrinth seals[R].ASME 1990-GT-330.

[8]Beyer H G,Sendhoff B.Robust optimization A comprehensive survey[J].Computer Methods in Applied Mechanics and Engineering,2007,196（33）:3190-3218.

[9]Robinson T J,Borror C M,Myers R H.Robust parameter design:a review[J].Quality and Reliability Engineering International,2004,20（1）:81-101.

[10]刘艳,白俊强,华俊,等.基于Stochastic Kriging的柔性机翼稳健性优化设计[J].西北工业大学学报,2015，33（6）:906-912.LIU Yan,BAI Junqiang，HUA Jun，et al.Robust optimization of flexible wing using stochastic kriging surrogate model[J].Journal of Northwestern Polytechnical University,2015,33（6）:906-912.（in Chinese）

[11]贺谦,李元生,温志勋,等.涡轮叶片多学科可靠性及稳健设计优化[J].推进技术,2010，31（2）:193-197.HE Qian,LI Yuansheng,WEN Zhixun,et al.Multidisciplinary probabilistic and robust design optimization for turbine blade[J].Journal of Propulsion Technology，2010,31（2）:193-197.（in Chinese）

[12]贺波勇,李海阳,张波.载人登月转移轨道偏差传播机理分析与稳健性设计[J].物理学报,2013,62（19）:83-90 HE Boyong,LI Haiyang,ZHANG Bo.Analysis of transfer orbit deviation propagation mechanism and robust design for manned lunar landing[J].Acta Physica Sinica，2013,62（19）:83-90.（in Chinese）

[13]苗恩铭,龚亚运,徐祗尚,等.数控机床热误差补偿模型稳健性比较分析[J].机械工程学报,2015，51（7）:130-135.MIAO Enming，GONG Yayun，XU Zhishang，et al.Comparative analysis of thermal error compensation model robustness of CNC machine tools[J].Journal of Mechanical Engineering,2015,51（7）：130-135.（in Chinese）

[14]李小刚,程锦,刘振宇,等.基于双层更新Kriging模型的机械结构动态特性稳健优化设计[J].机械工程学报,2014,50（3）:165-173.LI Xiaogang，CHENG Jin，LIU Zhenyu,et al.Robust optimization for dynamic characteristics of mechanical structures based on double renewal kriging model[J].Journal of Mechanical Engineering,2014,50（3）:165-173.（in Chinese）

[15]彭茂林,杨自春,曹跃云,等.基于响应面法的可靠性稳健设计优化[J].航空动力学报,2013,28（8）:1784-1790.PENG Maolin,YANG Zichun，CAO Yueyun,et al.Reliability robust design optimization based on response surface method[J].Journal of Aerospace Power,2013,28（8）:1784-1790.（in Chinese）

[16]Jin R,Chen W,Simpson T W.Comparative studies of metamodeling techniques under multiple modeling criteria[J].Structural&Multidisciplinary Optimization,2000,23（1）:1-13.

[17]刘春涛,林志航,周春景.具有随机型和区间型干扰因素的产品健壮设计研究[J].中国机械工程,2007,18（5）:505-509.LIU Chuntao,LIN Zhihang，ZHOU Chunjing.Study on product robust design with a mixture of random and interval noise factors[J].China Mechanical Engineering,2007,18（5）:505-509.（in Chinese）

[18]Suykens J A K,Gestel T V,Brabanter J D,et al.Least squares support vector machines[J].Euphytica,2002,2（2）:1599-1604.

[19]赵永平.支持向量回归机及其在智能航空发动机参数估计中的应用[D].南京：南京航空航天大学,2009.ZHAO Yongping.Support vector regressions and their applications to parameter estimation for intelligent aeroengines[D].Nanjing:Nanjing University of Aeronautics and Astronautics，2009.（in Chinese）

[20]Suykens J A K,Brabanter J D,Lukas L,et al.Weighted least squares support vector machines:robustness and sparse approximation[J].Neurocomputing,2002,48（1-4）:85-105.

[21]费成巍,白广忱.航空发动机涡轮叶片径向变形的概率分析[J].航空发动机,2012,38（1）:17-20.FEI Chengwei，BAI Guangchen.Probability analysis of radial deformation of aeroengine turbine blades[J].Aeroengine,2012,38（1）:17-20.（in Chinese）

[22]Fei C W,Bai G C.Distributed collaborative probabilistic design for turbine blade-tip radial running clearance using support vector machine of regression[J].Mechanical Systems and Signal Processing,2014,49（1）:196-208.

[23]Zhan C S,Song X M,Xia J,et al.An efficient integrated approach for global sensitivity analysis of hydrological model parameters[J].Environmental Modelling&Software,2013,41:39-52.

[24]Pan W T.A new fruit fly optimization algorithm:taking the financial distress model as an example [J].Knowledge-Based Systems,2012,26（2）:69-74.