晶格失配应力对单晶(BiTm)3(GaFe)5O 12膜磁畴结构的影响∗
2018-06-19郝俊祥杨青慧张怀武文岐业白飞明钟智勇贾利军马博吴玉娟
郝俊祥 杨青慧 张怀武 文岐业 白飞明 钟智勇 贾利军马博 吴玉娟
1 引 言
钇铁石榴石膜具有优越的磁性能和广泛的应用范围,是研究最充分的磁性薄膜材料之一.薄膜的易磁化轴一般在面内,但石榴石薄膜可利用单轴各向异性较强的Bi3+或其他稀土离子取代十二面体位的Y3+离子,从而实现易磁化轴垂直于膜面,这一特性不仅在磁泡存储器[1−3]和磁光器件等[4,5]方面得到应用,而且在自旋电子学领域也具有很大的发展前景[6].但薄膜单轴磁各向异性的控制一直是应用过程中的关键挑战之一.液相外延(LPE)工艺可以使外延膜感生出单轴各向异性,有利于石榴石膜的垂直各向异性产生,成为了实现石榴石膜垂直磁化的一种关键制造技术[7].然而LPE工艺对外延膜与衬底之间的晶格匹配要求较高,尤其是在厚膜制备工艺中,晶格失配情况是外延厚膜能否成功的关键因素[8].
LPE石榴石膜一般选择钆镓石榴石(GGG)衬底,因为GGG衬底同属石榴石,其力学和化学性质与石榴石匹配,且其晶格常数与钇铁石榴石差别不大,但在GGG衬底上LPE石榴石膜仍属于异质外延.异质外延中难以避免的晶格失配会在薄膜与衬底之间产生晶格失配应力,从而影响成膜的质量和性质[9−12],如引起易磁化轴的偏转等.对于LPE工艺,在晶格失配情况下,外延膜的垂直各向异性不仅受到立方磁晶各向异性、生长各向异性和形状各向异性的影响,而且还受到晶格失配应力的影响.同时,失配应力对垂直各向异性的作用也会对磁畴结构产生影响.如何通过控制失配应力来控制薄膜的单轴各向异性是本文研究的重点.本文利用LPE工艺在GGG衬底上以不同生长速率制备了(BiTm)3(GaFe)5O12膜,生长速率的不同导致了进入薄膜晶格的离子数量有所变化,从而引起薄膜与衬底间晶格失配应力的变化,系统分析研究了晶格失配应力对其磁畴结构的影响,发现失配应力对单轴各向异性的影响是改变磁畴结构的根本原因.
2 实 验
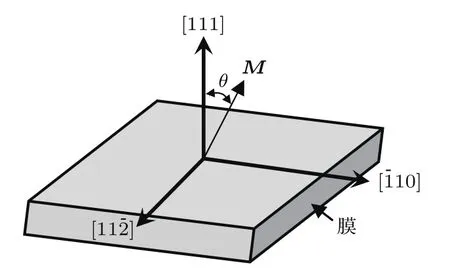
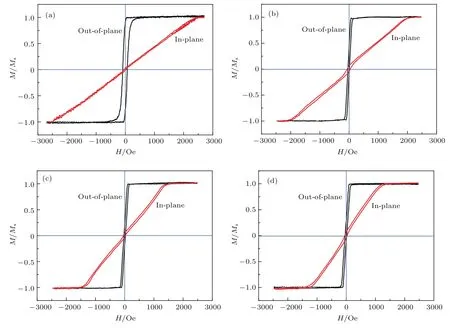
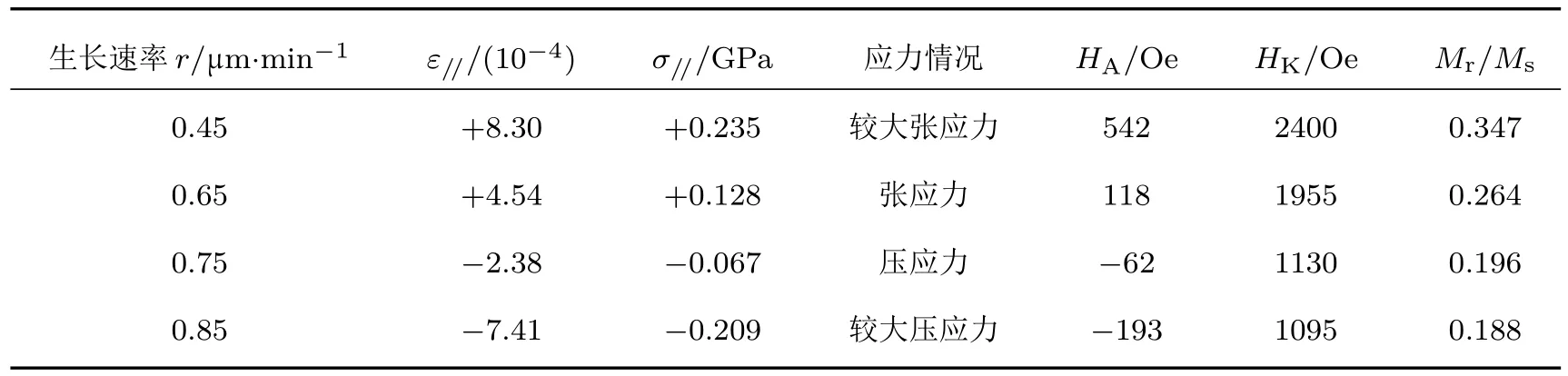
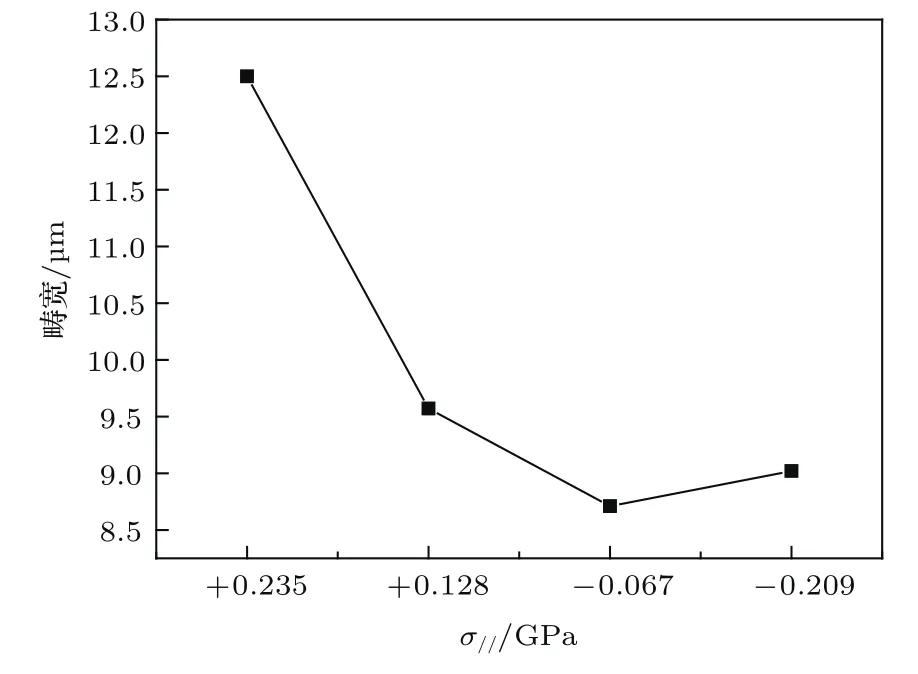
利用LPE工艺在GGG(111)衬底上外延了单晶(BiTm)3(GaFe)5O12膜.实验中以高纯(>99.999%)Ga2O3,Tm2O3,Fe2O3,Bi2O3为原料,根据配方:(BixTm3−x)(GayFe5−y)O12(0 表1 样品膜的生长条件及相关信息Table 1.Growth conditions and related information of sample fi lms. 薄膜的晶格失配情况应用高分辨率X射线衍射仪(HRXRD,D1 Evolution,JVS,Germany)测量其摇摆曲线表征;磁滞回线应用振动样品磁强计(VSM,BHV525,IWATSH,Japan)测量;磁畴结构由磁光克尔测量系统(MOKE,NanoMOKE3,Durham,UK)观察退磁态样品膜的极向克尔旋转效应得到,测试过程中无外加磁场和直流偏场,测试波长为660 nm. 对于LPE生长的膜,生长速率不同直接导致了进入晶格的各离子含量的微小变化,从而引起薄膜晶格的变化,进而决定了薄膜与衬底之间的晶格失配变化,而晶格失配的变化又导致了膜内应力的变化.图1是测得的以不同生长速率生长的单晶(BiTm)3(GaFe)5O12膜的HRXRD摇摆曲线,测试时以衬底GGG(444)衍射峰角2θs=51.073◦为中心进行摇摆测试.由图1可知,随着生长速率增大,单晶(BixTm3−x)(GayFe5−y)O12膜的衍射峰移向较低角度,说明膜的晶格变大.因为随着生长速率增大(熔体过冷度增大),薄膜含量中的x变大,y微量减小[14−16],结合膜内离子半径排序:Bi3+(108Å)>Tm3+(86.9Å)>Fe3+(64Å)>Ga3+(62Å),可知膜内Bi3+含量增加导致的晶格膨胀是晶格常数变大的主要原因. 晶格失配∆a⊥=as−af⊥,其中af⊥为应变状态下外延膜的晶格常数,as为衬底晶格常数.所用GGG(111)衬底as=12.383Å,厚度为500µm(远大于膜厚10µm,假设应变过程中衬底晶格常数不变).已有研究表明[17−19],当∆a⊥>0时,膜受到张应力,如图2(a)所示;当∆a⊥<0时,膜受到压应力,如图2(b)所示.其中,af0为自由状态下膜的晶格常数,ε⊥为垂直膜面方向(面外)的应变,ε//为平行膜面方向(面内)的应变,σ//为面内应力. 图1 不同生长速率(BiTm)3(GaFe)5 O12膜的摇摆曲线Fig.1.X-ray rocking curves of(BiTm)3(GaFe)5O12 fi lms with diff erent growth rates. 晶格失配∆a⊥与失配应力σ//的计算公式[20−24]为 其中θf为膜的半衍射峰位角;∆θ为衍射峰位角度差,可直接从摇摆曲线中读出;ν=0.286为泊松比;弹性模量[25]C11=2.68×1011N/m2,C12=1.106×1011N/m2,C44=0.766×1011N/m2. 不同生长速率样品膜的∆a⊥和σ//通过(1a)—(1f)式计算,其结果列于表2中. 由表2可知,晶格失配∆a⊥=(−17.4—(+19.5))×10−3Å处于Besser’s I区域内,热膨胀系数失配对应力的作用可忽略,膜内应力仅由晶格失配引起,∆a⊥与σ//呈线性相关[26].此外,在生长速率r=0.45µm/min时,∆a⊥=+19.5×10−3Å,超出了LPE完整膜的晶格失配理论极限[27]∆a⊥(per)=[−18.0—(+15.0)]×10−3Å,对应膜表面出现了少量裂纹. 图2 晶格失配(∆a⊥)下膜内应力(σ//)示意图 (a)∆a⊥ >0,σ//为张应力;(b)∆a⊥ <0,σ//为压应力Fig.2.Schematic diagram of stress(σ//)of fi lms with lattice mismatch(∆a⊥):(a)∆a⊥ >0,σ//is tensile stress;(b)∆a⊥ <0,σ//is compressive stress. 表2 晶格失配(∆a⊥)和应力(σ//)的计算结果Table 2.Calculation of lattice mismatch(∆a⊥)and stress(σ//). 在磁性材料中,膜内总体自发磁化矢量M直接决定着易磁化轴的取向,将M 与膜面法向间夹角定义为θ,如图3所示.总的磁晶各向异性可由磁晶各向异性等效场HK表示,(111)晶面上的单晶(BixTm3−x)(GayFe5−y)O12膜面外HK越大,表明θ越小.LPE单晶石榴石膜的磁晶各向异性主要受到立方磁晶各向异性、感生单轴各向异性、形状磁各向异性和应力磁各向异性的影响[28].因本文样品膜厚度较大(约10µm),形状各向异性被忽略.H K可表示为[29−33] 其中Kgu为生长诱导的单轴各向异性常数;Kλu为应力诱导的单轴各向异性常数;K1(x,y)为一阶立方磁晶各向异性常数;A,B,C分别为Kgu,Kλu,K1(x,y)的转换系数;HA为应力诱导的有效各向异性场;λ111(x,y)为[111]晶向的磁致伸缩系数;M为自发磁化强度.此外,K1(0,0)<0,使得立方晶体的易磁化轴为面外[6];Kgu>0,生长诱导的单轴各向异性垂直于膜面[34];λ111(0,0)<0,张应力σ//>0(压应力σ//<0)诱导的单轴各向异性垂直于(平行于)膜面[35−38]. 图3 膜内总自发磁化矢量M取向示意图Fig.3.Schematic diagram of total spontaneous magnetization M orientation in the fi lm. 图4 为不同生长速率r和失配应力σ//样品膜的面内和面外M-H曲线,其中HK通过磁化曲线交点法得到,Mr/Ms为面外M-H曲线的剩磁比,HK和Mr/Ms均列于表3中.由图4(a)—(d)可知,所有样品膜的易磁化轴为面外,总的磁晶各向异性为垂直各向异性.Mr/Ms和HK随着σ//数值的减小而降低,说明随着膜生长速率增大,垂直各向异性逐渐降低,M与膜面法向间夹角θ逐渐增大. 由(2a)—(2d)式可知,随着生长速率增大(x增大,y减少),CK1(x,y)和AKgu增大[39],有利于使θ减小,HK增大,薄膜的易磁化轴应转向面外,同时更利于形成磁泡畴;但这与我们的实验数据(见图4)相悖.因此得出结论:以LPE方法生长的单晶石榴石膜,其生长速率增加导致的应力各向异性场HA在其中发挥了更大的作用,很大程度上决定了HK的改变.HA属于HK的一部分,虽然|λ111(x,y)|增大,但HA同时又受到σ//的影响,因此,当σ//>0(σ//<0) 时,HA>0(HA<0),有利于使θ减小(增大),对应HK增大(减小).利用Kubota等[17,40]建立的计算模型,通过(2b)式算得HA值,列于表3中.结合表3可知,HK与HA的变化趋势一致,σ//对HK的变化起到了决定性作用,即σ//直接决定了θ的变化趋势. 图4 不同生长速率r和失配应力σ//膜的面外(黑线)和面内(红线)方向的M-H曲线 (a)r=0.45µm/min,σ//=+0.235 GPa;(b)r=0.65 µm/min,σ//=+0.128 GPa;(c)r=0.75 µm/min,σ//= −0.067 GPa;(d)r=0.85µm/min,σ//= −0.209 GPaFig.4.Hysteresis curves of fi lms with diff erent growth rates r and diff erent mismatch stressσ//along out-ofplane(black)and in-plane(red)directions:(a)r=0.45 µm/min,σ//=+0.235 GPa;(b)r=0.65 µm/min,σ//=+0.128 GPa;(c)r=0.75µm/min,σ//=−0.067 GPa;(d)r=0.85µm/min,σ//= −0.209 GPa. 表3 应力诱导的有效各向异性场(H A)、磁晶各向异性等效场(H K)和剩磁比(M r/M s)Table 3.Stress-induced eff ective anisotropy fi eld(H A),total magnetocrystalline anisotropy equivalent fi eld(H K)and remanence ratio(M r/M s). 图4(a)中,膜在较大张应力(σ//=+0.235 GPa)下,Mr/Ms和HK均为最大值,表明膜垂直各向异性最大,θ最小;图4(d)中,膜在较大张应力(σ//=−0.209 GPa)下,Mr/Ms和HK均为最小值,表明膜垂直各向异性最小,θ最大.虽然较大压应力引起了Kλu变化,使得θ变大,一定范围内调整了垂直各向异性的方向,但因变化量很小,始终无法克服Kgu诱导的垂直各向异性,于是,面外始终为易磁化轴[34]. 图5是相同膜厚、不同生长速率r和失配应力σ//样品膜的磁畴结构图.由图5可知,随着σ//值减小,晶格失配应力由较大张应力变为较大压应力,磁畴的形状发生显著变化,由磁泡畴(图5(a))先转变成螺旋状迷宫畴(图5(b)),然后转变为过渡态的部分弯曲条状畴(图5(c)),最终转变为整齐排列的条状畴(图5(d)).图5(a)中大量磁泡畴的出现,说明在较大的张应力(σ//=+0.235 GPa)作用下,膜内满足了垂直各向异性极大值的条件,θ达到了最小值[41],这与前文磁性能变化相对应.此外,图5(a)中的几条条状畴是因膜面裂纹产生.同理,图5(b)—(d)分别反映的是在较小张应力下磁畴为螺旋状迷宫畴,晶格失配最小的压应力下磁畴为过渡态的部分弯曲条状畴,在较大压应力下磁畴为整齐排列的条状畴.图5(a)—(d)中磁畴图案的亮色和暗色区域几乎相同,其对比度模式与垂直磁化膜预期的一致,可知这4种磁畴形状都是以面外为易磁化轴;磁畴形状和宽度分布均匀,说明晶格失配应力在膜内均匀分布.结合前文可知,σ//对Kλu的改变影响了垂直各向异性,最终影响了磁畴的形状,同时,磁畴形状变化也反映了垂直各向异性的变化.磁畴结构对垂直各向异性的变化十分灵敏,说明调整膜内应力是控制磁畴结构的有效手段之一. 图5 不同生长速率r和失配应力σ//膜的磁畴结构 (a)r=0.45 µm/min,σ//=+0.235 GPa;(b)r=0.65 µm/min,σ//=+0.128 GPa;(c)r=0.75 µm/min,σ//= −0.067 GPa;(d)r=0.85µm/min,σ//= −0.209 GPaFig.5.Magnetic domain of fi lms with diff erent growth rates r and diff erent mismatch stressσ//: (a)r =0.45 µm/min,σ//=+0.235 GPa;(b)r=0.65 µm/min,σ//= +0.128 GPa;(c)r= 0.75 µm/min, σ//=−0.067 GPa;(d)r=0.85µm/min,σ//= −0.209 GPa. 图6是样品膜磁畴宽度与失配应力σ//的关系曲线,可知随着σ//值的减小(晶格失配应力由较大张应力变化为较大压应力),畴宽先减小后增大.较大张应力时(σ//=+0.235 GPa),磁泡尺寸最大约为12.5µm,超过了膜厚尺寸.膜内应力最小时(σ//=−0.067 GPa),畴宽达到最小值.可见膜内应力越大,畴宽越大,这可能是因为晶格失配应力改变了总体单轴各向异性引起的[40]. 图6 样品膜的磁畴宽度与失配应力σ//的关系Fig.6.Relationship between magnetic domain width and mismatch stressσ//in the fi lms. 研究了晶格失配应力对外延单晶(BiTm)3(GaFe)5O12膜磁各向异性及磁畴结构的影响.实验发现,Bi3+含量随着生长速率增加而增大,使得晶格常数增大,从而改变膜与衬底之间的晶格失配应力;晶格失配应力较之立方磁晶各向异性和生长各向异性会在更大程度上影响膜的单轴各向异性,是改变畴结构的根本原因;晶格失配张应力是增强垂直各向异性的有效手段,当生长诱导的垂直各向异性不足时,磁泡畴只有在较大张应力下才能产生;此外,虽然晶格失配压应力可以降低垂直各向异性,但始终无法克服生长诱导的单轴各向异性,最终形成整齐排列的条状畴;因磁畴内磁矩也受到失配应力影响,失配应力越大磁畴越宽.总之,晶格失配在异质外延中非常普遍,掌握失配应力对薄膜单轴各向异性和磁畴结构的控制手段,对改变材料结构和性能有重大意义. [1]Bobeck A H 1967 Bell Syst.Tech.J.46 1901 [2]Konishi S 1983 IEEE Trans.Magn.M AG-19 1938 [3]Davies J E,Giess E A 1975 J.Mater.Sci.10 2156 [4]Paroli P 1984 Thin Solid Films 114 187 [5]Aichele T,Lorenz A,Hergt R,Goernert P 2003 Cryst.Res.Technol.38 575 [6]Avci C O,Quindeau A,Pai C F,Mann M,Caretta L,Tang A S,Onbasli M C,Ross C A,Beach G 2016 Nat.Mater.16 309 [7]Rosencwaig A,Tabor W J 1971 J.Appl.Phys.42 1643 [8]Matthews J W,Klokholm E 1972 Mater.Res.Bull.7 213 [9]Liu X,Sasaki Y,Furdyna J K 2003 Phys.Rev.B 67 205204 [10]Stone P R,Dreher L,Beeman J W,Yu K M,Brandt M S,Dubon O D 2010 Phys.Rev.B 81 205210 [11]Dho J,Hur N H 2007 J.Magn.Magn.Mater.318 23 [12]Jung C U,Yamada H,Kawasaki M,Tokura Y 2004 Appl.Phys.Lett.84 2590 [13]Blank S L,Nielsen J W 1972 J.Cryst.Growth 17 302[14]Tian L G,Liu X L,Xu S S,Han X X 1989 Acta Phys.Sin.38 1704(in Chinese)[田亮光,刘湘林,许顺生,韩效溪1989物理学报38 1704] [15]Hansen P,Witter K,Tolksdorf W 1983 Phys.Rev.B 27 4375 [16]Hansen P 1974 J.Appl.Phys.45 3638 [17]Kubota M,Shibuya K,Tokunaga Y,Kagawa F,Tsukazaki A,Tokura Y,Kawasaki M 2013 J.Magn.Magn.Mater.339 63 [18]Guduru P R,Chason E,Freund L B 2003 J.Mech.Phys.Solids 51 2127 [19]Wagner G,Gottschalcrt V,Rhan H,Paufl er P 2010 Phys.Stat.Sol.112 519 [20]Yang Q H,Zhang H W,Liu Y L,Weng Q Y,Ji H 2008 The Fourth National Congress and academic conference of China Crystal Society Mount Huangshan,China 2008,p274(in Chinese)[杨青慧,张怀武,刘颖力,文岐业,姬洪2008中国晶体学会全国会员代表大会暨学术会议中国黄山,2008,第274页] [21]Luchechko A P,Syvorotka I I,Zakharko Y,Syvorotka I M 2013 Solid State Phenom.200 215 [22]Navarro-Quezada A,Rodríguez A G,Vidal M A,Navarro-Contreras H 2006 J.Cryst.Growth 291 340 [23]Anastassakis E 1990 J.Appl.Phys.68 4561 [24]Mermoux M,Crisci A,Baillet F,Destefanis V,Rouchon D,Papon A M,Hartmann J M 2010 J.Appl.Phys.107 013512 [25]Bateman T B 1966 J.Appl.Phys.37 2194 [26]Makino H,Hibiya T,Matsumi K 1974 AIP Conf.Proc.18 80 [27]Randles M M 1978 Liquid Phase Epitaxial Growth of Magnetic Garnets(Vol.1)(Heidelberg:Springer-Verlag)pp80–81 [28]Capper P,Mauk M 2007 Liquid Phase Epitaxy of Electronic,Optical and Optoelectronic Materials(England:John Wiley&Sons Ltd)pp333–334 [29]Tkachuk S,Fratello V J,Kraff t C,Lang G,Mayergoyz I D 2009 IEEE Trans.Magn.45 4238 [30]Heinz D M,Besser P J,Owens J M,Mee J E,Pulliam G R 1971 J.Appl.Phys.42 1243 [31]Hansen P,Witter K,Tolksdorf W 1984 J.Appl.Phys.55 1052 [32]Hansen P,Tolksdorf W,Witter K,Robertson J 1984 IEEE Trans.Magn.M A G-20 1099 [33]Wen D,Zhang H,Hui X,Wang Y,Zhong Z,Bai F 2014 IEEE Trans.Magn.50 2801804 [34]Hansen P,Klages C,Witter K 1988 J.Appl.Phys.63 2058 [35]Nistor I,Kraff t C,Rojas R,Mayergoyz I D 2004 IEEE Trans.Magn.40 2832 [36]Wen D,Zhang H,Yang X,LüQ,Bai F 2017 J.Alloys Compd.690 836 [37]Zhu J,Su Y C,Pan J,Feng G L 2013 Acta Phys.Sin.62 167503(in Chinese)[朱洁,苏垣昌,潘靖,封国林2013物理学报62 167503] [38]Shen D F,Du T D,Wang L J,Zhang W Z 1991 Acta Phys.Sin.40 653(in Chinese)[沈德芳,杜腾达,王丽娟,张伟珠1991物理学报40 653] [39]Hansen P,Witter K 1985 J.Appl.Phys.58 454 [40]Kubota M,Tsukazaki A,Kagawa F,Shibuya K,Tokunaga Y,Kawasaki M,Tokura Y 2012 Appl.Phys.Express 5 103002 [41]Mee J E,Pulliam G R,Archer J L,Besser P J 1969 IEEE Trans.Magn.M ag-5 717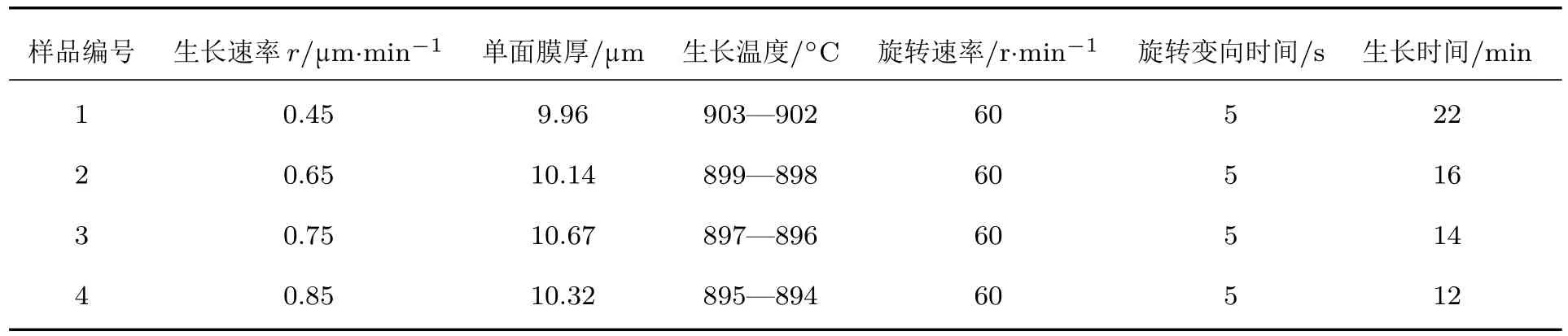
3 结果和讨论
3.1 膜内应力分析




3.2 磁晶各向异性分析

3.3 磁畴结构分析

4 结 论
