油滴撞击油膜层内气泡的变形与破裂过程的数值模拟∗

周剑宏 童宝宏† 王伟 苏家磊

1 引 言

随着工业化水平的提高,人们对于机械产品的安全性、可靠性、节能性以及服役寿命等提出了更高的要求.据统计,在工业生产中约50%的设备损坏是由磨损引起的.润滑作为一种减小摩擦和降低磨损的有效手段,普遍应用于工业生产中.在对旋转工作的机械零部件和设备进行润滑时将不可避免地涉及油滴撞击油膜的现象.例如,在对航空发动机的轴承进行喷油润滑时,为防止润滑油泄漏引起焦化和着火等现象,常采用空气系统对轴承室进行密封,使轴承室内部处于复杂的油-气混合状态,具体表现为油滴和油膜间的相互作用行为[1];在对齿轮、涡轮等减速器装置进行飞溅润滑时,机箱中旋转的零部件将润滑油雾化成油滴带到摩擦副上形成自动润滑,部分油滴将会与机箱中的油膜发生碰撞行为;在对高速电主轴进行油-气润滑时,零部件表面受连续油滴撞击并形成润滑油膜层,随时间变化,后续油滴常与沉积的油膜层发生作用.

目前,在学术期刊上较常见的是非油类液滴与液膜的碰撞行为研究,其研究内容主要分为两个方面:一方面是关注液滴撞击液膜的流动行为;另一方面则集中考察气泡夹带现象.

针对液滴撞击液膜的流动行为已开展了大量的研究工作,且具有较高的成熟度[2−11].Rioboo等[2]和Okawa等[3]实验研究了液滴撞击液膜的过程,并考察了液滴撞击速度、液滴直径和液膜厚度对撞击结果的影响.研究结果表明,在不同的条件下,液滴撞击液膜后会出现3种不同的运动形态:铺展、皇冠水花和飞溅.郭加宏等[4]对液滴撞击液膜后的水花流动行为进行了可视化实验研究,发现液体黏性、表面张力、液膜厚度和液滴直径等因素均对水花流动有一定的影响.宋云超等[5]通过数值模拟对液滴撞击湿润壁面的现象进行了研究,发现随着液滴撞击速度的增大,会依次出现4种不同的运动形态:黏附铺展、波动运动、皇冠几何体运动以及飞溅运动.梁刚涛等[6]采用耦合水平集-体积分数(CLSVOF)方法数值模拟了液滴撞击液膜的运动过程,发现了液滴颈部射流的产生机理,并研究了黏度和表面张力影响水花形态转变的规律.

随着液膜厚度的增加,可以忽略壁面形貌特征对液滴撞击过程的影响.Bisighini[7]提出液滴撞击深液膜(液池)后会出现融合、弹坑状水花和飞溅3种不同的现象.Rein[8]实验研究了韦伯数(We)对聚结和飞溅现象之间的过渡过程产生影响的规律.Blanchette等[9]通过数值模拟研究了低速液滴撞击深液膜的过程,发现在某些情况下,液滴不会与液膜完全融合,而会产生一个子液滴,并将该现象称为部分融合.Chen等[10]对液滴撞击液膜中的部分融合现象进行了可视化实验,认为这些现象主要受惯性和界面张力的影响.Ray等[11]采用CLSVOF方法数值研究了液滴撞击液膜过程中由部分融合到完全融合的变化规律.

当液滴撞击液膜形成弹坑状水花时,容易形成气泡夹带现象,这一现象已引起学者们的广泛关注.在海洋和气候科学中,气泡夹带现象有利于气液界面气体进行分子交换;而在液体食品和药剂加工过程中,气泡夹带现象则会导致泡沫产生,严重影响产品质量和生产速率.由此可见,确定夹带发生的条件以及确定这种现象在数量上的发生概率是极为重要的.

相关研究显示,液滴撞击液池后会夹带大小不同的气泡[12−21].通常最小的气泡会溶解在液池内,最大的气泡会上升到自由表面并发生破裂[12].Pumphrey等[13]提出了4种气泡夹带形式:不规则夹带、规则夹带、大气泡夹带和“Mesler夹带”.其中,液滴撞击液面后形成弹坑状水花是发生规则夹带和大气泡夹带的前提.

规则夹带是指当液滴直径和速度在一定范围时,总能观察到单个气泡的夹带现象.Pumphrey等[14]对规则夹带的形成机制进行了研究,认为毛细波对夹带的形成起着至关重要的作用.Oguz等[15]考察了We数和弗劳德数(Fr)对规则夹带的影响,并以We=41.3Fr0.179和We=48.3Fr0.247作为临界曲线,在这两条曲线间的区域总能观察到规则夹带现象.

Zou等[16]和Wang等[17]对大气泡夹带现象进行了可视化实验研究,发现扁长形液滴撞击液面后能形成与液滴尺寸几乎相当的气泡.Deng等[18]研究了液体黏度和表面张力对气泡夹带的影响,发现夹带气泡尺寸随着毛细数(Ca)的增大而减小.

Thoroddsen等[19]在实验中发现低速液滴撞击液池时,液滴与液池间存在半球状的空气层阻延两者直接接触.随着时间变化,空气层发生破裂并分裂为成百上千个小气泡.Sigler和Mesler[20]较早地研究了这种现象,称其为“Mesler夹带”.Saylor和Bounds[21]通过研究发现硅油液滴比水滴更易观察到“Mesler夹带”现象.

通过上述文献可以看到,学者们主要对液滴撞击液膜的流动行为以及气泡夹带现象进行了较为系统且深入的研究,并对各现象的形成机制和不同物理参数的影响也进行了相应探讨.

在润滑系统工作过程中,油滴撞击油膜时易发生气泡夹带现象.气泡加速润滑油氧化变质,使油膜出现破裂,造成机械部件的直接接触并最终影响设备的服役寿命.此外,油滴往往是连续撞击油膜,当第一个油滴撞击油膜引起气泡夹带后,第二个油滴撞击的是含有气泡的油膜.因此,研究油滴与含气泡油膜的碰撞行为可以为润滑过程中气泡影响研究提供参考,同时对于深化气泡动力学规律的理解也具有重要意义.

当前较少见到公开发表的文献中有关于液滴与含气泡液膜碰撞行为的研究,在缺乏相关理论指导和实验研究的前提下,数值模拟研究是揭示其运动规律的有效途径.基于上述背景,本文采用CLSVOF方法模拟了油滴撞击含气泡油膜的运动过程,重点探讨油膜层中气泡在油滴撞击作用下的变化规律.

2 数值模型计算方法

2.1 控制方程

油滴撞击含气泡油膜是典型的两相流现象,气液界面流动状况十分复杂,且各物理参数间也存在较强的相互作用,求解这类问题的关键在于如何精确追踪相界面.目前,流体体积法(volume of fl uid,VOF)和水平集(level set)方法广泛应用于追踪相界面的数值模拟中.

VOF方法通过定义流体体积函数β来捕捉相界面,当β=1时,目标区域仅存在液体;当β=0时,目标区域内仅存在气体;当0＜β＜1时,目标区域为两相界面.流体体积函数β的控制方程为

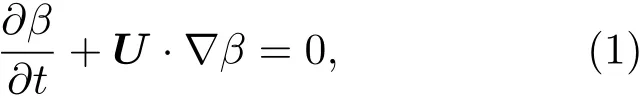
式中U为速度矢量,t为实际时间.

VOF方法在计算两相流动时能保证质量守恒,但流体体积函数β不是连续函数,不能精确计算曲率和法向向量等几何参数[22].

Level set方法通过光滑连续的水平集函数ϕ(x,t)来追踪相界面,能准确计算界面上的几何参数.通过水平集函数ϕ(x,t)可得法向向量n和界面曲率κ(ϕ)为:

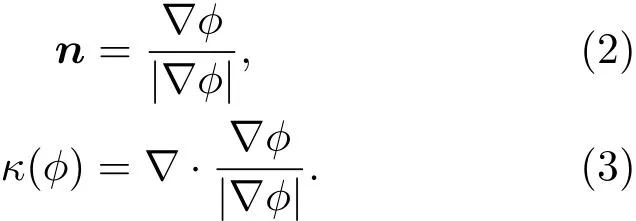
Level set方法的缺点在于求解两相流动时容易造成质量不守恒,较难追踪尖锐的界面变化.为了改善VOF和level set方法的缺陷,Sussman等[22]对这两种方法进行了耦合并提出了CLSVOF方法.

近年来,CLSVOF方法广泛应用于模拟液滴撞击壁面现象[5,6,11,23]、液体中气泡变化行为[24−26]等方面.在CLSVOF方法中,水平集函数ϕ(x,t)用来精确求解界面上的几何参数,流体体积函数β则用于计算流体体积分数.

通过CLSVOF方法可以得到气-液界面处的密度ρ(ϕ)和黏度µ(ϕ)为:

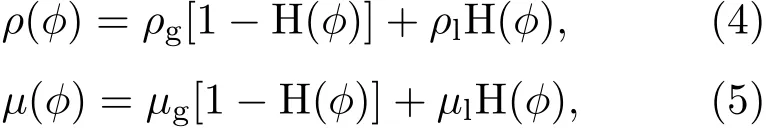
式中 H(ϕ)是Heaviside函数,下标g和l分别表示气相和液相.

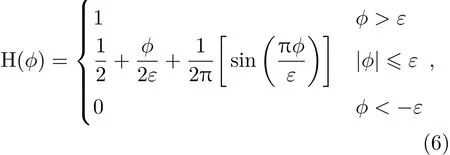
式中ε=1.5∆r,∆r为最小的网格尺寸.

表面张力的计算通过连续表面力(continuum surface force)模型[27]

来计算,式中F为表面张力,σ是表面张力系数.

两相流动的质量方程和动量方程分别表示成

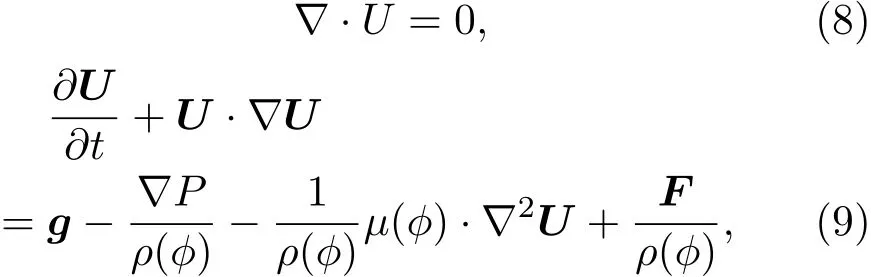
式中g为重力加速度,P为压力.

2.2 计算方法可行性验证

当前尚未见到有关液滴撞击含气泡液膜的实验研究,为验证CLSVOF方法是否能准确模拟油滴撞击含气泡油膜的变化过程,我们通过间接验证的方法对液滴撞击液膜过程中的流动行为和大气泡夹带现象进行试算.

数值计算过程中控制方程通过有限体积法进行离散,压力速度耦合采用PISO方法,压力求解使用PRESTO!方法,气-液界面插值选择几何重构方法,动量求解采用二阶迎风格式.图1(a)为扁长形液滴撞击液池后形成大气泡夹带现象的二维数值模拟结果与文献[17]中实验结果的定性对比.图中扁长形液滴的等效直径为5.65 mm,碰撞速度为0.953 m/s,We=75,Fr=16.由图1(a)可以看出,计算结果与实验观察符合较好.此外,数值计算采用二维轴对称模型,模拟结果能发现实验中无法观察的流场内部细节特征.

图1(b)为液滴撞击液膜后水花内径Din随实际时间t变化的模拟结果与文献[28]中实验结果的定量对比,其中液滴的雷诺数(Re)和We数分别为13676和667,无量纲液膜厚度δ可表示为

式中H为液膜厚度,D为液滴直径.

图1 计算结果与实验结果对比 (a)定性对比;(b)定量对比Fig.1. Comparison of experiment and simulation:(a)Qualitative comparison;(b)quantitative comparison.

从图1(b)中可以看到,撞击前期模拟和实验中水花内径Din较为接近,均随时间近似递增;但在撞击后期,模拟结果与实验结果有所差异.分析认为其原因是模拟条件与实验条件之间存在一定差异,此外,现有数字图像处理技术也存在局限性.

综上所述,CLSVOF方法既能准确捕捉液滴撞击液膜过程中的气泡形态变化,也能较精确计算出水花流动形态的特征参数变化.因此,本文采用CLSVOF方法模拟油滴撞击含气泡油膜这一动态过程.

2.3 参数选择及数值模型建立

本文以润滑油液滴作为研究对象,对油滴与含气泡油膜的碰撞行为进行研究.在不同的润滑方式中,油滴直径大小差异明显.例如,油-气润滑系统工作时,油滴颗粒直径一般为10—100µm;喷油润滑中的润滑油直径多为亚毫米级;油雾润滑中的润滑油颗粒直径约为1—3µm.为方便研究,将模拟过程中的油滴直径固定为50µm,其余相关参数如表1所列.

表1 计算时采用的相关参数Table 1.Parameters used in calculation.

图2所示为初始时刻油滴撞击含气泡油膜的二维轴对称计算域示意图.为使模拟结果具有三维特征,对二维模型的对称轴x添加轴旋转对称(axisymmetric swirl)条件.定义初始时刻油滴和油膜刚开始接触,油滴中心和气泡中心在一条直线上,气泡位于油膜高度中心.油膜底部为不滑移壁面,环境压力保持一个标准大气压.整个计算区域大小为400µm×150µm,并采用四边形网格对计算区域进行离散.

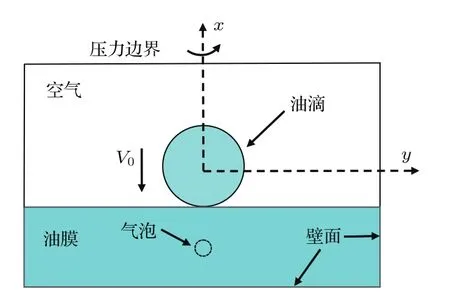
图2 计算域示意图Fig.2.Schematic of computational domain.

2.4 网格无关性分析

为验证网格的无关性,图3给出了4种不同密度的计算网格下中心油膜高度h0随实际时间t的变化情况,图中气泡直径为10µm.为提高计算效率同时保证计算精度,对气泡及周围区域网格进行局部加密,图3中网格尺寸为加密后的网格.

图3 不同网格下的中心油膜高度对比Fig.3.Comparison of central fi lm height in diff erent grids.

由图3可得,网格尺寸对中心油膜高度的变化规律有一定的影响.在30µs＜t＜45µs时,不同尺寸的网格所对应的中心油膜高度最小值所在时间不完全相同.随着网格尺寸减小,网格数量增多,气-液界面划分将越精细.从油膜高度最小值所在时间来看,当网格尺寸达到0.0332µm2时,油膜高度最小值所在时间基本不发生变化.因此,选用尺寸为0.0332µm2的网格作为计算网格.

3 结果与分析

3.1 气泡大小的影响

图4为油滴撞击含不同大小气泡的油膜时气泡的形态演化过程.图4(a)、图4(b)和图4(c)中气泡直径分别为10,20,和25µm,油滴直径固定为50µm,其余参数见表1.

由图4(a)可以看出,当运动刚刚开始时,油膜表层受油滴撞击作用有较高的竖直向下速度,油膜底层靠近壁面处速度较低,可见油膜在竖直方向上具有较大的速度梯度,具体表现为油膜内部竖直方向的黏性剪切力;而在油膜的水平方向上,油滴的部分动能转换为油膜向两侧运动的动能,使油膜内部水平方向同样存在着黏性剪切力作用.气泡在两种不同方向的黏性剪切力的共同作用下开始下沉并逐渐变为椭球形.当t=6µs时,气泡的变形程度达到最大,气泡上部较平,整体呈现半椭球形;在6µs之后,气泡受黏性剪切力的影响减弱,表面张力开始主导气泡变形;在表面张力的作用下气泡逐渐变圆,并于13µs时形成椭球形;随时间演化,当t=35µs时气泡整体形状近似于球形,且气泡上表面位置接近于液面;当t=37µs时,气泡发生破裂,位于气泡上表面的油膜受表面张力作用形成膜液滴.本文将这种运动称为“自由表面破裂”.

图4 不同大小气泡的演化过程 (a)10µm;(b)20µm;(c)25µmFig.4.Evolution process of diff erent sizes of bubbles:(a)10µm;(b)20µm;(c)25µm.

从图4(b)可以看出,当气泡直径为20µm时,油滴撞击油膜后气泡变形过程与气泡直径为10µm时基本一致,但最终气泡没有发生破裂而是稳定存在于油膜内,本文将其称为“稳定变形”.

从图4(c)可以看出,当气泡直径为25µm时,气泡变形过程出现明显变化.当t=1µs时,气泡受油滴撞击发生变形,整体类似于碗状;当t=6µs时,气泡在黏性剪切力的作用下发生破裂,并在油膜中心形成一个椭球形小气泡,小气泡外围分布着一些更小的气环,原先气泡的外侧形成一个大气环;在6µs到20µs间,油膜内的气泡和气环在表面张力的作用下逐渐变圆,油膜中心附近的气泡及气环位置几乎保持不变,边缘处的大气环随着油膜向外侧移动;在20µs到100µs间,黏滞阻力和表面张力消耗了油膜向两侧传播的动能,油膜高度开始回复,油膜中心的小气泡和周围气环发生并聚,并形成体积稍大的气泡,油膜内部外侧的大气环向油膜中心回缩;当t=200µs时,随着液面升高,两侧的大气环移动到油膜中心并形成大气泡,油膜中心的小气泡位于大气泡下方.本文将这种运动过程称为“油膜内部破裂”.

3.2 气泡大小对气泡变形特征参数的影响

由3.1节可见,气泡大小对气泡变形历程及变形特征有显著的影响.为了进一步研究气泡大小对气泡变形的影响规律,本节主要对不同直径气泡的变形特征进行分析.

为定量描述油滴撞击含气泡油膜壁面的运动特性,如图5所示,定义气泡的横向长度为w,纵向长度为h,使用无量纲化参数形状系数E来表征气泡的形状变化,并可表示为

形状系数E越大,说明气泡总体变形量越大.同样将运动变化时间以无量纲时间T表示:

式中V0为油滴的碰撞速度,t为实际时间,d0为油滴直径.

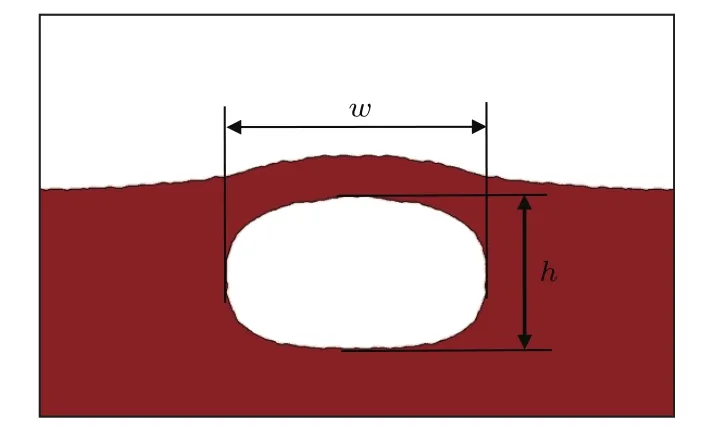
图5 气泡的横向长度w和纵向长度hFig.5.Transverse length w and longitudinal length h of the bubble.

图6 给出了气泡直径d在10—30µm条件下,油滴撞击含气泡油膜后气泡形状系数E随无量纲时间T的变化情况(为了能清晰看出差别,图中分成d 6 20µm和d>20µm两种情况,这里不列出气泡破裂后的数值变化情况).其中,油滴直径d0为50µm,碰撞速度V0为20 m/s,其余参数见表1.

图6 气泡大小对形状系数的影响 (a)d 6 20µm;(b)d>20µmFig.6.Infl uence of bubble size on shape parameter:(a)d 6 20µm;(b)d>20µm.

由图6(a)可以看出,油滴在撞击含气泡油膜后,气泡形状变化过程分为两个阶段:显著变形阶段(T<10)和相对稳定阶段(T>10).在显著变形阶段,随着气泡直径增大,同一时间的气泡形状系数也相应增大,且气泡达到形状系数最大值的时间也增加,但不明显.这是因为气泡直径越大,气泡的表面积越大,越容易受黏性剪切力拖拽而产生变形.在相对稳定阶段,各气泡间的形状系数差距较小.此外,气泡直径越大,气泡破裂发生时间越晚,且破裂前的形状系数呈现小范围波动变化.

从图6(b)中可以看出,当d>20µm时,气泡破裂发生在显著变形阶段.在T<1.8时,随着气泡直径的增大,同一时间的气泡形状系数也相应增大,但气泡形状系数最大值和气泡直径间无明的显线性关系.此外,气泡达到形状系数最大值的时间和破裂发生时间均随着气泡直径的增大而缩短.较为特殊的是,该阶段的气泡发生的是内部破裂并存在多个破裂位置,且各个位置破裂时间不完全相同.为便于分析,将气泡最先发生破裂的时间点定为破裂发生时间.经过观察发现,这一阶段的气泡破裂不是发生在气泡形状系数达到最大值时,而是发生在气泡达到形状系数最大值后的1µs内.为对这一现象进行分析,图6(b)内插图中给出了d=30µm,T=1.84和T=1.92时气泡右半空间分布相图.从内插图可以看出,在T=1.84时气泡形状系数最大,而在T=1.92时气泡靠近中心处的小范围区域内出现收缩,使气泡纵向距离h增大,引起气泡形状系数减小.随时间变化,气泡破裂发生在收缩区域内.

行为异常组在矛盾性和独立性维度的得分明显高于正常组（P＜0．05），而在亲密度、情感表达、知识性、娱乐性、道德宗教观、组织性及控制性维度的得分则明显低于正常组（P＜0．05）。见表1。

综合上述分析,气泡大小将显著影响气泡的变形历程.d=20µm是气泡两种破碎形式间的临界点,此时气泡能稳定地存在于油膜中(图6(a)仅给出了T 6 40时气泡的形状系数);当d<20µm时,气泡破碎发生在自由表面附近并处于相对稳定阶段;当d>20µm时,气泡破裂发生在油膜内部并处于显著变形阶段.

3.3 气泡位置对气泡变形特征参数的影响

3.2 节中不同大小的气泡均位于油膜中心,但各气泡顶端和油膜上表面的间距以及气泡底端和壁面的间距不相等.可见气泡大小的不同间接引起了气泡位置的变化,因此本节研究气泡位置对气泡变形过程的影响.

图7给出了d=10,20和30µm时,油滴撞击含3种不同位置(气泡顶端和油膜表面相切、气泡位于油膜中心和气泡底端和壁面相切)气泡的油膜后气泡形状系数E随无量纲时间T的变化关系.为方便说明,下文将这3个位置简称为顶端、中心和底端.此外,图7中内插图为气泡位于油膜顶端时气泡破裂相图以及气泡位于底端时气泡稳定相图,位于油膜中心的气泡变化相图可参考图5.计算过程中的其余参数见表1.

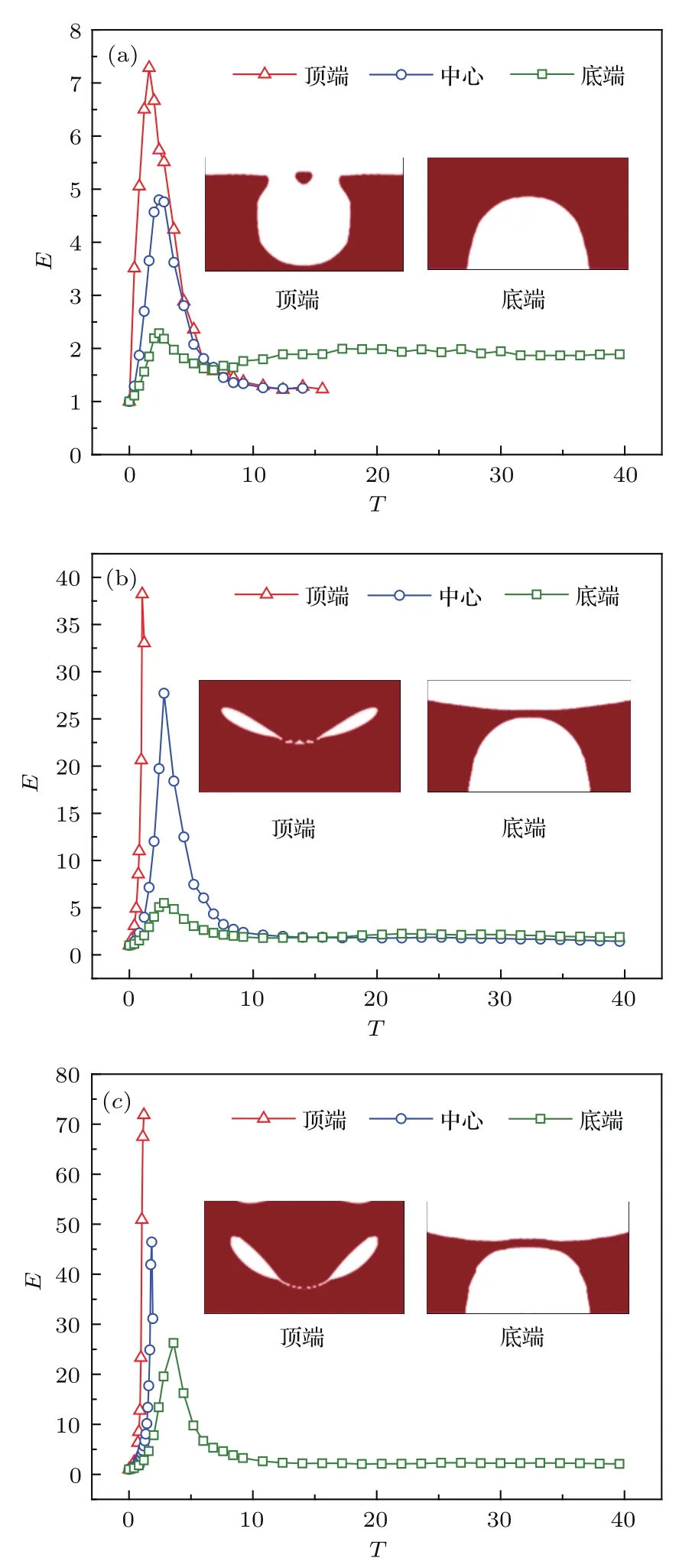
图7 气泡位置对形状系数的影响 (a)d=10µm;(b)d=20µm;(c)d=30µmFig.7.Infl uence of bubble position on shape parameter:(a)d=10µm;(b)d=20µm;(c)d=30µm.

从图7(a)可以看出,当d=10µm时,位于油膜顶端和油膜中心的气泡形状系数随无量纲时间的变化趋势保持一致,气泡均在自由表面发生破裂且破裂时间也较为接近.不同点在于T＜6时,位于油膜顶端气泡的形状系数始终大于位于油膜中心气泡的形状系数.

由图7(b)可以看出,当d=20µm时,位于油膜顶端和油膜中心的气泡形状系数随无量纲时间的变化趋势出现显著不同,其原因在于位于油膜顶端的气泡在运动过程中出现油膜内部破裂现象,而位于油膜中心的气泡在撞击过程中保持较稳定的状态.

从图7(c)可以看出,当d=30µm时,位于油膜顶端和油膜中心的气泡均在运动过程中发生油膜内部破裂现象,但油膜顶端的气泡最大形状系数远大于油膜中心的气泡最大形状系数.

图8 底层气泡大小对形状系数的影响Fig.8. Infl uence of bottom bubble size on shape parameter.

综合图7和图8中4幅图可以得出,气泡位置对气泡变形过程有一定的影响.当气泡直径相同时,气泡越接近油膜顶端受到油滴撞击的影响越强,越容易发生变形;位于油膜底端的气泡受油滴撞击影响较弱,同时壁面对气泡也有一定吸引作用,因此位于油膜底部的气泡整体变形趋势较平缓,并最终依附在壁面上维持稳定的状态.

3.4 气泡破裂机制分析

气泡破裂现象属于气泡动力学范畴.在进行气泡动力学分析时常引入两个无量纲参数,莫顿数(M o)和厄缶数(Eo):

式中g为重力加速度,µl为液体黏度,ρl为液体密度,ρg为气体密度,σ为表面张力系数,d为气泡直径.

M o数反映气泡外部液体黏性对气泡变形的影响,Eo数表征气泡浮力和表面张力的关系.Eo数越大,气泡越易受浮力作用发生形变.本文中气泡的M o=5.06,Eo=2.51×10−5—2.26×10−4,可见气泡变形过程中受液体黏性作用较大,浮力对气泡变形的影响较为微弱.

3.4.1 自由表面破裂

图9给出了气泡直径d为10µm,位于油膜中心处的气泡在破裂区域内的压力云图和速度矢量图.其中,图9(a)左侧为36.0µs时气泡分布相图,图9(a)、图9(b)和图9(c)为随时间变化的压力-速度分布图.

从图9(a)可以看出,在36.0µs时,气泡顶端已经接近油膜表面,压力最大值位于气泡上部的薄膜区域,大小为53 kPa,压力最小值位于气-液界面的两处位置,大小为−6 kPa.在图片右侧的速度分布中,油膜上方较远处的空气速度方向竖直向下,但在接近油膜层时速度方向发生变化.这是由于相互接触的空气和油膜存在相对运动,使油膜表面产生了毛细波[29].毛细波的存在使气-液界面发生不稳定现象,这正是气-液界面出现局部负压的原因.此外,气泡内表面速度方向主要受表面张力作用呈现回旋状.

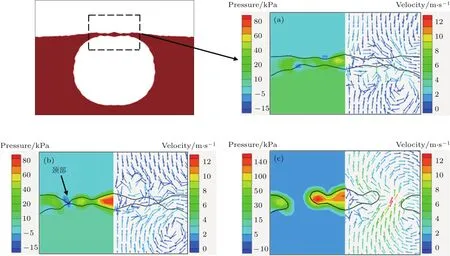
图9 气泡破裂区域压力和速度分布图(d=10µm) (a)36.0µs;(b)36.2µs;(c)36.4µsFig.9.Distribution of pressure and velocity in the region of bubble rupture(d=10µm):(a)36.0µs;(b)36.2µs;(c)36.4µs.

从图9(b)可以看出,在36.2µs时,气泡上表面的油膜形成了“颈部”区域,该区域内部压力最小值为−13.31 kPa,两侧压力为33.6 kPa.可见“颈部”区域承受较大压力梯度作用有发生断裂的趋势.由速度分布可知,受毛细波的影响,气泡上侧油膜附近速度方向变化较为剧烈.气-液相界面的曲率发生变化,造成相界面的表面张力方向发生改变并促进了“颈部”区域的形成.

从图9(c)可以看出,“颈部”区域发生断裂,气泡内部压力迅速降低,“颈部”区域内的油膜在表面张力的作用下形成膜液滴.从速度分布中可见,由于气泡发生破裂,气泡内的速度方向和大小都发生改变,气泡内的气体通过破裂口向外界逃逸,破裂口的速度最大值为11.72 m/s.

通过上述分析可知,表面张力是促使气泡破裂的主要作用力.该阶段的气泡破裂主要是由气-液界面的不稳定引起的,具体表现为毛细波传播造成油膜颈部区域压力大小和速度方向的改变.

3.4.2 油膜内部破裂

图10给出了气泡直径d为25µm,位于油膜中心处的气泡在破裂区域内的压力云图和速度矢量图.从图10(a)可以看到,在5.2µs时,气泡中心处压力为28.55 kPa,两侧压力稍小,大小为25.12 kPa.速度分布显示,气泡上侧和下侧的油膜内部速度方向竖直向下,油膜两侧速度方向呈现倾斜向下,且气泡上侧速度大于下侧速度.气泡内部速度方向由中心向两侧,两侧速度较大,为10.2 m/s;气泡中心处速度仅为2.02 m/s.可以看出,气泡内部存在较大的速度梯度,该速度梯度是气泡发生变形的主要原因.

由图10(b)可以发现,在5.5µs时,随着气泡变得扁长,气-液界面逐渐变得不稳定;气泡边界处出现负压,大小为−34.36 kPa.压力最大值位于气泡内部且偏离中心,大小为224.85 kPa.图中黑色虚线为压力梯度较大的区域,该区域内气-液界面附近的速度方向与其他区域内速度方向明显不同.此外,在红色实线内的速度局部放大图中,气泡较薄处的速度方向由水平方向转为倾斜向下,大小为1.77 m/s;气泡较厚处的速度方向仍保持水平方向,大小为11.36 m/s.

从图10(c)可以看到,在5.6µs时,气泡发生破裂,破裂位置发生在图10(b)中压力梯度较大区域.在速度局部放大图中可以发现,破裂处左边气泡的速度方向呈现两种模式:一种受外界油膜影响并与油膜速度方向保持一致;另一种是表面张力作用使气泡有变圆趋势,速度方向在气泡边缘处呈现回旋状,而破裂处右边气泡内部的速度较大并保持水平方向.可以看出,气泡破裂发生区域具有两个特征:一是气泡破裂前,该区域内存在较大的压力梯度;二是该区域位于速度方向变化的过渡范围内.

综合上述分析,这一阶段的气泡在变形过程中主要受油膜内部黏性剪切力和表面张力的作用.其中黏性剪切力作用是造成该类型气泡破裂的重要因素,具体表现为图10(a)中气泡内部较大的水平方向速度梯度,在速度梯度的作用下,气泡变得扁长.扁长形气泡的界面不稳定性使气泡内部出现较大的压力梯度,同时让气泡内部速度方向发生改变,最终破裂.

图10 气泡破碎区域压力和速度分布图(d=25µm) (a)5.2µs;(b)5.5µs;(c)5.6µsFig.10.Distribution of pressure and velocity in the region of bubble rupture(d=25µm):(a)5.2µs;(b)5.5µs;(c)5.6µs.

4 结 论

采用CLSVOF方法对油滴撞击含气泡油膜现象进行了数值模拟分析,研究了油膜层内部气泡的运动演化过程,考察了气泡大小及气泡位置等因素对受撞击作用的气泡变形特征参数的影响规律,探索了不同破裂方式下的气泡破裂机制,主要得到以下结论.

1)通过与实验结果比较,验证CLSVOF方法在求解液滴撞击液膜过程中的气泡形态变化和流动特征参数变化的可行性,并以此为依据,建立了油滴撞击含气泡油膜的数值模型.

2)气泡大小是决定油滴撞击油膜后气泡呈现自由表面破裂、稳定变形以及气泡在油膜内部破裂等不同运动形态的重要因素.

3)当10µm 6 d<20µm时,随着气泡直径增大,气泡在运动过程中的变形量也相应增大,并随时间变化发生自由表面破裂,破裂发生时间随气泡直径增大而延长;当20µm

4)当气泡位置发生改变时,气泡的变形过程也不完全相同.相同撞击条件下,位于油膜顶端的气泡比位于油膜中心处的气泡更易产生变形;位于油膜底层的气泡总体变形量最小,并最终依附在壁面上.

5)气泡发生自由表面破裂和油膜内部破裂是气-液界面的不稳定和表面张力共同作用的结果.油膜内部破裂时,除了受气-液界面不稳定性和表面张力的作用外,黏性剪切力的影响也十分重要.

[1]Peduto D 2015 Ph.D.Dissertation(Karlsruhe:Karlsruhe Institute of Technology)

[2]Rioboo R,Bauthier C,Conti J,VouéM,de Coninck J 2003 Exp.Fluids 35 648

[3]Okawa T,Shiraishi T,Mori T 2006 Exp.Fluids 41 965

[4]Guo J H,Dai S Q,Dai Q 2010 Acta Phys.Sin.59 2601(in Chinese)[郭加宏,戴世强,代钦 2010物理学报 59 2601]

[5]Song Y C,Ning Z,Sun C H,Lyu M,Yan K,Fu J 2013 Chin.J.Theor.Appl.Mech.45 833(in Chinese)[宋云超,宁智,孙春华,吕明,阎凯,付娟 2013力学学报45 833]

[6]Liang G T,Guo Y L,Shen SQ 2013 Acta Phys.Sin.62 024705(in Chinese)[梁刚涛,郭亚丽,沈胜强2013物理学报62 024705]

[7]Bisighini A 2010 Ph.D.Dissertation(Bergamo:University of Bergamo)

[8]Rein M 1996 J.Fluid Mech.306 145

[9]Blanchette F,Bigioni T P 2009 J.Fluid Mech.620 333

[10]Chen X,Mandre S,Feng J J 2006 Phys.Fluids 18 051705

[11]Ray B,Biswas G,Sharma A 2010 J.Fluid Mech.655 72

[12]Thoraval M J,Li Y,Thoroddsen S T 2016 Phys.Rev.E 93 033128

[13]Pumphrey H C,Elmore P A 1990 J.Fluid Mech.220 539

[14]Pumphrey H C,Crum L A,Bjø rnø L 1989 J.Acoust.Soc.Am.85 1518

[15]Oguz H N,Prosperetti A 1990 J.Fluid Mech.219 143

[16]Zou J,Ji C,Yuan B G,Ren Y L,Ruan X D,Fu X 2012 Phys.Fluids 24 057101

[17]Wang A B,Kuan C C,Tsai P H 2013 Phys.Fluids 25 1518

[18]Deng Q,Anilkumar A V,Wang T G 2007 J.Fluid Mech.578 119

[19]Thoroddsen S T,Thoaval M T,Takehara K,Etoh T G 2012 J.Fluid Mech.708 469

[20]Sigler J,Mesler R 1990 J.Colloid Interface Sci.134 459

[21]Saylor J R,Bounds G D 2012 AIChE J.58 3841

[22]Sussman M,Puckett E G 2000 J.Comput.Phys.162 301

[23]Guo Y L,Wei L,Liang G T,Shen S Q 2014 Int.Commun.Heat Mass.53 26

[24]Wang Z,Li Y,Huang B,Gao D M 2016 J.Mech.Sci.Technol.30 2547

[25]Ohta M,Kikuchi D,Yoshida Y,Sussman M 2011 Int.J.Multiphase Flow 37 1059

[26]Fan W,Qi T,Sun Y W,Zhu P,Chen H 2016 Chem.Eng.Technol.39 1895

[27]Brackbill J U,Kothe D B,Zemach C 1992 J.Comput.Phys.100 335

[28]Cossali G E,Marengo M,Coghe A,Zhdanov S 2004 Exp.Fluids 36 888

[29]Feonychev A I 2007 J.Eng.Phys.Thermophys.80 961