一种可控的Ioff e型冷分子表面微电阱∗

许雪艳 侯顺永 印建平

1 引 言

冷原子领域已经发展成熟并取得了令人瞩目的成就,比如原子的激光冷却[1−3]和原子玻色-爱因斯坦凝聚(Bose-Einstein condensation,BEC)[4−6]的制备等.相对而言,冷分子是近20年发展起来的新兴研究领域.从20世纪末到现在,一系列制备冷分子的技术应运而生,从缓冲气体冷却[7]到蒸发冷却[8],从静电Stark减速[9]再到激光制冷[10−16],这些方法可以制备冷分子(温度小于1 K)甚至超冷分子(温度小于1 mK).原子(或分子)阱可以囚禁冷原子(或分子),是研究冷原子(或分子)不可或缺的重要平台.囚禁于阱中的粒子(原子或分子)可应用于精密测量,这是由于在阱中可以获得更长的相互作用时间,也就是在光谱或精密测量中拥有更高的分辨率.其次,被囚禁的粒子与外界相隔离,从而可以被冷却到更低的温度,因此可应用于冷碰撞或量子简并气体的制备.国际上首个静电分子阱由Meijer等[17]于2000年通过实验证明.该静电阱是一个四极阱,即中心电场强度为零,电场强度由中心向外线性增加.随后,它们提出并验证了一种ac电阱[18],该阱既可以囚禁弱场搜寻态分子,也可以囚禁强场搜寻态分子.并且,通过选择合适电压,该电阱可以构造出四极阱、六级阱、双阱以及环形阱[19].2007年,Kleinert等[20]用一种由4个细圆环构成的静电阱实现了对超冷极性分子的囚禁.除了空间静电阱以外,芯片表面极性分子的囚禁也引起了科学家的极大兴趣.2009年,Meijer等[21,22]首次在芯片上实现了超声CO分子束的减速,并囚禁在芯片表面,2011年,Rempe等[23]通过实验验证了一种箱型的微结构电阱,该静电阱与激光相结合可以实现极性分子的Sisyphus冷却[12,24].近几年我们课题组也提出了几种用于囚禁芯片表面的静电阱[25−28].

然而,以上提到的表面静电阱和微结构阱中心电场强度均为零,分子经过势阱中心时会引起非绝热跃迁(Majorana跃迁),分子会从囚禁态转变为非囚禁态,从而引起分子的损失.原子的非绝热损失曾对国际上第一份原子BEC的制备造成了不小的麻烦.本文提出了一种Ioff e型表面微电阱,类似于Ioff e型微磁阱,电场强度处处不为零,从而有效避免了分子的非绝热损失.另外,该微电阱的中心高度和中心电场强度均可通过外场来调节,因此可用于表面量子简并气体的制备,也可以用于研究粒子与表面的相互作用、表面冷碰撞、冷化学以及精密测量等领域.

2 微电阱方案以及电场分布

本文提出的Ioff e型表面微电阱的方案如图1所示,构成电阱的电极尺寸由图中字母表示.左下角为本文所用坐标系,坐标原点与芯片表面电极的对称中心重合,x-y平面与芯片表面重合,而z轴与芯片垂直.该电阱由两对L型黄金电极构成,所有电极的厚度均为1µm,并衬与玻璃基底之上.外层一对电极宽度为a,内层电极宽度为b1和b2,内层电极间保持c1的空隙,外层电极间的空隙为c2.内外两层电极的间距为g.单个内层电极的长、宽分别为d1和d2.外层电极所加电压分别为±U1,内层电极所加电压分别为±U2,相邻的内外两个电极极性相反.

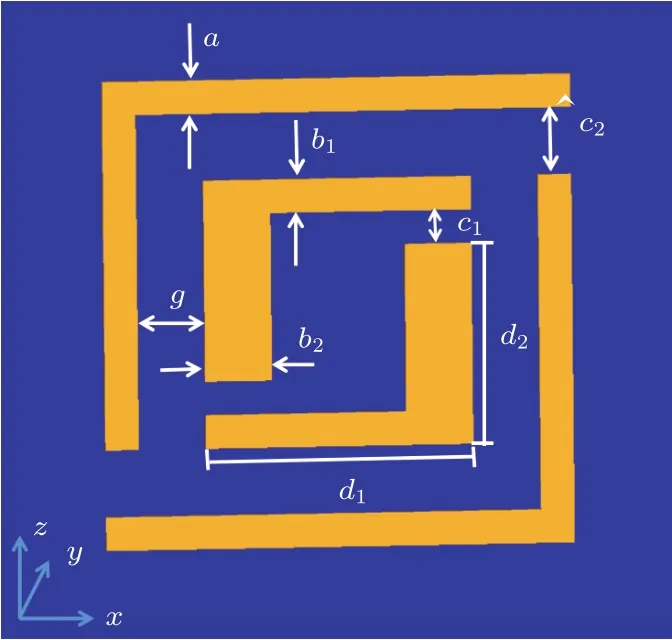
图1 芯片表面微电阱的方案示意图Fig.1.Schematic diagram of the chip-based electrostatic microtrap.

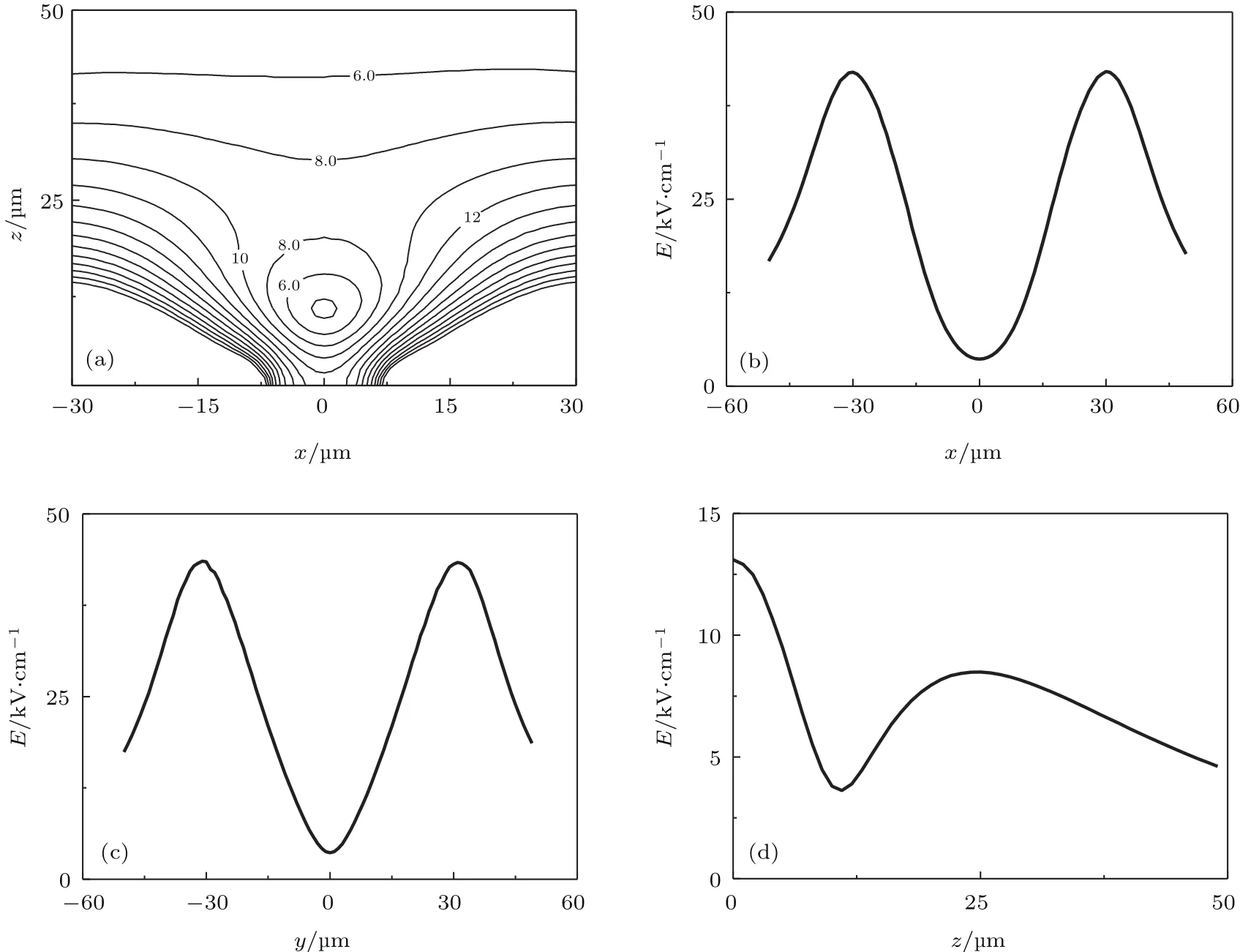
图2 (a)微电阱在x-z平面内的电场分布;(b)—(d)分别表示通过势阱中心沿x,y,z三个方向上的电场分布Fig.2.(a)Electric fi eld distribution of the electrostatic microtrap in the x-z plane;electric fi eld distribution along the lines through the minima of the potential well in x(b),y(c)and z(c)directions.

当对电极施加合适的电压,芯片表面便会形成一个封闭的三维静电阱,并且势阱中心电场不为零.该静电阱的解析解非常难得到,因此本文借助于SIMION有限元软件[29]进行计算,取如下参数:a=5 µm,b1=5 µm,b2=10 µm,c1=5 µm,c2=10µm,g=10µm,d1=40µm,d2=30µm,|U1|=150 V,|U2|=30 V.得到的电场分布如图2所示:图2(a)表示x-z平面内电场的等高线分布,由该图可以看出在该平面内可形成一个二维势阱,势阱中心距离芯片的高度约为11µm,y-z平面内的电场也有类似分布(未显示);图2(b)—(d)分别表示通过势阱中心沿x,y,z三个方向上的电场分布(E为电场强度).由此可见,在芯片表面可以形成一个用于囚禁弱场搜寻态分子的三维静电势阱,并且势阱中心电场强度不为零,可有效避免分子的非绝热跃迁.这里提到的弱场搜寻态(lowfield-seeking states)分子指的是在电场中趋向于电场减弱方向运动的分子,反之,分子则处于强场搜寻态(high-field-seeking states).下面将具体研究通过调节参数来调整势阱中心电场强度大小以及势阱中心距芯片的高度.

3 微电阱的性质

本文提出的Ioff e型表面微电阱势阱中心电场强度不为零,并且其大小可以通过调节电压或电极宽度等参数来改变.第一种方法改变内层电极电压U2.由图3(a)可以看到,当内层一对电极的电压|U2|从15 V增加到60 V时,势阱中心电场强度从4.2 kV/cm减小到2.6 kV/cm,图中实线为线性拟合结果,说明势阱中心电场强度大小与|U2|值呈线性变化.第二种方法改变内层电极的宽度b2.保持其他参数不变,仅改变内层电极的宽度b2亦可改变势阱中心电场强度的大小.由图3(b)可以看到,当|U2|=30 V时,b2从5.0µm增加到15.0µm,势阱中心电场强度相应由0.15 kV/cm逐步增加到5.1 kV/cm,图3中实线是二次函数拟合结果.如果同时改变电压|U2|和宽度b2,势阱中心电场强度可以在更大范围内变化.例如:当b2=15µm,|U2|=15 V,势阱中心电场强度为5.5 kV/cm.

另外势阱中心距芯片表面的高度h也可通过调节|U2|进行改变.从图4可以看到,当电压|U2|从15 V增加到60 V时,势阱高度则由6.0µm增加到17.0µm.

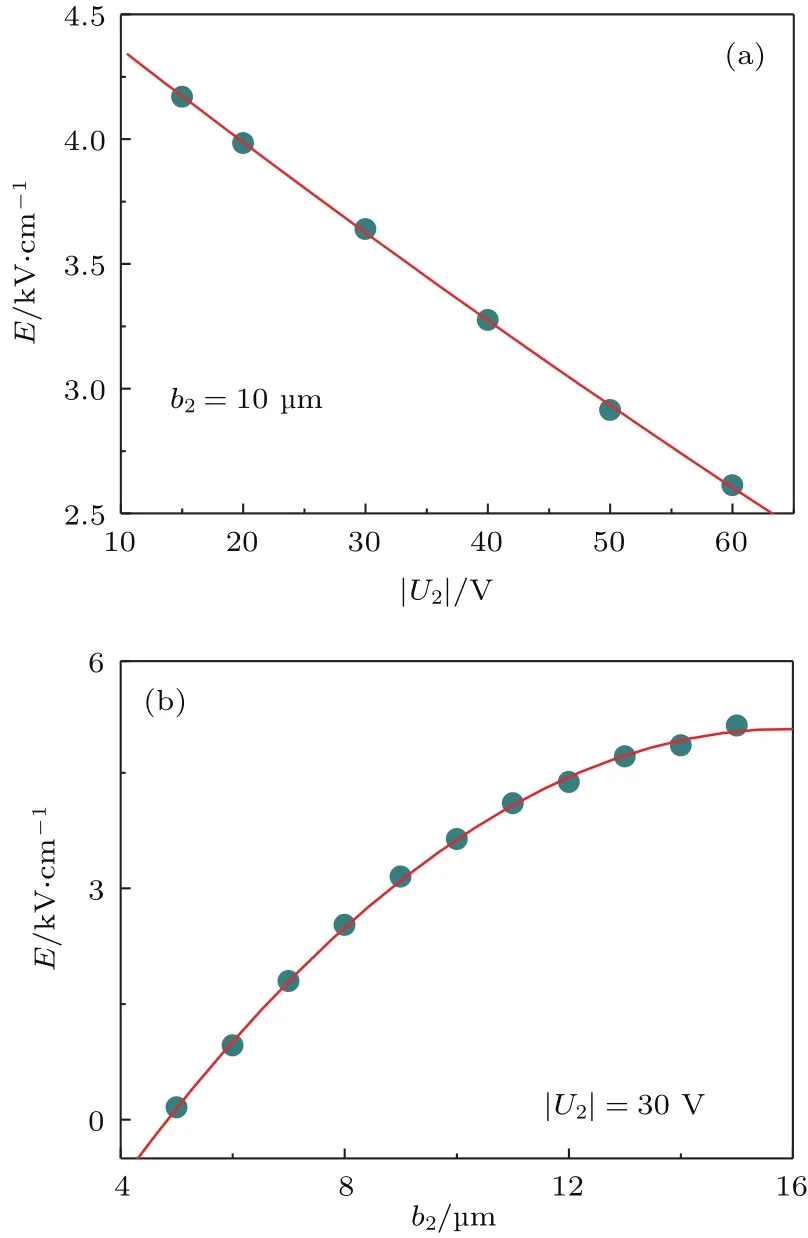
图3 势阱中心电场强度与电压|U2|(a)和电极宽度b2(b)的关系Fig.3.Electric fi eld strength at the center of the potential well as a function of|U2|(a)and b2(b).

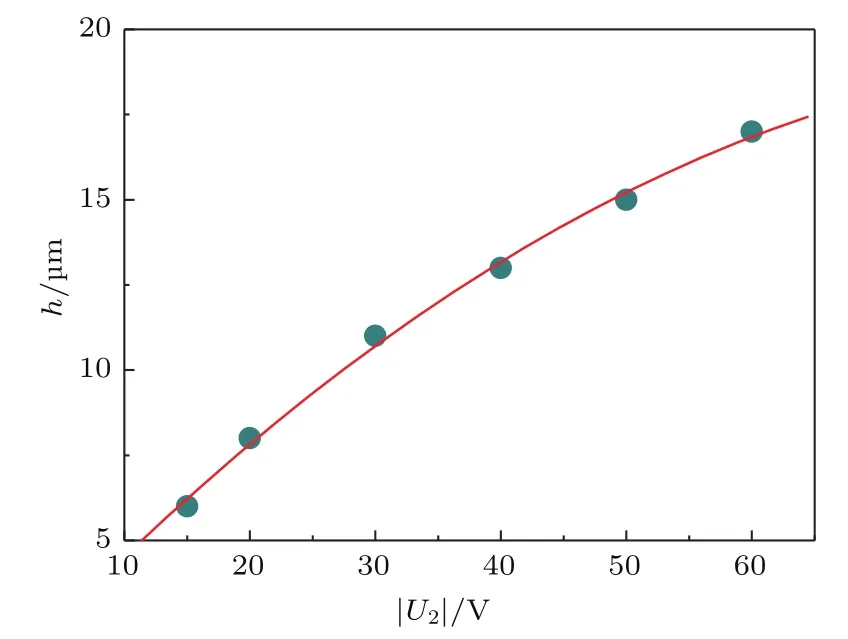
图4 势阱中心距芯片表面高度h与电压|U2|的关系Fig.4.Height of the center of the potential well h as a function of|U2|.

4 极性分子的装载与囚禁过程

4.1 极性分子与电场的相互作用

电荷分布的不对称导致极性分子拥有电偶极矩,电偶极矩与电场的相互作用被称为Stark效应.处于电场中的极性分子受到的外部电场力为

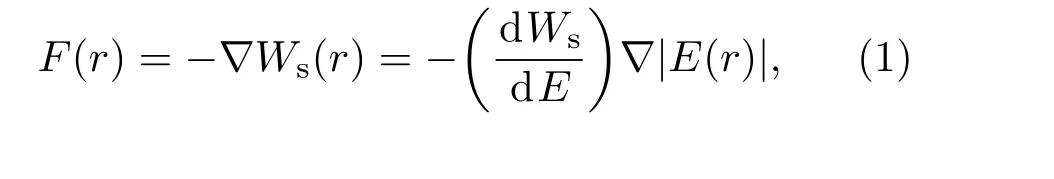
其中Ws为分子的Stark势能;可以看作是分子的有效电偶极矩µeff;分子的受力方向与分子所处的量子态有关.对于重氨分子,施加电场以后J=1,K=1态的对称与反对称能级互相排斥而分裂成4个能级,ND3分子低转动态的Stark分裂如图5所示(J为总角动量,K为J在分子轴上的投影,M为J在外场方向上的投影).当电场强度小于100 kV/cm,不同J能级之间的相互作用可以忽略,其Stark势能可以近似为

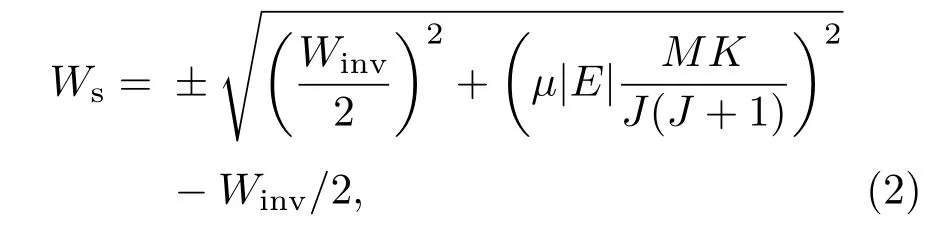
其中Winv为零场下分子的反演分裂,µ为分子的电偶极矩.

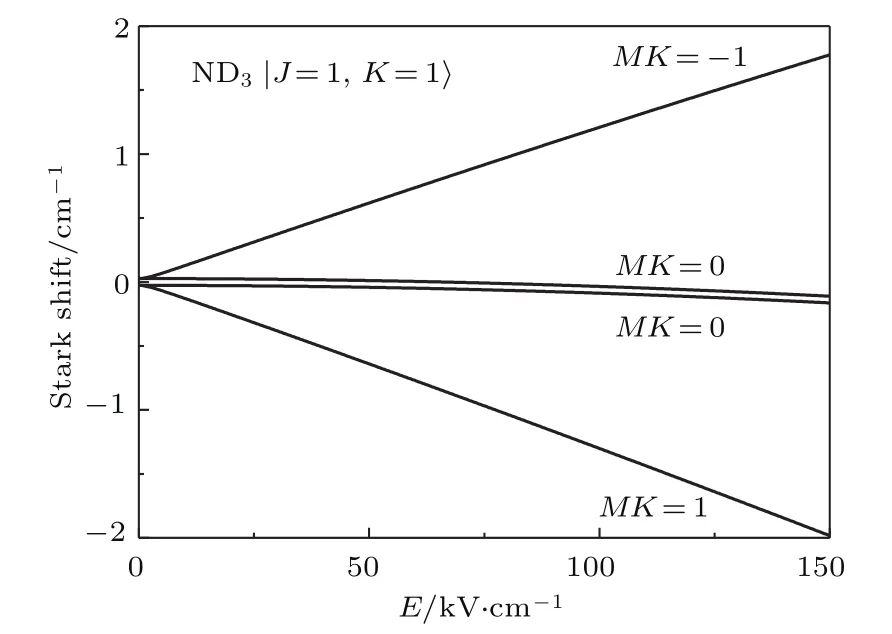
图5 ND 3分子的Stark效应Fig.5.Stark eff ect of ND 3 molecule.

4.2 M onte Carlo模拟

为了验证本文提出的表面微阱的可行性,采用Monte Carlo模拟计算了极性分子的装载与囚禁过程.选取处于|J,K M⟩=|1,−1⟩态的ND3作为验证分子,该分子样品可以通过静电Stark减速方法从超声束获得[30,31].从Stark减速器末端获得的冷分子样品沿z轴飞向微电阱.模拟计算中分子束初始的空间和速度分布均为高斯分布,分子束在x,y,z三个方向上空间与速度的分布宽度分别为[50µm×3.0 m/s]× [50µm×3.0 m/s]×[200µm×4.0 m/s],此处分布宽度指的是半高全宽(FWHM).分子束初始的空间和速度中心分布为y=0,vy=0,x=0,vx=0,z=1.0 mm,vz=10 m/s.分子束的初始分子数目为500万个.施加电场电压U1=150 V,U2=30 V.在模拟中,背景气体与ND3分子碰撞造成的损失以及芯片表面热辐射忽略不计,这是由于目前的真空技术和冷却技术可以大幅减少这些损失[32].非绝热跃迁造成的分子损失也没有考虑,这是由于本文的势阱中心电场强度不为零,可以有效避免该损失.分子受到的电场力由(1)式和(2)式得到.通过精确的时序控制来操控施加在电阱电极上的电压,可以将冷分子样品的纵向中心速度减为零,然后将其囚禁在势阱中心附近.模拟计算从距离芯片表面1.0 mm处开始,分子样品沿z轴向芯片飞行,如图6(a)所示.分子飞行到芯片表面附近时会感受到微电阱的电场力,因而样品的中心速度逐步降低,在芯片表面约24µm(图6(a)A点)的地方突然关掉电场,让分子在空间自由飞行至B点.然后打开电场,分子样品会感受到电场力,分子样品中心速度进一步减速到零(图6(a)C点).最终分子被囚禁在微电阱中.图6(b)为Monte Carlo模拟计算得到的不同电压下ND3分子装载效率η与分子纵向中心速度的函数关系,图中数值为模拟时的电极电压,数据点为模拟计算结果,实线为拟合结果.这里装载效率定义为被微电阱囚禁的分子数与初始总分子数之比.单从每一组数据来看,分子的装载效率依赖于入射分子束的中心速度,每个电压下都有一个最高装载效率.另外,从图6(b)三组数据可以看出装载效率随着电压的升高而升高.图6(c)为分子在z方向的相空间分布.由模拟结果可以得到被囚禁分子样品的温度,这里温度T的定义由公式(3/2)kBT=(1/2)kBTL+kBTT[33]给出(kB为玻尔兹曼常数,TL和 TT分别为分子样品的纵向和横向温度),分子样品各方向上的温度由Tx,y,z=m∆v2x,y,z/8ln 2·kB[34]给出(m为分子质量,∆vx,y,z为速度分布宽度).从模拟结果得到分子样品的温度约为30 mK.图6(d)为阱中ND3的分子密度与囚禁时间的依赖关系,插图是ND3分子在z方向的振荡情况,红色实线是拟合结果,根据拟合得到该方向上的振荡频率约为fz=254 kHz.对于ND3分子,势阱中心附近(±5µm)是一个谐振阱,并且大部分分子集中在这个区域.z方向势能可以表示为Uz=kz·z2/2,其中kz=mω2z,ω为振荡频率.从本文计算的电场强度可以导出z方向ND3的势能分布,由此得到fz=ωz/(2π)=249 kHz,这与模拟得到的频率相符合.通过以上计算可以证明本文提出的表面微电阱可以有效装载并囚禁极性冷分子,验证了本文方案的可行性.

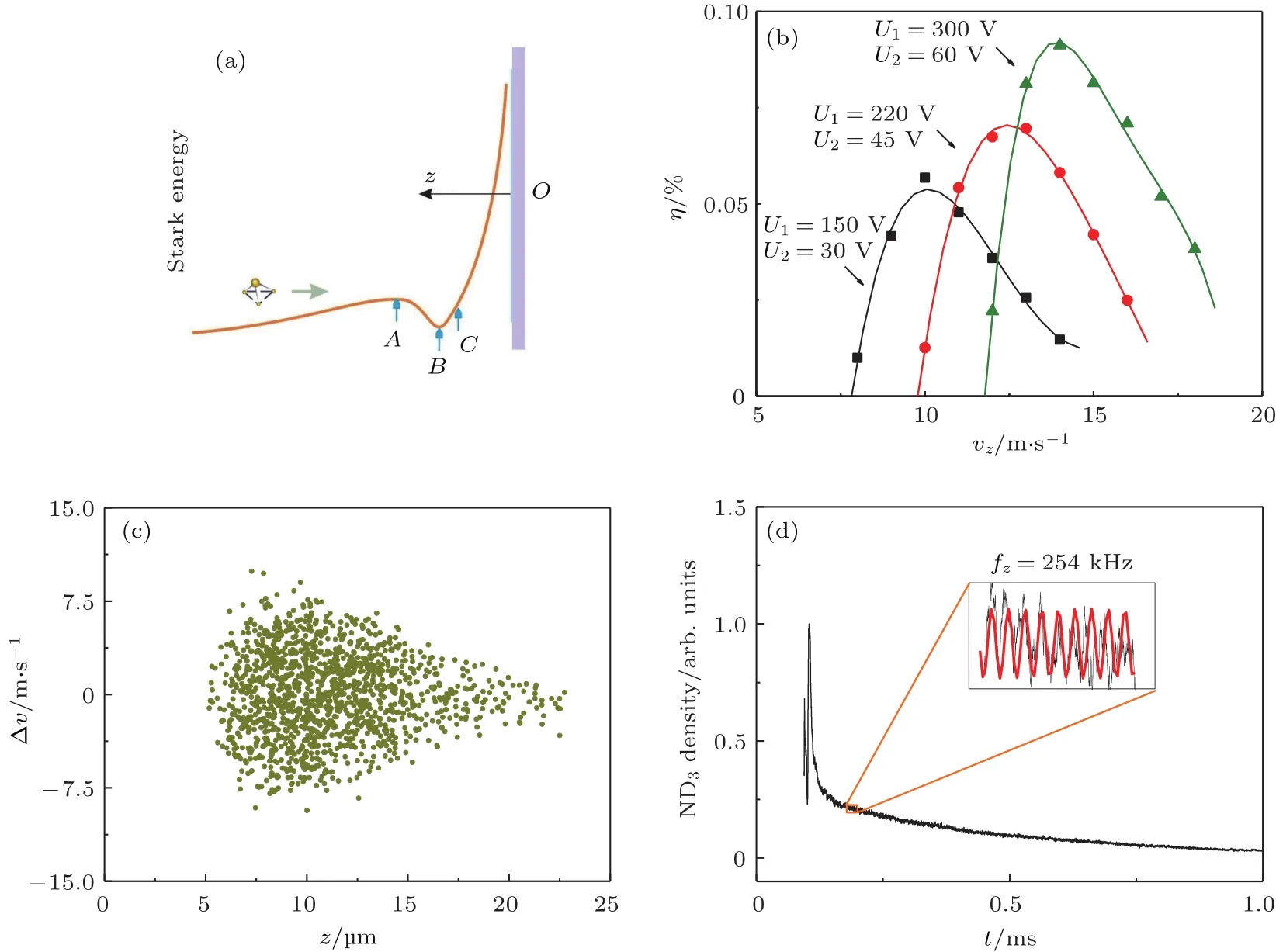
图6 (a)ND 3分子装载过程图;(b)Monte Carlo模拟计算得到的不同电压下ND3分子装载效率η与分子纵向中心的函数关系;(c)模拟计算得到的ND 3分子在z方向的相空间分布;(d)阱中ND3的分子密度与囚禁时间的依赖关系Fig.6.(a)Loading process of cold ND 3 molecules into the microtrap;(b)loading effi ciencyηof ND 3 molecules at diff erent voltages as a function of the center velocity of the molecular packets,resulted from Monte Carlo simulations;(c)phase space distribution of ND 3 in the z directions;(d)dependence of the molecular density of the ND 3 sample in the trap on the trapping time.

5 结 论

本文提出了一种势阱中心不为零的Ioff e型表面微电阱.该微电阱由两对L型黄金电极构成,结构紧凑、稳定.电极尺度在70µm左右,厚度为1µm,施加电压在100 V量级.该表面微电阱的电场处处不为零,且势阱的中心高度和电场强度大小均可调节.通过调整电极宽度和电极电压,势阱中心的电场强度大小可以在0.15—5.5 kV/cm大范围调节.势阱中心的高度也可以通过电压调节在6.0—17.0µm变化.

该微电阱电场处处不为零,故可避免分子非绝热跃迁造成的损失,因此可广泛应用于分子的绝热冷却、Sisyphus冷却、蒸发冷却,乃至量子简并气体的制备.如果将这些静电阱排成二维阵列可以制备二维超冷极性分子样品,这些超冷极性分子可以作为量子比特[35−39]应用于量子计算.另外,本文势阱中心高度和大小均可调节,因此可应用于分子与表面的相互作用研究.该表面微电阱具有的特性和优势不仅使其可用于分子芯片的集成、超冷分子的制备,而且为精密测量、量子计算、表面冷碰撞和冷化学等领域的研究提供了一种新的有效手段.

[1]Chu S 1998 Rev.Mod.Phys.70 685

[2]Cohen-Tannoudji C N 1998 Rev.Mod.Phys.70 707

[3]Phillips W D 1998 Rev.Mod.Phys.70 721

[4]Anderson M H,Ensher J R,Matthews M R,Wieman C E,Cornell E A 1995 Science 269 198

[5]Bradley C C,Sackett C A,Tollett J J,Hulet R G 1995 Phys.Rev.Lett.75 1687

[6]Davis K B,Mewes M O,Andrews M R,van Druten N J,Durfee D S,Kurn D M,Ketterle W 1995 Phys.Rev.Lett.75 3969

[7]Weinstein J D,de Carvalho R,Guillet T,Friedrich B,Doyle J M 1998 Nature 395 148

[8]Stuhl B K,Hummon M T,Yeo M,Quéméner G,Bohn J L,Ye J 2012 Nature 492 396

[9]Bethlem H L,Berden G,Meijer G 1999 Phys.Rev.Lett.83 1558

[10]Shuman E S,Barry J F,Glenn D R,DeMille D 2009 Phys.Rev.Lett.103 223001

[11]Shuman E S,Barry J F,DeMille D 2010 Nature 467 820[12]Zeppenfeld M,Englert B G U,Glöckner R,Prehn A,Mielenz M,Sommer C,van Buuren L D,Motsch M,Rempe G 2012 Nature 491 570

[13]Hummon M T,Yeo M,Stuhl B K,Collopy A L,Xia Y,Ye J 2013 Phys.Rev.Lett.110 143001

[14]Zhelyazkova V,Cournol A,Wall T E,Matsushima A,Hudson J J,Hinds E A,Tarbutt M R,Sauer B E 2014 Phys.Rev.A 89 053416

[15]Barry J F,McCarron D J,Norrgard E B,Steinecker M H,DeMille D 2014 Nature 512 286

[16]Kozyryev I,Baum L,Matsuda K,Hemmerling B,Doyle J M 2016 J.Phys.B:At.Mol.Opt.Phys.49 134002

[17]Bethlem H L,Berden G,Crompvoets F M H,Jongma R T,van Roij A J A,Meijer G 2000 Nature 406 491

[18]van Veldhoven J,Bethlem H L,Meijier G 2005 Phys.Rev.Lett.94 083001

[19]van Veldhoven J,Bethlem H L,Schnell M,Meijer G 2006 Phys.Rev.A 73 063408

[20]Kleinert J,Haimberger C,Zabawa P J,Bigelow N P 2007 Phys.Rev.Lett.99 143002

[21]Meek SA,Bethlem H L,Conrad H,Meijer G 2008 Phys.Rev.Lett.100 153003

[22]Meek S A,Conrad H,Meijer G 2009 Science 324 1699

[23]Englert B G U,Mielenz M,Sommer C,Bayerl J,Motsch M,Pinkse P W H,Rempe G,Zeppenfeld M 2011 Phys.Rev.Lett.107 263003

[24]Prehn A,Ibrügger M,Glöckner R,Rempe G,Zeppenfeld M 2016 Phys.Rev.Lett.116 063005

[25]Li S Q,Xu L,Xia Y,Wang H L,Yin J P 2014 Chin.Phys.B 23 123701

[26]Wang Q,Li S Q,Hou S Y,Wang H L,Yin J P 2014 Chin.Phys.B 23 013701

[27]Ma H,Zhou P,Liao B,Yin J P 2007 Chin.Phys.Lett.24 1228

[28]Ma H,Xu X Y,Yin J P 2011 Acta Opt.Sin.31 16(in Chinese)[马慧,许雪艳,印建平 2011光学学报 31 16]

[29]http://simion com/[2018-1-27]

[30]Hou S Y,Li S Q,Deng L Z,Yin J P 2013 J.Phys.B:At.Mol.Opt.Phys.46 045301

[31]Bethlem H L,Crompvoets F M H,Jongma R T,van de Meerakker S Y T,Meijer G 2002 Phys.Rev.A 65 053416

[32]Buhmann S Y,Tarbutt M R,Scheel S,Hinds E A 2008 Phys.Rev.A 78 052901

[33]Scoles G,Bassi D,Buck U,Laine D,Braun C 1986 Atomic and Molecular Beam Methods(New York:Oxford University Press)p27

[34]Gupta M,Herschbach D 1999 J.Phys.Chem.A 103 10670

[35]DeMille D 2002 Phys.Rev.Lett.88 067901

[36]Yelin SF,Kirby K,CôtéR 2006 Phys.Rev.A 74 050301

[37]AndréA,Demille D,Doyle J M,Lukin M D,Maxwell S E,Rabl P,Schoelkopf R J,Zoller P 2006 Nat.Phys.2 636

[38]Kuznetsova E,CôtéR,Kirby K,Yelin S F 2008 Phys.Rev.A 78 012313

[39]Rabl P,DeMille D,Doyle J M,Lukin M D,Schoelkopf R J,Zoller P 2006 Phys.Rev.Lett.97 033003